引领“再认识”，让学习在认识的优化与深化中走向深刻——以《三角形面积计算的再认识》教学为例

文|管小冬

“再认识”指“对已进行认识的认识对象及其认识成果（包括获取这些认识成果的认识活动）的重新认识”。相比于原有认识，再认识是“认识连续地和不断地深化和更新的过程”。在小学数学的学习中，受年龄、生活经验、认知水平等影响，学生对一些重要的数学内容、方法、思想的理解和掌握，往往需要经历“认识、实践、再认识、再实践”的循环递进过程。基于此，《数学课程标准（2011年版）》特别指出：在教材编写时，“重要的数学概念与数学思想要体现螺旋上升的原则”。这也要求我们，不仅要在学生初次认识这些重要的数学内容、方法、思想时上好“种子课”，更要在后续学习中精心设计问题、创设机会，上好拓展课与整合课，引领学生在对相应内容的“再认识”中实现认识的优化与深化，让学习不断走向深刻。

事实上，无论是《数学课程标准（2011年版）》对各学段“内容标准”的具体规定，还是各版本数学教材的具体编排，均十分注重使学生在“认识”“再认识”的过程中不断加深对数学知识与技能背后的数学本质的理解。比如，苏教版教材对“分数的认识”这一内容的编排，就分为三个阶段：三年级上册“分数的初步认识（一）”，三年级下册“分数的初步认识（二）”，五年级下册“分数的意义和性质”。再如，对“三角形的内角和”这一具体内容的编排，苏教版教材在例题后的练习中，就出现了如下图题目。究其用意，正是为学生提供一个新的观察与推理的视角，引导他们于“再认识”中达成对“三角形的内角和是180°”的深刻理解，对相应的观察、探究、推理方式的深刻把握。

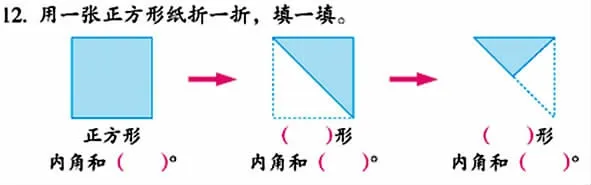
但我们仍应看到，教学中，我们对“再认识”的重视与研究还是不够。

一方面，教材的编排，我们的教学，需要引领学生通过一节课、一个单元或几个单元的学习，去掌握人类历经几百甚至几千年探索得出的数学成果。因此，教材在编排时，往往呈现的都是这些数学成果的最高形式，并为学生设计了一条易于认识与理解的便捷、高效之路。教学中，如果教师只是将这些数学成果看作是静态的数学知识与技能，未能引导学生于“认识”“再认识”的过程中充分经历联系、反思、优化等思维过程，学生的学习便会落入简单化的境地。比如，在竖式除法的教学中，教师往往注重引导学生理解竖式除法的算理与算法，却忽视了在此基础上学生对竖式除法的再认识。即，我们不应仅满足于学生对竖式除法的工具性掌握，还应引领他们回归原点，在立足除法意义的基础上，联系加、减、乘等运算，去思考、理解运用竖式除法寻找答案的运算过程，形成对竖式除法算理及运算形式、程序的“再认识”。

另一方面，教学中，特别是在新课学习之后，虽然教材、教师均注重通过不同形式的练习去巩固、发展学生对相应数学内容的认识，但练习的目标往往指向于学生对相应数学知识、技能的熟练运用，而忽视了应采取不同方式去促进学生认识的广度与深度的提升。即，教学应立足“认识具有不断反复和无限发展的规律”这一特点，着力引导学生于“再认识”中不断更新认识，进而带动他们对相应数学内容的理解走向新的境界。郑毓信教授特别强调“教学应当帮助学生学会‘长时间思考’”，也正是因为“长时间思考”可以带动学生对自身学习过程与学习结果的反思与再认识，进而使学习从“由薄到厚”走向“由厚到薄”。

接下来，我将以“三角形面积计算的再认识”教学为例，与大家分享我的思考与实践。

【案例】“三角形面积计算的再认识”

在学生学习“三角形的面积计算”后，我们会发现，总有些学生在后续遇到与三角形面积计算相关的实际问题时，会将三角形的面积计算方法与平行四边形的面积计算方法相混淆，在“底×高”后会忘记“除以2”。针对这样的“顽症”，教师们也是煞费苦心，比如“要求学生熟记、背诵三角形的面积计算公式”“在解决问题时，看到‘三角形’就在旁边标上‘÷2’”等。但实际运用中，这些方法收效甚微。访谈中我们也会发现，这些学生并不是不知道三角形的面积计算方法，在出错后也能快速地找到自己的错因，但在实际运用时就是容易忘记。通过对既往教与学过程的深层次剖析，我发现原因主要源自两个方面。

一是在看似快速、高效的学习过程中，学生掌握了三角形的面积计算方法，但因为缺乏对“提出初始想法、试误、反思、调整、形成最优化表达”这些关键环节的深刻经历，学生也只是掌握了方法，并未形成对方法的深刻理解。关于这一点的解决之法，大家可以参考本刊2021年第6 期《注重“真体验”，让学习在关键环节的真实经历中走向深刻》一文，此处不再赘述。

二是学生对三角形面积计算公式中的“÷2”缺乏更深层次的认识与理解。“用两个完全一样的三角形拼成一个平行四边形，再由平行四边形的面积计算公式推导出三角形的面积计算公式”，这几乎是公认的最易于为学生理解、掌握的教学之道。但实际上，由于初始想法可能不同，过程中的思路也可能迥异，三角形面积计算的推导过程就会千差万别。如果缺少了对这些不同思路与推导过程的比较、联系、梳理与归纳，学生是很难深刻理解上述“公认”推导过程的优越性所在的，更不会真正认识到：公式中的“÷2”不仅代表着“三角形的面积是与它等底等高的平行四边形面积的一半”，更代表着“转化”这一重要的数学思想。如此，“公认”也就只是教师（成人）自认为的、基于“儿童立场”出发的“公认”了。

基于以上分析与思考，在“三角形的面积”一课教学后，我布置了一项“长期作业”给学生，请他们继续思考、探究“三角形的面积还可以怎样算”，并在一至两周后引领他们在相互交流、对比的基础上，形成对三角形面积计算方法的“再认识”。以下是课堂教学中的两则片断。

片断1：三角形面积计算的再探究与再交流。

师：这段时间，大家都在研究“三角形的面积还可以怎样算”，有收获吗？今天这节课，我们就一起来交流大家找到的“另类”计算方法。

生：我的方法还是继续把三角形转化为平行四边形，但转化的方式与前面学过的不同。大家看（边说边操作），把这个三角形沿平行于底的这条线对折，再把上面的小三角形剪下来，与下面的梯形拼成一个平行四边形。这个平行四边形的底就是三角形的底，高是三角形高的一半。所以三角形的面积可以用底（a）乘高（h）的一半来算，也就是“SΔ=a×（h÷2）”。

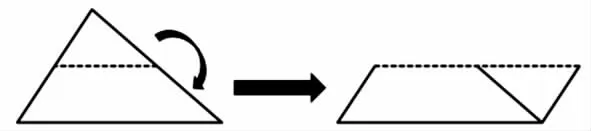
生：你这个方法可以叫做“正广以乘半从”。我进一步研究了数学书“你知道吗？”中介绍的“半广以乘正从”的方法。它是以三角形的一条边为底，从另外两条边的中点向这条边作垂线段，形成两个小的直角三角形，把这两个直角三角形剪下，再拼到上面，三角形就转化成了长方形。这时，长方形的长就是三角形底（a）的一半，即书上说的“半广”，宽就是三角形的高（h），也就是“正从”。所以，三角形的面积计算方法就是“半广以乘正从”，写成公式就是“SΔ=（a÷2）×h”。

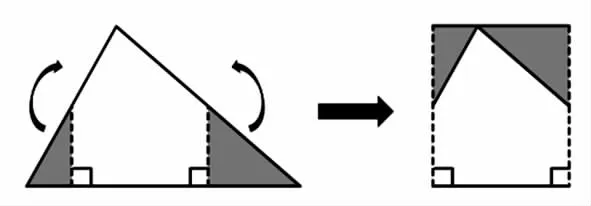
生：我的方法与你们俩的有些相似，但我没有剪拼，而是像以前研究三角形内角和那样，把左右两个直角三角形向内折，把上面这个小三角形向下折，就形成了一个长方形。但是大家注意，这其实是两个长方形。这个长方形的长是三角形底的一半，宽是三角形高的一半。所以三角形的面积可以用它底（a）的一半乘高（h）的一半，再乘以2 来计算，也就是“SΔ=（a÷2）×（h÷2）×2”。借用“你知道吗？”中的说法，可以称为“2 倍的半广以乘半从”。

……

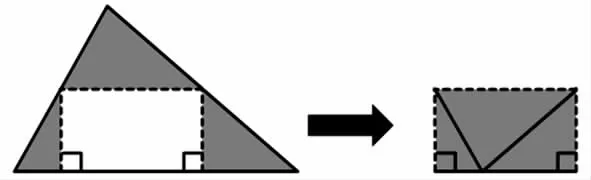
“三角形的面积还可以怎样算？”这项“长期作业”的布置，并不是要学生穷尽三角形面积计算的推导方法（事实上也不可能），而是意在引导学生对一问题进行“长时间思考”，进而在这一过程中不断体会图形间的相互转化与联系，获得数学活动经验的积累、推理能力的提升以及数学思考的发展。上述片断中，学生间不同推导方法的交流，既是对三角形面积计算方法的丰富与补充，也为后续的“再梳理”与“再认识”提供了足够广远的思考和理解的空间。

片断2：三角形面积计算方法的再梳理与再认识。

师：刚才的交流真是精彩纷呈。原来三角形的面积计算还可以有如此多的“另类”方法。不过，我们对数学的研究，不能仅止步于各种具体方法的获得，还要学会对比与联系。想一想，这些不同的方法之间有联系吗？它们的异同点是什么？

学生先独立观察、对比与思考，再在小组内进行交流。随后教师组织全班交流。

生：这几种方法都是把三角形转化成平行四边形或长方形，再去研究它的面积计算方法。

师：对，“化未知为已知”是我们在数学研究中常用的一种重要方法。

生：区别就在于，转化前后，有些是面积不变，但底或高中总有一个变成了原来的一半；有些是底和高虽然是原来的一半，但三角形的面积是转化后图形面积的两倍。

生：我发现，第三种方法“SΔ=（a÷2）×（h÷2）×2”中，后面的“×2”可以与前面的一个“÷2”抵消。这样，不管是哪种方法，三角形的面积计算方法最终都可以表示为“底×高÷2”。

师：看来，“÷2”在三角形的面积计算中有着重要的意义。放在不同的位置，就对应着大家找到的不同的计算思路。不过，这么多方法中，你觉得哪种方法最易为大家理解和掌握？

生：应该还是书上例题中介绍的方法，因为相比其他几种方法，我们更容易根据它的推导图想到对应的计算方法，根据计算方法也更容易联想到对应的推导图。

至此，经过对三角形面积计算不同方法的再梳理与再认识，学生会发现“不同方法却殊途同归”。对他们而言，三角形的面积计算方法，特别是其中的“÷2”，就不再是一个需要去记忆、背诵的单纯知识点，而是不同思路经由数学化后的一致表达。在这样的“再认识”后，学生对“三角形的面积计算”才是“彻底懂，经过消化的懂”。因为，教学留给学生的不再仅仅是一条简单的面积公式，一种静态的方法、技能，而是一个生动活泼的、具备多种表征方式的数学话语体系。

陈省身先生说：“天下美妙的事不多，数学就是这样美妙的事之一。”我想，“数学好玩”正是因为在持续深入的“认识”与“再认识”中，总会有一些新的思考与发现产生。而教师的作用，正在于引领学生在“认识”“再认识”的反复中“由薄变厚”再“由厚变薄”，进而让学习在认识的不断优化与深化中走向深刻。