架构课程期待与学生学习之间的桥梁——浙教版《市场里的数》单元整合实践与反思

文|陈敏 边 聪 王俊

为了方便研究，“QUASAR”区分出课程任务发展的不同阶段，分别为“期望的课程”“实施的课程”和“实现的课程”。“期望的课程”指教学大纲中规定、教材编写中预设的课程；“实现的课程”是指最终学生实际的学习收获。从期望的课程到实现的课程，转化的关键在于实施的课程：即由教师主导的、在课堂中实际发生的教学过程。

数学任务框架

图1 数学任务在课堂教学中的展开过程示意图

“单元整合”是当下的一个热点议题。如果用上述框架来理解单元整合的问题，我们认为：教师所做的单元整合，仍属于“实施的课程”范畴。即，教师做单元整合的根本目的不是要创编一套新的学习材料（“期望的课程”），而主要是如何利用好现有的学习材料（即教材），比照本班学生的学习实际，做针对性的增补、删减、重构，以促进学生的学习，更好地实现课程预设的目标。简单地说，是对教材的“班本化”“师本化”。

我们按以下三个步骤开展单元整合设计：第一，分析教材设定的单元目标及预设的学习路径；第二，结合经验和实测，明确本班学生的认知基础和潜能、偏好；第三，对比前两点，发现期望课程与学生实际学习能力之间的差异和距离，进行整体的单元整合和个别的环节重构。

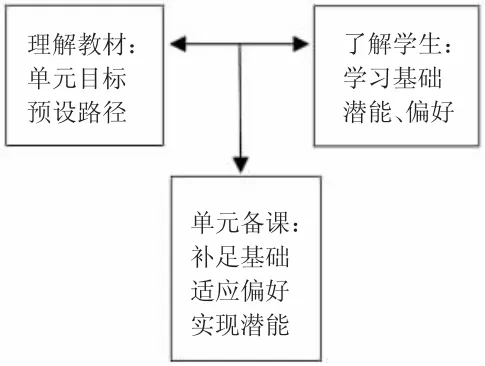
图2 单元整合流程示意图

下面以浙教版一年级下册第三单元《市场里的数》为例，作具体阐述。

一、教材分析

1.单元内容分析。

浙教版教材是国家审定的、适合部分较发达地区（学校）使用的实验教材，在学习内容组织方面独具特色。

图3 浙教版一年级下册第三单元目录

认真审读本单元的目录，可以发现，前三课均围绕数的意义：第一课时聚焦计数单位的认识；第二课时主要是对百以内数的单位构成进行分析，从基数角度理解数的意义；第三课时通过寻找“百数表”规律的活动，引导学生感知数序，从序数角度进一步体会十进计数结构、数与数之间的关系，完善数的概念。后三课则可以理解为数的概念在不同问题情境中的应用，具体包括：数的大小比较（单位大小比较或同单位个数比较）、不进位加（单位累计或继续数数）、不退位减（单位消减或倒数）。从而，可概括出教材预设的本单元目标是围绕“单位”的概念，在灵活多变的情境中，建构和理解数的意义。教材预设路线是：先“明理”后“应用”，是一种演绎的路径。

2.知识点序列分析。

好的教材往往具有知识内容螺旋上升的编排特点。我们进一步寻找与本单元直接相关的基础内容和发展章节。结果发现：在整数的认识这个序列上，本单元之前，教材已安排有“10 与几”（一年级上册）、“40以内数的认识”（一年级下册）。即，从教材逻辑讲，本课之前，学生已经具有两位数单位意义的分析经验（只不过数的大小在40 以内而已）。

而本单元之后，学生还将继续认识“三位数、四位数的读写”（二年级下册），“十进制计数法”和“万以上数的读写”（四年级下册）。关键仍在计数“单位”的概念。任何一个数的意义都可分析为两层：（1）以什么单位计数？（2）有几个这样的计数单位？（有时可能只用一个单位计数，有时会用几个单位复合计数）这样的理解还可以进一步推广到小数、分数。

二、学生调研

1.设计前测试卷。

学生对数的认识情况如何？为探明教学的实际基础，我们设计了单元前测卷，以“单位”的思想为核心，主要测试两方面：（1）数的意义的基础认识；（2）应用数的意义解决问题。

前测卷“数的意义”部分，安排了多元表征的问题。

前测卷“数的应用”部分，设计了两位数与一位数以及两位数与两位数的加减法（加法不进位、减法不退位），包括直接计算问题和应用问题，应用问题又涉及加减法的各种情境意义，如合并、增加、减少、相差等。

2.学生实测结果。

杭州市胜利小学一年级共125 名学生参加了前测。实施时，学生在自然状态下，以课堂作业的形式完成前测。时间在30 分钟以内。期间，教师不做任何提示和点评。

结果发现：

（1）关于数的意义。

①对计数单位的认识掌握得不错。

如图4，前测卷第1 题、第5 题和第7 题，正确率分别达97.6%，96.8%和90.4%，从中可以发现学生对于计数单位的认识掌握得不错，能够通过语言、图像等准确表征23 的含义。说明浙教版教材前期对计数单位的强调，以及分段学习两位数的安排是有效的。

图4 两位数的多元表征考查题

②对数的抽象表征仍有困惑。

如图4，前测卷第4 题、第7 题和第8 题的正确率分别为80.8%，90.4%和88.8%，部分学生对数轴和算式这样数学化的表征仍存在困难和误会。

③自主表征的能力弱，数概念的结构化程度不高。

在“用图画出23”这道题目中，学生的作品可分类为——

计数器或数位表人数百分比（%）34.412.832.011.2表征方法散点图 以2，3，5 为计数单位的图像以10 为计数单位的图像请你用画图的方式表示23。请你用画图的方式表示23。请你用画图的方式表示23。请你用画图的方式表示23。样例images/BZ_14_1551_2250_1608_2444.pngimages/BZ_14_1718_2260_1866_2403.pngimages/BZ_14_1957_2257_2079_2412.pngimages/BZ_14_2137_2252_2272_2372.png

说明学生虽能看懂他人（教材、问卷）所提供的具有单位结构的各种数的表征，却没有内化为其自身的、自觉的对数的认识和把握，亦即学生自身的数概念还没有结构化。

（2）关于应用数概念解决加减法问题。

①对加法运算意义的掌握优于减法运算意义。

如图5，第10 题和第11 题是加法情境问题，正确率都是95.2%；第12 题和第13 题是减法情境问题，正确率下降为83.2%和90.4%。可以发现，学生对加法意义的认知优于减法，特别是减法中“相差比较”的问题，出现错误的情况最多。

图5 两位数加减计算考查题

②加法计算的正确率亦优于减法计算。

对第15 题两位数加两位数不进位的加法题，学生用到的计算策略有：a.先凑十，再继续加，如24+6+7，占33.6%；b.根据数的意义，相同计数单位直接相加，如：20+10=30，4+3=7，24+13=37，占36.8%；c.标准竖式计算，15.2%。对第16 题两位数减两位数不退位的减法题，学生用到的计算策略有：a.先减整十数部分再继续减，如69-30－7，占16%；b.根据数的意义，相同计数单位直接相减，如：60-30=30，9-7=2，69-37=32，占30.4%；c.标准竖式计算，15.2%。

学前加法的正确率为84%，减法的正确率为61.6%。在未学的情况下，初步能够利用数的意义自主寻求加减计算方法，但算理不自觉，算法不稳定。加法计算的正确率优于减法。

（3）关于数的规律问题。

在前测卷的最后，我们还安排了两个发现数规律的任务，如下图6。第17～20 题是数列规律的概括和推理，第21、22 题是数表规律的概括和推理。

图6 数列和数表规律推理

各题的正确率如下表——

题号171819202122正确率（%）99.270.472.882.475.246.4

可以看到，找规律问题的正确率整体低于前面的常规问题，特别的，学生虽然能够填出正确的数，但在表达规律时，能同时答到按不同方向“横看、竖看”和按不同维度观察“数位、数值”变化的人非常少。可知学生限于表面数字形式的感知，还没有能够深入到数的关系、计数的结构等层面深刻理解规律。

三、单元整合与重构

综上，我们考虑在实际教学中，对目前的教材编排做到一个“坚持”和一个“变化”。

1.坚持：突出“单位”的思想。

（1）坚持计数单位单独设课教学。

（2）充分展开计数单位计数的过程分析。

将整十数理解为以“10”为单位计数，而一般的两位数（几十几）是综合“10”和“1”为单位计数。注意对这样的认识过程及结果展开多元化的表征，发挥学生在表征过程中的自主性，并借助表征之间的比较、沟通和转换，帮助学生理解数学化的表征的意义，进而形成对数的结构化的认识。

图7 关于45 的各种结构化表征

（3）引导学生基于数的构成和运算意义，理解加减运算的基本算理。

利用学生目前“朦胧”的算法创造，引导学生基于数的单位去反思和分析各种算法的合理性、关联性，理解运算意义，对接计数规则，揭示运算原理，从而使学生的计算方法具有自觉性和灵活性，为今后进一步两位数进位加法、退位减法、多位数加减，甚至分数、小数加减等提供坚实的算理基础。

2.变化：增加学习的层次。

教材勾画的是最为理想的且条理清晰、层层递进的学习过程，而实际上学生需要在个人良莠混杂的认知内容中去伪存真、去粗取精，需要更多的学习时间，更丰富的学习活动去体会材料意图，反思活动经验，达到预定的目标。所以拟增加“我认识的100”“生活中的两位数加减问题”共两节活动课，贯通校内外的学习，赋予两位数认识以儿童的视角和个人的意义；另外对百数表“找规律填数”一课进行重构，突出规律表象与计数及计数规则之间的联系，引导学生感悟规律背后的数学本质。