基于模糊偏好与期望相似性的产品设计方案优选研究

刘芮葭，章 辉，李旭杰

（辽宁工程技术大学 工商管理学院，葫芦岛 125105）

0 引言

产品设计方案优选是继产品概念设计之后的又一个重要的环节，通过对设计方案进行评价并选择最佳设计方案，其将对后续的详细设计及优化环节产生重要影响。产品设计方案优选过程需要对多重指标进行整合，并对多个可行方案进行评价和排序S，因此产品设计方案优选是一种典型的多属性决策问题[1]。企业在产品的实现过程中，对产品设计方案的优选是企业所要面临的一个重要难题，为了更好地解决这个难题，需要以顾客需求为出发点对不同方案进行准确评价，并从中筛选出最有助于提高产品性能的产品设计方案[2]。将客户需求转移到产品设计中去，对企业做出正确的方案决策具有重要意义[3]。

产品设计方案优选一直是制造行业最关心的问题，国内外学者对如何进行产品设计方案优选已经做了大量研究，曾有学者采用模糊ANP[4]、灰色关联分析法[5]、案例推理法[6]和层次分析法[7]等对类似问题进行了研究。程晓娟等[8]立足于个性化定制行业，针对产品设计决策过程中出现的过约束现象，提出一种基于模糊偏好和约束层次理论的产品设计方案优选模型。王娟丽等[9]。

为了对设计方案作出更为全面和准确的评价，运用QFD、整数规划、全因子实验方案设计等方法建立了一种有效的设计方案评价模型。梁海明等[10]将决策小组的分布式群体感性评价值考虑进来，结合具有硬性一致型、硬性优势型和允许违反型三种类型的推理方法，提出了以随机占优准则为排序方法的产品设计方案优选方法。吕欣等[11]以产品设计方案评价过程中存在的片面性和主观性为出发点，经过长时间的文献研究和问卷调查，提出一种结合了AHP和TOPSIS法的方案评价优选方法。张文召等[12]针对方案评价过程中的主观性和模糊性问题，以问卷调查为手段，建立了一种基于模糊集、R-KANO、灰色关联分析和G-TOPSIS法的产品设计方案优模型。杨东[13]利用QFD方法建立了有效的产品设计方案指标体系和对应的指标权重。李金海[14]将QFD与TRIZ相结合，建立了新的产品研发模型，提高了研发效率。LUOXG[15]提出一种基于质量功能展开的（QFD）产品设计方法，通过质量屋和关联性分析将顾客最为关切的需求转化为工程设计相关属性。SHIPEI LI[16]提出一种基于模糊QFD的扩展概率语言方法，根据开放式设计中的顾客需求来确定工程特性的重要性权重。上述研究从不同角度对评价指标的确定以及方案评价过程中突发问题的解决进行了开创性探索，并取得了显著的成效。但以上研究对指标权重初始值以及指标属性初始值中部分值的精确性要求过高，在实际产品设计中，决策者往往很难得到所有有关设计指标的精确数值，对于某些属性值就需要结合有关专家的模糊评估来进行确定。并且这些研究都是基于可行方案集内部之间的比较评价与排序来确定最优方案的，由于缺少期望标杆方案，很难找到可行方案相对于期望方案的不足之处，无法提供后期设计的改进意见。因此，本文围绕产品设计方案优选问题，将模糊集理论与QFD相结合，从顾客需求出发建立产品设计特性及模糊关联关系矩阵，并运用模糊偏好关系分析确定了设计指标权重，最后引入期望方案，通过兼具精确和模糊信息处理功能的高斯相似性理论，对可行方案进行了有效评价与优选。

本文对产品设计方案进行优选的框架如图1所示。

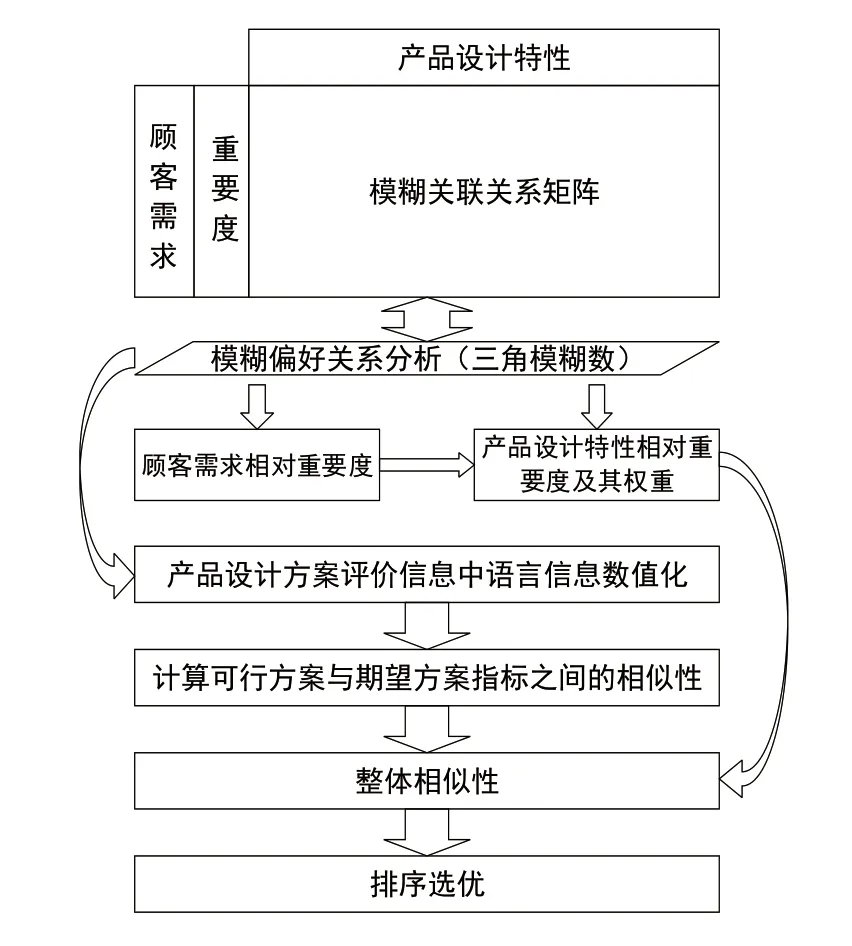
图1 研究框架

1 基于QFD的重要度分析

1.1 运用三角模糊数处理不确定性语言信息

为了便于产品设计方案优选后续工作的进行，本文首先利用三角模糊数对不确定性语言信息进行处理。

利用三角模糊数将表示专家Et（t=1，2，…，q）对顾客需求CRi（i=1，2，…，n）以及顾客需求CRi与产品设计特性DFj（j=1，2，…，m）间关联关系的不确定性语言信息转化成具体数值。

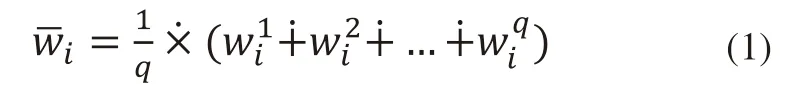
设Rqij是与专家Et对顾客需求CRi与产品设计特性DFj之间关联关系的评估结果相对应的三角模糊数，同样地，本文用其算数平均值均值来表示顾客需求与产品设计特性之间关联关系的群决策值：

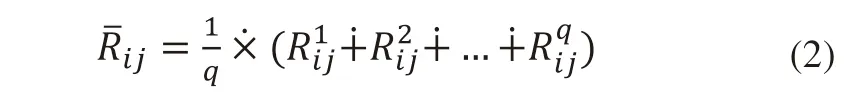
因此，顾客需求与产品设计特性之间关联关系矩阵R表示如下：

1.2 运用模糊偏好关系分析产品设计特性相对重要度及其权重

如式(4)所示三角模糊数是具有分段线性隶属函数μA的模糊数[17]。本文采用三粒度的语言信息集合，即S={差，中，好}，表1为语言信息变量与三角模糊数的对应关系，根据该关系将专家语言信息转化为三角模糊数，如式(1)的计算结果表示顾客需求的三角模糊数，式(2)的结果表示顾客需求与产品设计特性之间关联关系的三角模糊数。

表1 语言信息与三角模糊数的对应转换关系

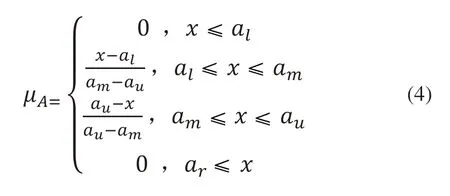
其中，A为三角模糊数，记A=（al，am，au），且al≤am≤au，其中al，au为三角模糊数A的上限和下限。

令X={x1，x2，…，xn}为一组三角模糊数，其中xi=（xil，xim，xiu），则该组三角模糊数的算术平均值表达式为：

其中‖T‖的表达式如下：

2 基于高斯相似性分析的方案优选

1）首先需要构建与在QFD分析过程中得到的产品设计特性相对应的产品设计方案评价指标体系。假设一共有s个可行方案，首先计算可行方案与期望方案各指标之间的差异程度[18]，Δ（pkj，poj）表示pkj与poj之间的差异程度，其中pkj指的是第k个可行方案Hk在第j个指标DCj下的属性值；poj指的是期望方案Ho在第j个指标DCj下的的属性值。

当属性值为具体数值时，Δ（pkj，poj）的表达式为：

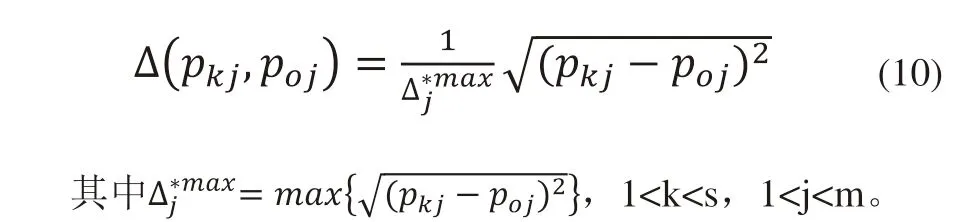
在实际操作中，某些指标的属性值难以直接用明确数值来衡量，而通常是以语言信息来表示，因此pkj，poj之间的差异程度此时就不能直接进行计算，所以本文需要将这类指标属性语言信息转化为三角模糊数进行计算。

假设pkj，poj对应的三角模糊数分别为（plkj，pmkj，prkj）和（ploj，pmoj，proj），则Δ（pkj，poj）的表达式为：

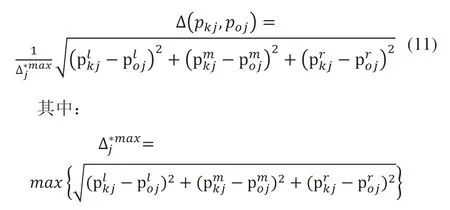
2）运用高斯相似性计算方法[19]计算可行方案与期望方案在第j个指标下的相似性。用Sim（pkj，poj）表示第k个可行方案Hk与期望方案Ho在第j个指标DCj下的相似性，Sim（pkj，poj）的表达式为：

其中δj表示第j个指标对应高斯曲线上的挠度。当指标为明确数值时，δj的表达式为：

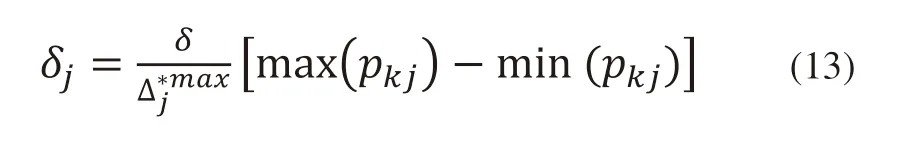
当指标为语言变量时，δj的表达式为：

3）求得可行方案与期望方案各指标的相似性之后，还需计算各可行方案与期望方案的整体相似性，令Sim（Hk，Ho）表示第k个可行方案Hk与期望方案Ho的整体相似性，Sim（Hk，Ho）的表达式为：

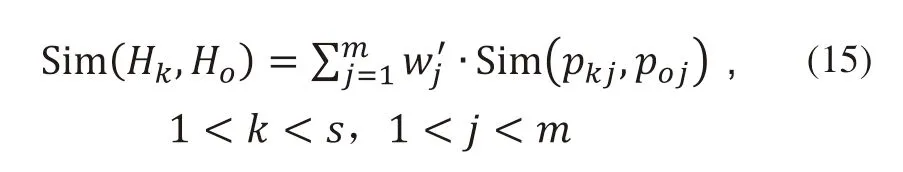
综上，基于QFD、模糊偏好关系和高斯相似性分析来对产品设计方案进行优选的步骤如下：

第一步：通过QFD分析确定以顾客需求为出发点的各产品设计特性及其与顾客需求之间的相互关联关系，并结合表1确定对应的三角模糊数，然后通过式(1)～式(8)中的相关算法分别求得顾客需求相对重要度以及产品设计特性相对重要度，并利用式(9)计算各产品设计特性的权重。

第二步：构建与在QFD分析过程中得到的产品设计特性相对应的产品设计方案评价指标体系，并确定产品各指标下的期望值，找出指标中属于语言变量的部分，通过表1中的对应关系将其转化。

第三步：求各可行方案与期望方案对应指标之间的相似性，首先，通过式(10)、式(11)计算各设计方案与期望间不同指标下的差异程度，接着通过式(12)、式(13)和式(14)计算各设计方案与期望方案间不同指标下的相似性。

第四步：求整体相似性，计算出各可行方案与期望间不同指标下的相似性之后，利用式(15)计算各可行方案与期望方案之间的整体相似性。

第五步：排序选优，根据整体相似性的数值由大到小排序，排名越靠前说明方案越理想。

3 实例分析

为了验证该模型的有效性，实例采用文[20]某重工企业有关装载机设计的数据，并将原五粒度语言信息变量重新分类为三粒度语言信息变量。在实例中，通过顾客访谈和调研获得以下六种主要的顾客需求：动力强劲（CR1）、灵活高效（CR2）、易操控（CR3）、稳定可靠（CR4）、服务及时（CR5）和低能耗（CR6）。从顾客需求出发而确定的产品设计特性对应的有：发动机额定功率（DF1）、最大掘起力（DF2）、斗容量（DF3）、最大卸载高度（DF4）、三项和时间（DF5）、最小转弯半径（DF6）、变速操纵方式（DF7）、预防性维修策略（DF8）、服务响应效率（DF9）、服务完成效率（DF11）、节能方案（DF10）、尾气排放标准（DF12）。

3.1 确定产品设计特性相对重要度

首先，运用专家语言信息对顾客需求进行评估，并计算出每种需求的相对重要度，结果如表2所示。

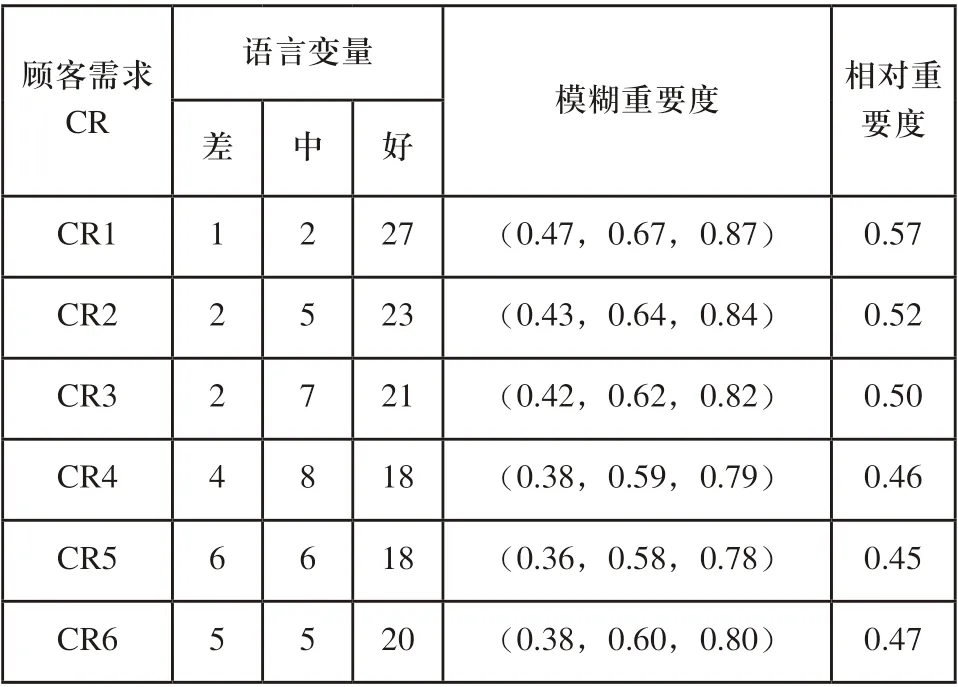
表2 顾客需求重要度的语言评估信息及其相对重要度

顾客需求相对重要度结果显示，各需求相对重要度都在0.5左右摆动，其中动力需求的相对重要度值最大，为0.57，服务及时性需求方面的相对重要度值最小，为0.45。但总的来说，各结果相对接近，说明顾客对每种需求的期待程度几乎都在同一水平上。

接着，采用专家语言信息对顾客需求和设计特性之间关联关系进行评估，然后通过表1将评估结果转化为对应三角模糊数，在此基础上，通过式(2)和式(3)建立顾客需求与产品设计特性间的模糊关联关系矩阵，并将表2得到的顾客需求相对重要度与该关联矩阵相乘求得各设计特性的模糊重要度，最后，根据式(5)～式(7)和式(9)计算产品各设计特性的相对重要度及权重，结果如表3所示。

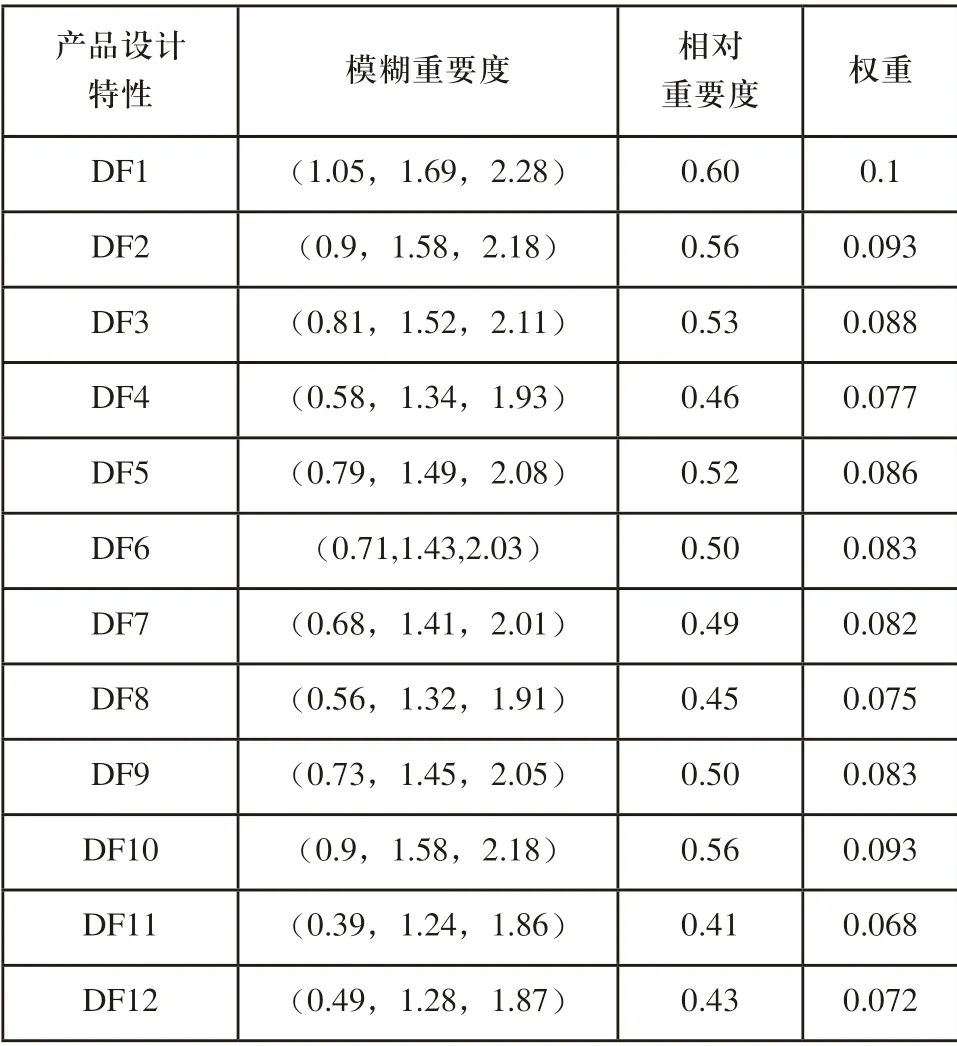
表3 产品设计特性相对重要性

3.2 构建方案评价指标体系并进行方案优选

针对企业额定载荷为3t的装载机，建立装载机设计方案指标体系，指标的类型、说明、变量类型以及取值如表4所示。

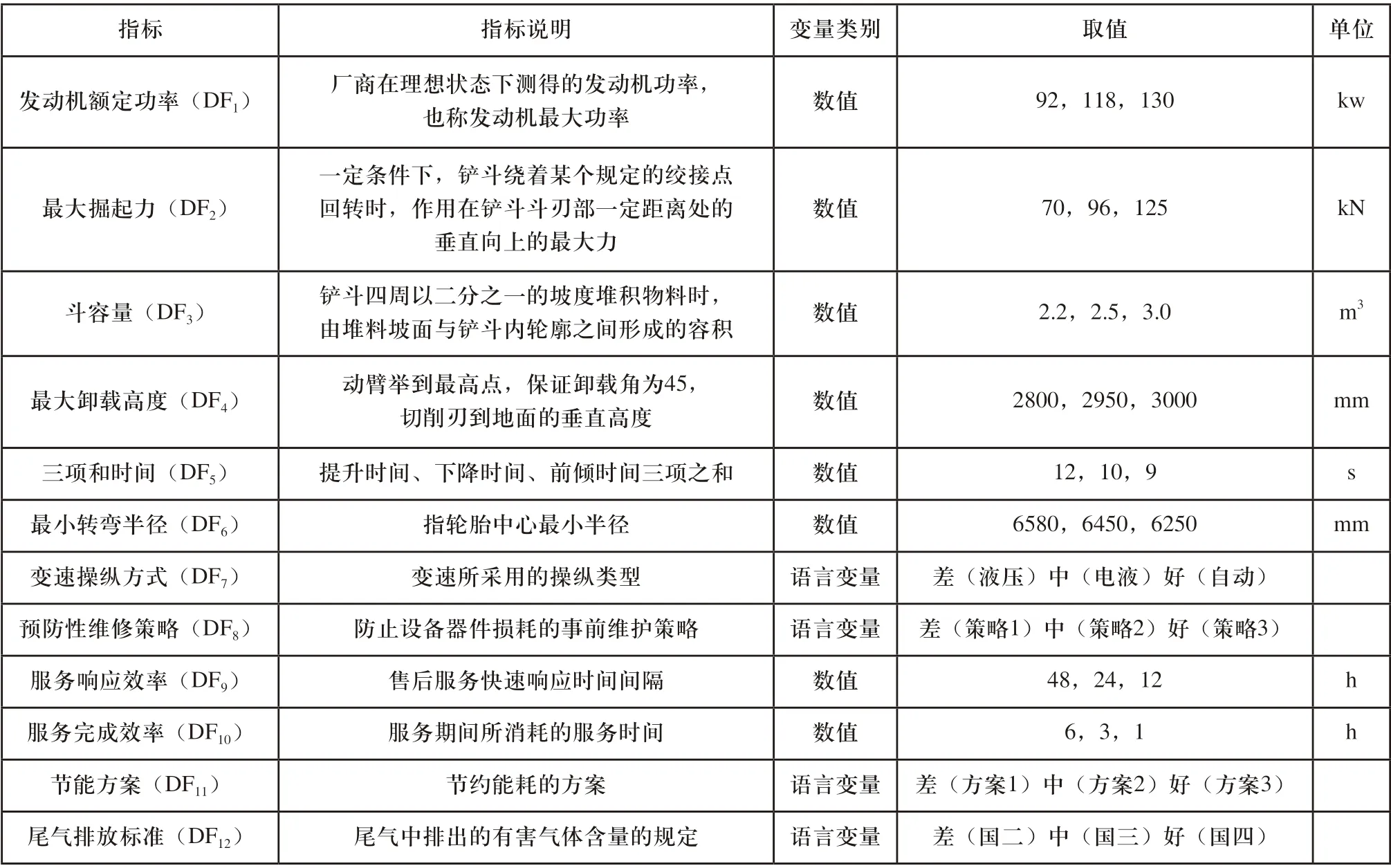
表4 设计方案评价指标体系与描述

针对该类重工产品，设计部门给出六种装载机设计方案，分别为H1、H2、H3、H4、H5和H6，本文以每个指标的最优值集合作为期望方案H0的方案指标来对各设计方案进行优选，各方案的指标信息如表5所示。

根据表1中的提到的各语言信息变量与相对应的三角模糊数的转换关系，对表5中的语言信息进行转化，具体需要转化的有DF7、DF8、DF11和DF12这四个指标，转化结果如表6所示。

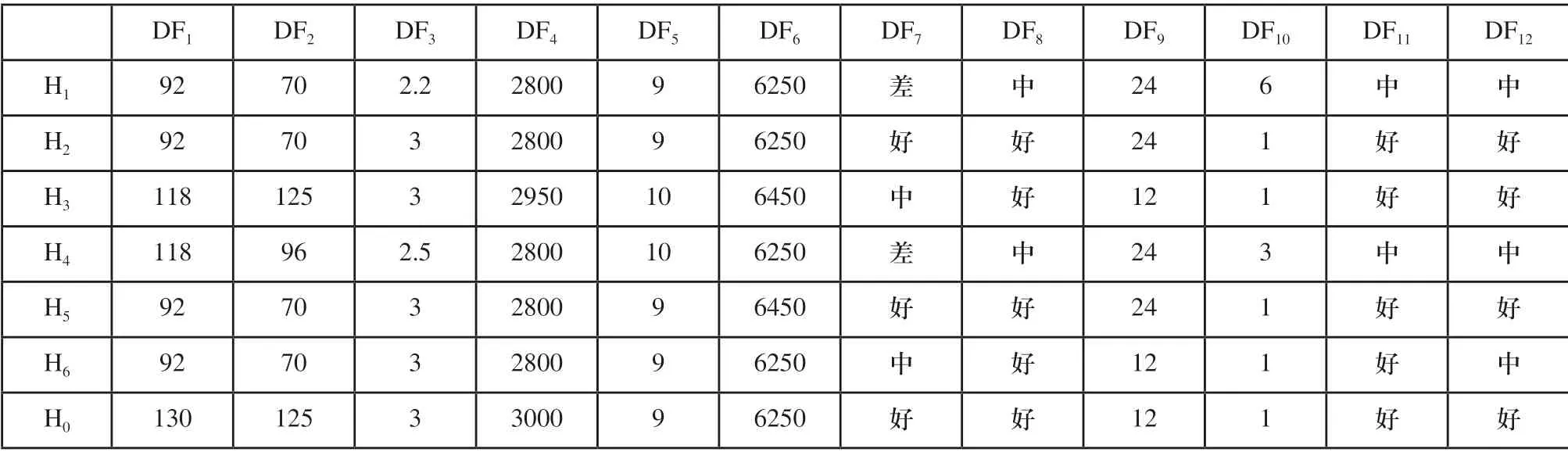
表5 各方案的指标信息

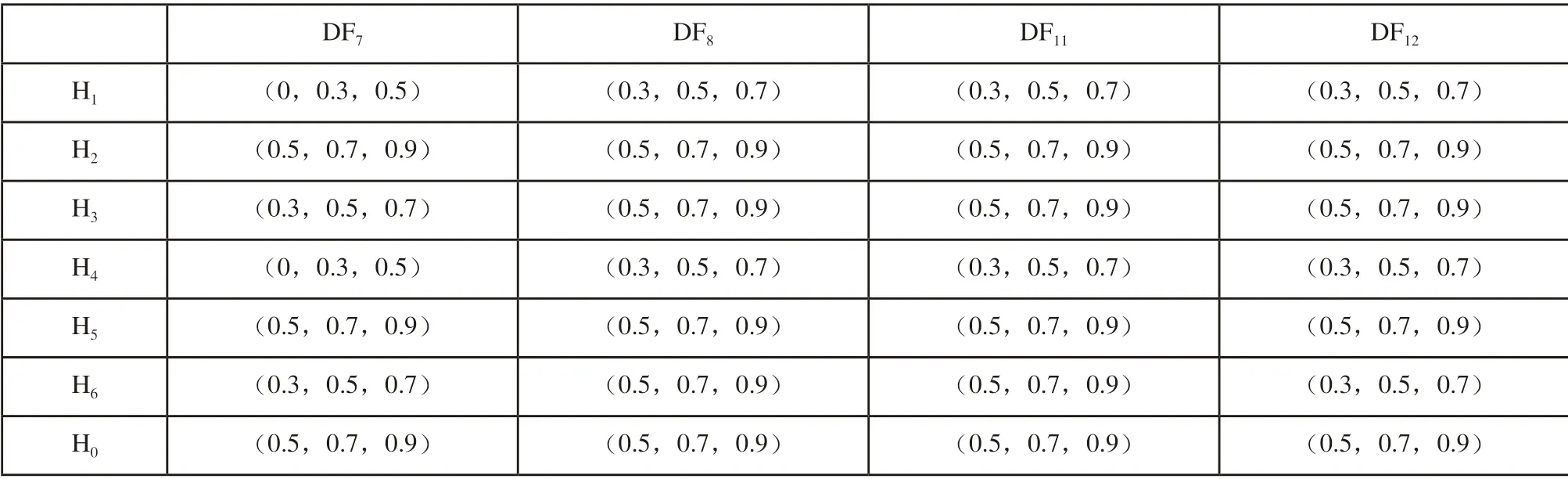
表6 语言信息转化为三角模糊数

确定了各指标的具体数值后，通过式(10)和式(11)计算各设计方案指标值与期望指标值之间的差异程度，结果如表7所示。其值越小，说明差异越小，比如当值为0时，说明设计指标值与期望指标值之间无差异；反之则差异越大，比如当值为1时说明设计指标值与期望指标值之间差异最大。而中间值则代表无差异至最大差异之间的差异程度。

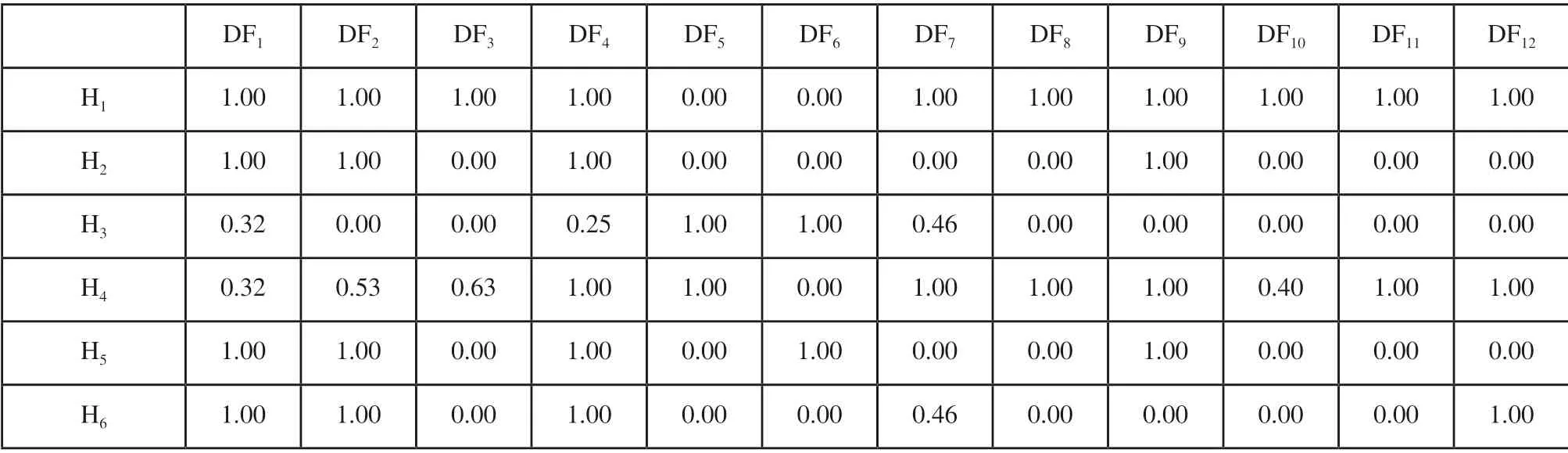
表7 各设计指标值与期望值之间的差异

接着，通过式(12)、式(13)和式(14)计算各设计指标值与期望指标之间的相似性，结果如表8所示。其值越大，说明相似性越大，如当值为1时说明设计指标与期望指标的值相同；反之则相似性则越小。需要说明的是此处没有相似度为0的值存在，对应于表7中的无差异和最大差异，相似性的结果也只有相同（完全相似）和最小相似性。并且，可以发现各可行方案与期望方案之间在某些指标下相似性并不高，说明设计仍然不够完美，还有改善的空间，以方案H3为例，其在发动机额定功率DF1、最大卸载高度DF4、三项和时间DF5、最小转弯半径DF6、变速操纵方式DF7等方面与期望方案还有一定差距，在后期设计中有必要加以提升。

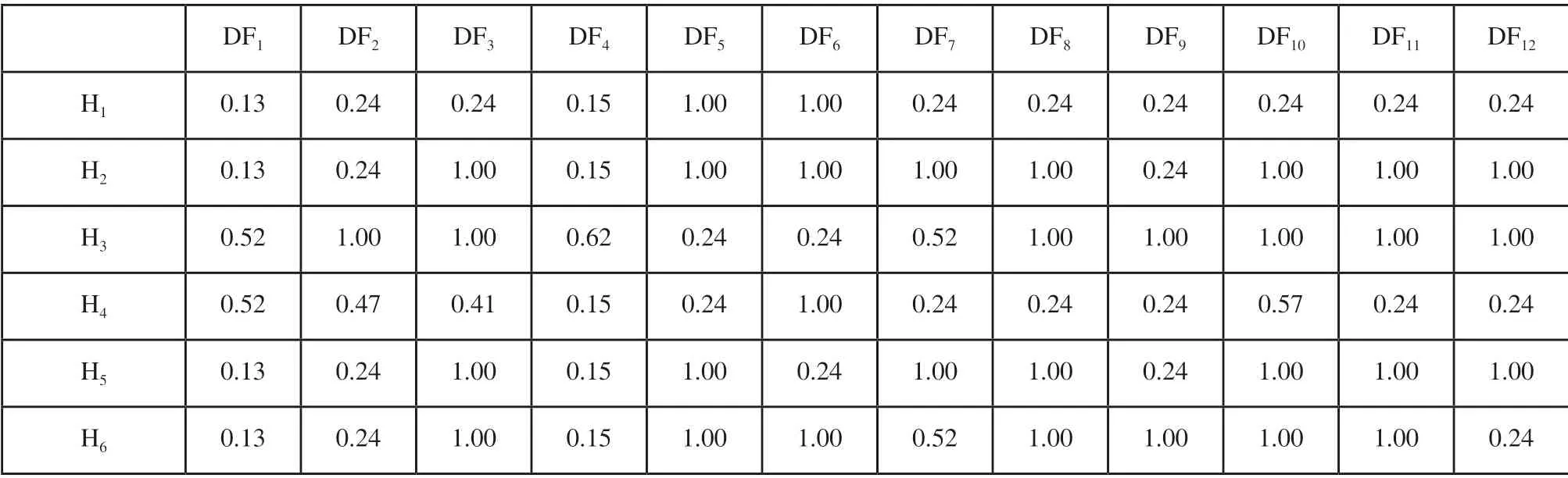
表8 各设计指标值与期望值之间的相似性

根据各产品设计特性权重值和各设计指标值与期望值之间的相似性值，通过式(15)计算各可行方案与期望方案之间的整体相似性，并对结果由大到小进行排序，最终结果如表9所示。

表9 各设计方案与期望方案之间的整体相似性

由排序结果可以看出，各设计方案与期望方案的相似性结果为H3>H2>H6>H5>H4>H1，因此对于额定载荷为3T的装载机的六种设计方案中，方案H3与期望方案最为相似，相似性值为0.7549，H3是最有可能应用到实际生产中去的方案。通过初始指标值可以看出，设计方案H3与期望方案在最大掘起力DF2、斗容量DF3、预防性维修策略DF8、服务响应效率DF9、服务完成效率DF10、节能方案DF11、尾气排放标准DF12七个指标上完全一致。而与期望方案相似性最小的方案H1，其相似性仅为0.3505，同样对初始指标值进行比对，不难发现设计方案H1与期望方案仅在三项和时间DF5、最小转弯半径DF6两个指标上的值相同。当然并不是具有相同指标值的指标数目越多就一定相似性最高，还必须考虑各项指标的权重及其指标值的具体大小，才能保证结果的客观准确性，如方案H4和H1，方案H4虽然排名靠前，但其只有一项指标最小转弯半径DF6的值是与期望值一致的，而方案H1虽排名靠后，但其存在两项指标三项和时间DF5、最小转弯半径DF6的值与期望值一致。

4 结语

本文运用QFD、模糊偏好关系、高斯相似性分析等方法，将顾客对于产品的需求转化为对产品设计方案进行评价优选的动因。克服了在数据精确度和方案评价中无期望标杆等方面存在的部分弊端，建立了有效的产品设计方案优选模型，使得企业产品设计者以及决策者能够快速地按照顾客需求，选出最能激发产品市场竞争力的产品设计方案。实例分析过程及结果证明，该方法能够将所有确定和不确定的决策信息都纳入考虑范畴，与期望方案进行相似性对比，既能有效选出最佳设计方案，也能显示出各方案与期望方案相比而存在的不足，有利于企业对产品进行进一步的改进升级，帮助企业在行业内同类产品的竞争中赢得更大优势。