交通路况感知下的自适应动态路径规划方法

常盟盟，袁磊，丁治明，李路通

(1.北京工业大学，信息学部，北京100124；2.中国科学院，软件研究所，北京100190)

0 引言

随着城市居民交通出行需求不断攀升，现有城市路网的承载能力不足给城市发展带来了巨大挑战。实际交通路网的状态复杂多变，高峰流量、天气、突发事故、交通管制等因素均会导致交通路网状态剧烈变化。如何提高交通运行效率，改善城市交通现状成为一个亟待解决的关键问题。传统的基于静态路网的路径规划方法，如Dijkstra、A*、Floyd 算法、遗传算法、粒子群算法、蚁群算法及其改进算法等，在路网状态动态变化过程中不能及时的做出有效的应对策略。同时，在大规模动态路网中，路径规划响应速度远远跟不上决策速度。针对上述问题，本文提出一种自适应的动态路径规划方法。首先，将路段上的路况信息融合到对路网区域的分析，对路网进行分层划分，提高路况分析的合理性；其次，在划分子网的基础上，采用层次扩散方法对子网间的路径传播进行建模，分析层次子网之间的连接关系，作为路径查找的扩展视野；最后，结合路径规划的实际需求，构建一种自适应的路径规划模型。与现有的经典路径规划方法相比，本文提出的规划方法填补了传统模型在路况变化下的可用性不足，扩展了路径规划模型对当下交通出行新需求的适应性。

1 相关工作

层次搜索策略则是结合道路网络的层次特征来提高路径的搜索效率。胡继华等[3]将出租车的路径选择经验作为语义，构建基于经验路径的网络。路径规划算法根据最短路和经验网络进行组合完成路径规划。在一定程度上复杂语义可以反映路网的动态变化特征，因此规划路径缩短了路径的旅行时间。另外，子图划分可以捕获网络中具有强连接关系的节点、区域以及同质的一些属性。Zakrzewska 等[4]提出一种动态网络划分算法，随着底层图的变化逐步更新被跟踪的子网。在每次更新过程中修改子网中的节点序列，从而将大规模网络的动态变化局部化处理。Rossetti 等[5]将图定义为二级实体，核心节点和外围节点。根据局部拓扑扰动动态跟踪子图的变化，利用局部模式和约束传播范围来减少节点之间寻址的计算开销。张正华等[6]提出一种交通子网划分方法，基于路段、排队长度等多维因素建立关联模型表示节点的重要性，对网络进行动态划分。区别于传统的图划分思想，流式图划分[7]一次处理部分图数据，并对于已分配到各个子图的节点不再进行迁移。在动态变化过程中调整节点之间的拓扑关系和权重变化。该方法可以有效地保留划分子图的性质，进而提升动态网络中路径寻址的性能。针对动态路网环境下道路状态的频繁更新问题，本文提出一种基于流式图划分的自适应动态路径规划方法，指导移动对象在路网行驶过程中能够自适应的避让或降低路况变化所带来的影响。

2 理论基础

2.1 动态路网下的路径规划

交通路网是一个随时间动态变化的有向图网络，可以定义为在一个时间周期内的网络状态，其中，T为变化周期，在这个周期内交通路网可以认为是一个静态的网络为路网节点集合，vi为其中的节点，i是节点编号，vi∈V，E为边的集合，ej为其中的有向路段，j是边编号，ej∈E。随着T的变化，路网G衍生出不同的时间快照G1,G2,…,GT。路径的起讫点(Origin-Destination，OD)分别来源于集合V中的两个节点，将从起点vo到终点vd的连通路径称为OD路径L。L由相邻的节点集合＜vo,vi,…,vd ＞连接而成，路段的旅行代价定义如下：

定义1(路段旅行代价)。设路径L中的两个邻接节点序列＜vi,vi+1＞来自于G中的路段集E，令表示δ在边＜vi,vi+1＞上的代价函数，则节点之间的旅行代价为

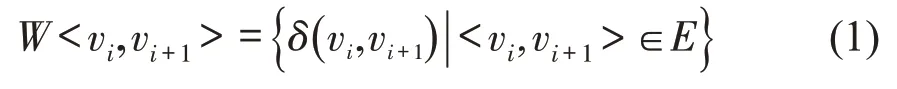
区别于常用的欧式距离度量，δ为随时间变化的映射函数。路径L的总代价，即求和连接OD对之间的路段代价为

式中：t0,t1,…,tn为变化的时间周期；vi为对应的抵达点；n为花费的时间步长；m为路段的个数。动态路径规划的问题域定义为在连续边集合E上的函数，通过寻找最小路径代价作为最优解。由于路网中的路段代价随着时间t发生变化，基于时间t的OD路径优化问题定义为

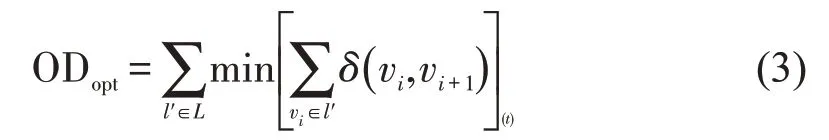
2.2 双向路径搜索2-Hop Cover

设计意图：教师引导学生明确遗传物质应该具有的特点，使学生能够理解为什么当时科学家会认为蛋白质是遗传物质。

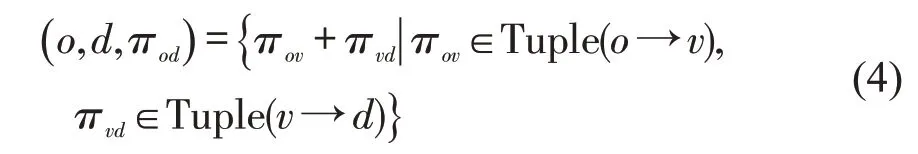
对于有向图G中任意给定节点o和d，其距离为D(o,d)，如果D(o,d)=ShortPath(o,d,Tuple)，那么该Tuple 就是图G中节点o到节点d的2-Hop Cover。在动态路网中，2-Hop Cover可以通过动态的调整局部的Tuple序列来适应路网拓扑和道路权重的变化，保持路径序列的代价最小。

3 基于路网层次划分的自适应动态路径规划算法

针对路网的动态变化问题，本文构建了一种基于层次划分的映射关系网络，将路径规划问题进行时空变化分解，规划路径伴随层次的变化进行实时调整，从而实现动态路径规划需求。如图1所示，OD请求通过查找路网层次划分结构获取最小包含子图G，函数ψ(t)更新子图状态。此时的路径规划算法依赖于子网中进行，在路径旅行过程中，若达到更新的下一周期t+1时，更新所在节点和目标节点的最小包含子网。从而路径L的子序列按照时间粒度t进行划分，伴随层次网络的变化进行调整，最终实现在动态路网环境中的自适应路径规划求解。

图1 基于子网划分的自适应路径规划模型Fig.1 Adaptive path planning model based on subnet division

3.1 动态路网层次划分

对于频繁变化的动态交通网络而言，区域划分是一个NP难题。现有的划分聚类在随时间变化的路网中，路网节点或边的聚类划分虽然提高了簇内的寻址效率，但对于簇之间的路径搜索因增加了划分约束而变得复杂。为了提高路径查找效率，通过预计算节点之间的连接关系Tuple，并在此基础上局部更新区域状态来提高路径查找性能。在每一步划分过程中，根据节点之间的层次关系预先计算节点之间的最短路径传播范围，并将相互分裂的节点二分为下一层子网，如图2所示。

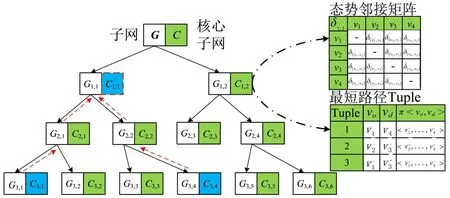
图2 动态路网层次结构划分Fig.2 Hierarchy structure partition of situational traffic network

层次结构中每个分支都代表一个子网G和对应的路径元组索引C，路径查询在网络快照中进行搜索。网络快照对应一个态势邻接矩阵，记录了相邻节点之间的旅行代价，具体如算法1。

算法1 路网层次划分Bisect G()输入：路网g，分裂个数k，划分粒度e输出：路网层次树h-tree if g 中节点数＜e return*h-tree end if for k 阶划分g.level←calmaxc()g ;/*根据中心性计算最高的节点等级*/for n in g if 节点n 的等级等于g 的等级添加n 到中心集合C end if end for end for split ←cluster(C,g)AddTree(*h-tree,split)/*按照C节点做k-聚类划分*/for each sub G in split /＊将子图添加到层次树结构中＊/Bisect G(sub G,k,e)/＊递归进行子图划分＊/end for

3.2 双向扩散路径查找方法

考虑如下OD出行需求，假设查找从叶节点G3,1的起点vo到G3,4的节点vd。从vo到vd的路径映射分为梯度扩散L(1)、双向探测L(2)阶段。路径决策沿着路径的梯度方向进行节点探测，即首先定位树中vo所属的子网(即叶子节点)，将中心性高于vo且梯度方向一致的节点加入探测队列。梯度∇f表示起点到目标点创建的方向向量，OD 路径轨迹沿着∇f，并通过近邻节点逐步扩散至目标节点。如果没有满足条件的中介点，则进入h-1 层子网，h表示G的层次。重复上述步骤获得满足条件的节点，选择距离最小的路径作为规划路径，即

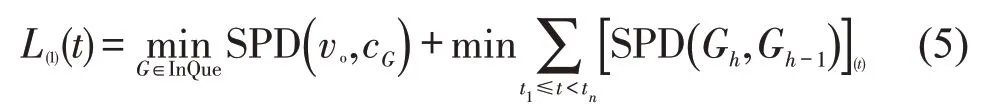
式中：SPD(·)为节点或子网中心之间的最短路径；cG为G的中心节点；Gh为h层的子网。为路径在t时刻的到达节点，在时间tn时，路径到达了目标节点的包含子网；L(1)为vo开始向所在子网的高中介性节点探测。

路径探测是在划分子网中进行最优路径的选择，随着路况变化如何决策最优路线是路径搜索的一个关键问题。为了提高查找效率，采用双向探测算法分别从起点和目标点进行正向和逆向的查找。L(2)定义为

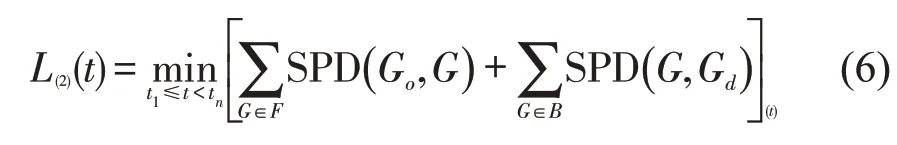
式中：Go、Gd分别为起点、目标点所在的最小包含图，F、B分别为正向、逆向的查找队列。当正向和逆向最短路径序列融合时，即为当前最优路径L(2)。最小包含图查找过程如算法2所示。

算法2 最小包含图查找FindMin G()输入：状态树Stree，起始节点o，目标节点d输出：最小共有网络Com G Sub G ←*Stree.root if Sub G 包含o，d Push Sub G into Com G /*起止节点同时位于该子图，将子图入队*/end if if Sub G 的右子树不为空if leftchild包含o，d FindMin G(&leftchild,o，d)/*起止节点位于左子树，递归左子树*/end if end if if Sub G 的左子树不为空if rightchild包含o，d FindMin G(&rightchild,o，d)/*起止节点位于右子树，递归右子树*/end if end if return*Com G

3.3 多路并行的双向路径探测算法

提出一种基于层次网络的多路并行动态探测算法(Multi-channel Parallel Dynamic Probing,MPDP)。MPDP探测算法融合了路况的时变状态，路径探测请求包含路径序列和路径累计权重。MPDP探测算法的具体步骤如下：

Step 1vo和vd根据状态树索引，采用BFS查找包含两点的最小共有子网Gmin(Min-Common Graph)。分别查找Gmin的左右子树，获得vo和vd所在的Go,Gd。

Step 2Go发送到达目标节点vd的路径探测请求，计算方向梯度∇f(G,vd)，并选择与∇f梯度方向一致的节点，作为传播的下一跳。Gd采用逆向递推序列选择与∇f一致的节点。

Step 3 按照∇f方向逐跳扩散，通过不断扩大节点的子网视野来，直到双向探测抵达Gmin，Gh作为Gmin的邻近祖先网络，作为扩展的接收视野。

Step 4 根据Gh得到k条路径序列p1=＜vo,u1,…,vd ＞，p2=＜vo,u2,…,vd ＞，…，pk，其中，ux为不同路径上的中继顶点。

Step 5 将备选路径p1,p2,…,pk上各中继节点路段的权重相加，得到对应的路径权重wp1(t)，wp2(t)，…，wpk(t)。

路径的跳数越多，在一定程度上增加了路径变化的可能性，引入正则化因子λ，量化子网跳数产生的影响，优化后的路径代价ωp(t)为

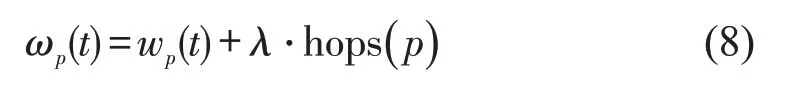
式中：hops()· 为统计路径跳数的函数。比较ωp1和ωp2,…,ωpk，选取最小路径代价作为t周期内的路径最优解。

最终，通过L(1)、L(2)分段路径映射算法，将OD路径L映射到时空域中，指导移动对象在旅行过程中根据路况变化进行动态调整，最终路径L收敛于终点。

4 实验结果与分析

为评价算法性能，实验采用北京市2012年12月实时路网数据集，采用开源数据集OpenStreetMap 提供的北京市路网，提取了车辆行驶的132039 个路段和92340 个节点，信息采用50000 多辆出租车近13 亿GPS 时间序列轨迹点聚合而成，更新周期为38 s。实验环境为Intel(R)Xeon Silver 4210 CPU@2，20 GHz，64 GB 内存，Windows10 64位操作系统。

实验参数设置：在h-tree的同一层次中，层次划分k值的选择关系到路径所经过的子网个数。对于跨子网的OD路径，所经过的子网序列的最大值为2(k-2)-1,k≥2。为了提高子网间路径的查找效率，同时降低子网跳数增加所带来的潜在态势变化，k取值为2。划分粒度e依赖于实际的路网规模，以北京市路网(包含92340节点)为例。CH算法采用节点收缩过程构建了104928 条捷径，通过节点关联进一步聚合为2143个层次指导路网的语义划分。因此，等同的将最小划分粒度e设置为[92340/2143]=43。

将本文提出的路径动态探测方法MPDP 与Dijkstra，A*，CH，动态A*算法进行实验对比。为了捕捉路网对路径规划造成的影响，在北京市实时路网数据上进行不同时段的实验设置。表1为8:00和14:00 对路网中OD 点对进行路径请求，对应其平均访问节点个数。

表1 路网OD对路径请求的实验结果Table 1 Results on path requests of OD pairs

在算法查询性能方面，Dijkstra 扩散过程采用贪心算法，迭代计算其到n阶邻居节点的最短路径，8:00平均寻址节点访问总数为57671，其单次查询耗时为126 ms，时间复杂度最高。A*和动态A*算法在路径搜索过程采用启发式策略，在很大程度上降低了不必要的访问节点，其访问节点总数较Dijkstra 降低了37.56%和76.32%，请求时间最小降低到88 ms。CH算法通过进行节点收缩的预处理，减少了路径查询所依赖图的体量来提高路径查找性能。其对应的访问节点总数为462，在查询时间上提速为98 ms。然而CH 算法中的节点依赖于快照，需要额外的从快照中恢复计算实际节点。MPDP算法采用了分层的图划分方法，其检索范围小于CH 基于全局节点收缩的图快照，故其访问节点数和响应时间均高于上述模型，最小访问节点数为378，响应时间为56 ms。图3为不同方法在不同起点时刻的查询性能。差异性越大表示模型的鲁棒性越好。可以看到，Dijkstra，A*和CH 算法的查询性能并没有发生显著变化，而动态算法的差异性较大。查询性能依赖于模型路径查找的时间复杂度，不同模型的访问节点数随着路网态势的增加有所提高，这是由于路网变化导致原来的最短路径序列失效。路网中OD 平均路径距离在14:00 为1675.32 m，在8:00 增加到1821.34 m，两个时刻路网状态下Dijkstra，A*和CH 算法的查询耗时差异为0.90%,3.00%和9.18%。动态A*算法能够根据路网变化作出调整，其差异为35.38%，但其查询耗时较大。MPDP算法其差异值为9.80%并且查询耗时最小。因此，针对路况变化动态路径规划算法具有更好的鲁棒性和查询性能。

图3 不同模型的单次查询耗时对比Fig.3 Comparison of single query time of different algorithms

路况的时变性导致在不同起点时刻，路径规划算法下的旅行耗时不同，如图4所示。选取北京市OD 起讫地点(40.019201,116.354828),(39.778991,116.353455)，分别在8:00 和14:00 进行不同的路径规划算法。在14:00，5种方法计算得到该起讫点的相同路径序列包含187 个节点，如图5(b)所示；在8:00，Dijkstra，A*和CH算法采用14:00时的相同路径，动态A*和MPDP 算法根据路况变化得到包含157个节点的新路径，如图5(a)所示。

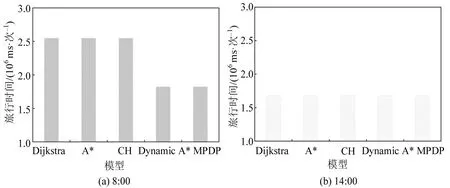
图4 不同起点时刻的旅行时间变化Fig.4 Time-consuming in travel at different starting time

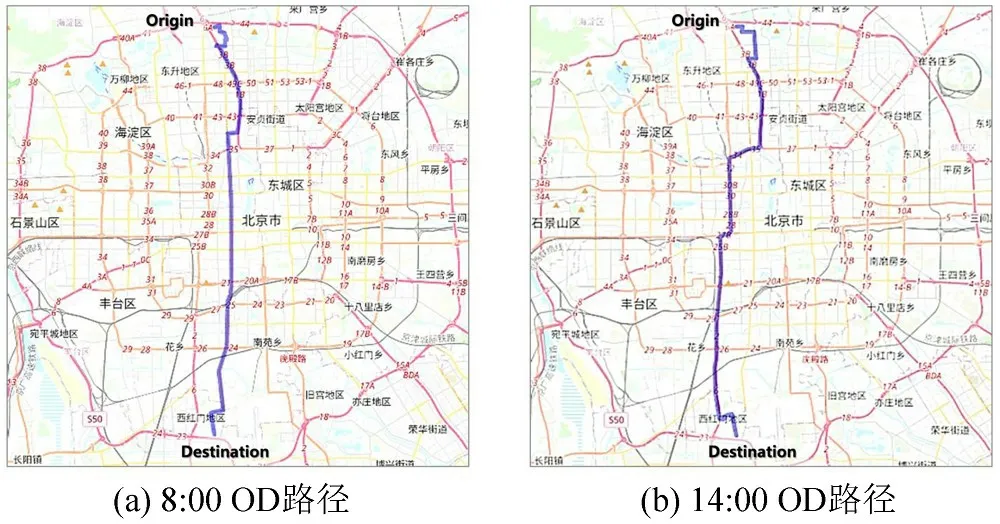
图5 相同OD对在不同路网状态下的最优路径Fig.5 Optimal path for same OD pair in different road network situations

同一算法在不同起点时刻计算出的路径旅行耗时不同，这是由于路况变化导致路段的通行能力降低。在14:00，不同算法的路径旅行时间并没有显著差异，可以认为路网状态接近于静态路网。对比8:00 的路径耗时可以看出，随着路况变化的增强，传统的静态路网规划算法没有对这些受影响路段进行规避，导致旅行时间延长。而动态A*和MPDP 路径规划算法可以有效地降低路况变化引起的增量代价，提高预估到达时间的准确性。

路况变化同样对路径规划算法的节点探测范围产生影响。对于静态网络模型，路径探测通过一次执行来完成，即仅与路网上一时间快照的状态相关。因此，节点探测过程保持不变，如图6(a)和6(b)中的Dijkstra，A*和CH 探测曲线比较一致。对于动态A*算法，在8:00的探测节点总数为13248。相对于Dijkstra，A*算法能够通过较小的节点访问量和探测距离，抵达目标节点。这是由于动态A*算法可以在旅行过程中，根据路径启发函数动态调整下一阶段的行驶路径。然而动态A*算法依然需要访问大量的节点进行对比计算，从而做出合理决策，因此动态A*算法的节点访问量较高，其节点访问总数和探测范围为13248和120031。CH探测算法通过预处理对节点进行筛选，因此CH 算法的节点访问总数低于Dijkstra，A*和动态A*算法。CH算法通过节点收缩聚合生成整个路网的核心主干网络，然而其对每个节点的重要性计算采用平等的衡量指标，难以适应环境下动态变化的节点优先级，因此其探测范围为345814 高于动态A*算法。MPDP算法结合动态A*和CH算法的优点，通过层次划分方法，减少了路径探测的节点总数，同时根据划分子网之间的寻址关系有效减少了路径的探测距离。并且随着变化能够动态调整访问节点和探测范围，说明MPDP算法对变化的路网具有良好的鲁棒性。

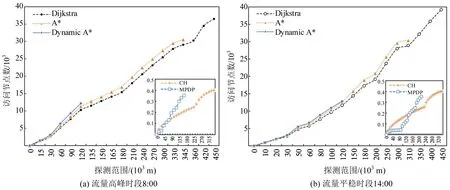
图6 不同影响下的路径探测范围Fig.6 Path detection range under influence of situations

5 结论

本文在所提出的动态路径索引的基础上构建了多路并行的路径规划方法，通过实验验证了时空索引树有助于对动态路网的快速建模，提高了传统路径规划方法在动态路网中的适用性。同时得出，在动态路网中不考虑路况状态的路径规划方法需要昂贵的计算代价和耗时，而降低动态路网所带来的附加代价必然需要路径规划模型从时空角度进行优化。本文提出的动态路径规划方法在计算过程中融合了时空变化特征，在空间上通过索引结构缩小路径查找视野，同时周期性的对路网状态进行更新，从时空角度对路径规划过程进行调整，这也是对基于静态路网的路径规划方法的一种新扩展。