基于时空等待特征系数的大型活动出行规划研究

胡臣杰，张军

(1.北京航空航天大学，电子信息工程学院，北京100191；2.阿里云计算有限公司，杭州310024；3.北京理工大学，前沿交叉科学研究院，北京100081)

0 引言

近年来，随着综合国力和国际影响力的稳步提升，我国承办国际大型活动的次数显著增加。大型活动吸引大规模客流带来巨大经济收益的同时，也给城市路网带来了巨大的压力，影响人们日常的生活出行。大型活动中不同角色的活动参与者在交通出行模式上存在多维度的差异，其中，观众群体以其数量众多、来源地广泛分散、可选交通方式多样等特点引起活动组织方与交通部门的关注。为广大活动参与者提供合理、安全、高效的多模式交通出行路径规划方案是维护大型活动交通秩序和为公众提供高质量交通服务的重要保障。

国内外学者针对大型活动交通组织管理，乘客多模式出行规划及诱导等方面发表了相关研究。叶霞等[1]从人流预测的角度提出大型活动散场时的人群疏散模型，并基于调度优化算法求解疏散方案，提高人群疏散效率。GOERIGK 等[2]考虑观众乘坐巴士进行疏散，有效处理不同规模的疏散问题。CORDEAU等[3]提出变体禁忌搜索算法求解大型活动中车辆路径优化问题。在多模式出行规划相关研究中，研究者依据场景特征提出多种模型。LOZANO 等[4]提出多模态超图和可行超路径的概念，定义了多模式交通网络中的最短可行超路径问题。佟路[5]等研究基于时空可达性的网络设计问题，提出基于时空网络模型和拉格朗日分解的公共交通路径规划方法。李浩楠[6]将马尔可夫决策过程引入多模式交通网络路径规划建模中。针对大城市多模式交通出行中的乘客换乘与非线性票价因素，LO 等[7]提出状态增强多模式网络，并与嵌套Logit 方法集成，通过案例研究票价竞争对公司盈利能力与网络拥堵的影响。FU 等[8]在多模式交通网络中引入一种新的基于活动的时空可达性度量指标，建立双层规划模型并设计人工蜂群算法，优化公共交通线路的车头时距与票价。在考虑诱导信息的出行问题研究方面，基于对交通网络中出行者选择行为的分析，韩凌辉[9]将出行信息诱导与基础路网的连续网络设计结合，设计了一种交通管理方法。更进一步，宋翠颖等[10]提出基于智能手机车内拥挤信息的乘客公交路径选择模型，考虑乘客获得拥挤信息后出行与换乘的策略调整，为智能化交通出行选择提供有效方案。SONG等[11]结合乘客对出行时间、换乘时间和等待时间的不同偏好，探究乘客获得智能手机实时交通信息对节约出行成本和公共交通线路负荷的影响。ABANE[12]调查斯里兰卡部分居民的出行行为，通过定量研究，得出家庭收入、出行安全及舒适度等因素会影响出行者的出行行为。基于公共交通网络的特点，吴震宇[13]对出行者路径选择模型进行数学描述，并设置广义出行费用函数，引导出行者的路径选择。

已有研究少有针对大型活动中观众群体的公共交通路径规划，涉及群众出行路径规划的研究也极少考虑乘客的个体出行偏好。鉴于大型活动规模不断增加与乘客出行选择日趋多样的现状，综合考虑上述因素以保障大型活动的举办亟待研究。本文提出面向乘客出行偏好的时空等待特征系数，建立基于时间-空间-交通方式网络的多模式交通路径规划模型，以乘客出行时间成本最小为目标函数。在此基础上，提出基于拉格朗日松弛的次梯度下降算法进行求解，从而为出行者提供个性化出行规划方案。

1 面向乘客偏好的时空等待特征系数

出行前，乘客将根据出行目的与个人偏好计算备选路径的成本，比较并选择最佳出行方案。在众多出行成本的计算方式中，出行时间是不可忽视的关键因素。出行时间包括：行程时间、换乘时间和等待时间。其中，行程时间指乘坐交通工具时间，换乘时间指乘客在站点内换乘不同交通方式的时间，等待时间指从抵达站点到乘坐交通工具等待所需时间。出行过程中行程时间及换乘时间通过出行路线确定，而等待时间因乘客不同选择而不同。空间上相同的出行路径，不同乘客可在同一站点等待不同的时间以乘坐不同车次的车辆。经调研分析发现，等待时乘客考虑的主要因素为舒适度及交通方式的可靠性[13]。其中，舒适度由等待场所的基础设施建设程度及交通拥挤程度决定，交通方式的可靠性受车辆到站的准点程度和车次间隔的均匀程度等影响。本文对于每个等待场所的3 个指标均采用5 等级李克特量表进行量化。基建程度F的取值为1.00，0.50，0.30，0.25，0.20，值越低，基建程度越低；拥挤程度S的取值为1，2，3，4，5，值越高，拥挤程度越高；交通工具可靠性R的取值为1.00，0.50，0.30，0.25，0.20，值越低，可靠性越低。本文提出基于乘客偏好的时空等待特征系数，表达乘客对出行过程中某个地点对影响等待决策的不同因素的关注程度。进行等待成本计算时，为等待场所的基建程度F、拥挤程度S及交通工具可靠性R等因素加个体偏好系数θ，不同的出行者，偏好系数θ不相同，但同一名乘客的所有时空等待特征系数θ之和为1。面向个体出行偏好的等待成本公式为

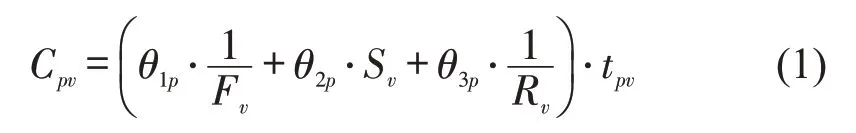
式中：Cpv为乘客p在节点v处的等待成本；tpv为乘客p在节点v处的等待时间；Fv、Sv、Rv分别为节点v处基建程度、拥挤程度及交通工具可靠性，基建程度越高，拥挤程度越低，交通方式可靠性越高，等待成本越低；为乘客p对不同因素的关注程度，。

是否考虑乘客出行偏好的不同等待成本如图1所示。以某乘客为例，图1(a)实线表示在不同节点处设置不同等待成本；虚线表示不进行区分。其中，v1、v2、v3和v4分别表示不同的等待地点，c1、c2、c3和c4表示乘客在对应地点的等待成本。图1(b)表示对不同节点处的等待成本加以区分时，若等待总时间相同，在各点处的等待时间分配将影响出行过程中的累积等待成本。图1 中，T1、T2、T3和T4分别表示不同的等待时间，和表示考虑出行偏好后乘客等待不同时间的累计等待成本。因此，引入面向乘客出行偏好的时空等待特征系数将影响乘客的时空出行路径。

图1 考虑乘客出行偏好的等待成本示意Fig.1 Schematic diagram of waiting costs considering passenger travel preferences

2 基于时空等待特征系数的公共交通出行路径规划问题建模

2.1 问题描述及相关假设

固定的运行线路与周期性运行时刻表组成了单一公共交通方式的运行方案。运行方案可以通过公共交通时空网络进行建模。其中，空间维度包含站点位置与运行线路，时间维度包含车辆在站点间的行驶时间和在站点的停车时间。乘客出行过程可以抽象为点在网络中通过时空弧的移动。公共交通时空网络如图2所示。

图2 公共交通时空网络Fig.2 Time-space operation diagram of public transportation

实际中，单一公共交通出行往往不能满足观众参与大型活动的交通需求，观众基于经济性、时效性、舒适性等多方面考虑，通常会选择综合公共交通方式组合的出行路径。本文将交通方式设置为新的维度，建立时间-空间-交通方式网络。

2.2 时间-空间-交通方式网络

以观众参与冬奥会为例，建立的网络如图3所示，其中，横轴表示时间，纵轴表示位置，竖轴表示交通方式。此外，由于不同的交通方式具有不同且固定的运行计划，因此，在时间-空间平面，每一层具有不同的网络结构。同时，由于不同交通方式的换乘仅在某些站点可以实现，所建立的空间-交通方式平面的网络边应与实际情况保持一致。图3中，实线为观众的出行路径；虚线为出行路径在空间-交通方式平面的投影，表示换乘路线；点划线为观众位移轨迹。

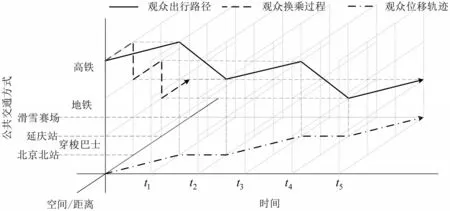
图3 时间-空间-交通方式网络[5]Fig.3 Time-space-transport mode network diagram

2.3 时间-空间-交通方式网络设计步骤

2.3.1 构建时空点集合

将一维空间点集N、离散时间点集T、备选交通方式集合M做笛卡尔积，生成时间-空间- 交通方式网络点集：V=N×T×M=。

2.3.2 构建时空弧集合

时空旅行弧：对∀a∈M，根据对应交通方式运行规划，在相邻到达的时空点对与间建立时空旅行弧，并将其添加至时空旅行弧集合E。

时空换乘弧：若某点同时有两种或以上的交通方式可通过，即存在时空点对和，则可在该时空点对间建立时空换乘弧，并将其添加至时空换乘弧集合C。

时空等待弧：对∀i∈N,a∈M，用时空点对和表示乘客在原位置原交通方式处进行等待，因此，可在时空点对间建立时空等待弧，并将其添加至时空等待弧集合W。

2.3.3 设置时空弧对应成本

2.4 模型建立

2.4.1 目标函数

模型的目标函数为所有乘客的出行时间成本之和最小。出行成本包含3 部分：旅行成本、换乘成本和等待成本，模型的目标函数为

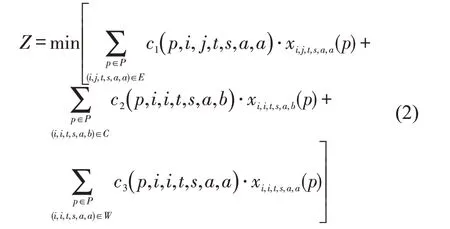
2.4.2 出发地约束

保证任意乘客p从出发地前往确定的出发站点，乘坐公共交通工具完成出行的约束为

式中：φ(O)(p)为符合乘客p出发地设置的可出行线路集合。

2.4.3 车辆满载率约束

考虑不同交通方式具有不同承载能力，使得选择相同时空旅行弧出行的乘客数不超过对应最大承载率H(Cap)(a)。此外，基于常态化疫情防控措施，应适当下调满载率以保证合适的社交间隔，设修正因子为α，则实际车辆满载率为α·H(Cap)(a)。车辆满载率约束为

2.4.4 时空网络流平衡约束

网络流模型中基本的流平衡约束是保证每个时空点的流量平衡，即

式中：对于乘客p，O(G)(p)、D(G)(p)分别为出发地与目的地；O(T)(p)、D(T)(p)分别为最早出发时间与最晚到达时间；O(M)(p)、D(M)(p)分别为出发及到达时所使用的交通工具。

2.4.5 决策变量约束

保证决策变量xi,j,t,s,a,b(p)的取值为0或1，即

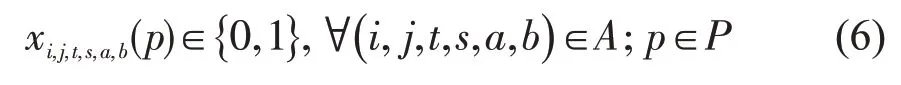
3 基于时空等待特征系数的多模式出行路径规划模型求解算法

时空网络特征系数具有降低建模难度，减少复杂约束及增加模型理解性的优势，但将模型应用于真实数据集时，求解速度慢仍是难以忽视的难题。因此，本文提出一种基于拉格朗日松弛的优化算法。

3.1 基于拉格朗日松弛的时空网络多模式出行路径规划求解

针对所提出的模型，本文对所有约束中最为复杂的车辆满载率约束使用拉格朗日松弛理论进行松弛，最大程度简化问题。设拉格朗日乘子λi,j,t,s,a≥0，得到对偶函数为

对应的，得到对偶问题为

约束条件为式(3)、式(5)及式(6)。ZLR(λ)的解为原问题解的下界，本文采用次梯度优化算法求解提出的对偶问题。

3.2 次梯度优化算法设计

次梯度优化算法通过计算次梯度更新拉格朗日乘子，迭代求解对偶问题。次梯度优化算法流程如下：

Step 1 初始化

给定循环次数限制m及提前终止阈值ε，初始化拉格朗日乘子λi,j,t,s,a,0。

Step 2 拉格朗日对偶问题求解

Step 2.1 将乘子的值代入松弛子问题进行求解，得到当前步最优解xi,j,t,s,a,b(p)。

Step 2.2 将变量xi,j,t,s,a,b(p)的值代入对偶问题ZLD，求出最优解的下界。

Step 2.3 检验解是否满足原问题约束式(4)，若满足，说明当前解为原问题可行解，亦为最优解，算法终止；若不满足，采用贪婪算法将不满足原问题约束条件的解的相关部分进行可行化处理，得到最优解的上界。

Step 3 拉格朗日乘子更新

Step 4 终止条件检验

Step 4.2 判断迭代次数是否超过m，若超过，中止算法；否则，返回Step 2。

4 数值实验及分析

4.1 参数设置

为验证模型正确性与算法有效性，本文以2022年冬奥会为背景进行算例实验。假设观众参与观看国家高山滑雪中心某日11:00 的比赛，以北京市内10 个地铁站为开始交通节点，观众从市内乘坐京张高铁前往延庆赛区，延庆赛区内设有2个班车服务点，观众通过乘坐班车从高铁站到达比赛场馆。实际交通网络如图4所示。

图4 实际交通网络Fig.4 Actual transportation network diagram

本文统计了不同交通方式的出行时刻表。

(1)地铁时刻表

13 个地铁站相邻站点间运行时间及高峰期发车间隔如表1所示。

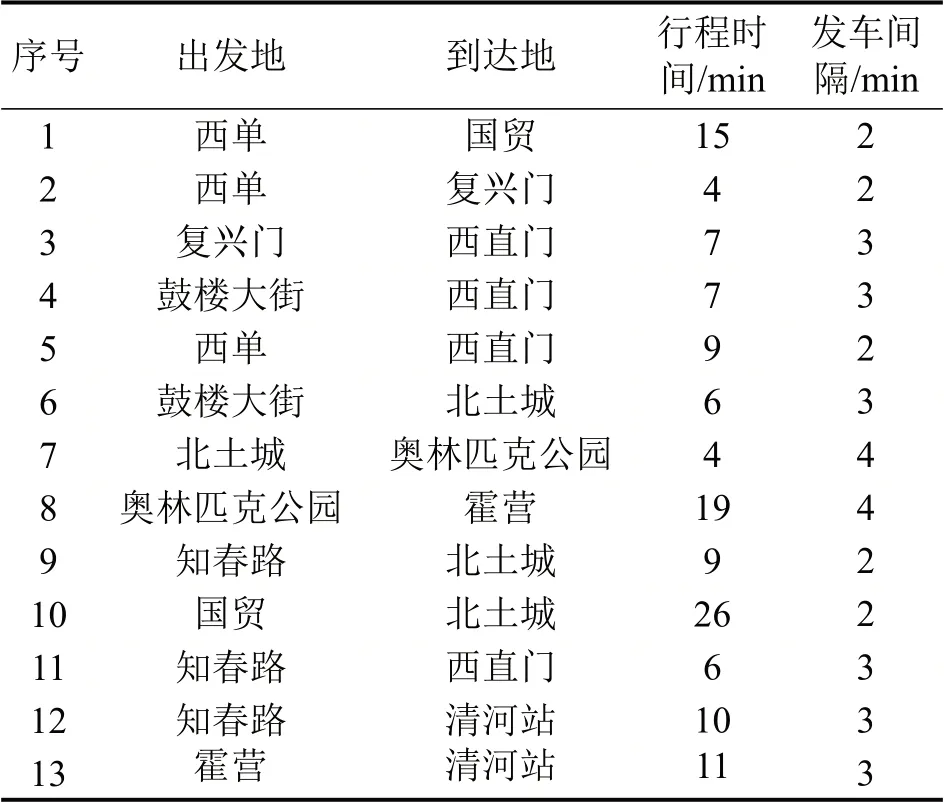
表1 地铁发车时刻表Table 1 Subway departure timetable

(2)高铁时刻表

前往观赛的观众可以乘坐京张高铁从北京市区抵达延庆赛区，符合出行需求的高铁班次为：6:00 从清河站出发，于6:26 抵达延庆站的G8881次高铁；8:51 从北京北站出发，9:06 途径清河站，并于9:37 到达延庆站的G8883 次高铁。观众可根据出行需求选择出发高铁站。

(3)班车时刻表

从延庆高铁站至国家高山滑雪中心赛区班车频次设置为5 min·班-1，每趟的行程时间为35 min。

(4)换乘时间设置

实验中将地铁换乘高铁的时间设置为30 min；高铁换乘班车的时间设置为15 min。

(5)面向乘客出行偏好的等待成本设置

由于每位乘客对等待时各种因素的敏感性不同，因此，为每个个体随机生成3个取值均在0～1间的偏好系数θ1、θ2、θ3，并将其进行归一化处理。然后为乘客出行的不同节点设置基础设施建设程度值Fv、拥挤程度Sv以及交通工具可靠性Rv。不同节点情况不同：①乘客在出发地等待舒适度高，拥挤程度低，基建程度及可靠性都极高；②地铁站因举办大型活动发生拥挤，但班次间隔小，有较高的可靠性；③高铁站基础设施较好，且实名制购票使得可靠性较高，但仍可能发生拥挤；④户外班车站基建程度较低，大量观众排队上车，可靠性差；⑤赛事场馆，持票观众进入场馆落座不存在拥挤状况，且由于已经抵达赛场，出行路径已完成，故可靠性高。各类节点的取值如表2所示。

表2 不同节点的Fv、Sv、Rv 取值Table 2 Values of Fv,Sv,Rv for different nodes

(6)其他设置

对于不同交通方式，使用交通工具的容量也有所区别，本文根据实际情况按比例设置每种交通工具所能搭载的最大人数限制。

4.2 案例实验结果分析

鉴于本文模型复杂、搜索空间庞大，规划大规模观众路径的求解效率较低，因此，提出了一种基于逆向推断的搜索空间约减方法，即在进行案例实验时基于所考虑场景的特点，通过倒推的方式对搜索空间进行约减。在本文的设置下，若观众欲观看11:00的比赛，据京张高铁现行运行时刻表倒推，得出此名观众需8:51 从北京北站或9:06 从清河站乘坐G8883次高铁抵达延庆站，并推断乘客应在7:30-8:30区间乘坐地铁出发，在9:37高铁到达延庆站后换乘班车，抵达高山滑雪中心。经统计，使用该种约减方法，在本文设置的算例中可将所有乘客待选时空弧由1293500条减少为530000条，节约了59.03%的搜索空间，大幅提高了搜索效率。

本算例通过通用代数建模系统(General Algebraic Modeling System,GAMS)在乘客规模为100 的数据集上进行建模和求解，实验所用计算机性能为：Intel Xeon E3-1505M v5@2.80 GHz CPU和16 GB RAM。

实验结果中某乘客具体的出行方案如表3所示。第1、第2 列给出该名乘客从出发地到达比赛场馆的路径与交通方式。后两列分别给出是否考虑出行偏好时在各点所需的出行、等待时间。对比两种不同的出行方案，可以验证引入时空等待特征系数后，乘客可以获得更为灵活、人性化的出行方案。

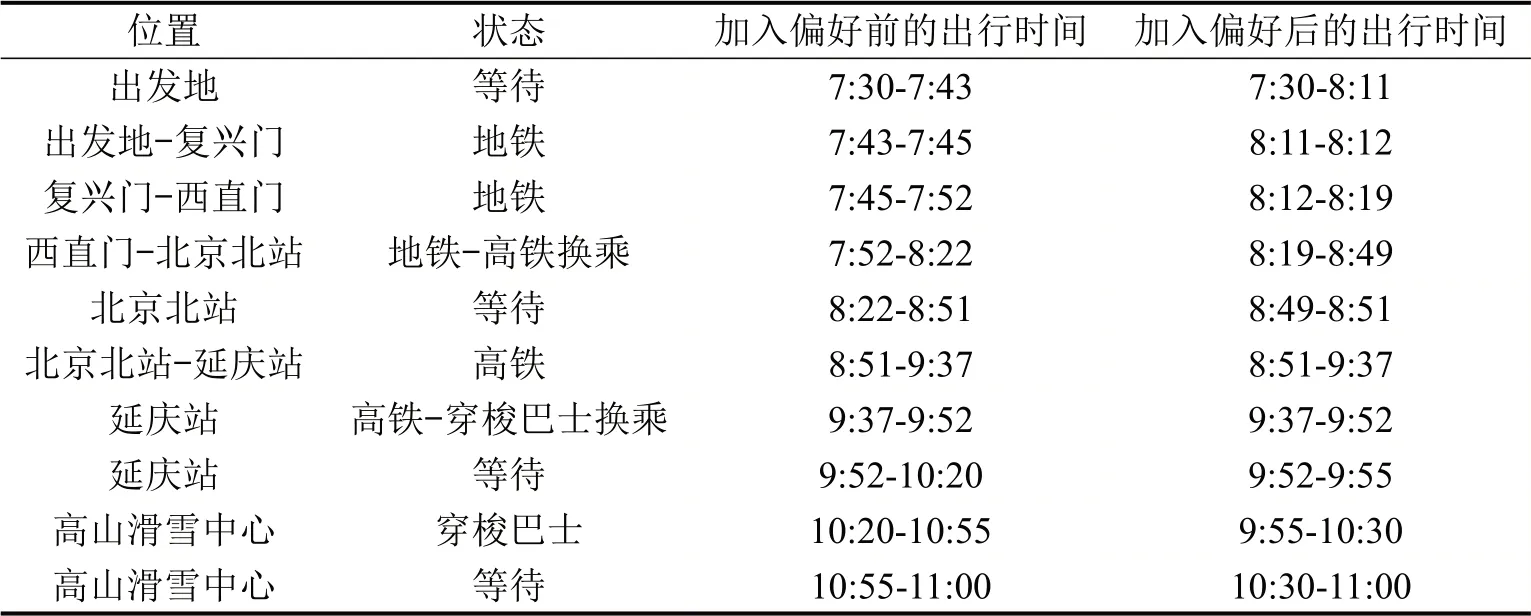
表3 观众出行时空路径列表Table 3 List of time and space paths for visitors to travel

测试过程中解的迭代过程可以进一步分析提出算法的性能。梯度优化迭代结果如图5所示。

图5 次梯度优化迭代结果Fig.5 Graph of sub-gradient optimization iteration results

图5 中精确解为通过求解器进行长时间计算所得。由图5可知，本文所提出的算法具有较好的收敛性与收敛速度，可以快速且高质量的得到一定规模观众群体的出行路径方案。

此外，为展现引入时空等待特征系数后对观众等待时间的影响，本文统计了引入时空等待特征系数前、后不同节点的人均等待时间，如表4所示。

表4 时空等待特征系数对人均等待时间影响Table 4 Influence of time-space waiting theory on average waiting time

引入时空等待特征系数后，观众更倾向于推迟出发及提前到达，以避开较为拥挤的换乘站点，因此，行程中的总等待时间由34.50 min 变为9.42 min，大幅下降。由于对观众出行路径进行了统筹规划，一定程度上缓解了公共交通的运行压力，减轻了大型活动期间交通路网的拥堵状况。

5 结论

本文提出基于时空等待特征系数的大型活动综合公共交通出行规划模型，通过数值实验得到相较于忽视出行偏好的情况，本文提出的模型得到更合理的出行路径规划方案，避免所规划的时空路径使得乘客在拥堵的地铁站和班车站点进行换乘等待。同时，通过个人的合理路径规划方案，也能减轻大型活动举办期间的路网拥堵情况。