基于自注意力机制与图自编码器的路网交通流数据修复模型

张伟斌，张蒲璘，苏子毅，孙锋

(1.南京理工大学，a.电子工程与光电技术学院，b.计算机科学与工程学院，南京210094；2.山东理工大学，交通与车辆工程学院，山东淄博255000)

0 引言

随着大量传感器的部署，人们从多种渠道收集到海量的交通数据。这些数据往往“真假共存”，存在缺失、错误、冗余等异常现象。传感器数据是数据分类、回归预测、交通信号控制优化等任务的基础，数据的缺失会影响后续的算法性能，因此需要智能交通系统(ITS)尽可能准确地修复缺失数据，提高数据完整度。交通数据修复问题有其固有的特殊性，需要考虑空间路网拓扑结构和数据随时间变化的规律性和突变性[1]，故针对交通流数据修复问题需要设计适合交通流特征的模型。

数据修复需要设计合适的算法从多维数据中提取变化规律，挖掘出数据间的相互依赖关系。传统数据修复方法存在局限性，对数据有较强的前提假设，如线性[2]，平滑[3]等。近年来深度神经网络被应用于交通流数据修复、预测等问题，取得了良好的效果。有学者从时间序列的长短时依赖关系出发，利用序列化模型对缺失数据进行修复。Berglund 等[4]提出了双向循环神经网络修复模型。序列化的模型虽然可以有效学习到时间序列的长短时依赖关系，但通常难以同时捕获时空关联性。Vaswani 等[5]提出的Transformer 模型在自然语言处理问题上取得较好的效果，Self-Attention机制也随之应用在缺失数据填补问题。上述模型虽然可以对道路交通流数据进行有效地修复，但均仅对某条道路进行时间序列分析，无法应用于较大范围的城市路网中。

随着图卷积神经网络的发展，一些学者将其应用在交通流数据预测中，并取得了良好效果。研究表明，通过GCN将路网信息嵌入到交通流预测模型中可以提高预测准确率。Wang等[6]提出的STGNN(Spatial-temporal Graph Convolutional Networks)模型将路网结构嵌入到模型中，并将S-GNN层加入到GRU(Gated Recurrent Units)的状态更新中，明显提高了模型预测准确率。自编码器作为一种端对端模型在数据修复中也取得良好效果。Zhang等[7]发现，图神经网络会使节点之间的信息产生较多的共享，导致节点特征丢失。因此，将GCN直接应用于数据修复模型中会降低修复效果。

本文针对路网交通流数据修复问题提出一种基于多头注意力机制和图卷积网络的修复模型。该模型采用自编码器结构，其中所提出的时空图卷积网络(Spatial-Temporal Graph Convolutional Networks,STGCN)可以学习路网拓扑结构，捕获数据中潜在的时空关联性。与传统GCN 不同的是，STGCN通过计算道路自注意力和一阶相邻道路注意力值构成道路权重矩阵，代替传统GCN 中的邻接矩阵。STGCN使用LSTM网络捕获数据中的时序规律，将处理后的数据代替GCN 中的图信号加入模型计算。此外，模型加入了Multihead-Attention 层捕获STGCN 难以利用的数据特征，即二阶及高阶邻接道路的空间关联性；位于缺失时刻后的数据与缺失数据的时间关联性，起到对STGCN 层的补充作用。Multihead-Attention 层以残差链的形式加入模型，可以使模型更快收敛。最后使用全连接网络输出修复结果。本文方法在实际数据集中进行验证，实验表明，该模型较一些常用模型取得了更好的修复效果。

1 问题定义

路网结构可视为一个以双向道路为节点的拓扑图结构。该图可定义为，其中，V为城市N条双向路路段的节点集合，为编号为N的双向路路段。ε为边的集合，连接着图中的N个节点。这些节点的连接关系用一个邻接矩阵来表示，其中，表示路段vi和vj的连接关系，i,j为矩阵的行列号，同时也表示道路的编号。如果vi和vj相邻，则为1，否则为0，由此邻接矩阵A为对称矩阵。将交通流数据视为在该图上的时间图信号序列，如在t时刻道路i交通流数据vi,t视为节点vi在t时刻的信号值，在t时刻城市路网交通流数据视为图信号。假设节点的个数和邻接关系不变，城市的交通流数据可以表示为图信号序列，如图1所示，其中，tn为观测时刻，为tn时刻城市的交通流数据。

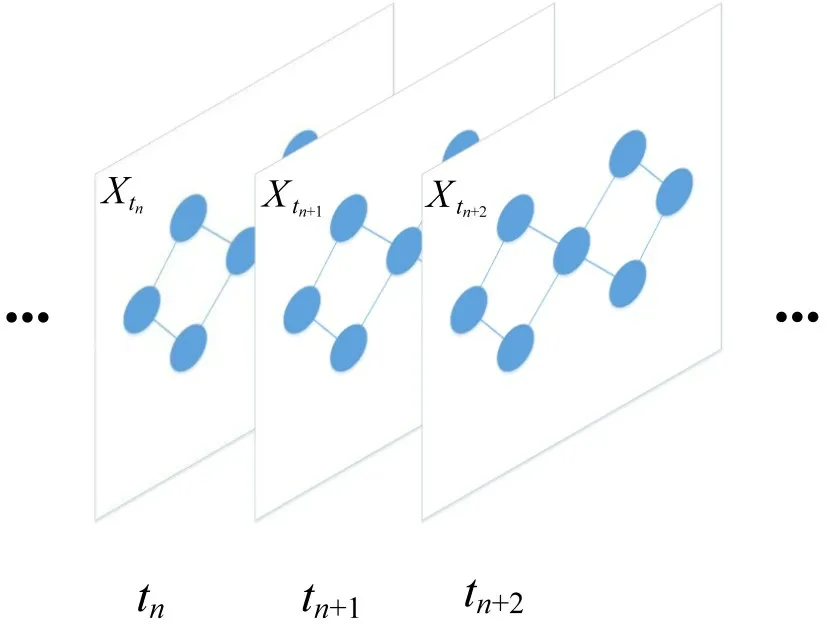
图1 城市路网交通流数据的图信号序列示意图Fig.1 Schematic diagram of graph signal sequence of urban road network traffic flow data

2 模型构建

图2 为本文模型结构。模型主要包括两个部分：①STGCN 利用LSTM 网络、注意力网络、GCN网络结合图信号和邻接矩阵，对交通流数据的时空关系进行捕捉和提取，并填补缺失部分；②由Multihead-Attention直接学习交通流数据中的特征关系。值得注意的是Multihead-Attention 相比于STGCN，结构更加简单，可将其视为STGCN 的一条特殊残差链。

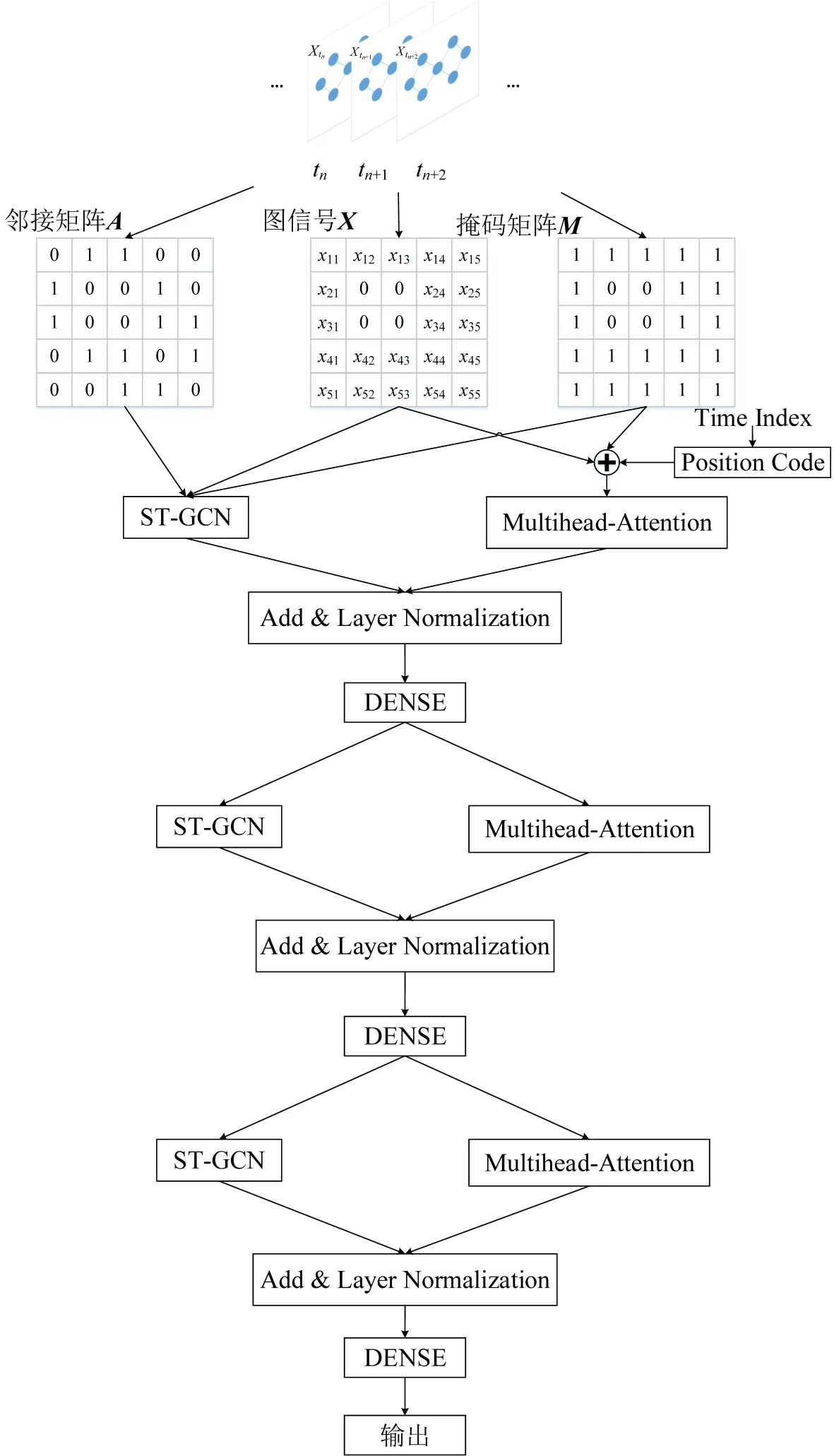
图2 模型结构图Fig.2 Model structure diagram

2.1 STGCN

路网拓扑图G(V),ε包含城市路网的道路连接信息。对于这一空间拓扑结构，模型借助Kipf 等[7]提出的GCN 捕获空间特征，对缺失路段数据使用临近路段数据填补。GCN计算过程为

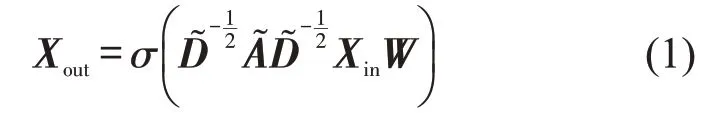
式中：σ为激活函数；为主对角线对称矩阵，，A为邻接矩阵，I为单位阵；˜为˜的度矩阵，且为节点i的一阶邻居个数之和加1，为矩阵˜对角线上的值；W为可学习参数；Xin和Xout为图信号矩阵，分别为矩阵的输入和输出。由式(1)可得出对于某个点的信号值是由其自身的信号值和其一阶相邻信号值加权求和得到，其形式如图3所示。

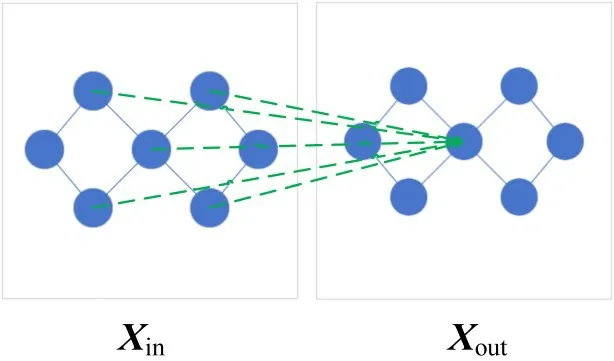
图3 GCN层映射关系Fig.3 Graph convolutional networks layer mapping

除了空间关联性，交通流数据还具有较强的时间关联性，对这一特性的提取和捕获依赖能够对时间序列建模的网络。LSTM 网络作为一种时序网络可以对数据中的时间关联性进行捕获和学习。基于GCN 和LSTM，提出STGCN 网络对交通流数据中的时空关联性进行捕获和提取，并基于提取的时空关联性填补缺失数据。网络结构如图4所示。

图4 STGCN结构图Fig.4 STGCN structure diagram

STGCN 通过LSTM 对图信号X预处理，利用数据的时序关系得到，将其传入GCN 作为图信号。值得注意的是，STGCN没有像GCN直接使用邻接矩阵，而是通过注意力网络对道路的重要性进行估算，并生成一个道路权重矩阵替代邻接矩阵。的计算过程为：先使用一层LSTM网络对图信号数据进行预处理，再通过单层注意力网络计算道路间重要性系数eij组成道路权重矩阵。预处理的作用为：对交通流数据中的时间关联性进行提取，并在缺失部分填补与历史数据有关的初始值；原始信号的表达力不够强，通过LSTM对其进行预处理，转换为表达力更强的数据输入到道路注意力网络中，使得道路注意力网络更容易地学习出道路之间的权重关系。

由道路注意力网络计算出道路间重要性系数eij组成道路权重矩阵的计算过程为

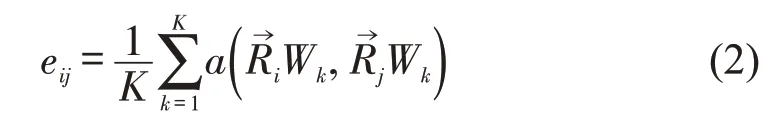
式中：a为注意力函数；K为道路注意力头数；k为注意力编号；eij为道路i与道路j的关联系数，且eij≥0。

道路注意力网络通过计算道路重要性系数，生成道路权重矩阵。将和代入式(1)，得到GCN 网络的输出。由于网络结构较为复杂，为加快模型收敛速度，使模型更容易学习到梯度下降方法，STGCN加入了残差链结构，将输入图信号与输出相加。计算过程为

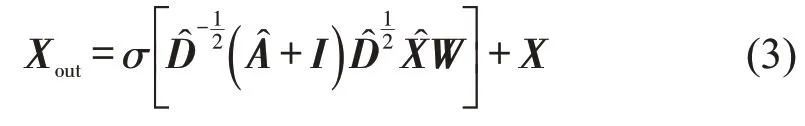
式中：σ为激活函数，实际中，模型选用Relu 作为激活函数；为由eij组成的道路权重矩阵，且沿主对角线对称；为的度矩阵，且为预处理后的图信号；X为原始输入图信号；W为可学习的参数。

2.2 Multihead-Attention

实际中每条道路的交通流数据不仅会与自身和一阶临近道路相关，与其他道路也可能存在关联性。然而STGCN仅能对每个道路自身的历史数据和一阶相邻数据关联性进行学习。除此以外，STGCN 使用的是LSTM 网络，只能利用缺失时刻前的历史数据与缺失数据的时间关系。然而在实际问题中，缺失数据常常位于数据的中间部分，即缺失前后时刻的数据都是已知的。对于这些STGCN难以捕获的特征规律，模型利用Multihead-Attention 层，通过对整个样本计算注意力权值，捕获和学习数据中所有道路所有时段之间的关系。

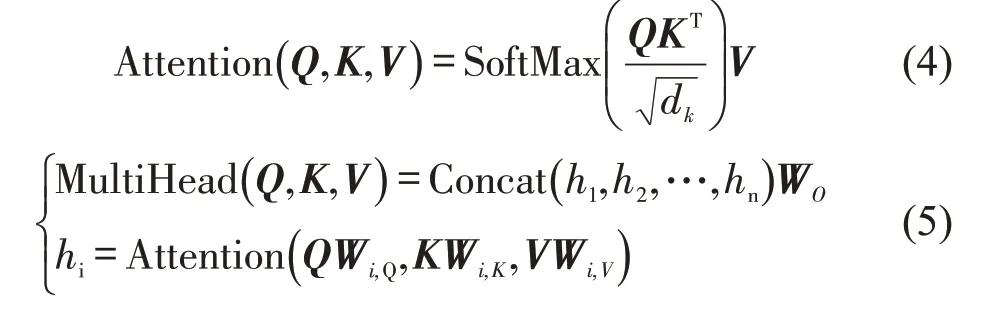
2.3 位置编码

由于注意力模块中不包含输入数据位置信息的计算，因此需要人为生成一些关于序列中标记的相对或绝对位置的信息并加入到输入数据中。受Transformer[5]的启发，使用不同频率的正弦和余弦采样值作为位置编码的信息，即

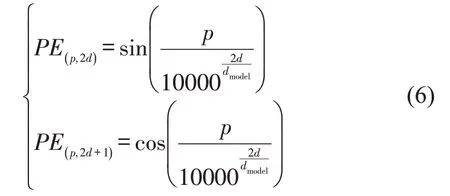
式中：p为输入数据的位置；d为维度；dmodel为输入的时间维度长度。在修复问题中，对于一天中的不同采集时刻，计算的位置编码不同。

2.4 全连接层

在每一个S-GCN 和注意力层后，加入层归一化和全连接层。层归一化能增加模型的稳定性，全连接层可对提取的特征进行整合，并给出一个响应值。因为所用数据集中本身存在缺失，将缺失值视为真实值参与训练会降低模型的修复效果，故只将有检测数值的部分代入损失函数中计算，模型的损失函数为

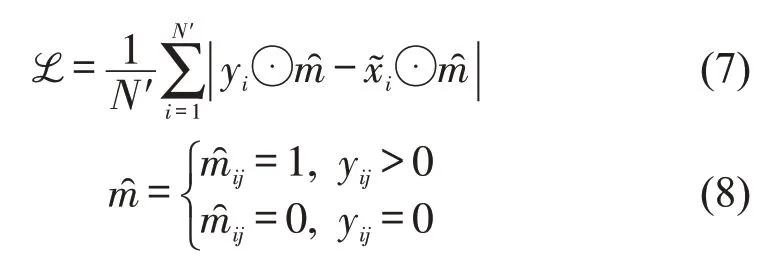
式中：y为真实数据；˜为模型输出值；N′为批大小，在实验中取N′=32；为数据矩阵中某处是否成功检测到数据，如果存在检测数据，则为1，否则为0。

2.5 模型结构总结

本文提出的STGCN网络能计算道路之间的重要性系数，并借由GCN结构重组和整合数据，以填补缺失数据。但是STGCN存在一些难以捕获的有用信息，如道路与其二阶到高阶相邻点的交通流数据关联性，缺失数据与该路段的历史数据和未来数据的关系。针对这些问题，模型采用Multihead-Attention 网络加以补充。此外，模型中每一个STGCN 和Multihead-Attention 后都加入了Layer-Normalization，确保梯度下降能传播到网络的每一层，并添加了全连接层用于信息的整合和提高收敛速度。

3 实验验证

3.1 数据集

实验部分所用数据集来自某市187 个交叉口的SCATS 运行记录解析后的真实数据，数据采集时间间隔为5 min，采集日期为2018年6月1日-8月31日。路网区域范围如图5所示，图中，白色点位是无法获取数据的交叉口，黑色点位是能够获取数据的交叉口。

图5 路网区域范围Fig.5 Road network area

以相邻两交叉口为一个路段，共得到277个路段，将各路段原始流量数据聚合为5 min 步长的等时间间隔数据。样本构造方式为在数据集上沿着空间和时间两个维度滑动截取。空间上按照道路编号顺序滑动截取每60 条道路，空间滑动步长为1。时间上滑动每截取连续的60个时间点，时间间隔为5 min，时间滑动步长为10。挑选出缺失率低于30%的样本作为实验数据集，共计324383 个样本。根据路网道路信息可得到道路之间的连接关系并构成邻接矩阵，总道路邻接矩阵的维度为(277，277)，每个样本的维度为(60，60)，样本的邻接矩阵维度为(60，60)。在实验数据集中随机选取80%作为训练集，剩余20%作为测试集。实验中模型使用Adam 优化器，学习率α=0.005，批大小Batchsize为32。

针对交通流量的缺失特点设计3种缺失模式：块状缺失，时间条状缺失和空间条状缺失。

(1)连续路段上的连续时间缺失

如图6(a)所示，数据在连续的检测线圈上发生时间上的连续缺失，造成的原因可能是路侧控制处理单元的数据传送到监控分中心的过程中发生丢失。

(2)特定时间上在采集设备上的连续缺失

如图6(b)所示，某些时刻的数据未采集，造成的原因可能是通信或者系统故障。

(3)特定采集设备在时间上的连续缺失

如图6(c)所示，某些采集线圈数据未收集，造成的原因可能是单个线圈损坏导致该路段数据未采集，或是某些路口未安装检测设备。

而二进制粒子群算法[6]，速度更新公式不变，含义有所变化。状态空间中的每一个粒子的位置xid值为0或1，选择哪个则取决于vid的大小，即速度为位置取值的概率。分两种情况：① vid较大，xid较大概率取1，较小概率取0；② vid较小，xid较大概率取0，较小概率取1。

图6 缺失模式展示Fig.6 Missing pattern

3.2 数据实验

为验证所提模型的有效性，选取4个基准模型(HA，KNN，AE，M-RNN)进行数据实验对比。

3.2.1 基准模型

仿真实验里神经网络模型均通过TensorFlow神经网络计算库搭建。各种基准模型的介绍如下：

(1)历史平均(Historical average,HA)

滑动历史平均模型使用历史交通流量的时间平均值作为填补值，进行数据修复。

(2)K-最近邻(K-nearest neighbor,KNN)

使用插值函数利用邻近k长度向量插补缺失值。在实际部署过程中，k值设置为3。

通过构建包含3 个全连接层的自编码器达到对输入数据重构的目的。每个全连接层的神经元个数为60，激活函数使用Sigmoid，并使用Adam优化算法反向传播。

(4)双向循环神经网络[8](Multi-directional Recurrent Neural,M-RNN)

M-RNN 由包括60 个神经元的双向LSTM 组成，使用Adam梯度下降算法进行网络训练。

3.2.2 评价指标

为比较不同修复模型的性能，采用MAE 和RMSE 评价修复数据和缺失处真实数据之间的偏差。

平均绝对误差(MAE)表示两矩阵平均绝对误差，公式为

平均根方误差(RMSE)表示两矩阵根均方误差，公式为

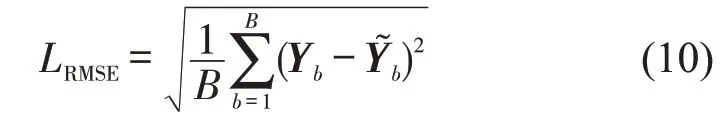
式中：Yb为缺失处真实数据；为缺失处真实数据；B为批大小Batchsize，实验中为32。

3.2.3 实验结果

根据上述模型和生成的修复数据，对各个模型的实验结果进行分析。表1～表3 为不同修复算法在3种缺失场景，以及不同数据缺失率情况下的修复表现。在绝大多数情况下，基于SA-GAE(Self-Attention Graph Auto-Encoder)的方法获得最佳的修复精度。

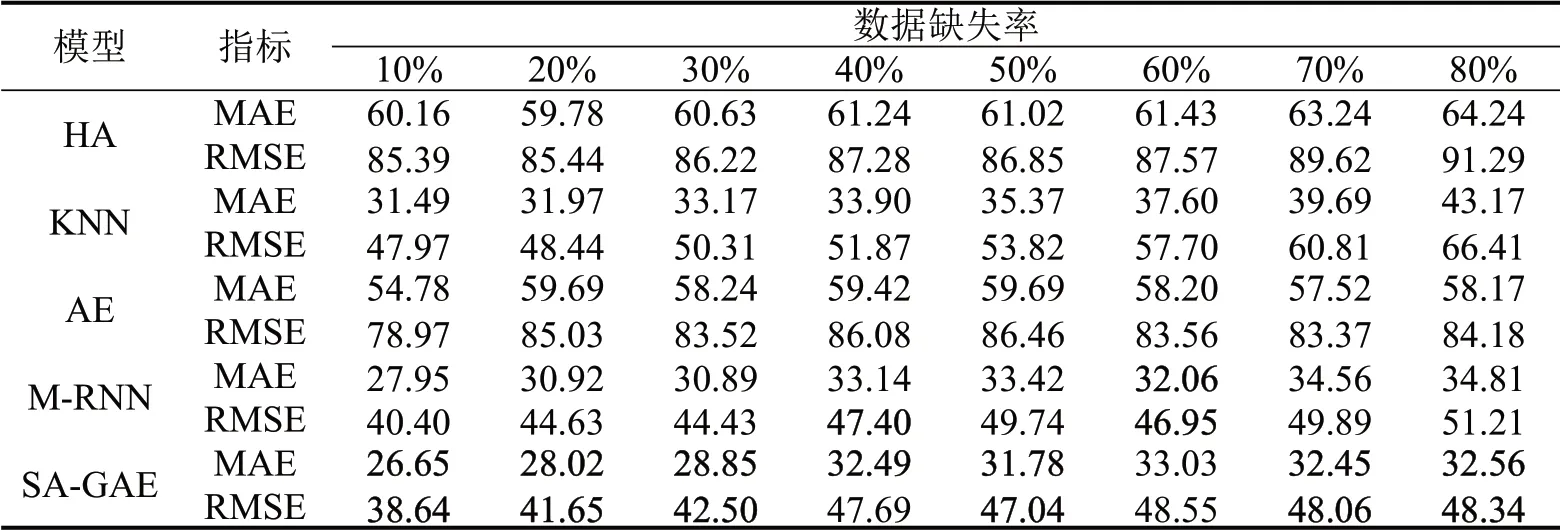
表1 场景1下的数据修复表现Table 1 Data imputation performance under scenario 1

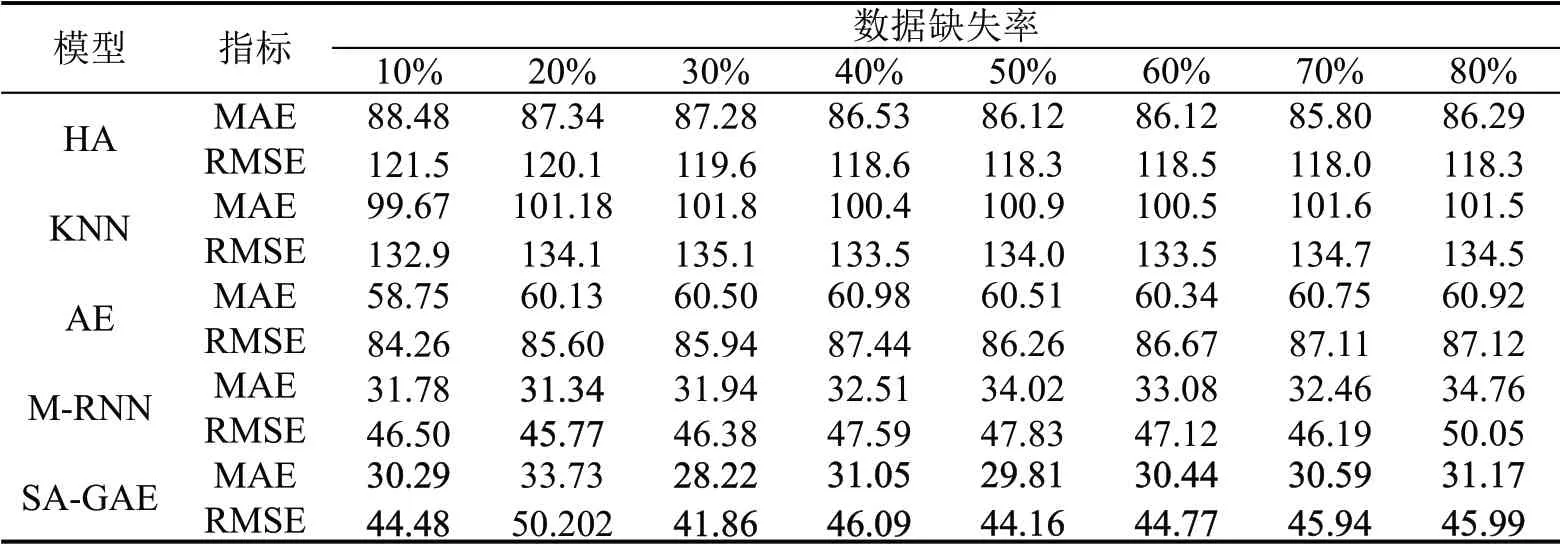
表2 场景2下的数据修复表现Table 2 Data imputation performance under scenario 2

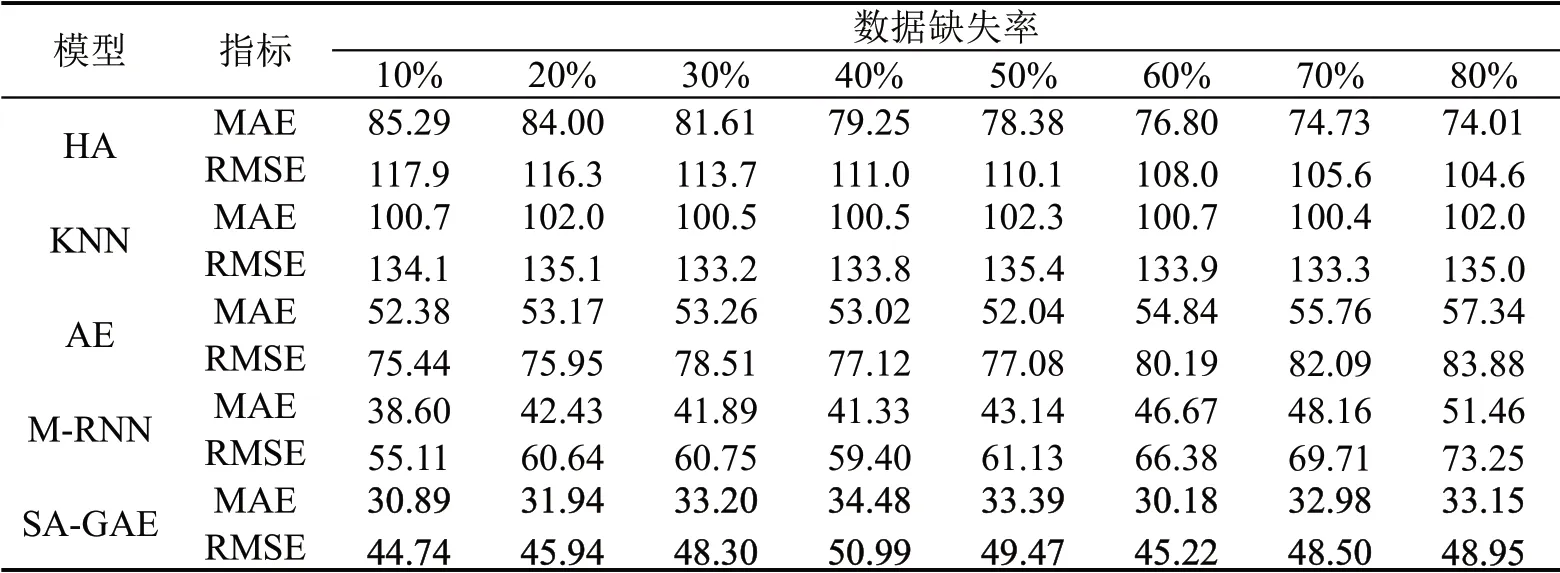
表3 场景3下的数据修复表现Table 3 Data imputation performance under scenario 3

HA 和统计学模型KNN 方法没有考虑交通数据的突变性及路网拓扑图结构关系，不能对交通数据的时间关联性加以利用，产生的修复值可靠性不强，与缺失部分的真实值关联度较低，因此修复结果不佳。

自编码器方法能够对数据中的关联性进行学习和捕获，取得了一定的修复效果，但是缺少对交通流数据特性的针对性设计，并且无法学习空间路网拓扑图结构，故修复效果难以进一步的提高。M-RNN 由于可对时间序列建模，在缺失模式1，2下取得了不错的效果；但是在缺失模式3 下，由于其无法利用空间路网拓扑图结构，不能捕获缺失道路与其临近道路数据之间的关系，难以有效修复缺失数据。

本文提出的SA-GAE 模型不仅可以对数据中的时空关联性进行学习，还能利用空间路网拓扑图结构进一步提高修复效果。通过ST-GCN 网络捕获路网数据中蕴含的时间规律，并利用拓扑图结构学习一阶相邻道路数据中的空间关联性。对于STGCN难以捕获的残余关联性，本文使用Multihead-Attention 进行学习并以残差链的形式加入到网络中，最终达到精确修复缺失数据的目的，在多种缺失模式下取得最优效果。以图7为修复示例，其为SA-GAE 模型在缺失模式2 下，缺失率为50%时的修复结果，其中第1行为输入的缺失数据，第2行为模型输出的修复结果，第3行为对应的真实完整数据。通过式(9)和式(10)对图7中缺失部分的修复值与真实值计算误差，MAE 为29.81，RMSE 为44.16。与自编码器相比，相同缺失率下MAE 下降了30.70，RMSE 下降了42.10；与M-RNN 相比，MAE下降了4.21，RMSE下降了3.67。

图7 SA-GAE修复结果示意图Fig.7 Schematic diagram of SA-GAE repair results

4 结论

本文针对路网交通流数据修复问题，提出一种基于多头注意力机制和图卷积网络的数据修复模型SA-GAE。与其他修复模型相比，该模型可以学习城市路网拓扑结构，捕获交通流数据中的时空规律，并基于捕获到的时空规律对缺失数据进行有效修复。并且，该模型能够应用于复杂城市路网结构多种缺失情景下的数据修复问题。真实城市路网交通流数据实验结果表明，该模型相比常用的修复模型在多种缺失率和缺失场景下均取得了较好的修复效果。