GFE 变速器输入轴热处理的工艺参数优化

姚振鑫，宋新萍，苏宁

（201620 上海市 上海工程技术大学 机械与汽车工程学院）

0 引言

GFE 输入轴生产工艺质量直接影响着发动机动力传输的精度及效率。热处理作为GFE 输入轴后续加工成型的重要工艺，在强化金属材料、展现材料潜在性能、保证零件具有优良机械性能等方面起到非常关键的作用。但在热处理过程中易发生变形，由于零件发生的变形过大，通过加工精磨难以消除变形，必须重新加工制作新的零件，导致材料在输入轴生产过程中的利用率降低，增加了零件的生产成本，而且变形的零件也难以满足使用过程中的机械性能要求，如何将热处理过程中进行参数优化在一个合理的范围成为科研的关键点。

1 热处理工艺对工件的影响

在热处理过程中，工件在加热和冷却这2 个过程中更容易发生变形，下面主要分析加热过程和冷却过程中工艺参数对变形的影响[1]。

（1）加热的不均匀性对变形的影响。不均匀加热并不是指加热过程中工件表面和心部由于升温速度不同而产生的温度差，而是指由于其他原因致使工件无法保持各向同性而出现温度梯度的现象。对于结构复杂或者导热性能差的工件，一般加热速度较为缓慢或在热处理前预热以减小热处理引起的变形[2-3]。

（2）加热温度对变形的影响。加热温度通过改变淬火冷却时的温差、淬透性、Ms（马氏体转变的起始温度）点对热处理变形产生影响。淬火温度升高，组织开始向奥氏体转化，Ms 点也随之变小，此时因相变产生的组织应力对变形的影响减小，在套类工件实际热处理中的孔腔更容易收缩。

（3）冷却速度对变形的影响。在冷却过程中，不同冷却介质决定了冷却速度不同，同时，对变形的影响复杂多变，但原则是淬火冷却速度大小更倾向于保证要求的组织和性能[4-5]。

2 试验材料及热处理生产工艺

为了获得用于BP 神经网络算法优化的训练样本和测试样本，需要对输入轴进行多组热处理试验，本文通过对输入轴试样成分和结构分析，结合输入轴热处理实际生产情况，确定出输入轴热处理工艺。

2.1 试样成分

本文中选用的钢种为20CrMnTi。20CrMnTi作为渗碳热处理用钢，钢中含有Cr，Mn，Ti，其在保证较高淬透性的同时，具有较高的强度、韧性和良好的抗疲劳性能，可作为齿轮、轴类和活塞类零配件，用于汽车中的特殊结构部位[6-7]。

将材料切割成15 mm×15 mm×10 mm 和25 mm×25 mm×10 mm 的方块，15 mm×15 mm× 10 mm的方块进行化学分析，测出C，Cr，Mn，Si，Ni，元素成分，对25 mm×25 mm×10 mm 进行荧光光谱分析，测量其剩余元素的含量，得出试验材料的成分见表1。

表1 20CrMnTi 成分表Tab.1 20CrMnTi ingredients

GFE 变速器输入轴材料中元素含量对热处理过程中组织转变的速度有影响，同时,能够提高材料的淬透性，使工件更容易淬火[8]。

2.2 试样结构

GFE 变速器输入轴结构如图1 所示。

图1 输入轴三维模型Fig.1 3D model of input axis

图1 中，GFE 输入轴为空心结构，长度271.7 8mm，内孔小径 15 mm，内孔大径 21 mm，外圆小径 22 mm，外圆大径 27.4 mm，小端花键的齿数20，模数1.5，大端花键的齿数30，模数0.75。通过该输入轴的长径比，得出输入轴为长轴类零件。

2.3 热处理生产工艺

根据输入轴的技术要求，热处理的生产工艺为：高温渗碳——淬火——低温回火。碳势的高低影响渗碳的快慢。高温渗碳时，需要将碳势升高到0.75%～1%，增加渗碳效率，降低成本。如图2 所示，高温渗碳的过程为：装炉——加热到650 ℃，保温1 h；继续加热到850 ℃，保温1 h；再加热到910～930 ℃，保温2 h；降温到840～860 ℃，保温一段时间为淬火做准备。

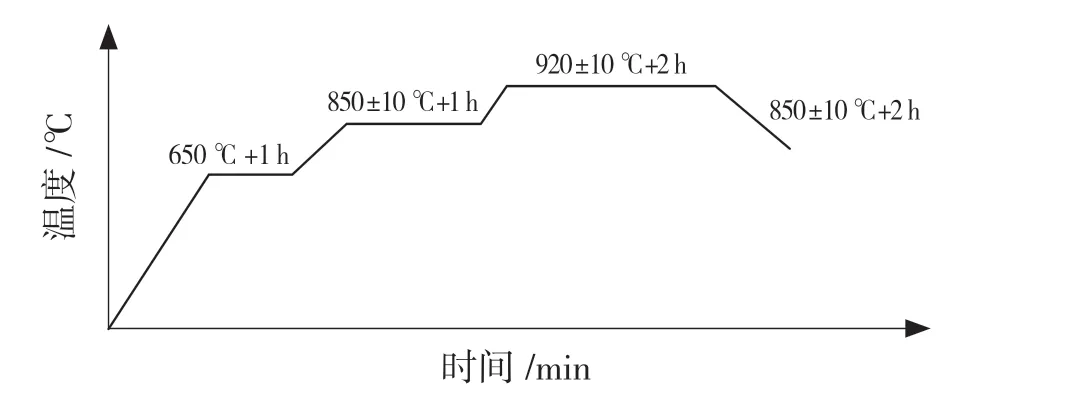
图2 高温渗碳热处理流程图Fig.2 High temperature carburizing heat treatment flow chart

如图3 所示，淬火过程为：气体渗碳后，工件采用渗碳温度随炉温降温到适宜的淬火温度，经过一段时间的保温后，直接开始淬火，将温度保持在840±10 ℃保温2 h，然后冷却。

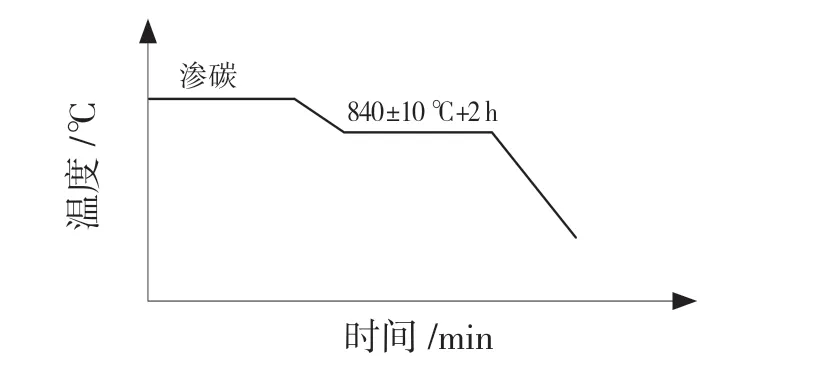
图3 淬火流程图Fig.3 Quenching flowchart

如图4 所示，回火过程为：工件淬火后，在电阻炉低温回火，采用到温加热的方式，可减少加热的时间，即加热到190±10 ℃将工件放入电阻炉，然后出炉空冷。

图4 回火流程图Fig.4 Tempering flowchart

上述热处理生产工艺中，工件在渗碳、淬火、回火阶段时间一般并非完全固定，通常时间控制在一定范围几乎不会对变形产生影响，温度则依据材料的铁碳平衡图结合以往热处理经验验证得到[9-10]，但精确度较低，对热处理后的工件变形有较大影响。

3 试验方法

正交试验法可以有效规避不具代表性的试验，甄选出的试验方案得出的试验数据可以作为BP 算法优化的训练样本和测试样本[11]。本文选用混合水平正交表L25（52×41），选取渗碳温度、淬火温度、冷却方式和回火温度4 种工艺参数进行优化研究，将冷却的方式分为：油冷、水冷、炉冷、空冷分别对应记号为1，2，3，4，这样可以方便进行数据的拟合处理。表2、表3 分别表示正交试验因素水平表和正交试验方案。

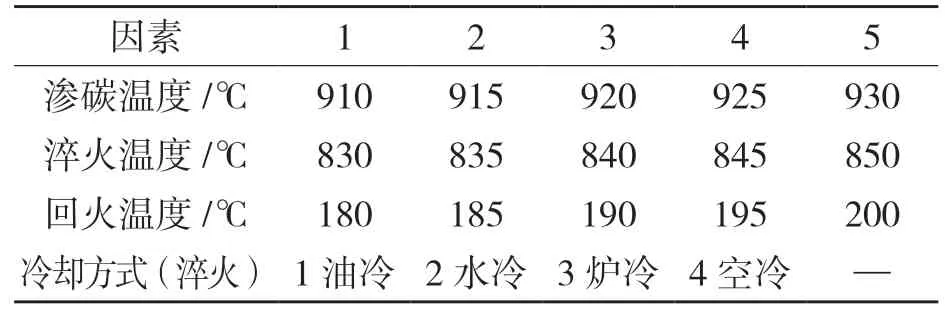
表2 正交试验因素水平表Tab.2 Levels of orthogonal test factors

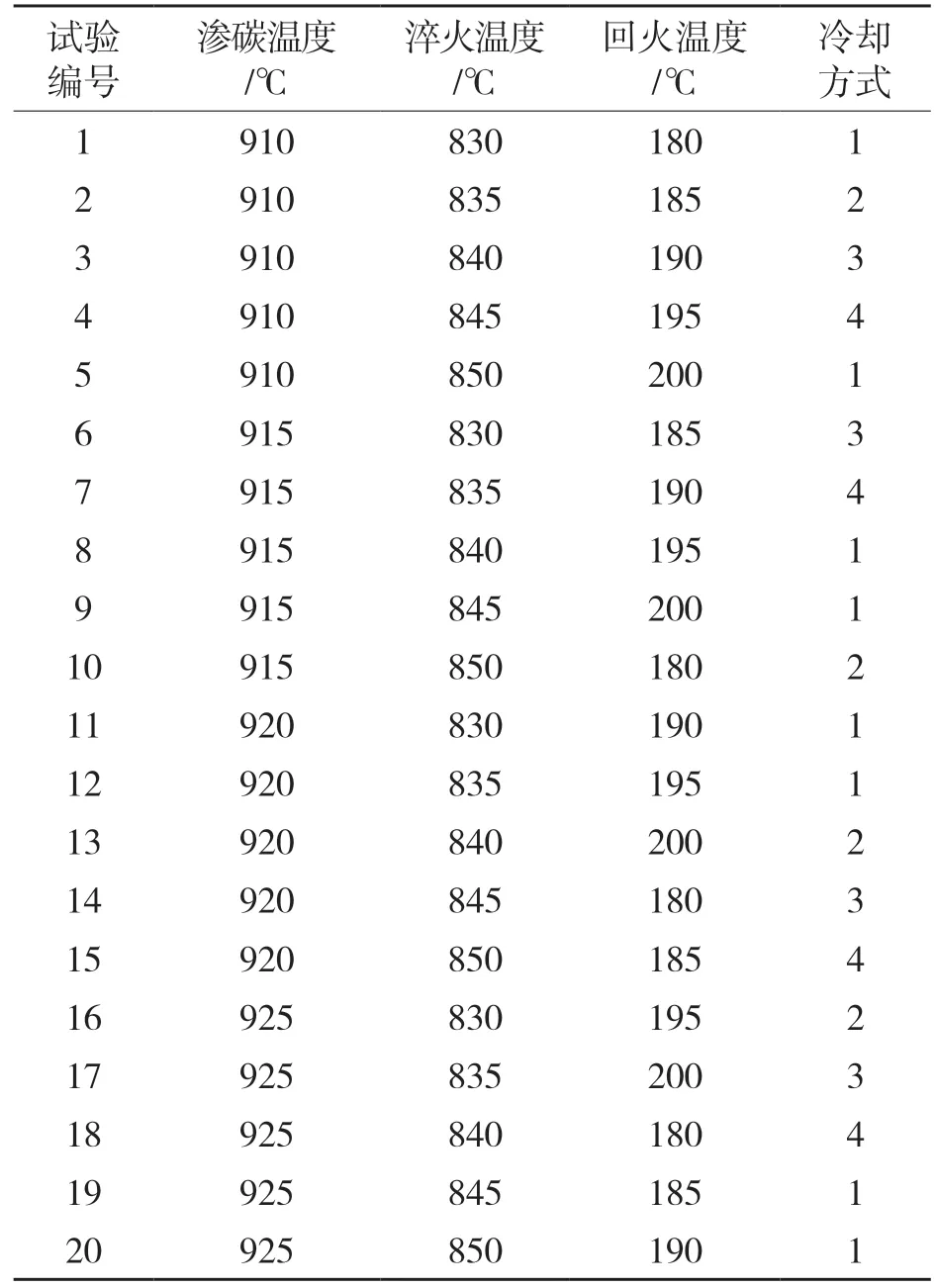
表3 正交试验方案Tab.3 Orthogonal test scheme

选取工件重要位置如图5 所示，分别标记为a，b，c，d，e，f，并测量出该处实际直径与理论直径的变化量。试样工件根据表3 的试验方案，测量出热处理后的工件相同位置的直径变化量。输入轴热处理前后直径的变化量如表4 所示。

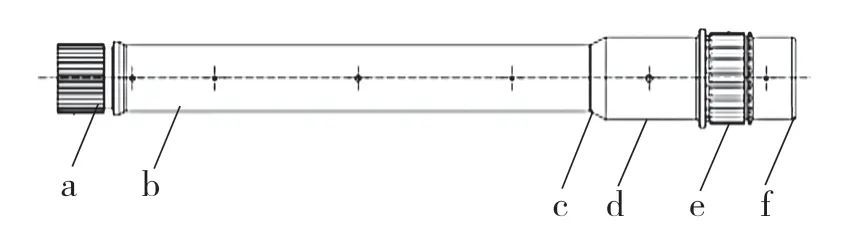
图5 试样工件示意图Fig.5 Sample workpiece schematic

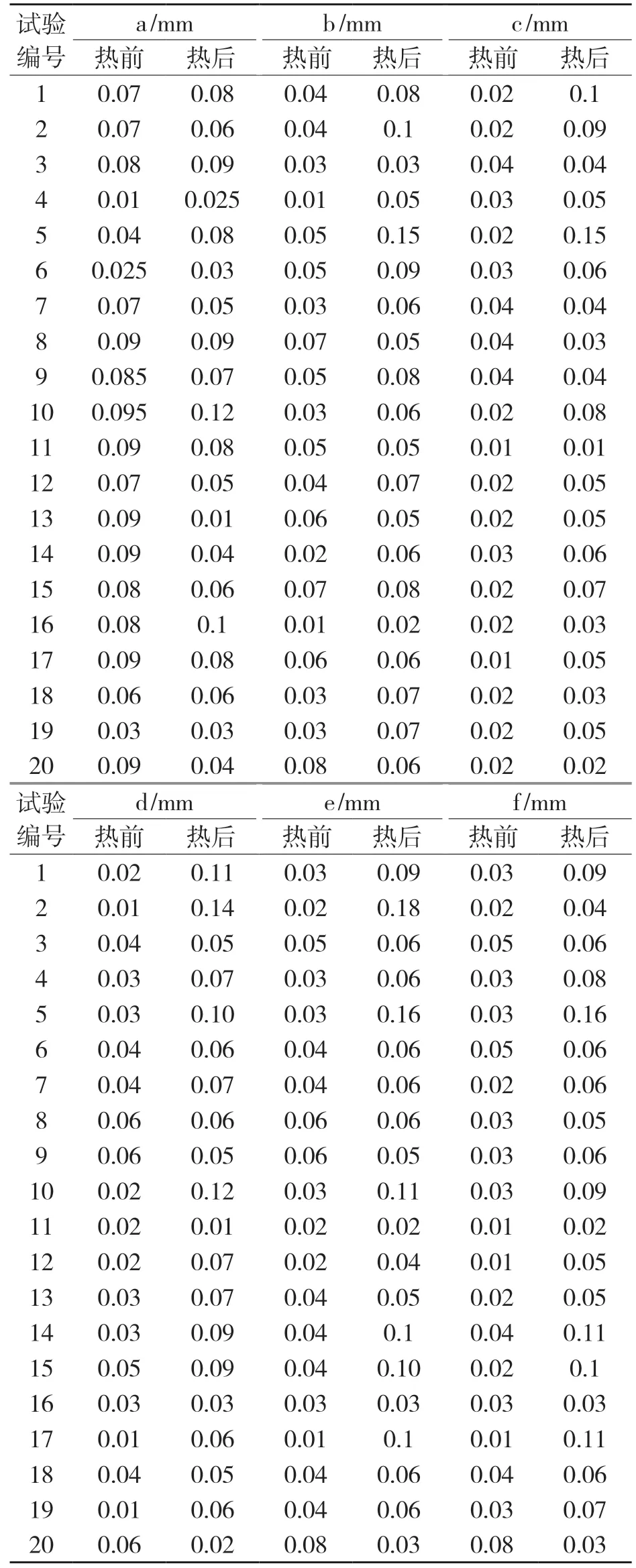
表4 热处理前后直径变化量对照表Tab.4 Comparison of diameter changes before and after heat treatment

表中a，b，c，d，e，f 列GFE 输入轴热处理前直径变化量与热处理后直径变化量取差值，并根据试验序号作折线图，比较输入轴a，b，c，d，e，f 位置处热处理前后直径变化量变动的大小。

分析图6，图6（a）中，输入轴热处理前后直径变化量差值在[-0.1，0.05]波动；图6（b）中，输入轴热处理前后直径变化量差值在[-0.05，0.1]波动；图6（c）中，输入轴热处理前后直径变化量差值在[-0.1，0.15]波动；图6（d）中，输入轴热处理前后直径变化量差值在[-0.05，0.15]波动；图6（e）中，输入轴热处理前后直径变化量差值在[-0.1，0.2]波动；图6（f）中，输入轴热处理前后直径变化量差值在[-0.1，0.15]波动。根据实际的热处理技术要求，输入轴热处理前后直径变化量超过0.1 mm 需要进行校直。图6（e）中，输入轴热处理前后直径变化量差值波动范围较大，且差值接近0.1 mm 的试验组数较多，因此，选择输入轴e 位置处的热处理前后直径变化量差值作为优化目标，优化热处理工艺参数。

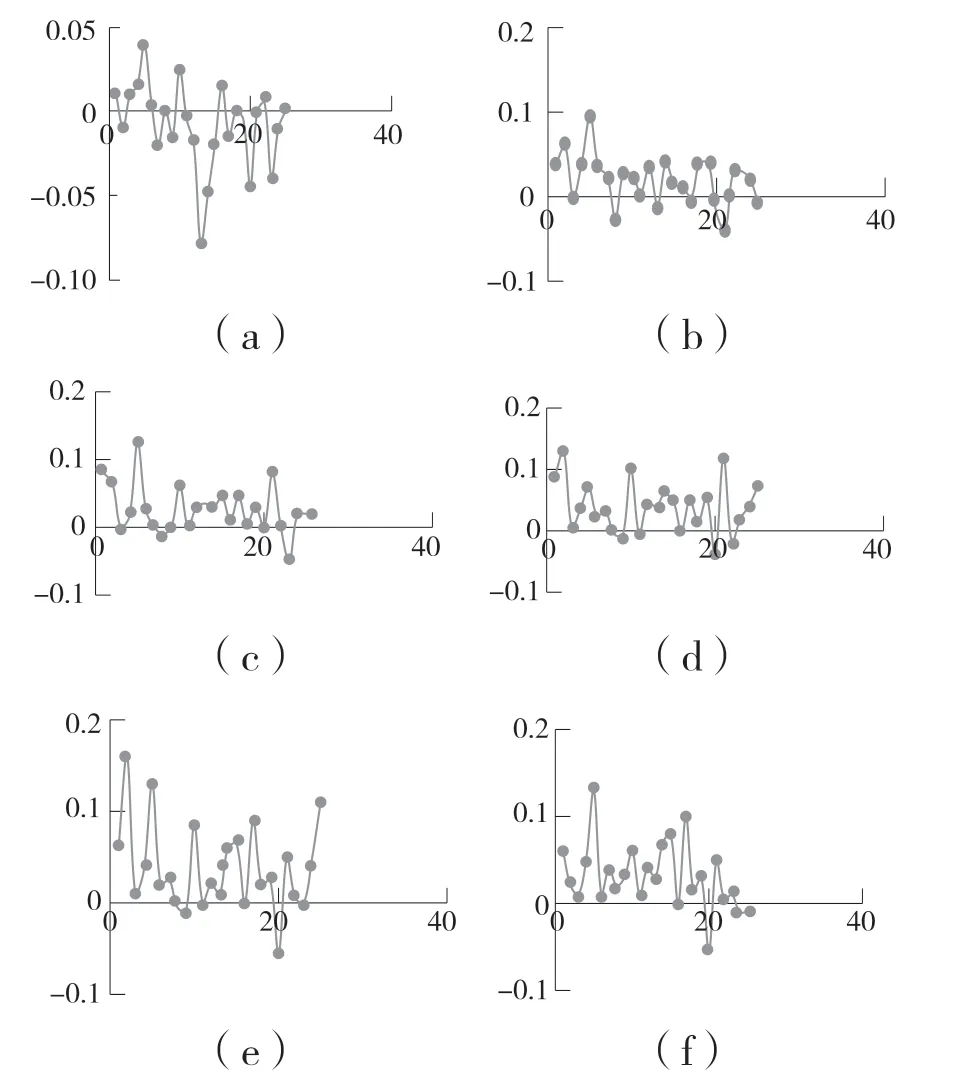
图6 试样工件标记位置热处理前后直径变化量差值Fig.6 Difference in diameter change before and after heat treatment

4 BP 神经网络优化模型的构建和训练及预测

BP 神经网络是一种基于深度学习的预测方法，可以对无规律的数据进行训练，得出数据之间的内在映射关系，通过误差逆传，实现模型的精确训练，可直接根据已有的试验数据建立可靠的数学模型，以及预测数据的变化趋势[12]。

4.1 神经网络模型的构建

本文采用3 层网络结构，以渗碳温度、淬火温度、冷却方式和回火温度作为网络的输入，以输入轴热处理前后直径变化量差值作为网络的输出，则输入层节点数m=4，输出层节点数n=1，隐含层节点数h 的取值通常采用经验公式其中，α一般取1～10 的常数，确定隐含层节点数的基本原则是当预测精确度得以控制时，一般取得隐含节点数越小越好，由于隐含层节点数一般大于输入层节点数。因此，确定隐含层节点数h=5，则BP 神经网络的结构为4-5-1。

4.2 神经网络模型的训练及预测

选取表4 中e 列输入轴热处理前后直径变化量差值的20 组作为训练样本，其余5 组作为测试样本。由于各工艺参数间的大小存在很大的差异，为了保证模型的正常训练，对数据进行归一化处理，将样本数据转化为[0.1，0.9]区域内，将处理的数据输入到网络中进行训练，网络训练以激励函数中的双曲正切函数tansing 作为输入层到隐含层之间的传递函数，隐含层到输出层采用函数purelin，训练算法采用Traingdm 算法，学习速率为0.1，训练误差为0.001。得出该模型训练的性能曲线如图7 所示。

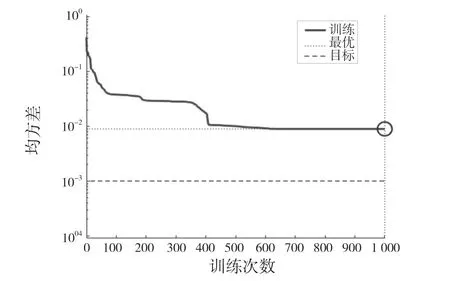
图7 模型的训练性能曲线Fig.7 Model training performance curve

从图7 中可以直观地看出，经过700 次训练后，其性能曲线起伏较小，趋近平滑，证明该模型拥有较好的稳定性，更能明显反映出输入参数（渗碳温度、淬火温度、冷却方式和回火温度）与输出参数（输入轴热处理前后直径变化量差值）之间的关联。

训练好的神经网络模型，在优化热处理工艺参数之前，要对其准确性进行验证，从而保证预测精度。表4 中e 列，输入轴热处理前后直径变化量差值剩余5 组未经训练的试验数据作为测试样本，将这些样本重新编号为1，2，3，4，5，并且代入模型中进行测试。测试所得理论值与热处理试验值对比如图8 所示，理论值与试验值相对误差如图9 所示。

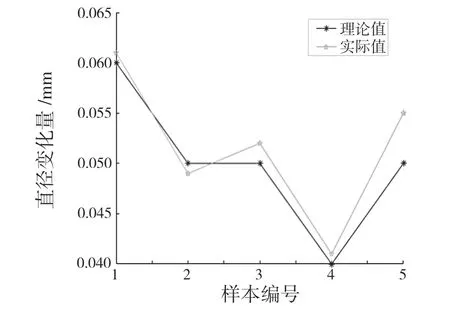
图8 模型的预测验证结果Fig.8 Verification results of model prediction

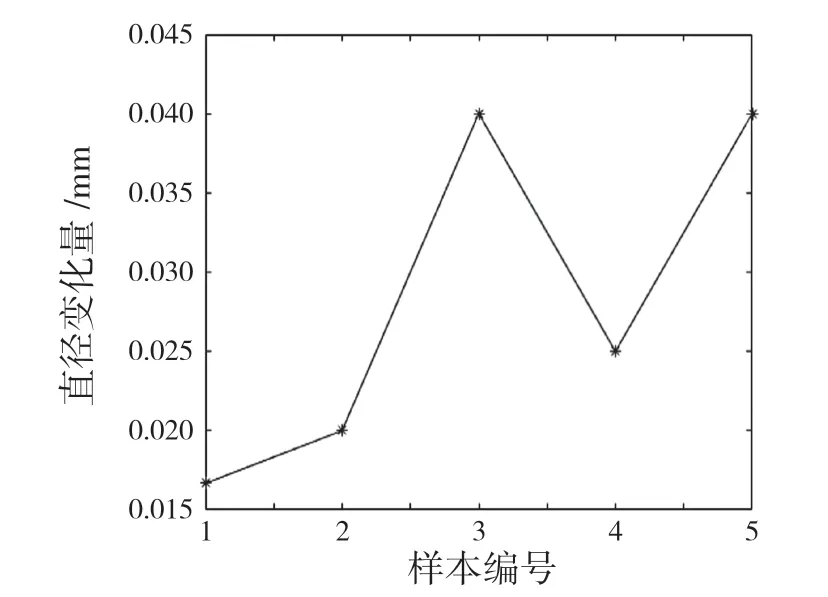
图9 理论值与试验值相误差Fig.9 Error between theoretical value and experimental value

从图8 和图9 可以看出，该模型预测的结果与试验值相接近，相对误差值较小，其相对误差范围为0.015～0.045，因此，该模型不但拥有较强的预测能力，而且预测精度也较高，能够客观地反映输入参数与输出参数之间的关系，可用于预测。

5 遗传算法的全局寻优设计

遗传算法（Genetic Algorithm）借鉴了生物界的优胜劣汰的进化规律而演化出的全局寻优方法，这种方法的核心是自然选择和遗传，通过自然选择、遗传、交叉来寻找群体中的最优解[13]。本文以渗碳温度、淬火温度、冷却方式和回火温度4 种热处理工艺参数作为设计变量，根据已经建立的BP 神经网络模型，利用遗传算法的全局寻优功能，对上述热处理工艺参数进行优化，优化模型可表示为

设计变量：X=[T1，T2，T3，p]

目标函数值：Y

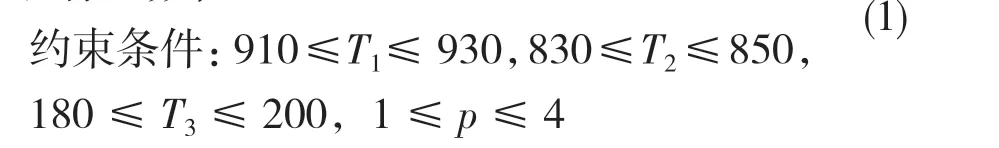
式中：Y，T1，T2，T3，p——输入轴热处理前后直径变化量差值、渗碳温度、淬火温度、退火温度、冷却方式。

5.1 遗传算法的实现过程

生成初始种群。初始种群的确定包括种群的大小和种群中个体产生方式的确定。表3 渗碳温度、淬火温度、冷却方式和回火温度4 种热处理工艺参数的取值范围，随机生成50 个个体作为初始种群。

（1）目标函数和适度函数的确定

将遗传算法随机产生的个体作为神经网络模型的输入，模型输出的预测值作为遗传算法的函数目标数值，即

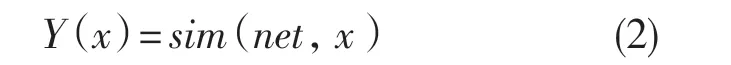
式中：net——构建好的神经网络模型；sim——仿真函数；x——网络的输入；Y——目标值。

遗传算法的适应度函数用来衡量群体中个体的优劣，其直接影响算法的收敛速度和能否找到最优解。由于本文应求出输入轴热处理前后直径变化量差值的最小值，所以可将目标函数作为适度函数。

（2）遗传算子。以适度函数为根据进行选择。将适应度高的个体保留，淘汰适应度低的个体，使个体不断接近最优解。交叉是将已选择的个体部分结构进行重组，个体发生交叉过后，能够显著提高遗传算法的运算速度和精确度。变异是改变个体中的某个基因，从而形成新的个体。本文在选择算子上采用随机遍历抽样法，交叉算子则采用多点交叉，交叉概率，变异概率Pm=0.06 确定最大的遗传代数为200。

5.2 全局寻优结果

通过遗传算法全局寻优，经200 代遗传进化得出输入轴e 位置热处理前后直径变化量最优差值，并且找到了输入轴热处理工艺参数的最优化配置，结果分别为：

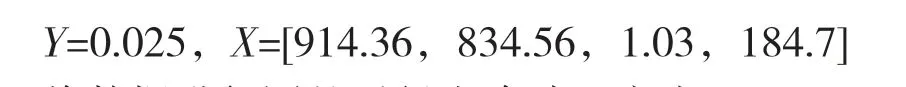
将数据进行圆整后得出渗碳温度为915 ℃，淬火温度为844 ℃，冷却方式为油冷，回火温度为185 ℃。

6 结论

本文运用BP 神经网络算法和遗传算法对输入轴热处理工艺参数进行优化，进而控制热处理变形。该方法具有一定的代表性，在实际的热处理生产过程中，不同类型的工件都可以运用该方法优化影响变形的主要工艺参数。本次研究采用的是BP 神经网络和遗传算法结合的优化方法，由于算法自身的局限性和优化的工艺参数较少，可能会造成控制热处理变形的效果未达到最优化。如果能充分考虑热处理变形的影响因素，优化更多工艺参数便能够为热处理变形控制提供更为准确的指导。