亲属关系自动推理模型研究

李彩玲 刘俊

(1.临汾职业技术学院计算机系，山西 临汾 041000；2.北京神舟航天软件技术有限公司，北京 100094）

1 引言

亲属关系在户籍管理、公安案件侦查、知识图谱等领域均有着重要的应用价值。亲属关系在计算机大规模应用之前就有应用，因此，要通过计算机分析处理亲属关系，需要设计恰当的计算机表示方法。

以户籍制度为例，新中国成立之初便开始了户籍制度的建设，户籍信息中很重要的一个部分就是户籍下属的人与户主的亲属关系。经过多年的发展，户籍数据已经很大程度上实现了电子化。由于这些亲属关系的数据目前还是以传统的关系数据库存储，户口登记只记录了户籍下的个人同户主的关系，而户籍下两个个人之间的关系则是缺失的，需要根据已有的关系进行推理产生。亲属关系数据要应用在案件侦查、知识图谱领域，必然面临亲属关系数据需要通过推理补全的情况。

陈振宇[1]等人设计了用于中文的亲属关系逻辑表达模型及其推理方法，以“自己、母、夫、父、妻、子、女、兄、弟、姐、妹”这11种关系为基本关系，定义了其他的常用关系。而后设计了相应的推理系统，对于已知的关系集合S，首先将S中的所有关系全都按照定义转化成前述11种基本关系表达的形式，然后对能够连接的关系进行连接，最后通过预定义的含有14322 条规则的数据库，把关系表达式还原成常用的亲属关系输出。这一方法的缺陷在于逻辑谓词的计算实际上会有大量的冗余计算，同时需要手工编写的规则数量是比较大的且难以证明其完备性。

黄锐[2]基于本体概念构建了亲属关系的知识模型，涵盖了简单的亲属关系；同时加入了SWRL规则用于推理出亲属间的隐藏关系。这一方法引入了本体表示模型，在亲属关系的知识表示上有推动作用，但是其本质仍然是一个基于规则的系统。

卢达威[3]等人论述了亲属称谓系统的复杂性和亲属推理的边界等问题，指出一个亲属推理系统并非要表示所有的亲属关系，但是应该有形式化的定义，明确亲属推理系统的表示范围。卢达威利用婚姻关系、生育关系、被生育关系、兄弟姐妹关系作为四个基本血缘关系，重新设计了亲属关系表达式。通过在血缘关系结构图上寻找两个与同一个人有亲属关系的人之间的最短的亲属关系路径的方法进行亲属关系推理。其特点在于将图结构引入了亲属关系的表示，利用图中的路径表示亲属关系，有很大的借鉴意义。其问题在于某些条件下亲属关系无法唯一确定的情况，比如表妹的母亲和我本人的关系就是一个无法唯一确定的例子。

John H.Winkelman[4]论述了四种亲属关系的表示系统，分别是关联系统、语义特征系统、逻辑谓词系统和基于集合映射的代数系统。使用关联系统和语义特征系统表示亲属关系不能够满足实际要求；基于逻辑谓词的系统因其解决问题并非按照人类思考的方式，往往缺乏有效的方式将多种关系进行合并，计算复杂；基于代数的系统由于符合人类思考过程、简洁等优点受到John H.Winkelman的推崇。

总体而言，相关的研究较少，主要使用了基于逻辑谓词、本体等的关系表示模型；此外中文语境下的亲属关系与英文语境下还有些许不同，英文的研究成果无法直接应用于中文环境。因此，对该问题进行进一步的研究具有重要的理论与实践意义。

2 亲属关系知识库

2.1 亲属关系的谓词表示

亲属关系的表达可以通过逻辑谓词来进行数学表达，即R(x,y)，其中的x 和y 为人物变量，表示亲属关系中的主语和宾语，即为x称呼y为R。例如，夫(韩梅，李雷)来表达韩梅和李雷的关系，表示韩梅称呼李雷为夫。

2.2 外围知识库

亲属关系的代数推理是建立在完备的亲属关系知识库的基础上。完整、丰富的亲属认知模型和准确的亲属关系模型，对于亲属关系推演起到至关重要的作用。亲属认知模型的多元的属性表达，在对于一些复杂亲属关系推演中歧义消解起到至关重要的作用。

区别于国外的uncle，国内对应称呼为叔叔，伯伯。所以在构造亲属模型时，同辈的年龄大小也被考虑在系统模型推演中，对应的知识库构建时年龄也被作为一项重要指标纳入到性质库的指标当中。

（1）亲属名词

亲属名词是亲属之间的称谓，表达一种亲属关系，一种亲属关系的亲属名称在不同的应用场景下有多种表达方式。例如，“父亲”“爸爸”“爹”“家父”都是表示同一种亲属关系的亲属名词，根据不同的场景才有不同的名词表述。我们在构建亲属名词针对同一种关系的亲属名词进行了分类。例如：R1父亲(x,y)=R2家父(x,y)。

（2）亲属关系

亲属关系是描述人物之间的社会联系。通过逻辑谓词进行表达R(x,y)。

2.3 性质库

性质库是亲属关系以及亲属关系中所包含的隐含关系的集合。性质库作为性质判断的重要依据，在代数推理上是重要的理论依据。例如，兄长(x,y)=>男(x)∧男(y)∧(y>x)。亲属关系、亲属的各种属性（性别、年龄）以及属性关系的集合统称为性质库。

2.4 逆判断库

在亲属关系中，主语和宾语的关系是相互的。同时在汉语逻辑中存在大量的逆关系。这种主宾互换，关系转换的运算叫逆判断。在谓词逻辑中可以通过求逆运算来实现。例如R父亲（x,y）<=>R孩子(y,x)。R孩子即为R父亲的逆判断。

汉语中存在大量的亲属关系和逆判断。例如父子<=>子父，夫妻<=>妻夫，兄弟<=>弟兄通过对每种亲属关系的逆判断进行整理，完成逆判断库的构建。

2.5 传递库

亲属关系推演过程中，需要通过间隔多人的层层关系的推理传递完成。例如，R弟(x,y)∧R妻(y,z)=>R弟媳(x,z)。存在中间人的亲属关系的推理，通过两层谓词逻辑和共有的中间人，完成亲属逻辑的传递。通过对基本的传递信息的构建，来完成亲属代数关系推演中的关系推理。

3 亲属关系的代数表示模型

3.1 采用代数表示模型的动机

代数表示模型的构建基于亲属关系的如下事实：

（1）每个亲属关系都有一个参考点，例如“小明的父亲”“我的爷爷”。

（2）复杂的关系可以表达成一系列有序的简单关系的组合。例如，“我的叔叔”是“我的爸爸的弟弟”，x表示我，y表示爸爸，z表示弟弟，R叔叔(x,y)=R爸爸(x,z)∧R弟弟(z,y)。

（3）亲属关系本身是一种从一个关系集合到另一个关系集合的映射。以自己为参考点，“父亲”这一关系将“我”映射到“我的父亲”这一个单元素集合；再对“我的父亲”这一个单元素集合进行“哥哥”这一关系的映射，则映射的结果为“我的伯伯”这样一个集合，它可能是空集、单元素集合或者多元素集合。

（4）每个亲属关系都可以定义一个逆关系，一个关系的逆关系可能唯一比如“丈夫”的逆关系是“妻子”；也可能不唯一，比如“父亲”的逆关系为“儿子or 女儿”，R父亲(x,y)<=>R孩子(y,x)∧(R男(x)∨R女(x))。

（5）复合的亲属关系满足结合律，例如：父亲的父亲的母亲=爷爷的母亲=父亲的奶奶，R父亲(x,y)∧R父亲(y,z)∧R母亲(z,w)=R爷爷(x,z)∧R母亲(z,w)=R父亲(x,y)∧R奶奶(y,w)。

综上，可以使用一个代数系统来描述亲属关系。为了建立这样一个代数系统，主要有两个子任务：确立要考虑的亲属关系的集合，定义集合内元素之间的运算表。

3.2 代数表示模型的建立

首先确定要研究的亲属关系，中国是一个幅员辽阔的多民族国家，不同的地域和民族对亲属中国亲属关系主要分为血亲和姻亲两大类[3]，血亲是指由生育关系确立的亲属关系，姻亲指的是由婚姻产生的亲属关系。此外中国的亲属关系还要考虑长幼、性别等因素，这也是中国的亲属关系体系与西方的一个显著的不同的地方，例如父亲的兄长叫伯父，父亲的弟弟叫叔父；又比如父亲的姐妹叫姑姑，而母亲的姐妹叫姨母。亲属关系的体系繁杂，并且其中的遵循原则并非在所有的关系上都普遍适用，例如伯父和叔父是由和父亲的长幼关系区分，但是姑母无论和父亲长幼关系如何都叫姑母。这使得亲属之间的运算关系很难用简单的一些规则定义出来，因此要定义亲属关系的运算规则，应该采用运算表的方式定义。

表示二元运算*的运算表是一个二维表格，二元运算*的运算表的行列标号均由集合R中的所有元素构成，在行列交汇的格子内，记录相对应行列的元素进行*运算后的结果。因此本文需定义的运算表是一个56*56的表格，只要将这一表格填满即完成亲属关系的代数表示模型的构建。inv运算的运算表是一个元素数目和R集合基数相等数目的字典，由R中元素作为键，inv运算的结果作为值。如表2和表3分别展示了部分inv运算表和亲属关系的二元运算*的运算表的称谓均有差异，但是其中依然有些原则是普适的。为了应用于实际，必须将全国各地的亲属关系称谓标准化。本文将在国标GBT-4761-2008[5]家庭关系代码中包含的亲属关系的基础上进行后续的工作，此举能够保证模型可以方便地运用于大多数场景。

表1 纳入考虑的亲属关系集合

表2 求逆运算inv运算表（部分）

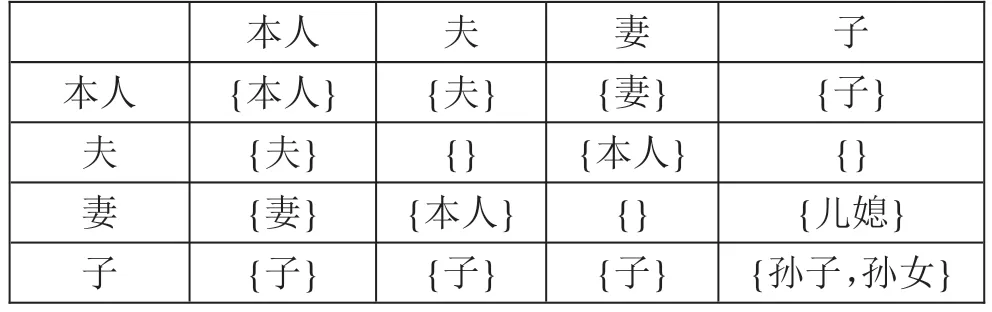
表3 亲属关系乘法运算表（部分）

GBT-4761-2008 中有两种亲属关系代码，用一位数字表示的亲属关系代码和用两位数字表示的亲属关系代码，由于一位数字代码表达的亲属关系较为粗略，因此本文采用两位数字代码表示的亲属关系作为研究集合。不过这一关系集合中包含一些不利于处理的关系，需要进行删减。如其中包含的“配偶”“妻”“夫”这三个关系，互相有包含关系，删去“配偶”这一关系不会影响最终模型的表达能力，还可以减少冗余信息。经过调整之后最终确立如表1 所示共计56 种关系组成的关系集合。

确立了以上的关系集合，记为R，∀A∈R，可以定义求逆运算inv，inv(A)的运算结果是R的一个子集，这一运算可以通过一个行数与R 中元素个数相同运算表来定义。接下来要在R 上定义亲属关系的二元运算*（读作亲属关系乘法），这个运算有如下性质：

（1）“本人”是R中的单位元，对任意A∈R，有本人*A=A*本人=A；

（2）∀A∈R,inv(A)=φ，满足 本人∈φ；

护理工作辛苦繁琐、排班制度不稳定调动大，护理人员社会地位低、不受尊重是在广大护生中的普遍印象。许多人对护理工作存在偏见,把为病人提供日常生活照顾、打针、发药作为护理工作的全部。护理本科在校生主要是在校内课堂上学习专业基础知识以及在实验室学习操作技术，并没有在临床上与病人进行面对面的交流沟通，因此，对于即将从事的职业或多或少会缺乏信心，甚至出现焦虑、恐惧等心理。

（3）*运算满足结合律；

（4）任意A,B∈R,代数式A*B的运算结果是一个集合φ,(φ∈R)；

（5）由于*的运算结果是一个集合，对于一个集合φ,(φ∈R)和∀A∈R之间，同样需要定义运算，定义如下：

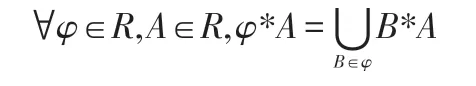
（6）对于两个集合φ1,φ2(φ1,φ2⊆R)，定义两者之间的*运算：

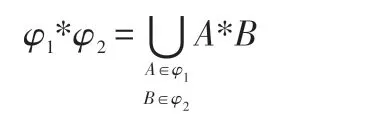
4 基于代数表示模型的亲属关系推理

在亲属关系的代数表示模型建立完成之后，即可应用这一表示模型进行亲属关系的推理。本文所述的推理，主要解决如下问题：给定一个由n个人组成的集合，已知其中部分成员之间的亲属关系（用前述R集合中的关系表述），要通过推理回答集合中任意两个成员之间有何种亲属关系。

首先，集合成员之间的关系用图来表示是非常自然的，由于亲属关系是有方向的，因此应该用有向图来表述亲属关系，每个人用一个顶点表示，两个人之间有某种亲属关系，则在两人之间连上箭头并在箭头上标注关系种类，下称此图为亲属关系图。根据代数表示模型，每个关系都能求逆，当已知a到b有亲属关系A时，可以得出b到a有亲属关系inv(A)，因此，实际上亲属关系图中任意两个顶点之间的箭头都是成对出现的。中国的亲属关系系统中，性别是一个重要的考虑因素，在将已知信息表示成亲属关系图的过程中，如果亲属关系能够断定人物的性别，应当对人物性别做标记，便于推理时获得更加精确的备选关系集合。

要通过已知的亲属关系找到未知的两个人之间的亲属关系，可以理解成在亲属关系图中找到两人之间的一条路径，然后将路径上的每一条边上的关系用*运算连接起来，结果就是两人之间的关系。当然如果不存在这样一条路径，那就说明当前信息不足以推断出两人之间的亲属关系；如果存在多条路径，那么每一条都能够表示两人之间的亲属关系，但是两条不同路径获得的信息量不一样，得出的备选的关系集合会有不同，但均包含真正的关系。

在获得了两人之间的路径后，沿着路径依次取出每条边上的关系集合，用“*”连接在一起构成一个代数式子，这一代数式就是两者之间的亲属关系表达式，但是这一表达式往往不符合习惯表达，还要根据运算表进行化简。

根据以上论述，提出如下亲属关系推理算法：

算法1 亲属关系推理算法

（1）begin

（2）预先定义求逆运算表INV，亲属关系乘法(*)运算表MUL

（3）Graph G; //亲属关系图

（4）Dict Gender; //标记性别的字典

（5）for relation in relationInputs:

（6）对每个输入的关系，在图中添加相应边，边的附属数据域存储关系名称的集合;

（7）如果关系包含性别信息，在Gender字典中记录;

（8）end for

（9）for relation in relationInputs:

对每个输入的关系，在图中添加与之相应的逆关系的边；

根据Gender 中的性别信息删除边的附属数据域中不符合性别限定的关系;

（10）end for

（11）//完成亲属关系图的构造

（12）Input:想要查询关系的两人A、B

（13）Path=图G中A、B两人之间的一条路径;

（14）AlgebricExp=Path对应的代数式;

（15）result=AlgebricExp[1];

（16）for i=2 to length(AlgebricExp):

（17）result=relationMultiply(result,AlgebricExp[i]);

（18）//relationMultiply是亲属关系乘法运算的实现

（19）在result中删除不符合性别限定关系的元素;

（20）end for

（21）output result

（22）end

5 基于代数表示模型的亲属关系推理示例

已知：B是A的儿子，C是B的女儿，E是A的女儿，G是E的儿子，G是C的表兄弟，E是F的妻子。求问：F是C的何种亲属？

解决步骤如下：

（1）建立一个图，把已知关系作为附带关系的边填到图中，得到如图1所示亲属关系图，同时在此过程中将会确定性别信息：B、G、F为男性，C、E为女性。

图1 已知亲属关系图

（2）补全亲属关系图中的逆关系对应的边：以B、C 为例，C是B的女儿，查询inv运算表可知女儿的逆关系为“{父亲，母亲}”，已知B 是男性，排除“母亲”，因此C 指向B 的箭头应该标注父亲。以此类推可以得到如图2的亲属关系图。

图2 补全逆关系后的亲属关系图

（3）寻找C到F的路径确定C和F的亲属关系：C到F有两条路径，CGEF和CBAEF。

（4）先看CGEF 这一条路径，转化成亲属关系代数式为“表兄弟*母亲*夫”，通过计算表进行如下化简计算：

表兄弟*母亲*夫={姑母，舅母，姨母}*夫={姑父，姨父，舅父}

因此可以得出F是C的姑父、姨父或者舅父。

（5）再看CBAEF这一条路径，转化成亲属关系代数式为“父亲*{父亲，母亲}*女*夫”，通过计算表进行如下化简计算：

父亲*{父亲，母亲}*女*夫={爷爷，奶奶}*女*夫=姑母*夫=姑父

因此可以得出F是C的姑父。

可以看到这两种路径得到了不一样的运算结果，F 实际上是C的姑父，两个计算路径得出的结果集合都包含正确的答案。事实上这两者均是正确的，只是它们推理时考虑到的信息不一样，得出了精确度不同的结果。现实生活中，倘若C 告诉他人“E 是我表兄弟的母亲，F 是E 的丈夫”，依据这句话根本不足以判断F是C的姑父，因为决定F是C的姑父、姨父还是舅父的关键信息是E 和C 的父亲具有相同的父亲或者母亲，而CGEF这条关系路径则忽略了这一关键信息。要找出最精确的答案，目前本文还没能给出有效方案，但是在图中节点较少且边比较稀疏的时候，可以使用一个暴力搜索的方法：求出所有的路径，选择结果集元素个数最少的一个。在节点数多、边稠密的情况下，暴力搜索的理论最差算法复杂度为O(n!)，此外还可以采取求出一条最短路径的方案，这样虽然可能降低结果的精准程度，但是规避了算法复杂度的影响。

6 结语

本文通过总结人们日常表述亲属关系的方式的特征，将亲属关系本身看成是一种把一个亲属关系集合映射到另一个亲属关系集合的映射规则，进而发现这些规则之间的复合满足一些代数运算的性质，因而建立了基于代数系统的亲属关系表示系统。在国标GBT-4761-2008 所包含的亲属关系的基础上确立了要研究的亲属关系的集合，然后通过计算表在此集合上定义了求逆运算和亲属关系的二元运算（*），最后提出了通过亲属关系图表示已知亲属关系知识的方法，并且在此基础上提出了用亲属关系图中两个节点的路径来表示两节点的亲属关系的推理算法，通过伪代码和例子的方式阐明了算法的运行过程，证明了算法的可行性。

本文提出的方法基于对人类思考亲属关系问题的过程的模仿，同时借助了代数学的理论，为研究亲属关系的表示和推理问题提供了一个新的视角，但是本方法也有结果精确度受中间运算过程的影响等问题，这些问题还需要进一步研究。