坡代数的反犹豫模糊子坡代数
姜 曼
(西安交通工程学院 公共课部,陕西 西安 710300)
0 引言
1965年,Zadeh[1]提出了模糊集,这是一种描述模糊现象的方法.模糊集的提出,对研究代数结构起着非常重要的作用.在此基础上,相继出现了直觉模糊集[2],区间值模糊集[3],双极值模糊集[4]等理论,这些理论作为研究代数结构的重要工具,使得代数结构理论更清晰化.特别的,Torra[5]提出了犹豫模糊集概念,犹豫模糊数在考虑问题全面性上比传统模糊元更具有优势,在各个数学模型中都能得到广泛应用[6-7].
1981年,我国控制论专家曹志强[8]提出了坡代数,并且在专著中详细介绍了坡代数的理论[9].用模糊集的理论研究坡代数,现在已经出现了很多结论,比如:Jun等[10]研究了坡代数的模糊子坡(理想);赵虎等[11]把坡代数与模糊软集相结合,研究模糊软坡代数;王丰效[12-13]把坡代数与区间值模糊集相结合,研究坡代数区间值模糊子坡代数、坡代数的区间值模糊理想,有关坡代数的其它结论,可见文献[14-16].关于坡代数和模糊集相结合的研究,现阶段已经有了很多成果,但是用模糊集的拓展——犹豫模糊集来研究坡代数,这在之前的研究中还没有相关成果.因此,在现有的模糊集理论研究基础上,为了填补坡代数上犹豫模糊子代数研究的理论空白,本文提出了坡代数上的反犹豫模糊子坡代数,研究反犹豫模糊子坡代数的基本性质、反直积以及同态像等,得出的相关结论进一步丰富了对坡代数和犹豫模糊集的研究.
1 预备知识
定义1[8]设X是一个非空集合,在X中定义两个二元运算加法(记为“+”)和乘法(记为“*”),若∀x,y,z∈X,都有
(1)x+y=y+x;
(2)(x+y)+z=x+(y+z);
(3)(x*y)*z=x*(y*z);
(4)x*(y+z)=x*y+x*z;
(5)(y+z)*x=y*x+z*x;
(6)x+x=x;
(7)x+x*y=x;
(8)y+x*y=y;
则称(X,+,*)为坡代数.
若(X,+,*)是一个坡代数,在X中定义关系≤如下:对任意x,y∈X,x≤y当且仅当x+y=x,则≤是X上的一个偏序关系.
定义2[9]设(X,+,*)是一个坡代数,S是X的非空子集,若S关于X的两种运算封闭,则称S是X的子坡.
定义3[5]设(X,+,*)是一个坡代数,A是X上的模糊集,若对任意x,y∈X,都有A(x+y)∧A(x*y)≥A(x)∧A(y),则称A是(X,+,*)的模糊子坡代数.
定义4[5]设U是一个非空集合,一个U上的犹豫模糊集F的定义如下:
F:{(x,hF(x))|x∈U},
其中,hF(x)是由区间[0,1]上若干个不同值构成的集合,表示U中的元素x属于集合F的若干种可能隶属度.记U上的犹豫模糊集的全体为HF[U].
设F为U中的犹豫模糊集,P([0,1])为区间[0,1]的幂集.称集合
U(F,γ):={x∈U|γ⊆hF(x)},
为F的犹豫水平集,其中γ⊆P([0,1]).
定义5[5]设U是一个非空集合,F和G是U上的犹豫模糊集,且具有如下形式:
F:{(x,hF(x))|x∈U},
G:{(x,hG(x))|x∈U}.
规定如下运算:
(1)补:对于F,它的补元Fc定义为:
补运算满足对合律,即(Fc)c=F.
(2)并:F和G的并F∪G定义为:
hF∪G(x)=hF(x)∪hG(x)=
{h∈hF(x)∪hG(x)|h≥max(hF(x),hG(x))},
(3)交:F和G的交F∩G定义为:
hF∩G(x)=hF(x)∩hG(x)=
{h∈hF(x)∩hG(x)|h≤min(hF(x),hG(x))}
.
2 反犹豫模糊子坡代数
本文若无特殊说明,均用X表示坡代数.
定义6设X是一个坡代数,A∈HF[X],若对于∀x,y∈X,都有
hA(x+y)∩hA(x*y)⊇hA(x)∩hA(y),
则称A是X的犹豫模糊子坡代数.
记X上的全体犹豫模糊子坡代数为HFSL[X].
定义7设X是一个坡代数,A∈HF[X],若对于∀x,y∈X,都有
hA(x+y)∪hA(x*y)⊆hA(x)∪hA(y),
则称A是X的反犹豫模糊子坡代数.
记X上的全体反犹豫模糊子坡代数为AHFSL[X].

定理1设A∈HF[X],则A∈AHFSL[X]当且仅当∀ε∈[0,1],X(A,ε)≠∅是X的子坡代数.
证明如果A∈AHFSL[X],则对∀x,y∈X,由hA(x+y)∪hA(x*y)⊆hA(x)∪hA(y),因为X(A,ε)≠∅,则对∀x,y∈X(A,ε),有hA(x)⊆ε,hA(y)⊆ε.因此hA(x+y)∪hA(x*y)⊆hA(x)∪hA(y)⊆ε∪ε=ε,因此hA(x+y)⊆ε,hA(x*y)⊆ε,从而可得x+y∈X(A,ε),x*y∈X(A,ε),故X(A,ε)是X的子坡代数.
反之,假定∃a,b∈X,使得hA(a+b)∪hA(a*b)⊃hA(a)∪hA(b).令s∈[0,1],且满足hA(a+b)∪hA(a*b)⊃s⊃hA(a)∪hA(b),即hA(a)⊂s,hA(b)⊂s,因此a,b∈X(A,s).因为X(A,s)是X的子坡代数,所以a+b∈X(A,s),a*b∈X(A,s),因此hA(a+b)⊂s,hA(a*b)⊂s,故hA(a+b)∪hA(a*b)⊂s,这与hA(a+b)∪hA(a*b)⊃s矛盾.因此,对任意x,y∈X,有hA(x+y)∪hA(x*y)⊆hA(x)∪hA(y).所以A∈AHFSL[X].
定理2设A∈HF[X],则A∈AHFSL[X]当且仅当

是X的子坡代数.
证明同定理1.

证明必要性.如果A∈AHFSL[X],则对∀x,y∈X,即有hA(x+y)∪hA(x*y)⊆hA(x)∪hA(y).因此

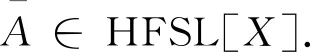
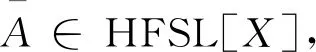
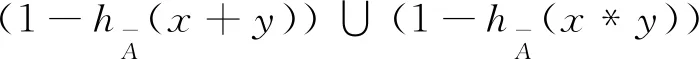
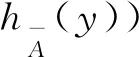
定义9设A、B∈HF[X],∀x∈X,定义A与B的并为(A∪B)(x)=A(x)∪B(x),其中hA∪B(x)=hA(x)∪hB(x).
定理4设A,B∈AHFSL[X],∀x∈X,则A∪B∈AHFSL[X].
证明因为A,B∈AHFSL[X],所以∀x,y∈X,都有
hA(x+y)∪hA(x*y)⊆hA(x)∪hA(y),
hB(x+y)∪hB(x*y)⊆hB(x)∪hB(y).
hA∪B(x+y)∪hA∪B(x*y)=
(hA(x+y)∪hB(x+
y))∪(hA(x*y)∪hB(x*y))=
(hA(x+y)∪hA(x*y))∪(hB(x+
y)∪hB(x*y))⊆
(hA(x)∪hA(y))∪(hB(x)∪hB(y))=
(hA(x)∪hB(x))∪(hA(y)∪hB(y))=
hA∪B(x)∪hA∪B(y)
因此,A∪B∈AHFSL[X].
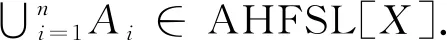
证明同定理4.
3 坡代数的反犹豫模糊子坡代数的反直积
定义10若S1,S2为非空集合,且A∈HF[S1]和B∈HF[S2].则对∀(x,y)∈S1×S2,定义如下映射A⊗B:S1×S2→P([0,1]):A⊗B(x,y)=A(x)∪B(y).其中hA⊗B(x,y)=hA(x)∪hB(y),则称A⊗B是S1×S2的犹豫模糊子集,并称A⊗B为犹豫模糊集A与B的反直积.
引理1[9]设(X,+,*)和(Y,+,*)是两个坡代数.在X×Y上定义两种加法+和乘法*运算如下:对∀(x1,y1),(x2,y2)∈X×Y,规定(x1,y1)+(x2,y2)=(x1+x2,y1+y2),(x1,y1)*(x2,y2)=(x1*x2,y1*y2).则X×Y关于上述运算构成一个坡代数.
定理5若A∈AHFSL[X],B∈AHFSL[Y],则A⊗B∈AHFSL[X×Y].
证明∀(x1,y1),(x2,y2)∈X×Y,因为A∈AHFSL[X],B∈AHFSL[Y],所以有
hA(x1+x2)∪hA(x2*x2)⊆
hA(x1)∪hA(x2),hB(y1+y2)∪hB(y1*y2)⊆
hB(y1)∪hB(y2).
因此可得
hA⊗B((x1,y1)+(x2,y2))=
hA⊗B(x1+x2,y1+y2)=hA(x1+
x2)∪hB(y1+y2).
hA⊗B((x1,y1)*(x2,y2))=
hA⊗B(x1*x2,y1*y2)=
hA(x1*x2)∪hB(y1*y2).
hA⊗B((x1,y1)+
(x2,y2))∪hA⊗B((x1,y1)*(x2,y2))=
(hA(x1+x2)∪hB(y1+
y2))∪(hA(x1*x2)∪hB(y1*y2))=
(hA(x1+x2)∪hA(x1*x2))∪(hB(y1+
y2)∪hB(y1*y2))⊆
(hA(x1)∪hA(x2))∪(hB(y1)∪hB(y2))=
(hA(x1)∪hB(y1))∪(hA(x2)∪hB(y2))=
hA⊗B(x1,y1)∪hA⊗B(x2,y2)
综上,A⊗B∈AHFSL[X×Y].
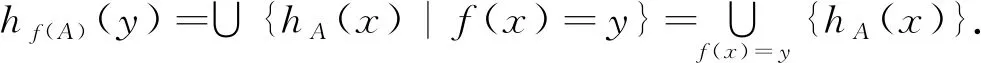
证明因为f:X→Y为同态满射,则对∀y1,y2∈Y,∃x1,x2∈X,有f(x1)=y1,f(x2)=y2.因此可得:
hf(A)(y1+y2)=∪{hA(x)|f(x)=
y1+y2}=∪{hA(x1+x2)|f(x1+x2)=
y1+y2}=∪{hA(x1+x2)|f(x1)+f(x2)=
hf(A)(y1*y2)=∪{hA(x)|f(x)=y1*y2}=
∪{hA(x1*x2)|f(x1*x2)=y1*y2}=
∪{hA(x1*x2)|f(x1)*f(x2)=
因为A∈AHFSL[X],所以对∀x1,x2∈X,都有

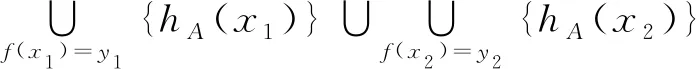
综上,f(A)∈AHFSL[Y].
定理7设X和Y是两个坡代数.f:X→Y为同态满射.若B∈AHFSL[Y],则f-1(B)∈AHFSL[X].其中hf-1(B)(x)=hB(f(x)).
证明∀x1,x2∈X,因为f:X→Y为同态满射,所以∃y1,y2∈Y,有f(x1)=y1,f(x2)=y2.因为B∈AHFSL[Y],所以hB(y1+y2)∪hB(y1*y2)⊆hB(y1)∪hB(y2).因此
hf-1(B)(x1+x2)∪hf-1(B)(x1*x2)=
hB(f(x1+x2))∪hB(f(x1*x2))=
hB(f(x1)+f(x2))∪hB(f(x1)*f(x2))=
hB(y1+y2)∪hB(y1*y2)⊆hB(y1)∪hB(y2)=
hB(f(x1))∪hB(f(x2))=
hf-1(B)(x1)∪hf-1(B)(x2).
综上,f-1(B)∈AHFSL[X].

