单颗磨粒刻划氧化镓晶体表面的裂纹成核位置及扩展方向研究

周 海 张杰群 徐亚萌 沈军州 黄梦蝶

盐城工学院机械工程学院，盐城，224051

0 引言

单晶氧化镓(β-Ga2O3)是近年来备受关注的第四代半导体材料，其带隙为4.9eV，大于GaN的3.4eV和SiC的3.3eV，相比于其他半导体材料，具有击穿电场强度高、热导率小、抗辐射能力强和化学稳定性良好等特点，在功率半导体和LED照明中具有广泛的应用前景[1-3]。氧化镓为硬脆性的单晶材料，易于裂解，难以加工，在超精密加工过程中遇到应力集中时会发生微裂纹断裂，当局部集中应力过大时，可能会发生大规模的劈裂和剥落[4]。裂纹的存在和扩展很大程度限制了氧化镓晶体的工程应用，因此，深入探索氧化镓晶体刻划过程中磨粒下方的应力分布，有助于了解裂纹形成和扩展的机理，对晶体后续加工工序的顺利进行具有重要意义。

目前，关于单颗磨粒刻划脆性材料的裂纹成核位置及扩展情况已有许多研究成果。WANG等[5]分别对石英玻璃与BK7硅酸盐玻璃进行单颗磨粒刻划试验，对比得出石英玻璃的裂纹形成机理；李新颖[6]针对多晶硅材料进行了单颗磨粒的刻划试验，并与QIU等[7]对玻璃陶瓷的刻划试验数据进行比对，分析得出多晶硅材料的裂纹成核位置及扩展方向。然而，关于氧化镓晶体的裂纹成核扩展，国内外学者目前还没有进行深入的研究。裂纹的成核位置及扩展方向影响材料的超精密加工，因此，了解氧化镓晶体的应力分布及裂纹成核扩展情况非常重要。

1 单颗磨粒刻划过程中弹性应力场的解析模型

如图1所示，当磨粒刻划硬脆材料表面时，施加的刻划力可以进一步分解为施加到工件表面的法向力分量Fn和沿刻划方向的切向力分量Ft。假设切向力分量与法向力分量的比值为λ，即Ft=λFn，λ的取值可由磨粒的半锥角ψ确定[8]：

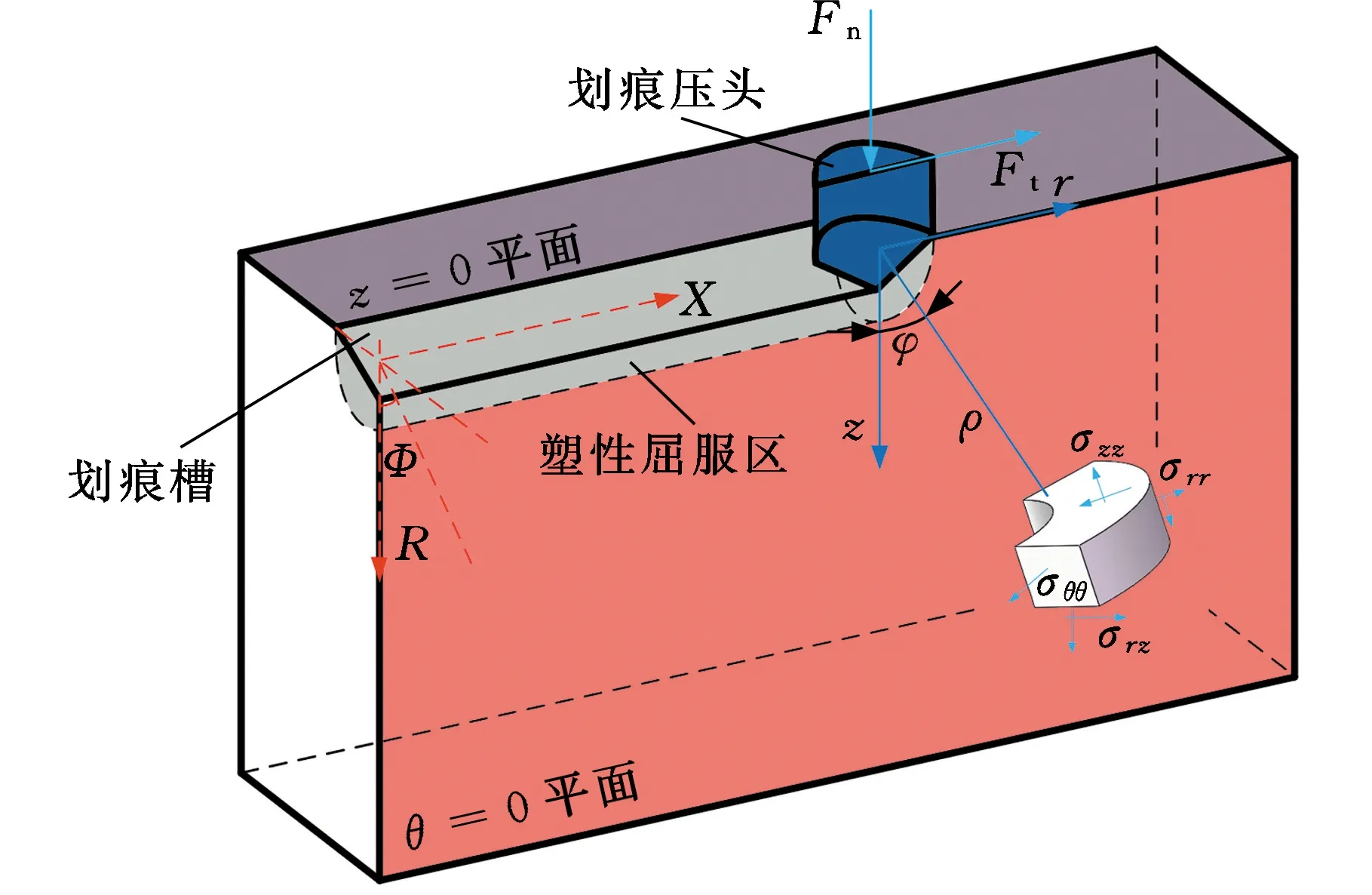
图1 单颗磨粒刻划的坐标系

(1)

假设β-Ga2O3(010)面为一个无限大半空间的弹性介质，磨粒为刚性压头，根据弹性理论，在研磨过程中，磨粒与晶面的接触可以表示为半空间体在边界上承受集中载荷的空间问题。法向载荷作用于晶面接触区域的弹性应力场分布使用Boussinesq解计算，而切向集中力则使用Cerruti解计算。此外，压头的顶尖压入晶面后，会在接触点处产生一个应力奇异点，导致材料倾向于发生塑性变形来抵消奇异效应。塑性变形的出现使得Boussinesq解和Cerruti解不能完整地描述压头和晶面接触区附近的弹性应力场。假设上述应力奇异点引起压头顶尖下方发生塑性变形，产生刚性的半球形“塑性核”，外载荷作用在“塑性核”上，使“塑性核”对晶面产生弹性应力场，则该弹性应力场需要通过Blister应力场的Yoffe解来进行计算[9]。

根据弹性理论，利用叠加原理获得压头压入晶面后的弹性应力场[5，10]，计算公式为

σij=αij+βij+γij

(2)

式中，αij为Boussinesq应力场解对应的应力张量分量；βij为Cerruti应力场解对应的应力张量分量；γij为Blister应力场解对应的应力张量分量。

1.1 法向载荷与切向载荷引起的弹性应力场

刻划过程中，法向力Fn在材料内部引起的弹性应力场可视为受法向集中载荷作用所形成的Boussinesq问题，图1中柱坐标系(r,z,θ)所对应的解为[11]

(3)

式(3)中，柱坐标原点为磨粒顶部作用点，ρ为接触应力场中任一点到柱坐标原点之间的距离，ν为泊松比，其中，氧化镓晶体泊松比是0.27，φ为ρ和z轴的夹角，如图2所示。此外，当θ=0时，r=ρsinφ，z=ρcosφ。

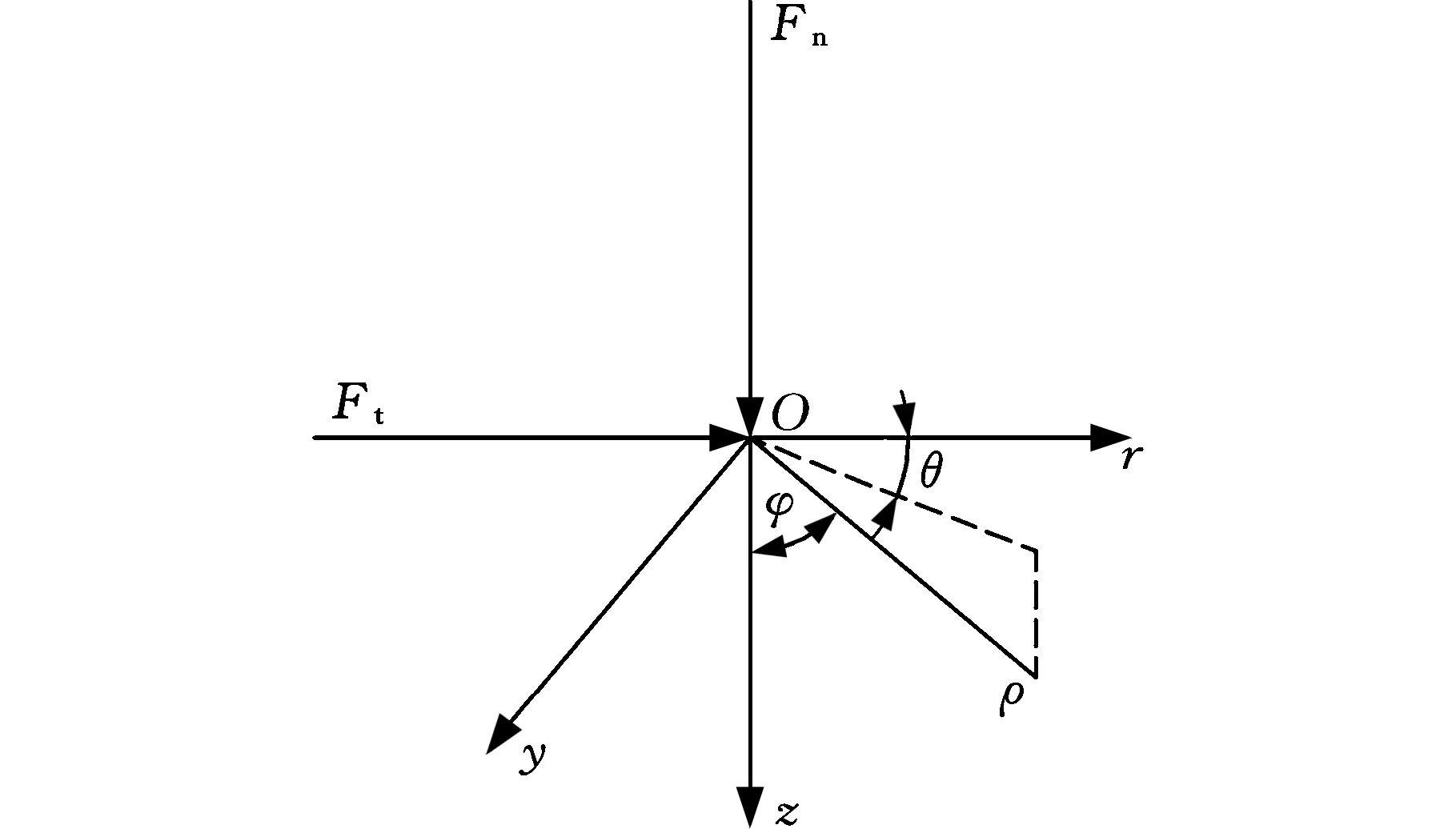
图2 压头接触的圆柱坐标系

式(3)可以写成如下通式：

(4)

与之相似，切向载荷分量Ft在材料内部形成的弹性应力场分布一般情况下视为Cerruti问题，在图1中柱坐标系(r,z,θ)条件下的解为[11]

(5)

可以写成如下通式：

(6)

1.2 材料塑性变形引起的Blister残余应力场

在单颗磨粒刻划氧化镓晶体(010)晶面过程中，除了刻划力Fn和Ft会对其应力分布产生影响外，塑性屈服区作为应变源，也会对弹性应力场造成一定的影响(即Blister残余应力场)。基于传统的压痕断裂力学理论，径向裂纹在材料的自由表面，划痕的两侧塑性域边缘处成核[12]。因此，为了方便观察径向裂纹，重点研究氧化镓晶体(010)晶面内影响径向裂纹成核的应力场。

在氧化镓晶体(010)晶面内(即z=0时)，应力场关于θ=0对称，因此，仅考虑0°≤θ≤180°的情况，当0°≤θ≤90°时，应力场处于磨粒的前方，Blister应力场可表示为[9]

(7)

式中，γij为Blister应力场解的应力偏张量分量；E为弹性模量；f为在残余应力作用下材料减少的体积系数；a为压头压入过程中的接触半径。

当90°<θ≤180°时，应力场处于磨粒后方的塑性变形区内，Blister应力场可表示为[9]

(8)

写成如下通式：

(9)

1.3 叠加后的弹性应力场

在单颗磨粒刻划作用下，弹性应力场分布是以上三个应力场的叠加。叠加后的通式写成：

(10)

当单颗磨粒刻划氧化镓晶体的深度为d时，引起的接触半径a=dtanψ。由硬度的定义H=Fn/(πa2)和式(10)得

(11)

根据HUANG等[13]对氧化镓晶体的研究可知，式(11)中，氧化镓晶体的fE/H为1.09，并且可以看出，材料内部任一点的应力与硬度的比值(σij/H)与磨粒载荷无关，只与磨粒的半锥角ψ及材料的性质有关。利用σij/H的值可以进一步分析径向裂纹的成核位置和空间几何分布的特征。

2 径向裂纹成核位置及扩展方向

径向裂纹成核的位置在磨粒刻划的工件表面，即氧化镓晶体(010)晶面，由式(3)、式(5)、式(7)、式(8)、式(11)可知，被刻划平面最大应力为

(12)

最大主应力的偏转角度可通过下式进行判断[6]：

(13)

2.1 压头刻划深度小于脆性转变临界切削深度

脆性转变临界切削深度(简称“临界切深”)是判定材料在去除加工中是处于塑性去除还是脆性去除的依据，当磨粒刻划深度小于临界切深时，材料以塑性剪切的方式被去除，材料表面未出现明显的脆性断裂，因此，这种情况下一般也不会出现中位裂纹与横向裂纹[6]。临界切深满足下式：

(14)

式中，dc为临界切深，根据文献[14]对氧化镓(010)面脆塑转变临界切深的分析可知dc=421.6 nm；Φ为量纲一的修正系数；KIC为断裂韧度，其中氧化镓(010)面的断裂韧度为0.782 MPa·m1/2。

用Cube金刚石压头模拟单颗磨粒进行刻划试验，通过MATLAB计算式(12)、式(13)，绘出氧化镓晶体刻划过程中在(010)晶面内的σmax/H应力分布图及σmax/H、σrz/H和偏转角α沿r/a轴正方向变化趋势图，见图3、图4。从图4中可以看出，最大正应力在r=-0.02a处取得最大值，σmax/H的最大值为1.320 56，径向裂纹最有可能在此处成核，偏转角为33.367 86°。

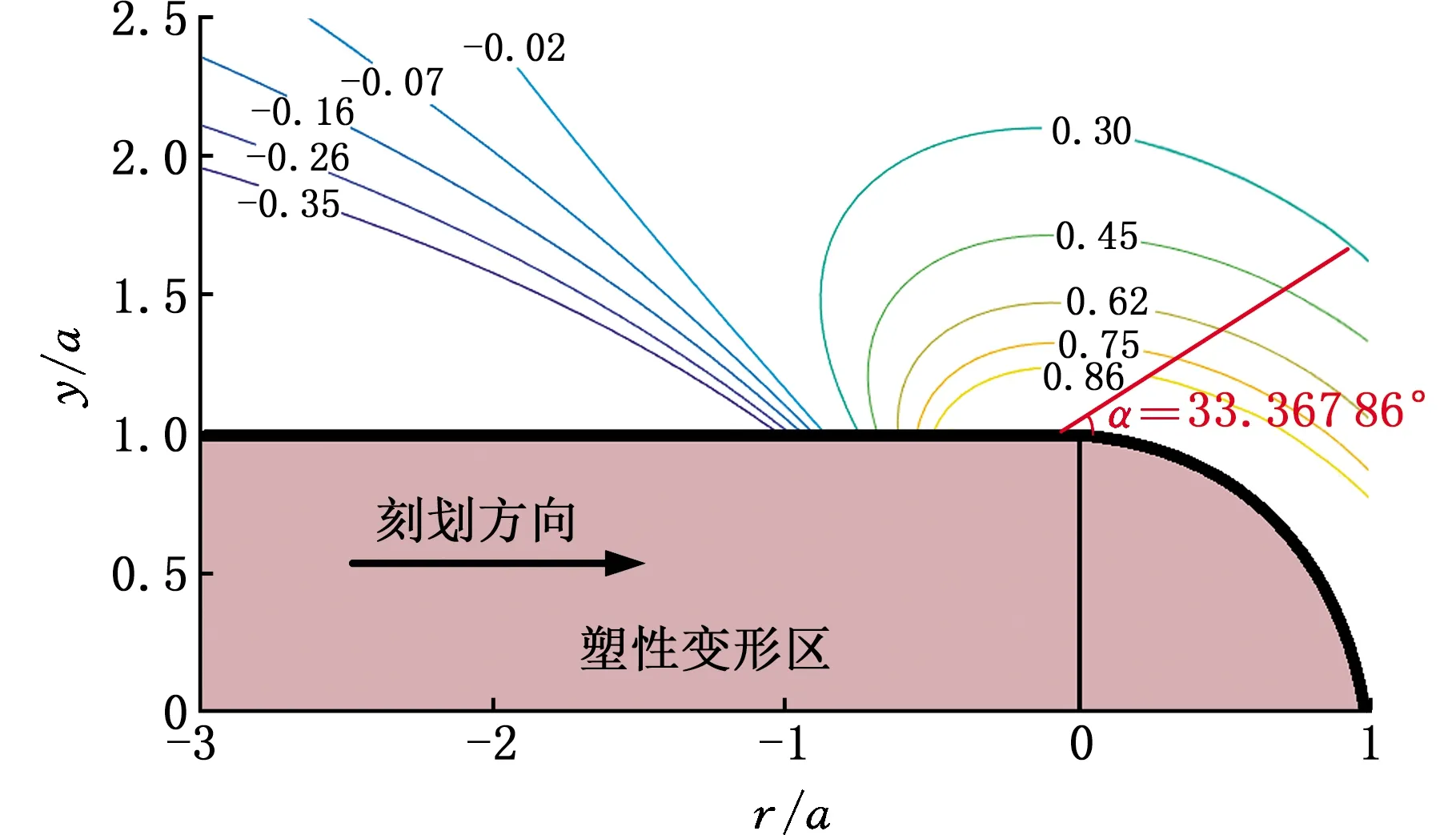
图3 氧化镓晶体刻划过程中在(010)晶面内的σmax/H应力分布图(无脆性断裂阶段)

图4 σmax/H、σrz/H和偏转角α沿r/a轴正方向变化趋势图(无脆性断裂阶段)

2.2 压头刻划深度大于脆性转变临界切削深度

当压头刻划深度大于脆性转变临界切削深度时，将以脆性破碎的方式去除材料，中位裂纹将在磨粒尖端下方塑性变形区边界处萌生，而中位裂纹的萌生和扩展将会削弱或消除由塑性变形引起的Blister应力场，最终可能导致径向裂纹只受法向载荷和切向载荷所产生的应力场的影响[6]。当应力场完全由法向载荷和切向载荷影响时，弹性应力场的表达式为

(15)

通过MATLAB计算式(12)、式(13)，绘出氧化镓晶体刻划过程中在(010)晶面内的σmax/H应力分布图及σmax/H、σrz/H和偏转角α沿r/a轴正方向变化趋势图,见图5、图6。从图6中可以看出，最大正应力在r=-0.55a处取得最大值，σmax/H最大值为1.219 25，径向裂纹最有可能在此处成核，此时，σrz/H为负值，所以，最大主应力偏转角应沿逆时针旋转90°，偏转角为51.448 62°。

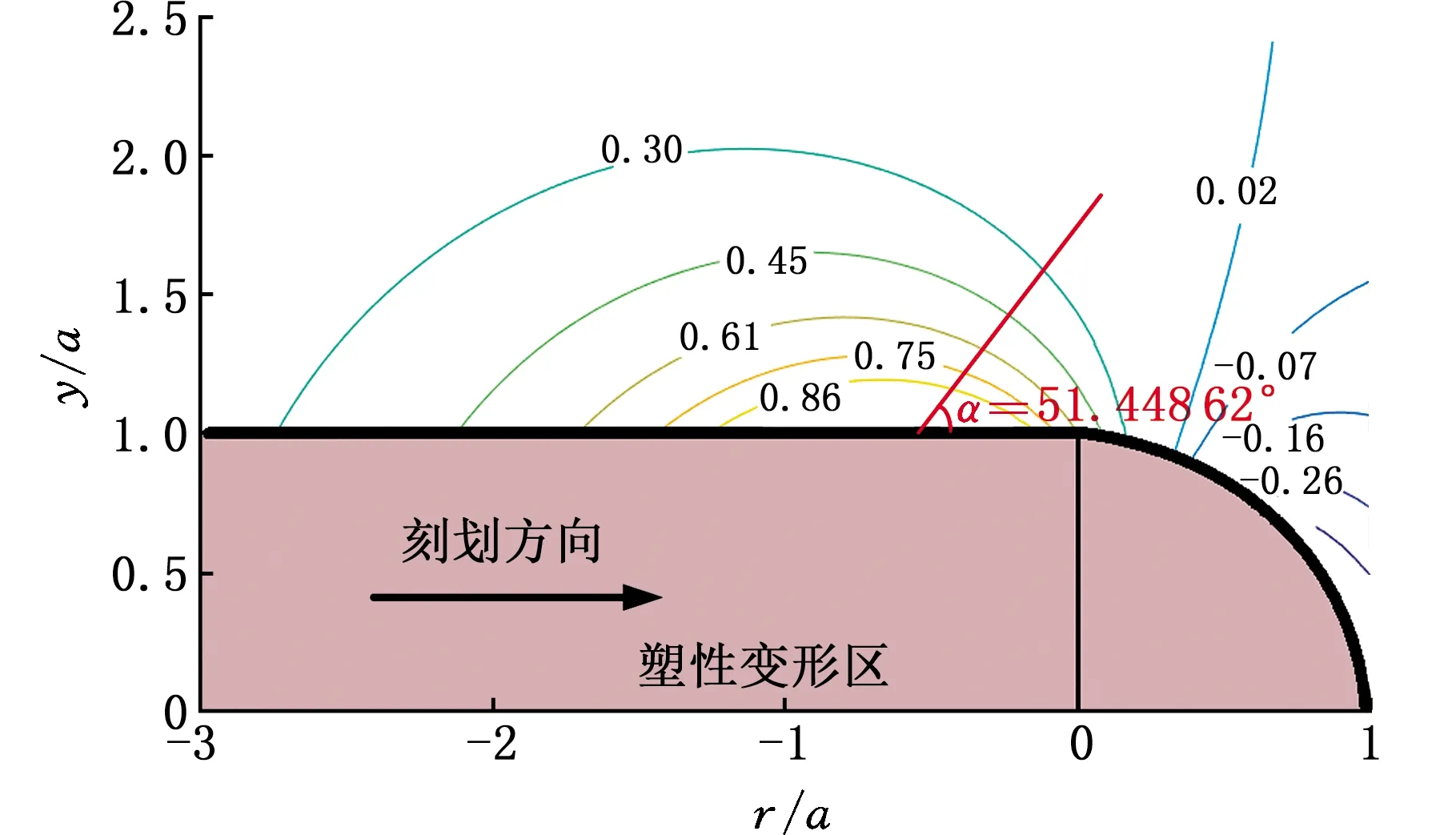
图5 氧化镓晶体刻划过程中在(010)晶面内的σmax/H应力分布图(脆性断裂阶段)

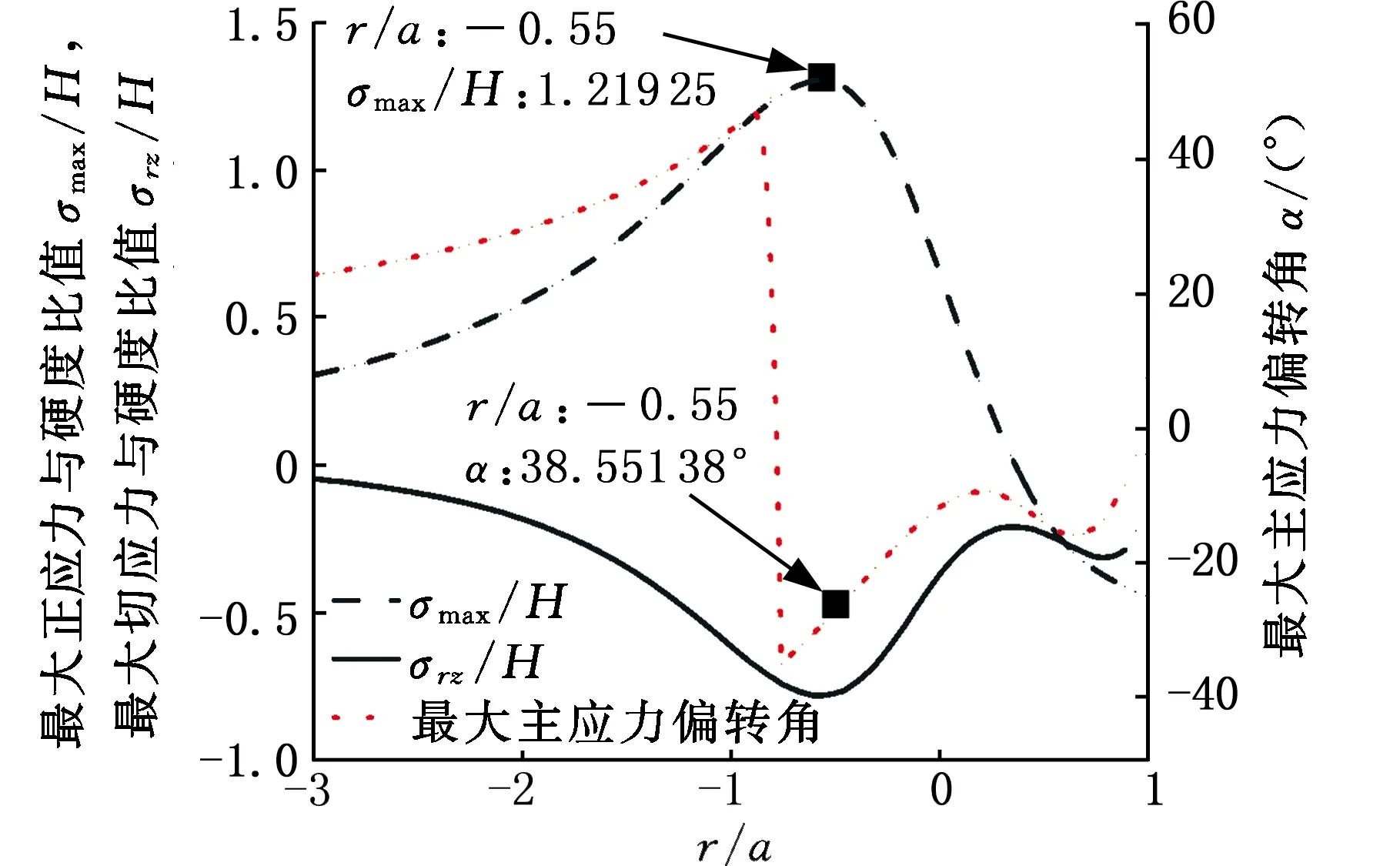
图6 σmax/H、σrz/H和偏转角α沿r/a轴正方向变化趋势图(脆性断裂阶段)

综上所述，当磨粒刻划氧化镓(010)面未发生脆性断裂时，径向裂纹的裂纹扩展方向与磨粒刻划方向之间的夹角为33.367 86°；当磨粒刻划氧化镓(010)面发生完全的脆性断裂时，径向裂纹的裂纹扩展方向与磨粒刻划方向之间的夹角为51.448 62°。因此，在磨粒刻划脆性材料过程中，随着载荷逐渐增大，径向裂纹的起始偏转角在33.367 86°～51.448 62°之间变化。

3 刻划试验

为了验证氧化镓晶体在单颗磨粒刻划作用下的弹性应力场模型，检验径向裂纹的成核位置和扩展方向的理论分析结果，采用Cube金刚石压头，以线性加载的方式刻划氧化镓晶体，并观察不同压入深度时的裂纹扩展方向。

3.1 试验样品以及压痕仪参数

试验样品采用中国电子科技集团公司第四十六研究所通过导模法制备的单晶氧化镓(β-Ga2O3)晶体，其主要晶面为(010)面，样品的尺寸(长×宽×高)为10 mm×10 mm×1 mm，样品经过研磨、化学机械抛光处理，加工后得到的晶体表面经过激光显微镜检测，其粗糙度值为4.8 nm。

纳米压痕试验设备采用美国安捷伦科技有限公司的G200型纳米压痕仪，此设备操作过程仅需输入相应参数就可以自动进行压痕划痕试验，保障了试验结果的稳定性和可重复性。该设备参数见表1，系统带有10倍和40倍物镜的光学显微镜，总放大倍率为250倍和1000倍。该设备在试验过程中会自动扣除所有热漂移效应，比一般的设备所测得的结果更加可靠。试验采用的压头为Cube金刚石压头，压头的几何参数见表2。

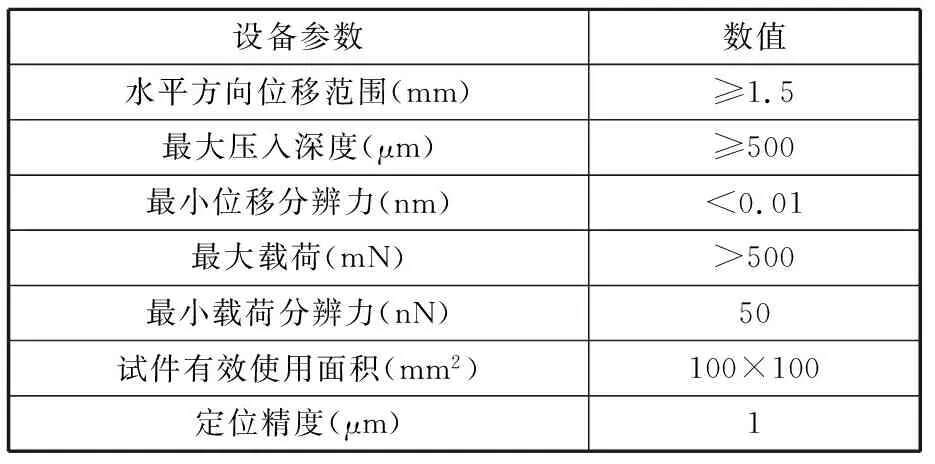
表1 G200型纳米压痕仪设备参数

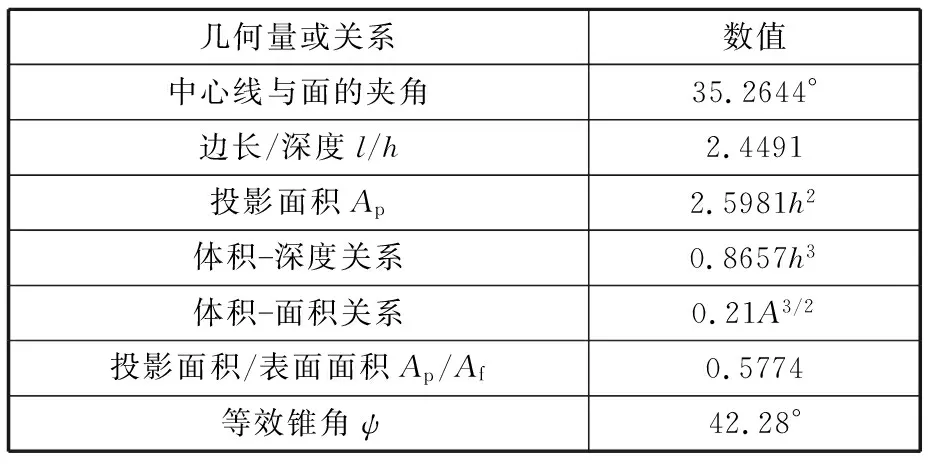
表2 Cube金刚石压头几何参数

3.2 试验步骤

试验前使用丙酮超声清洗样件，去除表面的污渍，然后用氮气枪将其吹干。用Cube金刚石压头代替单颗磨粒对试样进行刻划试验。施加的线性载荷为0～120 mN。压头棱线位于沿刻划方向磨粒轴对称平面内。划痕长度为400 μm，刻划速度为10 μm/s。刻划试验结束后用扫描电镜观察样件表面形貌，然后用腐蚀液对样件表面腐蚀5 min，使裂纹充分暴露。腐蚀以后重新用扫描电镜对其表面形貌进行观测，并记录下来，做三次试验取平均值。根据压痕仪提供的试验数据，用Origin软件绘制氧化镓(010)面线性载荷划痕曲线。

3.3 试验结果

刻划试验完成以后，G200型纳米压痕仪会实时记录下刻划过程中的压入载荷、深度以及划痕长度等数据，通过这些数据绘制变载荷划痕曲线，随后，用形貌仪对划痕表面进行观测，得到划痕的表面形貌图，变载荷划痕曲线及划痕形貌见图7。从图7中可以看出，脆塑转变临界深度在415 nm处，与宋放[14]的试验结果高度一致。分别在图7中选取a、b、c、d、e、f共6个区域进行径向裂纹偏转角的观测。6个区域的压头压入深度分别为110，300，500，680，815，1100 nm。不同压入深度下晶体表面划痕的SEM图见图8。

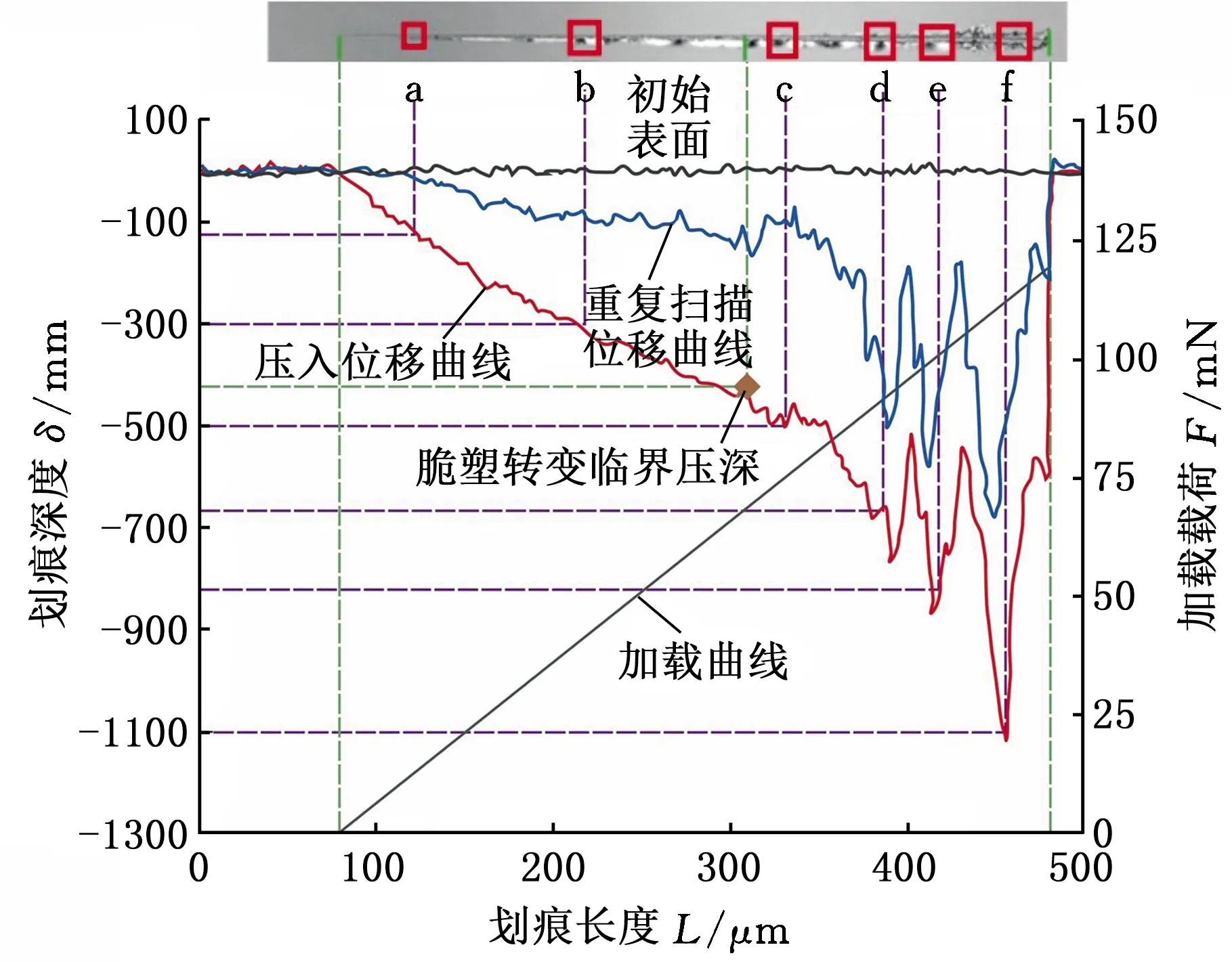
图7 变载荷划痕曲线及划痕形貌图

在图8中，a、b区域压头切削深度分别为110 nm和300 nm，小于脆塑转变临界切深，SEM划痕表面径向裂纹的偏转角在33.5°～35°之间，与MATLAB计算出的解析值33.37°有较高的一致性；c、d、e、f区域压头切削深度分别为500，680，815，1100 nm，大于脆塑转变临界切深，SEM划痕表面径向裂纹的偏转角在38.5°～51°之间，并且随着压头压入深度的增大，径向裂纹的扩展角也增大。当材料发生脆性断裂时，裂纹的偏转角在51°左右，与MATLAB计算出的解析值51.448 62°高度一致。

(a)压头压入深度110 nm (b)压头压入深度300 nm (c)压头压入深度500 nm

4 结论

(1)本文根据弹性力学和断裂力学原理，构建了单颗磨粒刻划氧化镓(010)晶面过程的弹性应力场模型，分析了在被刻划面上的弹性应力场分布的解析表达式。在此基础上，通过MATLAB计算出径向裂纹的成核位置以及裂纹扩展方向，与氧化镓晶体纳米刻划试验结果具有很高的一致性。

(2)在单颗磨粒刻划氧化镓晶体过程中，当压头切削深度不超过脆性转变临界切削深度时，氧化镓晶体以塑性的方式被去除，材料表面未出现明显的脆性断裂，因此，这种情况下不会出现中位裂纹与横向裂纹，存在Blister应力场。试验数据和计算结果都显示出：此时的径向裂纹成核位置在磨粒的后方，裂纹生成方向与刻划方向之间的夹角在33°左右。

(3)当压头切削深度超过脆性转变临界切削深度时，氧化镓晶体以脆性破碎的方式去除材料，中位裂纹将在磨粒尖端下方的塑性变形区边界处萌生，而中位裂纹的萌生和扩展将会削弱或消除由塑性变形引起的Blister应力场，最终可能导致径向裂纹只受法向载荷和切向载荷所产生的应力场的影响。试验数据和计算结果都显示：此时的径向裂纹成核位置进一步向磨粒后方移动，裂纹生成方向与刻划方向之间的夹角在51°左右。

(4)在单颗磨粒线性加载刻划脆性氧化镓晶体过程中，径向裂纹偏转角随着载荷的增加而增大，径向裂纹偏转角在33°～51°之间。