汽车后桥准双曲面齿轮搅油损失数值模拟及其减阻研究

黄丰云，刘伟腾，邹 琳，任良顺

（1.武汉理工大学机电工程学院，湖北 武汉 430070；2.上汽通用五菱汽车股份有限公司，广西 柳州 545000）

1 引言

公司后桥主减速器被动锥齿轮与差速器壳采用螺栓连接紧固，螺栓头裸露在差速器壳法兰面外，工作时螺栓头会间断性地搅动润滑油，从而产生类似“划桨”形式的阻力矩，导致搅油损失，传动效率降低。因此，研究齿轮搅油损失机理并探究减阻方法具有降油耗应用价值。

目前，国内外广泛采用CFD数值方法来研究齿轮搅油损失。文献[1]建立了齿轮箱二维流场模型，分析了齿轮转速、润滑油黏度及浸油深度对内部流场的影响。文献[2]建立了油浴润滑齿轮箱的三维流场模型，分析了旋转方向对流场的影响。文献[3]采用滑移网格技术建立了圆柱齿轮对的三维流场模型，研究转速、温度及浸油深度对搅油损失的影响。文献[4]采用齿面移动法建立了驱动桥飞溅润滑流场模型，分析了内部流场分布及搅油功耗。文献[5]提出了一种基于CFD和响应面法的搅油损失优化模型。现有研究主要针对结构简单的圆柱齿轮、齿轮箱，很少研究结构较复杂的后桥准双曲面齿轮的流场分布及搅油损失。

忽略浸油深度较低的主动锥齿轮、轴承，建立包括被动锥齿轮及差速器壳等旋转部件的后桥三维流场模型。研究后桥内部流场分布、动压力分布以及转速、温度和螺栓结构对搅油损失的影响规律，提出结构改进方案，最后设计台架效率试验验证。

2 后桥内流场数值方法

后桥内部润滑油流动属于三维非定常不可压缩流动，所述的齿轮搅油数值方法取决于连续性方程和N-S动量方程，控制方程为[6-7]：

式中：V→—流体速度矢量；

ρ—密度；

P—单元上的压力；

μ—流体单元动力黏度；

ρg—微元体重力；

F—其他体积力。

主减速器齿轮旋转搅油导致油-气两相动态变化，因此利用VOF模型计算单元内相体积分数来确定自由面的形状和位置[8]。在VOF模型中，相体积分数满足：αair+αoil=1，其中：αoil、αai r分别为润滑油和空气的体积分数。为了实现对自由面的跟踪，需求解润滑油体积分数的连续性方程[9]：

式中：ρo il—润滑油密度；uoi l—润滑油速度矢量；Sα—源项，默认为0；m+—润滑油汽化的质量，m-—润滑油液化的质量；P1—两相扩散后的压力；PV—汽化压力；C+、C-—经验常数；U∞、t∞—昆兹系数。

由式（3）可得单元各相的体积分数，并对整个单元内各相体积分数进行加权平均，即可得单元平均密度和黏度：

式中：ρ—流体单元密度；可知动量式（2）与润滑油体积分数的连续性式（3）通过式（6）、式（7）相互关联。

后桥齿轮旋转搅油存在湍流现象，可能存在涡旋现象，为获得数值解，添加RNG k-ε湍流模型。该模型通过修正湍流动力黏度来考虑湍流涡旋，且修正了湍流耗散率ε方程，提高了精度。湍动能k及耗散率ε输运方程为[10]：

式中：k—湍流动能；ε—湍流耗散率；ak、aε—k、ε的有效湍流普朗特数的倒数；ak=aε=1.393；μef f—修正后的湍流动力黏度，μeff=μt+μ，μt=ρCμk2/ε，μt—湍流涡黏系数；Gk—由平均速度梯度引起的湍动能的生成项；C1ε=1.42、C2ε=1.68；Rε—RNG k-ε模型对耗散率方程的修正项。

3 准双曲面齿轮搅油损失数值模型

3.1 流域模型的创建

利用UG8.0建立后桥三维模型，忽略浸油深度较低的主动锥齿轮、轴承及差速器齿轮，考虑被动锥齿轮及差速器壳等旋转部件，简化模型。抽取后桥壳和主减速器壳内表面及被动锥齿轮和差速器壳外表面，形成计算域，如图1所示。

图1 后桥流体域Fig.1 Fluid Domain of the Rear Axle

3.2 网格划分及空间离散

利用HyperMesh13.0建立网格模型。由于后桥被动锥齿轮结构复杂且存在动网格边界，为了使网格更适应模型，采用非结构四面体网格单元，并在被动锥齿轮及差速器壳处进行网格局部细化，流体域初始网格单元总数为1366404。为定义边界条件，需对网格模型边界进行分组，如图2所示。采用PISO算法求解连续性方程和动量方程中的压力与速度耦合；空间离散中的压力采用PRESTO!格式离散，其余扩散相采用二阶迎风格式离散；在时间上采用一阶隐式格式。

图2 后桥流域网格划分Fig.2 The Mesh Generation of the Rear Axle Fluid Domain

3.3 材料参数及边界条件

数值模拟润滑油温度和转速对后桥被动锥齿轮搅油功率损失的影响，具体影响参数及两相的材料参数，如表1所示。

表1 材料参数及仿真参数Tab.1 Material Parameters and Simulation Parameters

定义桥壳及主减速器壳为固壁无滑移边界条件；后桥两轴端为pressure outlet，出口压力大气压，参考压力为零；编写profile文件定义被动锥齿轮及差速器壳的转速及转向。利用Adapt中的Region Adaption标记出润滑油的初始浸油高度为48mm，仿真初始情况，如图3所示。红色部分代表润滑油，其余为空气。

图3 仿真初始两相分布Fig.3 Two-Phase Distribution at the Simulation Initial

4 数值计算结果分析

4.1 后桥内部流场分布

后桥润滑油因其黏性作用而被后桥被动锥齿轮旋转带起飞溅，从而完成对齿轮、轴承的润滑、冷却，其分布随时间呈现不同的规律。被动锥齿轮以133rpm顺时针旋转时，不同时刻（t=0.1s、0.2s、0.3s、0.4s）后桥内部润滑油分布规律，如图4所示。由图可知，t=0.1s时，被齿约转过90°，带动部分润滑油吸附在被齿表面并沿壁面流动；t=0.2s时，被齿约转过180°，更多的润滑油被带起并开始沿壁面流到后桥顶部，且齿面分布着较多润滑油；t=0.4s时，被齿约转过360°，越来越多流动至后桥顶部及分布在齿面的润滑油在重力作用下，向后桥两侧流动并逐渐滴落回底部油池，从而对主被动齿轮、差速器齿轮及主减支撑轴承进行润滑及冷却，随着时间推移，最终达到一个动态相对稳定的状态。

图4 133rpm时不同时刻后桥流场分布Fig.4 Flow Field Distribution of Rear Axle at Different Moments at 133 rpm

4.2 后桥内部动压力分布

4.2.1 被动锥齿轮动压力分布

不同转速下，被动锥齿轮动压力分布，如图5所示。由图5可知，差速器壳动压力几乎为零，而齿槽齿面动压力较大，这是因为齿槽浸在润滑油中，是主要的搅油部分；齿槽内动压力分布不同，在齿槽齿根处动压力最大。当转速从133rpm提高到888rpm时，被动锥齿轮最大动压力从1464Pa显著增大为23715Pa，表明搅油阻力将随转速增加而显著增大。

图5 不同转速下被齿动压力分布Fig.5 Dynamic Pressure Distribution of the Passive Gear at Different Speeds

4.2.2 被齿螺栓截面动压力分布

不同转速下，被齿螺栓截面动压力分布，如图6所示。随着转速提高，动压力分布的区域从螺栓周围扩大到后桥顶部及底部，甚至在后桥顶部产生旋涡，且螺栓周边区域整体动压力增加，最大动压力从967Pa增大到9739Pa；螺栓背流面产生动压力较高、动压力梯度较大的集中区域（图6椭圆形区域），且随转速提高，集中的高压区域越明显。分析表明转速对后桥动压力分布影响较大且螺栓的存在将导致搅油阻力增大。

图6 不同转速下被齿螺栓截面动压力分布Fig.6 Dynamic Pressure Distribution on the Bolt Section at Different Speeds

4.3 各影响因素下的搅油功率及结构改进

4.3.1 温度与转速对搅油损失的影响

温度、转速对搅油功率的影响，如图7所示。由图可知，当润滑油温度从90℃降低到30℃时，搅油功率缓慢增加，在转速为1065rpm时大约增加了30w；然而搅油功率随着转速的增加急剧增大，当转速从444rpm增加到1065rpm时，在30℃时搅油功率从21W增加到254W。分析表明转速对搅油功率的影响较大，而温度对搅油功率的影响相对较小。

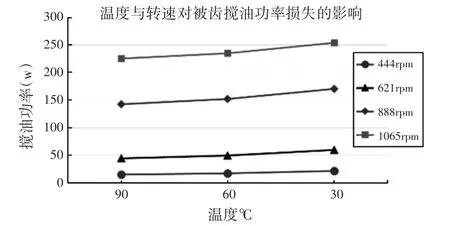
图7 温度与转速对被齿搅油功率损失的影响Fig.7 Effect of Temperature and Speed on the Gear Churning losses

4.3.2 后桥结构改进及其减阻研究

上述分析表明，被动锥齿轮与差速器壳的连接螺栓会产生额外的搅油阻力，因此提出将螺栓连接齿轮改为沉头螺栓齿轮的结构改进方案，如图8所示。

图8 结构改进前后的动压力分布Fig.8 Dynamic Pressure Distribution Before and After Structural Optimization

由图8（b）、8（d）对比可知，沉头螺栓被齿模型可明显减少被齿及螺栓截面的动压力分布，可降低功率损失。

建立沉头螺栓齿轮搅油损失数值模型，并与原模型对比。不同转速下两种模型动压力对比，如图9所示。结果表明在不同转速下，沉头螺栓被齿模型分别降低1.64%、3.72%、1.28%、6.5%、5.97%、2.28%的动压力，可减少搅油功率损失。

图9 不同转速下两种齿轮模型的动压力对比Fig.9 Comparison of Dynamic Pressure Between Two Kinds of Gear Models at Different Speeds

不同转速下，两种模型搅油功率损失对比，如图10所示。结果表明，随着转速提高，搅油功率急剧增大，且在不同转速下，沉头螺栓被齿可分别降低5.76%、7.67%、3.65%、7.94%、6.10%、8.20%的搅油功率，证明结构优化正确。

图10 不同转速下结构优化前后模型的搅油功率损失对比Fig.10 Comparison of the Churning Power Losses Before and After Structural Optimization at Different Speeds

5 台架试验验证

分别对结构改进前后的两种模型进行台架实验，测量其后桥传动效率。实验测试的两种被齿模型，如图11（a）所示。实验台架，如图11（b）所示。包括驱动电机2、传动轴防护罩3、转矩转速传感器1、4和6、后桥样件5及左右半轴端的负载电机。后桥5采用透明后盖，可观察内部流动分布。

图11 实验测试模型及测试台架Fig.11 Experimental Test Model and Test Bench

后桥传动效率η表达式为：

式中：Pin、Pout—输入功率和输出功率；nin、Tin—转矩转速传感器4测得的后桥输入转速、输入扭矩；nout1、nout2—后桥左右半轴端的输出转速；Tout1、T out2—后桥左右半轴端的输出扭矩。在不同的输入转速和输入扭矩下，分别测试两种后桥结构的传动效率。当扭矩为81Nm时，结构改进前后桥传动效率在（95～96）%之间，最高为95.9%，结构改进后（沉头螺栓齿轮）传动效率在（96～97）%之间，最高为97%；当扭矩为135Nm时，结构改进前传动效率最高为96.3%，结构改型后传动效率最高为97.3%，如图12所示。数据表明在不同的工况下，结构改进后（沉头螺栓齿轮）可使后桥传动效率约提高（1～1.1）%，能有效降低搅油损失，实验结果验证了数值仿真和结构改进的正确性。

图12 不同工况下两种后桥模型的传动效率Fig.12 Transmission Efficiency of Two Kinds of Rear Axle Models Under Different Working Conditions

6 结论

建立了包含被动锥齿轮及差速器壳等旋转部件的后桥流场数值模型，研究准双曲面齿轮搅油损失，得出结论：

（1）研究获得不同时刻后桥内部流场分布规律，为后桥润滑油路的优化研究提供了参考。

（2）研究转速、温度及螺栓结构对后桥内部流场分布、动压力分布及搅油功率损失的影响规律。仿真表明：搅油功率随转速的增加而急剧增大、随温度的增加而缓慢减小，其中转速的影响较大；螺栓导致螺栓背流面流场紊乱，形成动压力较高的区域，产生压力梯度力，造成额外的搅油损失。

（3）将螺栓连接被齿改为沉头螺栓被齿，完成结构改进，并设计台架效率实验验证。仿真表明在不同转速下，结构改进后可分别降低5.76%、7.67%、3.65%、7.94%、6.10%、8.20%的搅油功率；实验表明在不同工况下，结构改进后（沉头螺栓齿轮）能使后桥传动效率约提高（1～1.1）%。仿真及实验均表明后桥被齿结构改进是正确的。