MTS∕MTO混合型生产排产决策研究

庞如英，康瑞林

（内蒙古工业大学机械工程学院，内蒙古 呼和浩特 010051）

1 引言

随着客户需求的个性化以及以销定产理念占主导地位等多方面因素的影响，需要企业采取订货生产（MTO，Make-to-Order）方式，同时为了快速响应市场的需求，企业通常又需要采用备货生产（Make-to-Stock，MTS）方式，因此许多企业采用的是二者相结合的MTS∕MTO混合生产模式[1]。

生产调度问题本身就是一个NP难问题，在混合生产中，面对不同生产方式的订单，生产过程随机性、不确定性和复杂性增大，因此使整个控制系统变得更加困难。为了既能缩短MTO订单的生产周期，满足交货期；同时又能使MTS订单保持一定的最优库存量，混合生产排序策略成为混合制生产模式要解决的一个关键问题。目前只有少数学者关注MTS∕MTO混合生产订单排序策略。

文献[2]认为MTO订单带来的收益最大，优先安排MTO订单，并且最大限度地满足MTO订单准时交货；有剩余产能存在的前提下，根据综合值的大小安排MTS、MTS∕MTO订单。文献[3]和文献[1]利用避免饥饿法对订单进行投放，投放模块确保MTO订单按时投放，只有等所有的MTO订单投放完成后才开始投放MTS订单用于填满剩余产能。实际上，他们的模型缺少合理的优先次序，MTO订单被优先投放，而不能在合适的时间投放MTS订单。另外，Chang等和Wu等假设瓶颈设备是已知的，通过瓶颈设备的利用率控制设备负荷。如果混合系统的动态性很高，瓶颈设备的位置会发生转移，不能准确控制所有设备的负荷时，这个假设不成立。订单的动态性和不规则性，使得MTS∕MTO混合生产系统中订单排序变得相当困难甚至难以实现。

文献[4]在混合MTS∕MTO生产背景下构建了层次生产计划结构，其生产排序优先级依次为MTO、MTS∕MTO和MTS。文献[5]为了保证MTO产品能够准时交货，将MTO订单生产优先于MTS订单。文献[6]编制MTS∕MTO混合生产计划时，依据产品的时间紧急度排序优先生产MTO订单，MTS订单依据在制品的数量决定投放顺序。同样，文献[7、8]通过计算MTS和MTO订单的紧急度，确定订单的投放优先级为：紧急MTO>紧急MTS>非紧急MTO>非紧急MTS。Eivazy等在上述排序中遇到队列值相同时，利用最短剩余时间（SRPT）规则来决定优先级。如果数值再次相等时，利用剩余潜在瓶颈步骤中累计加工时间小的订单优先级高。

分析上述文献，所有模型大体上都是优先加工MTO订单，即使文献[7、8]考虑了MTS订单，也只是简单进行了归类，而不符合实际生产，实际上并非所有情况下，MTS订单收益都小于MTO订单，因此现有文献对混合订单投放策略考虑不周全，缺少一种较严谨的科学投放方法。因此，构建了考虑综合收益的订单紧急度，在此基础上，建立动态的MTS、MTO订单排产决策，以缩短订单的加工时间，提高设备利用率。

2 构建基于负荷控制的MTS∕MTO生产控制模型

MTS∕MTO混合生产系统具有极大的随机性，如果订单池中订单投放顺序混乱，就会引起生产系统负荷不平衡，这种不平衡现象会导致瓶颈设备转移。为了解决MTS∕MTO混合生产的动态性和复杂性，运用负荷控制法控制每台设备负荷的上限阈值，确定订单投放时间，将系统负荷（WIP）维持在一定的稳定水平，来有效避免设备闲置或拥堵，以及由交货期等随机因素引起的负荷变化，保证生产有序、最大完成时间最小。

2.1 负荷统计范围的确定

为了将MTO、MTS生产统一建模，将MTS产品也看成一种订单，其客户为库房，订单量为预测量。

负荷度量指标通常分为两种：即加工工件数目和加工时间。由于各设备之间的工作量相差可能甚大，加工工件数目不能精确统计每台设备的负荷，为了准确反映生产系统的负荷变化情况，采用按加工时间法统计车间负荷。

生产系统由订单池、生产车间、加工设备组成，各环节之间的关系以及负荷分布情况，如图1所示。当订单j进入生产系统后，未被投放之前，不消耗生产资源，所以当订单在订单池中等待投放时，形成投放负荷LP；当订单j进入生产车间，投放后尚未到某台设备s的队列，相对某台设备s形成的负荷称为上游负荷LU；直接负荷LD：各设备加工队列的负荷分布情况；集成负荷LF：包含设备上游负荷LU和设备直接负荷LD。由于投放负荷LP尚未消耗生产能力，对设备s的负荷贡献率为0，因此用集成负荷LF控制设备上限负荷阈值。

图1 生产系统负荷分布Fig.1 Load Distribution of Production System

2.2 负荷统计的方法

由于订单随机到达，导致订单优先级排序不断更新，因此每次投放之前和结束之后都要对设备负荷进行更新，确定下一次的投放时机。

常用的负荷统计方法有：折算负荷统计方法（Load Convert⁃ed）、集成负荷统计方法（Aggregate）。文献[9]研究了以上两负荷统计方法，结果显示：Load Converted方法当订单数量过多时，不能精确统计设备负荷；而Aggregate方法当订单的工艺路线存在较强主流向时，不太适用。文献[12]提出了一种新的统计方法：修正集成负荷统计方法（Adjusted Aggregate Load），采用该方法统计作业车间设备集成负荷时，设备s的负荷不会随着工序的变化进行波动，可以设置固定的负荷阈值，确定准确的投放时机。随机动态MTS∕MTO混合生产模式，依据产品加工工艺路线安排订单工序并做动态调整，采用修正集成负荷统计方法对设备负荷进行统计。

设备s集成负荷LF为：

式中：Pjs—订单j在设备s上的加工时间；

n js—订单j在设备s上加工的工序号。

此种统计方法按照订单j首道工序与设备S的距离进行折算，距离越远负荷贡献越小，距离越近负荷贡献越大。

通过设备s集成负荷与设备s最大负荷差值控制设备负荷上限阈值，据此确定订单投放时机。

Ns为设备的最大负荷；

当Ns>L F：设备s集成负荷未达到设备s最大负荷阈值上限，此时可以继续投放订单；

当Ns=L F：设备s集成负荷满足设备s最大负荷阈值上限，此时保持当前现状即可。

2.3 负荷控制的投放方法

按投放驱动的方向来分析，投放方法分为：拉式投放（PULL），当设备负荷降到负荷阈值下限时，投放模块立即启动；推式投放（PUSH），在合适的投放时间点，按优先次序将待投放订单依次“推”向车间，并保持车间各设备负荷满足投放要求。

由于PULL方法优先投放紧急订单，促使急单顺利进入生产车间，当各工位负荷不均衡时，PULL方法影响投放时间的准确性。而PUSH方法不会出现订单滞留现象，订单到达时直接进入首道工序队列，但忽视了急单的处理而产生过多的拖期订单。为了合理有序的投放订单，将两种投放方法相结合，构建推拉混合投放方法。混合投放方法的投放规则如下：

（1）初始工序按拉式投放，当设备闲置时开始工作。

（2）其它工序按推式投放。

3 投放策略的确定

订单投放主要研究采用什么样的策略将一定数量的订单在适当的时间从订单池投放到生产线。主要内容是：

（1）确定订单池中待投放订单的投放优先级。

（2）确定订单投放时机。

订单动态排序过程中投放模块同时并持续完成这两项内容。首先，确定订单池中投放订单的优先级和队列。然后依次检查所有订单的投放条件，只要满足投放要求，订单池中就会形成一系列满足投放条件的订单，称为可行集。最后，可行集中订单按优先级排序，逐个检查每个订单的投放可行性，直到可行集中所有订单被投放为止。

3.1确定MTO和MTS订单综合投放优先级

已有研究文献对订单紧急度的确定，只关注了交货期属性，而在企业实际操作中还会考虑到订单的利润、工艺复杂性等。因为MTO订单的个性化需求高，加工工艺比较复杂，但给企业带来巨大的收益和发展潜力；而MTS主要生产大众化产品，工艺过程相对比较成熟简单，成本低，但MTS生产需要进行备货，相对于MTO生产占用了大量流动资金。故将综合交货期、利润、工艺复杂性确定订单紧急度。

通过上述分析，MTS∕MTO混合生产车间订单池中订单的优先级通过计算MTS、MTO订单的紧急度C R来确定。

式中：Uj—订单j交货期紧急度因子。当订单类别为M TO时，U j=（toj-t）/T j，其中t—当前时间；toj—订单j的交货时间；Tj—订单j的加工周期。当订单类别为MTS时，Uj=Ij∕Dj，其中D j—预计订单j的需求量；Ij—订单j的库存量（包含在制品）。Bj—订单j的工艺复杂性因子，表示订单的工艺复杂度与企业生产资源、工人技术水平的匹配程度。如果企业现有的生产资源、工人技术水平不能满足订单某道工序的工艺要求，这种订单就可以外包或拒绝，采用灰色关联分析理论确定订单的工艺复杂性，为无量纲量。F j—订单j的利润因子；为了统一数量级，且转化为无量纲量，除以10000元。

式中：Pj—订单j的单价；C j—订单j的生产成本；Wj—订单j的机会成本，表示利用一定的时间或资源生产某一订单时，而失去利用这些资源生产其他最佳订单的机会；Hj—订单j的实际交货数量。

α、β、γ：U j、Bj、1∕F j三者的权重系数，用熵值法确定。

由式（2），订单池中MTO、MTS订单的优先级与其紧急度成反比，当订单的交货期紧急度因子越小，工艺较简单，利润越丰厚，订单的优先级越高。通常情况下MTO订单带来的收益相对较高，所以当紧急度相同时，优先投放MTO订单。

3.2 MTO和MTS订单投放时机

在订单池中，按优先级排序确定订单投放队列，基于修正集成负荷统计法实时控制生产线设备负荷，设定投放条件来确定订单投放时机。检查订单池中投放订单的可行性，当设备负荷降为0时，启动投放状态，连续检查订单池中订单的投放条件，以应对车间设备负荷的变动。对于每个投放条件来说，只有不超过设备的负荷阈值时才投放订单，由于MTS∕MTO混合生产会面临多种订单排产，订单投放并不固定在某一个周期，只要当机器的负荷条件满足投放条件开始投放订单，不考虑批量投放生产，只考虑按单个订单投放。订单的投放流程，如图2所示；具体过程如下：

（1）订单池中存在紧急订单：将所有的紧急订单形成可行集，如果可行集中优先级最高的订单投放后不会超过设备的负荷阈值，投放该订单；否则，检查可行集内次优先级订单，重复检查直到可行集内的订单不满足投放条件为止。订单被投放后，更新所有设备的负荷和订单池中订单的优先级。

（2）某设备队列中所有订单都是非紧急订单：为了防止第一台设备闲置，采用推式投放方法。这里可行集包括订单池里的紧急订单，采用上述投放程序检查可行集内订单的投放条件。

（3）某台设备闲置：可行集中订单的第一道工序设备与该设备相关，基于之前的投放程序采用拉式投放法检查可行集内订单的投放条件。这种拉式负荷控制投放法，有利于提高设备利用率，减小订单在订单池或设备队列中的等待时间或者总的完成时间，并且使设备负荷保持平衡。

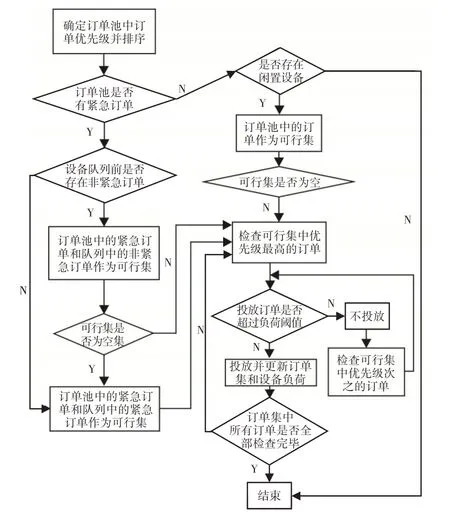
图2订单投放流程Fig.2 Process of Release Orders

4模型求解与仿真分析

某机加车间由9台加工设备组成，每台设备只完成1道工序，各设备的生产能力，如表1所示。该车间目前共接收了6份订单，各订单生产信息，如表2所示。

表1设备生产能力（单位：min）Tab.1 Production Capacity of Each Machine（min）

表2订单生产信息Tab.2 Production Information of Each Order

这6份订单分别要求按照事先规定好的工艺顺序，在指定的机器组上完成，如表3所示。其中括号内的数字为工序所使用的设备号。

表3 订单加工工序所用的加工设备及加工时间（单位：min）Tab.3 Processing Time and Machine of Order Craft Route（min）

4.1 模型求解

混合生产排序问题是组合优化问题，是NP难题。求解这类问题主要采用启发式算法。遗传算法是一种全局优化概率搜索算法，可以快速搜索可行解中的全体解，而不会陷入局部最优解的陷阱；并且利用它的内在并行性，可以进行分布式计算，加快求解速度，通常用于求解复杂调度问题[10]。运用Matlab软件采用遗传算法对上述模型进行求解，各参数设置如下：NIND=40（种群大小），MAXGEN=50（遗传代数），P-Cross=0.89（交叉率），P-Mutation=0.6（变异率）。

采用基于工序进行编码，易于与GA进行结合。由n个工件，每个工件包含m道工序组成的订单群，基于工序进行编码形成n×m个表示工序的基因染色体，每个基因仅表示工序的先后约束，不表示具体的某道工序。采用最大加工时间最小化为适应度函数确定种群规模，将互换变异与逆转变异相结合进行变异操作。适应度函数：

式中：f（x）—最大完成时间；c—目标函数界限保守估计值；由于最大完成时间一个正值，所以令1+c=0，则适应度函数为：

采用灰色关联分析理论确定每份订单的工艺复杂度系数；熵值法确定了紧急因子、利润、工艺复杂度分别对应的权重为αS=0.29、βS=0.38、γS=0.33；αO=0.41、βO=0.20、γO=0.39；最后根据公式（2）计算每份订单的紧急度，如表4所示。

表4 订单优先权系数表Tab.4 Priority Coefficient of Each Order

按订单紧急度由高至低排序，根据推拉混合投放方法，确定订单的投放序列为6-2-4-3-1-5，执行先进先出（FIFO）调度规则，订单调度甘特图和解的变化，如图3所示。遗传算法通过15次迭代找到问题的最优解，并且趋于稳定，该方法完成所有的订单只需4550mins。

图3 订单调度甘特图及解的变化Fig.3 Gantt Chart and Change of Junction

图3中，各矩形条上：第一个数字表示订单序号，后两位数字表示工序号。比如“201”表示订单2的第一道工序。

4.2 模型有效性分析

为了验证这里提出投放方法的有效性，以现有MTS∕MTO混合生产排序文献提出的投放策略作为参照，验证提出的投放方法（投放方法A）的有效性。投放方法B：按优先投放MTO订单，全部MTO订单投放完后再投放MTS订单，确定订单的投放序列为4-6-5-1-2-3，订单调度甘特图和解的变化，如图4所示。

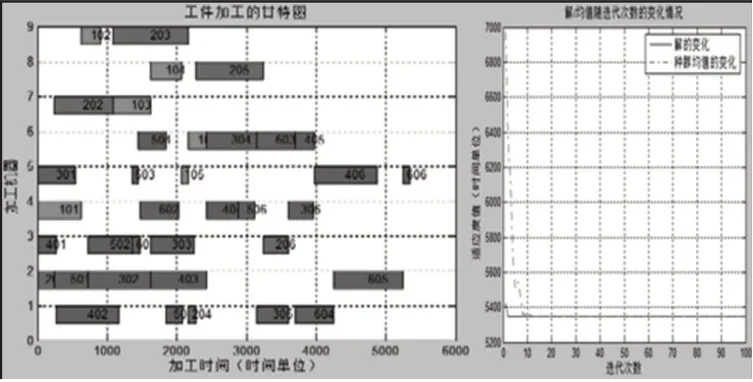
图4 投放方法B订单调度甘特图及解的变化Fig.4 Gantt Chart and Change of Junction of Delivery Method B

投放方法C：按紧急MTO>紧急MTS>非紧急MTO>非紧急MTS优先级投放订单，确定订单的投放序列为4-6-1-2-3-5，订单调度甘特图和解的变化，如图5所示。三种投放方法以最大加工时间、设备利用率作为绩效指标，执行先进先出（FIFO）调度规则。从图3～图5可以得出：投放方法A完成所有订单需要4550min，而采用投放方法B完成所有订单需要5350min，投放方法C需要5050min才能完成所有订单。投放方法A、B控制下订单完成时间趋于稳定，投放方法C控制下订单完成时间波动较大，所以投放方法A能以最短的时间满足交货期。设备利用率由Flexsim仿真得到，结果如表5所示。由表5可知投放方法A设备平均利用率为44.8%，投放方法B、C设备平均利用率分别为38.1%、40.4%，相比之下投放方法A更能有效的利用和平衡设备资源。

图5 投放方法C订单调度甘特图及解的变化Fig.5 Gantt Chart and Change of Junction of Delivery Method C

5 结论

用负荷控制方法构建了MTS∕MTO混合生产控制模型。然后分析了影响MTS、MTO订单紧急度的关键因子，构建了MTS∕MTO混合订单投放排序模型，并用推拉混合投放方法检验各设备的负荷阈值确定投放时间。最后采用遗传算法对该模型进行案例分析，得到所有订单的最短加工时间为4550min，优于现有投放方法B、C的加工时间，分别为5350min、5050min；且设备平均利用率为44.8%，高于投放方法B、C的设备平均利用率，分别为38.1%、40.4%。

该模型综合考虑了影响订单排序决策因素及其之间的重要程度，并将MTS、MTO两种订单统一考虑，更符合企业生产实际。