一种适用于约束空间的拉丁超立方取点策略
杜 丽,吕利叶,孙 伟,宋学官
(大连理工大学机械工程学院,辽宁 大连 116024)
1 引言
复杂机械系统的设计与优化一般需要成千上万次的高保真模型仿真方可完成,这个过程耗时巨大成本高昂,因此基于小样本数据的代理模型技术应运而生,且已广泛应用于工程实际中[1]。试验设计(Design of Experiment,DoE)是代理模型技术中关键的一环,其抽样结果对模型的预测精度与后续优化设计有着至关重要的影响。一个好的DoE方法,既可以减少试验次数,缩短试验时间,又可避免盲目性,迅速得到有效的结果。
常用的DoE方法有[2-4]:全析因试验设计(Full Factorial Sam⁃pling,FFS)、正交试验设计(Orthogonal Design,OD)[2]、均匀试验设计(Uniform Design,UD)[3]、拉丁超立方取样[4](Latin Hypercube Sampling,LHS)等。
LHS是由文献[4]于1980年提出的一种抽样方法,也是目前最受欢迎的抽样方法之一。LHS最重要的特性是其投影特性,即任意两个样本点在任意维度的投影都不会重合,其重要意义在于减少在相同维度的不必要试验。但是,一个好的试验设计应该同时满足投影特性和空间填充性或空间均匀性[5-6]。研究者针对DoE的空间填充性与投射特性进行了诸多研究,发展了基于不同准则的优化的拉丁超立方取样(Optimal Latin Hypercube Sam⁃pling,OLHS)[7-9]。这些准则包括最小Audze Eglais势能准则[7])、最小综合均方误差(IMSE)准则[8],最大熵准则[9]以及最大最小距离准则[5]等。
以上提出DoE方法均只适用于无约束空间,而对于约束空间这些方法均不能直接使用。所以,一些研究者就考虑了设计变量构建的约束条件并提出约束拉丁超立方抽样(Constrained Lat⁃in Hypercube Sampling,CLHS)[10-11]。Petelet等开发了一种考虑不等式约束的LHS方法(CLHS),通过对初始拉丁超立方设计进行置换以满足所需的单调约束,它是CLHS的先驱,但是当两个约束变量的最小边界接近时,其空间填充性能变差。Stinstra等提出了一种针对约束空间的最大最小距离方法,叫做SFDP**法。该方法结合非线性规划求解器CONOPT来解决最大最小设计问题,但其投影性能不理想。
由此提出了一种应用于约束空间的连续局部枚举拉丁超立方取样方法(Sequential Local Enumeration-Based LHS for Con⁃strained Design Space,SLE-CLHS),称为SLE-CLHS策略。SLECLHS策略中涉及LHS理论、最大最小距离(Maximin)理论、连续局部枚举拉丁超立方取样(SLE-LHS)[13],因此在接下来的文章中,将会先介绍经典拉丁超立方抽样、最大最小距离拉丁超立方取点(maximin-LHS),然后详细论述所提出的SLE-CLHS算法,接着利用一个二维及两个三维数值案例对SLE-CLHS方法进行演示,并用空间填充特性与投影特性对SLE-CLHS方法进行评估,最后是结论与展望。
2 LHS、OLHS及Maxmin-LHS抽样
2.1 拉丁超立方抽样(LHS)
LHS方法,也叫做随机LHS,由蒙特卡罗(Monte Carlo)方法演化而来,Monte Carlo方法的主要特点是它的敛散性依赖于独立的随机参数个数,而LHS则完全不同。LHS是一种分层抽样方法,当考虑一维的单个变量输入问题:y=f(x),其中x是一个随机变量。对于有多个随机变量输入,一般的分层抽样需要将输入的样本空间等概率地转化为N个区域,这操作起来是很困难的。此时LHS又是另一种多维分层抽样方法,其工作原理如下:
(1)定义参与计算机运行的抽样数目N;
(2)把每一次输入等概率得分成N,且有:

(3)对每一列仅抽取一个样本,各列中所抽取样本位置是随机的。
相对于单纯的分层抽样,LHS抽样的最大优势就在于任何大小的抽样数目都能容易地产生。至于估计均值,通常的做法是:

一般情况下,这种估计的标准误差并没有对标准蒙特卡罗抽样方法进行任何改进,但实际上,LHS对均值和方差的估计和Mon⁃te Carlo方法相比,在效果上至少是一样的,且常常会显著改善。
2.2 优化拉丁超立方抽样(OLHS)
最优化拉丁超立方(Optimal Latin Hypercube Sampling,OL⁃HS)是一种典型的“充满空间”(Space Filling)试验设计,该方法能很好地应用于复杂系统仿真试验的试验设计问题。产生OLHS分布点的优化准则有很多,比如最大熵准则[9]、中心偏差准则[12]、最大最小距离和最小最大距离准则[5]等。LHS利用随机抽样得到试验设计的点,与OLHS的区别在于抽样点的分布不同。OLHS的点的分布更加结构化,优化出来的点的分布更加均匀。但是OLHS比LHS更耗时,比如:一个试验设计有5个设计变量,10个样本点,那么将会有6*1032个可能的分布方案,这显然是不可能的,因此需要一个更加高效的方法在设计空间中搜索,接下来介绍的最大最小距离准则(Maximin)就是一种行之有效的方法。
2.3 最大最小距离拉丁超立方(Maximin-LHS)
相对于其他的抽样方法,Maximin-LHS主要有三方面的主要优势。首先,Maximin-LHS可以在不耗费过多的计算成本的前提下用来产生任意数量的样本点,且Maximin-LHS在模拟实验中是参数化的,非常适合于数值仿真;其次,Maximin-LHS在减少抽样点误差的均值与方差方面表现良好;最后,Maximin-LHS可以较好的保证样本点的空间填充性能与投影性能。对比了Maximin-LHS和随机LHS的取点情况,如图1所示。可以明确看出随机LHS可能出现所有样本点都位于对角线上的情况,虽然这照样满足抽样方案的投影性质但填充性能很差,而Maximin-LHS却能较好的填充整个空间,均匀分布在可行域内。

图1 最大最小距离LHS分布和常规LHS的糟糕分布Fig.1 Maximin-LHS Sampling and Terrible LHS Sampling
Maximin准则可以理解为最大化样本点之间的最小距离,如式(3)所示。

式中:d(xi,x)j—两个样本点xi,xj之间的距离:

文献[6]最先提出基于退火理论的Maximin准则,对于一个给定的试验设计,通过对内部点与点距离d(ij1<=i,j<=n;1<=t<=2>)的排序,会产生一个索引序列(J1,J2,…J)s,式中di代表不同的距离值d1 式中:p—正整数,如果p值太大将会影响后续的分布。也将采用ϕp准则用于后续研究。 SLE-CLHS算法考虑了样本变量之间的约束,可直接用于约束设计空间的可行域采样。在采样过程中先剔除不满足约束条件的点,然后在可行域中产生新的点,新点在约束空间中继续搜索,直到该点达到满足整体抽样的空间填充性和投影性。SLE-CLSH的采样过程如下: 当用Maxmin-LHS算法在无约束设计空间中产生m个样本点时,落在可行域之外的点是无意义的,应予以消除。为了解决这个问题,可以考虑将这些无用的点移动到可行域中,或者删除这些点,然后在可行域中重新生成。假设在二维设计空间中产生m个样本点,m个样本点中有t个点满足约束条件,其中t 为了重新生成新的点,强调了两个不可忽略的方面,即投影性和空间填充性。 (1)投影特性:为了在所有维度上满足这一特性,以x1轴为基准方向。选择上述最大距离值所在的相邻两点,并将第t+1个点沿x1方向放置在这两点的1∕2处,同时在D中重新排列d′,重新生成新的距离集。重复这个过程,直到所有剩余点在X1方向上都被固定,其中接下来,确定这些新点在x2轴方向上的坐标,具体过程如下。 (2)空间填充性:确定点在x2轴方向的坐标时,以第t+1个点为例,由于其在x1方向的坐标已经确定,在x2方向上以步长λ搜索从0到约束边界的最佳位置。在每次迭代中,计算特征值,特征值是待定的可能采样点与前面已经产生的样本点之间欧式距离的最小值。然后在可行域的x2轴方向上选择最大特征值所在的位置。因此,该位置是x2轴方向上的点t+1的坐标。此时点t+1的位置已经确定Xnew={X1,X2,…,Xt,Xt+1},重复这个过程直到所有的点都被固定,X得以更新Xnew={X1,X2,…,Xt,Xt+1…Xm}。 SLE-CLHS算法的n维(n>2)采样过程与二维类似,都能较好地满足空间填充性和投影特性。 SLE-CLSH策略可用一个实例来详细演示运行步骤。 假设要在二维空间可行域内产生5个样本点,可行域的数学表达式为: 则用SLE-CLSH的采样过程可以详细描述如下: 用maxmin-LHS方法在整个空间内产生5个样本点。 由图2可以看出,点p2和p4落在了可行区域外部。 图2 用MaxminLHS方法在空间取5个样本点Fig.2 Sampling 5 Points by MaxminLHS 由于p2和p4为无效点,所以将其删除,并将要在可行域内产生2个新点p′2和p′4,这两个新点要充分满足试验设计抽样的空间填充性和投影特性。首先,计算点与点间的横坐标间隙。由图2可知,从左边界至右边界,点的横坐标间距分别为1.5、1、2和0.5,所以为了满足投影特性,将第一个新点p′2定在点p1和p3的1∕2处,横坐标3.5的位置,接下来确定该点在下一维度的位置。 (3)现已得p′2的横坐标为3.5,对于纵坐标的位置,我们从纵坐标为0到可行域边界区间,以步长λ进行搜索,在每一步搜索中计算该位置的特征值,直至搜索完毕后,取特征值的最大值所在的位置为p′2点所在的纵坐标的位置。上文已经提到,特征值为该位置与已经产生的样本点之间的欧式距离的最小值。 (4)重复步骤(2),(3)中p′2点的确定过程,可得到p′4点在该可行域内的位置。如图3所示。 图3 用SLE-CLHS方法在可行域内取5个点Fig.3 Sampling 5 Points in Constrained Space Using SLE-CLHS Method 本节分别给出了SLE-CLHS算法在二维和三维设计空间的三个数值实例,案例中的约束都是正则凸约束。 式(7)定义了这个例子的设计空间。 它的可行域实际上是一个具有组合线性约束的不规则区域。如果要在可行域内产生5个样本点,常规方法,如图4所示。该方法消除了三个不满足条件的点,剩下5个点。对于新方法,直接使用SLE-CLHS方法在可行域中产生5个样本点,如图5所示。参数x1在水平轴上绘制,参数x2在垂直轴上绘制。用LHS和SLE-CLHS方法进行采样的样本点的Φ值的比较,如表1所示。可以看出SLE-CLHS方法在可行域所得到的Φ值比常规的方法小,即样本点在可行域的分布更加均匀。 图4 随机LHS方法在可行域内采样Fig.4 Normal Sampling in Constrained Space 图5 SLE-CLHS算法在可行域内采样Fig.5 SLE-CLHS Sampling in Constrained Space 表1 SLE-CLHS和LHS两种取样方法的Φ值比较Tab.1 Comparison of SLE-CLHS and LHS onΦ 对于规则的三维可行域,在此以三维球体的1∕8空间为例,如图6所示。 图6 用常规方法和SLE-CLHS方法在1∕8球体内采样Fig.6 Sampling in 1∕8 Sphere Space by Normal Method and SLE-CLHS 这是一个规则的设计空间,根据图6所示的曲面约束空间,分别用常规的Maxmin-LHS抽样方法及SLE-CLHS方法取10个样本点。约束空间表达式,如式(8)所示。 由图6可以看到,用常规的Maxmin-LHS抽样方法所抽取的10个样本点中,只有5个样本点落在可行域内,这就造成了取样时间的浪费,以及试验盲目性,不能迅速得到有效的结果。 而SLE-CLHS方法取的10个样本点全部位于三维约束区域内部,并拥有着良好的空间填充性和投影特性,能同时节约取样时间和得到精确的样本点数目,并且有良好的取样效果。 但是在实际的工程应用中,变量之间的耦合更多是多变的,所形成的可行域也是不规则的,这也给约束试验设计方法的研究带来了很大的挑战。在此以三维空间的不规则可行域为例进行样本点选取。三维的不规则约束空间中,凸约束边界条件为: 分别用常规的Maxmin-LHS抽样方法及SLE-CLHS方法在可行域内采样产生15个样本点。 由图7可以看到,用Maxmin-LHS抽样方法选取的样本点部分落在了空间可行域外部,很难控制取样个数。而用SLE-CLHS方法的选取结果比较满意,在较好地满足了空间填充性和投影特性的同时,保证了取样效率,降低了试验成本。 图7 在不规则三维可行域内采样Fig.7 Sampling in Irregular Convex Constrained Space 针对现有的无约束空间的取样方法连续局部枚举拉丁超立方取点,提出了一种适用于约束空间的连续局部枚举拉丁超立方体取样(SLE-CLHS)方法。所提出的SLE-CLHS方法重点考虑了样本变量之间的约束,并在这些约束构成的约束空间中进行有效取点。 在设计过程中,先剔除不满足约束条件的点,然后在可行域中确定新样本点的方向,并以一定的步长进行迭代直到达到最优位置。通过3个数值案例对SLE-CLHS方法进行演示与验证,并利用maximin准则的量化值ϕp,与随机LHS进行取样对比,结果表明SLE-CLHS能取得更小的ϕ值,说明SLE-CLHS取得的样本点比随机LHS取得的样本点具有更好的空间填充性能和投影性能,且SLE-CLHS方法能够在约束空间中进行有效取点。 SLE-CLHS方法仍存在一定的不足,如在低维设计空间和样本点个数较少的情况下性能优异,但是随着维度和样本点数增加,其采样效率会相应降低。在以后的工作中,将对所提出的SLE-CLHS算法进行改进,提高其取样效率,使其能够高效便捷的运用到更高维空间中。
3 SLE-CLHS算法
3.1 SLE-CLHS算法的概述
3.2 SLE-CLHS算法的实例演示
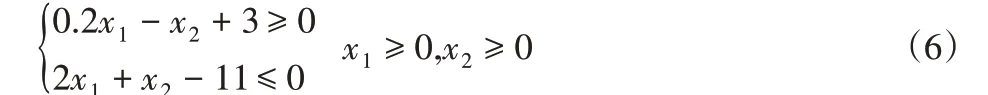


4 数值案例
4.1 二维空间的正则凸约束




4.2 三维球体的1/8约束空间
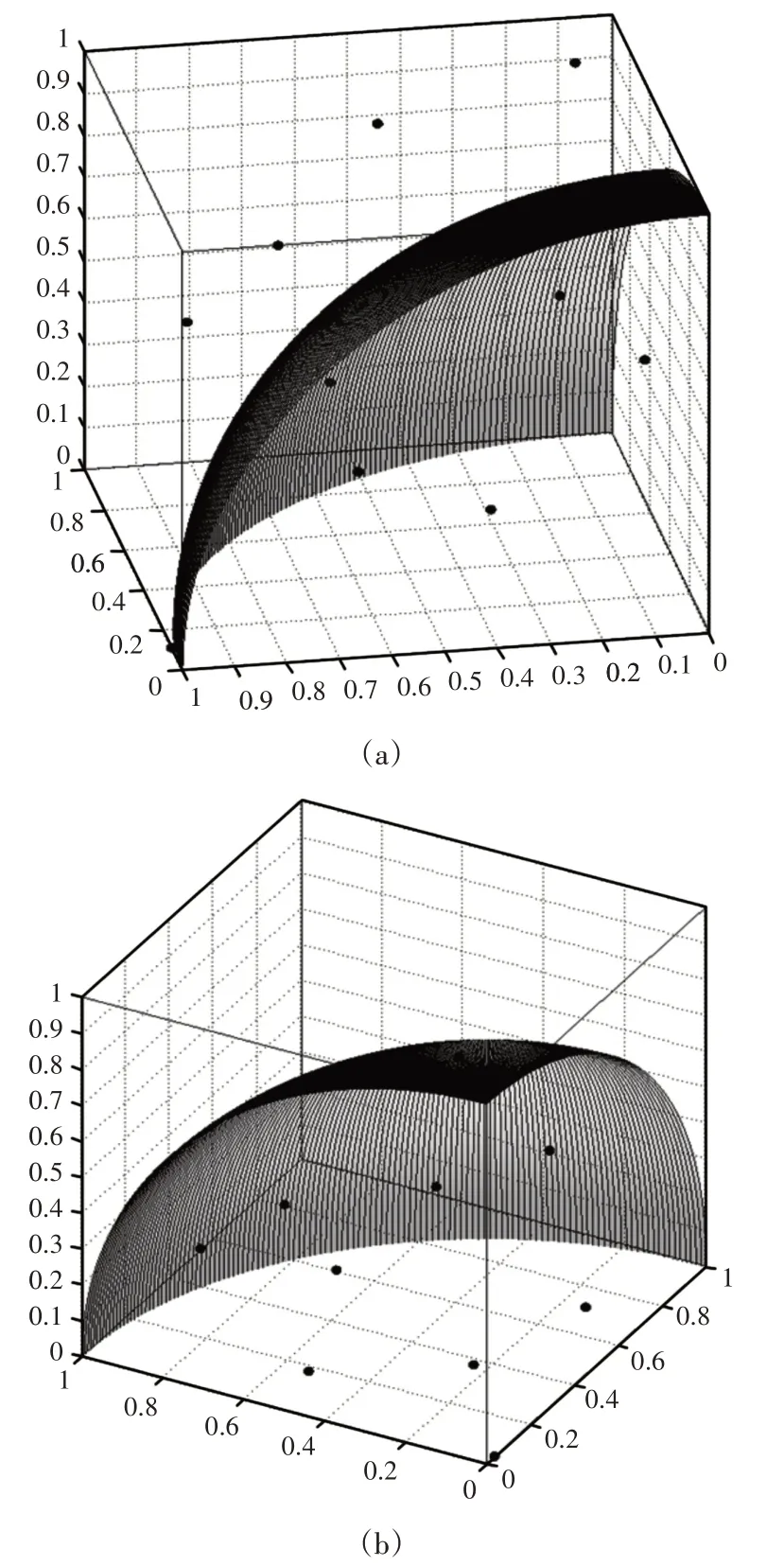

4.3 三维空间的不规则凸约束


5 结论

