基于Retinex理论与局部灰度信息的图像分割方法

崔 强，闵莉花，石又新

1.南京邮电大学 理学院，江苏 南京 210023

2.北方信息控制研究院集团有限公司，江苏 南京 211153

图像分割是利用图像的特征信息将图像划分成多个区域，进而提取出有意义的目标区域。现今，医学图像在医疗诊断过程中具有重要的作用，但是由于光照和成像设备的影响，使得医学图像出现灰度不均匀性，这给医生做出正确的诊断造成了一定的干扰。为了提高医学图像的可读性，使医生可以更有效地观察和诊断，进行有效地医学图像分割具有重要的意义。

图像分割技术经过多年的发展，涌现出了大量的研究成果，学者们提出了各种变分方法［1－6］来进行图像分割，主要有基于边缘的方法和基于区域的方法。基于边缘的方法，是通过利用图像的梯度信息将轮廓移动到目标边界来进行图像分割，例如蛇模型［7］、经典GAC模型［8］和GVF蛇模型［9］。这些模型可以获得较好的分割效果，尤其是对于具有强边界的图像。但是，其分割结果对噪声和初始轮廓线比较敏感。基于区域的方法旨在通过在每个区域中使用全局图像信息进行分割。它们对于初始轮廓具有鲁棒性，并且对强噪声和弱边界的图像可以获得更好的分割效果。然而，大多数基于区域的模型都假设图像灰度均匀，因此无法很好地分割不均匀图像，例如经典CV模型［10］、Mumford-Shah模型［11］及其称为Cai模型的凸变分模型［12］。

在过去的几年中，利用局部灰度信息的方法［13－18］得到广泛发展，并且能有效地提高图像的分割精度。例如，Li等［19－20］通过将局部图像信息引入基于区域的主动轮廓模型的能量泛函中进行图像分割，提出了一种局部二值拟合（LBF）方法。LBF模型可以有效地分割灰度不均匀的图像，但是分割结果对初始轮廓非常敏感。后来，Li等［21］假设偏移场是局部常数，提出了一种新的变分水平集模型（Li模型），该模型利用局部灰度聚类标准函数来评估每个像素附近的偏移场。Li模型对初始化更加鲁棒，并显示出很好的图像分割和偏移校正能力，但迭代过程中过多的卷积计算会降低分割速度。另外，为了获得更理想的分割结果，结合局部和全局灰度信息的方法已经引起了更多的关注，例如文献［22－24］。

此外，近年来众多学者提出了一些基于Retinex的方法［25－27］进行图像分割。根据Retinex理论，灰度不均匀的自然图像可分为分片光滑的偏移场和分片常数的反射（结构）部分。基于Retinex理论，Zosso等［27］提出了一个CVB模型，并建立了一种快速算法，通过使用交替最小化方法和阈值动力学技术对模型进行数值求解［28－29］。该模型可以有效地校正偏移场并获得所需的分割结果，但在目标物体的尖角处CVB模型的分割精度不够好。CVB模型仅考虑了偏移场的光滑性，校正后的图像中并未完全消除偏移场，这严重影响了其分割的精度。最近，Jin等［25］提出了一种新的变分模型（Jin模型）用于图像分割和偏移校正。Jin模型考虑了结构部分的分段常数特性，将全变分项引入CVB模型以校正和分割输入图像，从而获得相对精确的分割结果。

本文提出一个新的两阶段图像分割方法。在第一阶段，考虑到反射部分的光滑性，提出一个基于Retinex理论的变分模型，用来获得图像的结构部分。在第二阶段，将第一阶段获得的结构部分作为输入图像，考虑到偏移场的局部常数特性，提出全变差的图像分割模型，获得比较精确的分割结果。此外，通过使用交替极小化方法，设计了一种有效的算法对模型进行数值求解。最后的数值实验表明，本文提出的两阶段分割方法与已有的CVB模型［27］、Cai模型［12］、Li模型［21］和Jin模型［25］相比能够得到更准确的分割结果。同时，本文模型不依赖初始轮廓线的选择，并且对合成图像，医学灰度不均匀图像等均能进行有效地分割。

1 图像分割方法

1.1 相关模型

给定一副灰度不均匀图像i，根据Retinex理论［30－31］，其可以分解成物体反射（结构）部分s和光照（偏移场）部分b的乘积，即

i＝b·s

通过对数变换I＝lni，B＝lnb，S＝lns，有

I＝B＋S

其中，B一般认为是光滑函数，S为分片常数。

Li等在文献［21］中提出了一种变分水平集方法分割灰度不均匀的图像，该方法统称为Li模型。他们假设偏移场在整个图像区域是缓慢变化的（即：局部常数），并且真实图像的灰度值在不同区域内近似为常数。具体地，Li模型如下

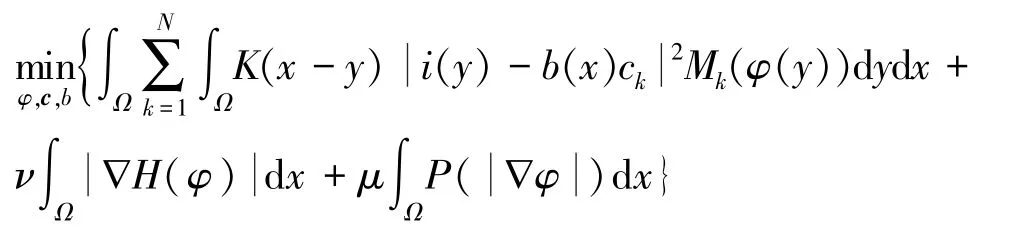
其中，K为截断的高斯核函数

c＝（c1，c2，…，cN）表示不同区域的平均灰度，φ为水平集函数，H（φ）为Heaviside函数，Mk（φ）为区域的隶属函数，函数P（x）＝（x－1）2/2。

2017年，Zosso等［27］基于Retinex理论提出了如下的CVB模型分割灰度不均匀图像

其中，α，λ1，λ2为正参数，u为松弛的Heaviside函数。该模型可以较好地分割灰度不均匀图像，但是对于目标物体的尖角区域，其分割效果不理想，如图1（c）所示。事实上，CVB模型仅考虑了偏移场B的光滑性，矫正图像和分割结果仍然受到偏移场的干扰。

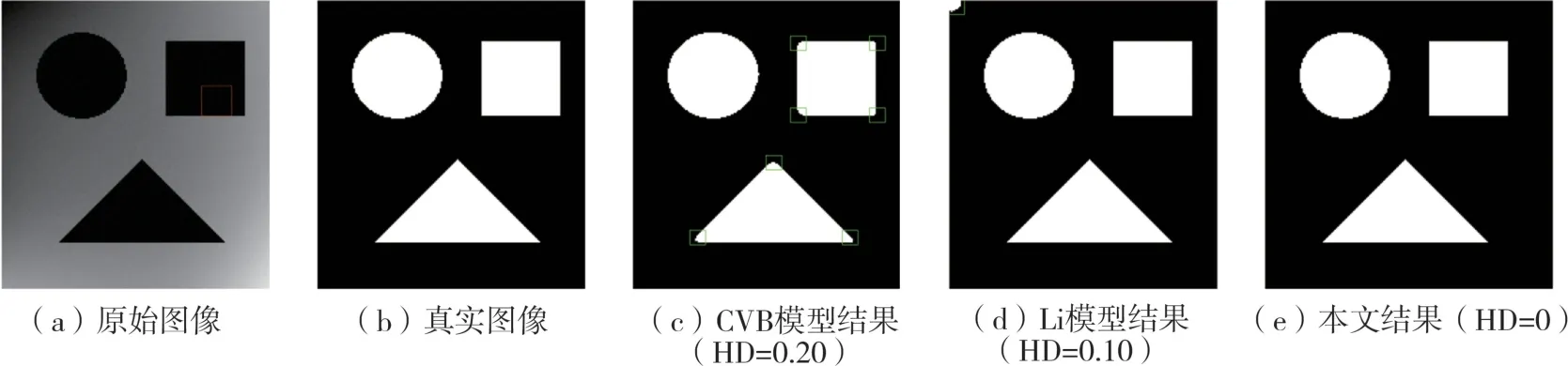
图1 不同模型的分割结果

1.2 本文的分割模型

注意到结构部分S是分片常数，故S∈BV（Ω）［32］。 此外，偏移场B不仅是空间光滑的，而且是局部常数。因此，为了得到更精确的分割结果，本文提出一个新的两阶段图像分割方法用于分割灰度不均匀图像。第一阶段，利用结构部分和偏移场的光滑性，提取图像的结构部分S。第二阶段，利用偏移场的局部常数特性，对提取出的S进行图像分割。具体说来，本文所提的模型如下：

其中

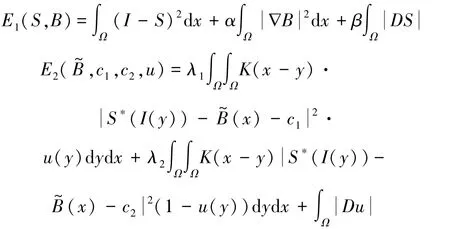
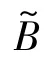
图1给出了本文模型对一个灰度不均匀的简单图像的分割结果。为方便比较，Li模型和CVB模型相应的分割结果也一并给出，并用Hausdorff距离（HD）［33］来定量评估不同方法的分割性能。在图1中，图1（a）是待分割的灰度不均匀图像（初始轮廓线用红色标出），图1（b）是真实图像，图1（c）是CVB模型的分割结果，图1（d）是Li模型的分割结果，图1（e）是本文模型的分割结果。在图1（c）中，CVB模型在目标区域的尖角处（绿色框内）出现了错误的分割结果，其对应的HD值为0.20。观察Li模型的分割结果图1（d），发现在绿色框区域亦出现了错误的分割结果，其对应的HD值为0.10。而本文模型充分利用了图像的各种先验信息，同时考虑了B和S的光滑性，以及偏移场的局部常数特性，因此视觉上获得了比较精确的分割结果（见图1（e）），其对应的HD值也更理想。

2 模型的理论分析及求解算法

2.1 理论分析

由于本文模型第一阶段所提取图像的结构部分S，是第二阶段进一步图像分割的基础，因此第一阶段变分模型的解是否存在是非常重要的问题。事实上，有下面的理论结果。

定理1设Ω⊂R2是具有Lipschitz边界的有界图像区域，I∈BV（Ω），则对固定的正常数α和β，变分问题（2）存在一个极小解。

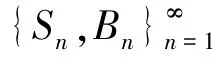
根据定义，存在正常数C，使得E1（Sn，Bn）≤C，即

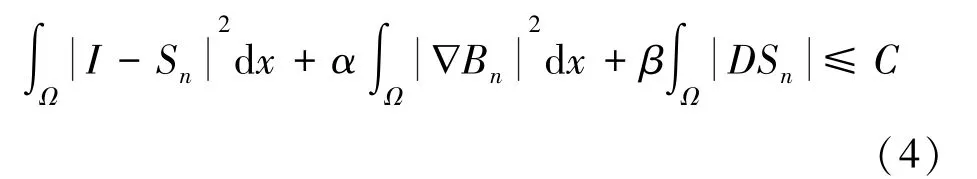
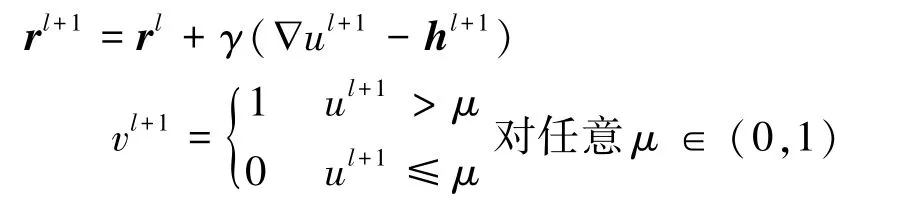
Step7 迭代终止条件‖cl＋1－cl‖＜ε2，停止迭代。

3 数值实验

本节分别对合成图像、医学MR图像和真实图像进行实验，并通过与CVB模型［27］、Cai模型［12］、WLZL模型［26］、Li模型［21］和Jin模型［25］对比，验证本文模型对于灰度不均匀图像的分割性能。本实验的运行环境为：PC机的CPU为Inter（R）Core（TM）i5-4200CPU@2.50 GHz，内存为16 GB，操作系统为64位Win7，Matlab版本为R2015b。本文实验参数选取方式如下：图像I至IV中，β＝5，ρ1＝ρ2＝1，λ1＝λ2＝45，γ＝0.01；图像V至VIII中，β＝6，ρ1＝10，ρ2＝0.5，λ1＝7，λ2＝1，γ＝0.01。 具体地，参数α的取值见表1。

表1 参数的取值

此外，选取量化指标DSC值［35］和HD值［33］作为分割结果的评价标准，其定义分别为

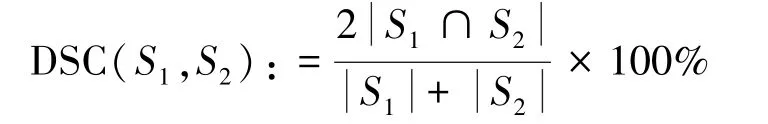
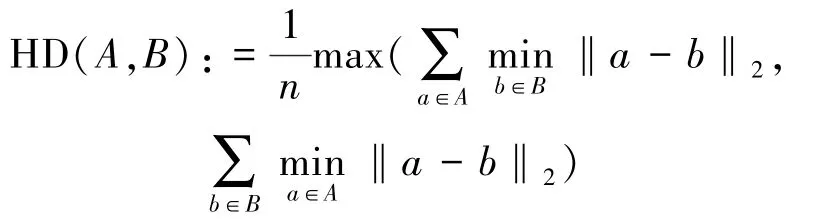
其中，n为目标边界集的总数，A为分割的二值图像，B为二值图像对应的真实图像。HD值越低，表明分割结果越精确。

首先，对一幅合成图像进行分割，并选取4种不同的初始轮廓线验证本文算法对初始轮廓的鲁棒性。图2中，第一行图2（a）是灰度不均匀的合成图像和其对应的真实图像图2（b），第二行图2（c）至（f）是本文算法的分割结果（红色）和初始轮廓线（蓝色），第三行是分割结果对应的二值图像，其HD值全等于0。这些结果表明了该模型对于初始轮廓线的鲁棒性。

图2 本文算法对具有不同初始轮廓线的合成图像进行分割的结果

其次，将本文模型用于分割四幅合成图像。图3中，图3（a）为带初始轮廓线的输入图像，图3（b）至（g）分别为Cai模型、CVB模型、WLZL模型、Li模型、Jin模型以及本文模型的分割结果。对于合成图像，Cai模型、CVB模型和WLZL模型的分割结果不够好，而Li模型、Jin模型和本文模型均能得到精确的分割结果。事实上，通过观察图像I、III、IV，Cai模型和WLZL模型的结果在右下角有明显的错误。对于图像II，Cai模型的分割结果与目标边界之间存在间隙。对于图像I、II、III，CVB模型的分割结果在绿色框区域内欠佳。此外，为了定量地评估不同方法的分割性能，我们在表2中给出各个模型所得分割结果的DSC值和HD值。从表2中可以看到，本文模型、Li模型和Jin模型均得到了最高的DSC和最低的HD值。这些结果证实本文方法可以很好地分割合成图像并得到理想的分割精度。

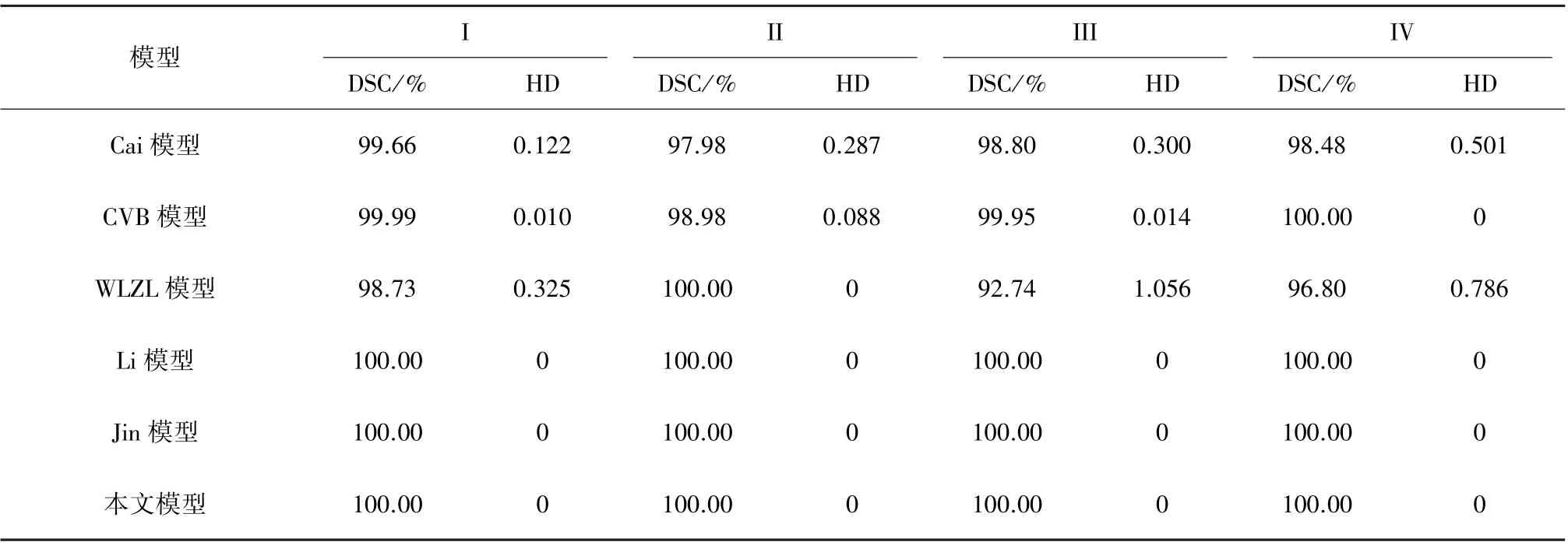
表2 图3中不同模型分割结果的DSC值和HD值比较

图3 不同模型对合成图像分割结果比较

将本文模型用于医学图像分割，并选取四幅脑部MR图像进行比较。图4中，图4（a）为带初始轮廓线的输入图像，图4（b）至（g）分别为Cai模型、CVB模型、WLZL模型、Li模型、Jin模型以及本文模型的分割结果。观察图4，由于脑部图像的白质区域与灰质区域的灰度相似，Cai模型、CVB模型和WLZL模型几乎不能将其分开，Li模型和Jin模型可以将其较好地分开，但在绿色框区域内欠佳，而本文模型能得到更精确的分割结果。表3给出各个模型对于四幅MR图像所得分割结果的DSC值和HD值。可以看出，与其他模型相比，本文模型充分利用了图像的各种先验信息，得到了最高的DSC值和最低的HD值。这些结果表明本文模型对于医学图像分割的有效性。

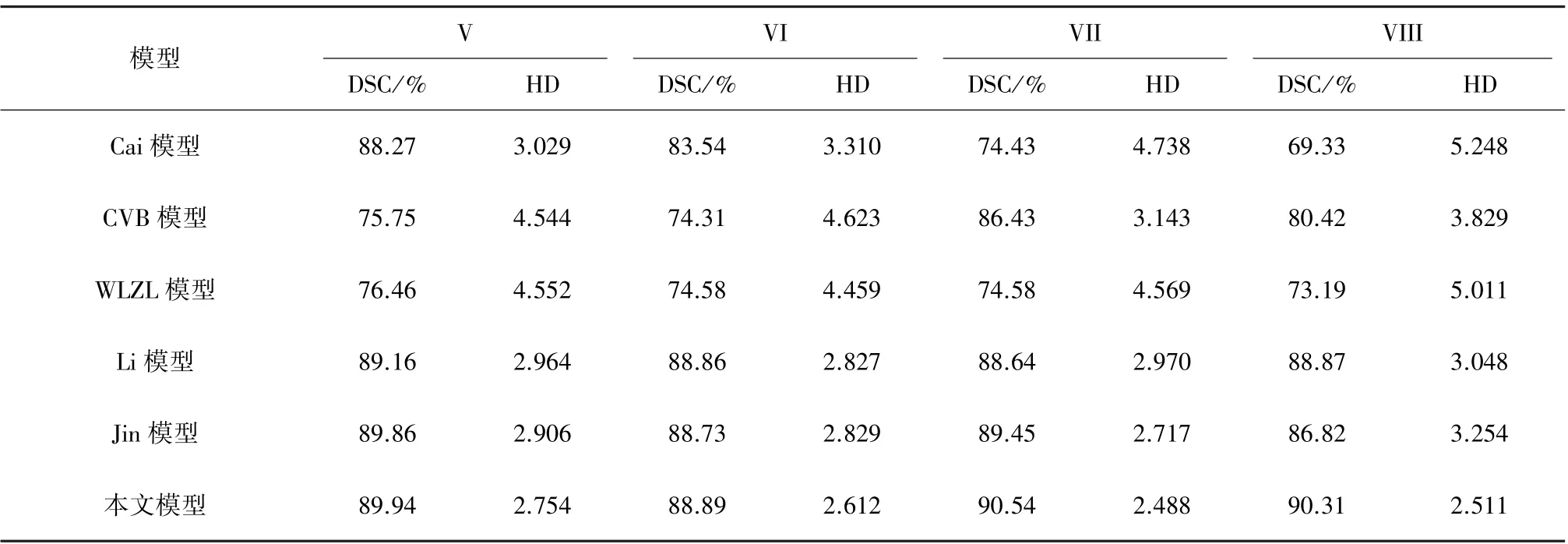
表3 图4中不同模型分割结果的DSC值和HD值比较

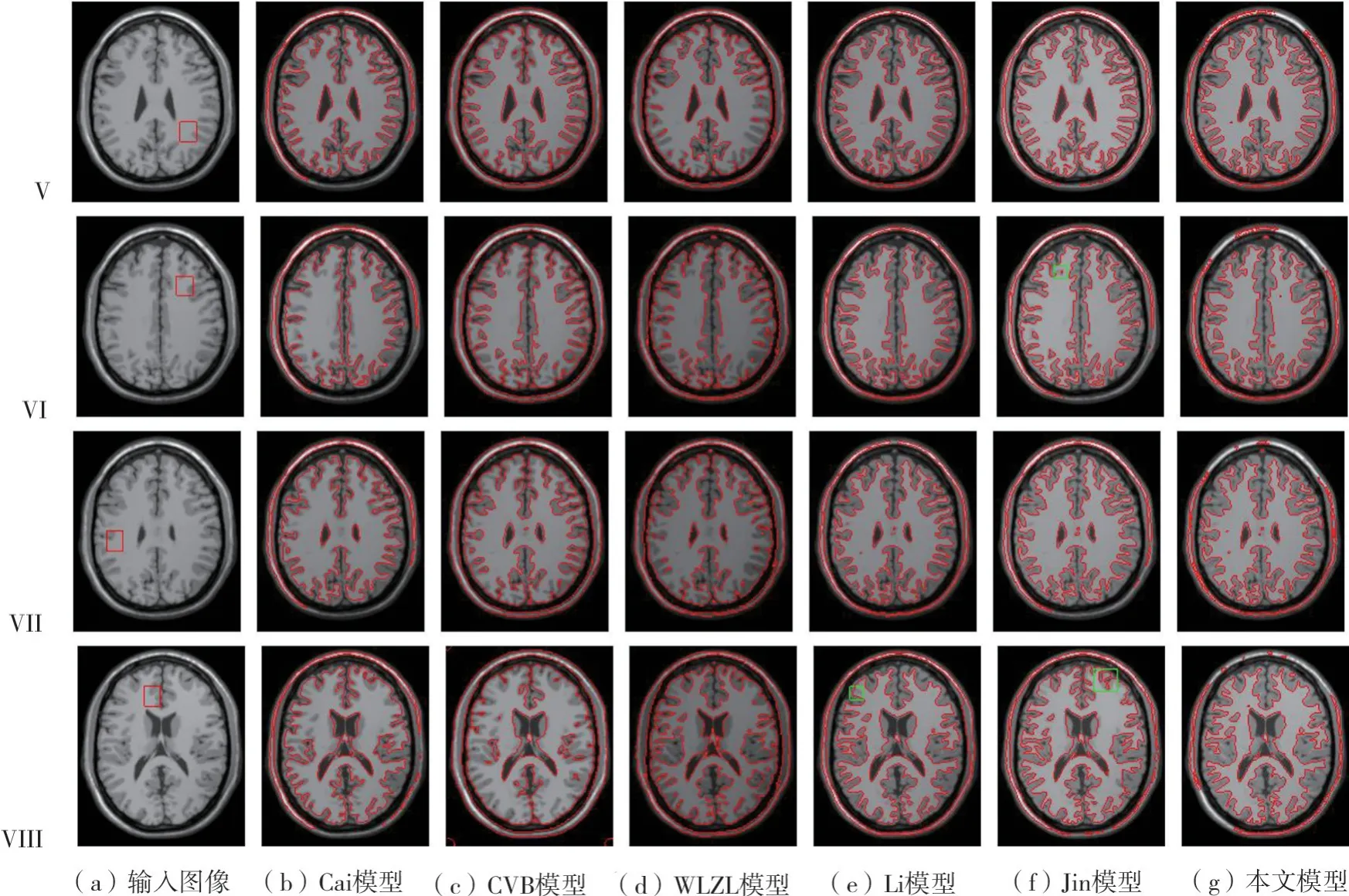
图4 不同模型对MR图像分割结果比较

最后，将本文模型用于分割真实图像。图5展示了四幅真实图像以及各个模型的分割结果，其中图5（a）给出了初始轮廓线（红色）。观察图5，Cai模型和CVB模型对真实图像（IX至XII）的分割结果不够准确。WLZL模型对于真实图像IX的分割结果较好，但是对于真实图像（X至XII）的分割结果不够好。对于真实图像IX、X和XI，Li模型得到了较好的分割结果，但对于图像XII，Li模型的分割结果不准确。对于真实图像IX、X和XII，Jin模型可以分割出目标物体，但对于图像XI，Jin模型不能分割出图像边缘的目标物体。观察图5（g），可以看出，本文模型可以获得较好的分割结果。这些结果表明本文模型对于分割真实的灰度不均匀图像的有效性。

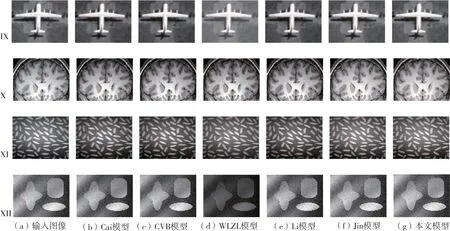
图5 不同模型对真实图像分割结果比较

4 结束语

本文针对灰度不均匀的图像分割问题，提出了一个基于Retinex理论和局部灰度信息的两阶段图像分割方法。论文提出的方法充分利用了图像的结构部分和偏移场的各种先验信息，并且结合了交替极小化方法。通过与已有的CVB模型、Cai模型、WLZL模型、Li模型和Jin模型相比，实验结果表明本文模型能够得到更准确的分割结果。然而本文的模型仅考虑了图像的两相分割，对于多相分割适用性不强。因此，在后续的研究中，将基于本文模型，对多相分割做进一步研究。