电磁感应双杆问题加速度的一般性讨论
吴晓松
(重庆涪陵第五中学校 重庆 408000)
1 问题的提出
双杆问题作为电磁感应中一个常见的物理模型[1],涉及到电磁感应、安培力、牛顿运动定律和动量定理、动量守恒定律及能量守恒定律等,一直是教师在教学过程中不能回避的问题.在各种教学参考资料中经常能见到有关这种模型问题的讨论,尤其是双杆最终加速度的问题对于学生来说受力分析仍是一大难点.平时我们遇到的练习题中常常是导轨光滑,宽度一定,磁感强度处处分布均匀,且不受到外力的情况.比如下面这个题.
【例1】如图1所示,两根足够长的固定的平行金属导轨位于同一水平面内,两导轨间的距离为L.导轨上面横放着两根导体棒ab和cd,构成矩形回路,如图所示.
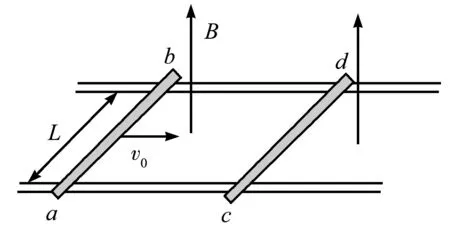
图1 例1题图
原题解析:ab棒向cd棒运动时,两棒和导轨构成的回路面积变小,磁通量发生变化,于是产生感应电流.ab棒受到与运动方向相反的安培力作用做减速运动,cd棒则在安培力作用下做加速运动.在ab棒的速度大于cd棒的速度时,回路总有感应电流,ab棒继续减速,cd棒继续加速.两棒速度达到相同后,回路面积保持不变,磁通量不变化,不产生感应电流,最终两棒以相同的速度v做匀速运动.两棒加速度都为零,但是在稳定状态之前,两棒是有加速度的.
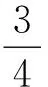
(1)
此时回路中的感应电动势和感应电流分别为
(2)
(3)
此时cd棒所受的安培力
F=IBL
(4)
所以cd棒的加速度为
(5)
由以上各式,可得
(6)
做完该题后,班上一学生向老师问道,如果两棒长度不等,导轨不光滑,情况又如何呢? 确实解完该题后都留给教师和学生一种意犹未尽的感觉,因此笔者在教学之余将这一模型一般化后(两杆不等长,导轨粗糙,磁场分布不同且受到外力)进行了再讨论.
2 模型的建立及求解
【例2】如图2所示[2],有一足够长的水平放置的平行金属导轨间距为l1,其间有匀强磁场,磁感应强度为B1;与之相连的有间距为l2的足够长的水平放置的平行金属导轨,导轨间有匀强磁场,磁感应强度为B2.将长为l1,质量为m1,电阻为R1的金属棒b放置在离连接处足够远的位置,金属棒b与导轨的摩擦因数为μ1;将长为l2,质量为m2,电阻为R2的金属棒a放置在离连接处足够远的另一位置,金属棒a与导轨的摩擦因数为μ2.导轨与金属棒a,b构成闭合回路,其中导轨的电阻可忽略不计.当恒力F垂直作用在金属棒b上,水平拉动金属棒.求两金属棒最终的加速度之比.
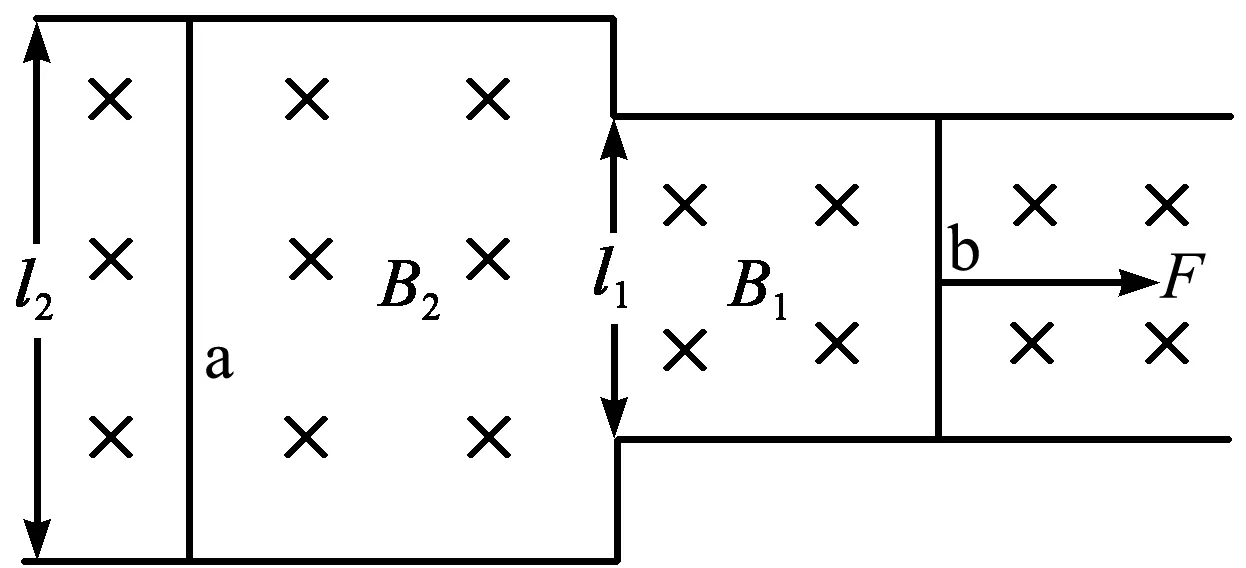
图2 例2题图
解:研究b棒
(7)
研究a棒
(8)
研究闭合回路
(9)
由式(7)、(8)、(9)可得
(10)
令
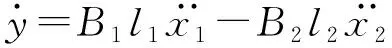
所以式(10)简化为
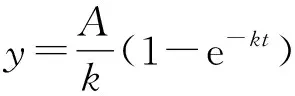
(11)
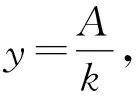
(12)
由式(12)可以看出I与R1,R2无关,即经过足够长时间后电流为一定值.下面计算经过足够长时间后两金属棒各自的加速度及其比值,有
(13)
(14)
通分后
即
(15)
可见两金属棒的加速度各自趋于一个稳定值,且
3 对加速度比值的再分析
通过上面的求解结果可知,在恒定拉力作用下两金属棒最终加速度的比值与摩擦因数和电阻都没有关系,只与各自的磁感强度和宽度有关,无疑这是一个非常简洁而美妙的结果.实际上这个结果的确具有合理性,对两金属棒来说水平方向受到不为零的合力时,系统必然具有加速度而且最终达到稳定状态时(比如匀加速)电流I必须恒定或者说电流的变化率为零.因为
所以
或者
特别地,若B1=B2,则
若l1=l2,则
中学物理资料上常常是其中的一根导体棒受恒定的外力且
l1=l2B1=B2
这就得到我们所熟悉的结论
如果两杆都不受到外力,最终稳定后两杆的加速度均为零,这就是原题的情景.当然如果其中一根杆受到恒定的外力,最终稳定后两杆的加速度之比就是一个简洁的结果

