基于MATLAB可视化程序处理经典物理复杂问题的教学研究*
董少光
(佛山科学技术学院物理与光电工程学院 广东 佛山 528000)
1 引言
经典物理是高等院校物理类专业非常重要也是非常难学的专业基础课.在日常的经典物理教学过程中,学生普遍反映该课程中的某些物理概念离现实生活非常遥远,理解起来也非常抽象、枯燥和晦涩难懂,还有些物理概念和物理规律学生难以灵活掌握以及很难理解其具体的实际运用.很多学生在学习经典物理时感到心理压力很大,教师在教学过程中也感到非常棘手和茫然.因此,对经典物理课程的课堂教学模式进行相应的改革和探索更好的教学方式具有非常现实的指导意义.
在以往的经典物理课堂教学过程中,教师特别注重培养学生严格、严密、严谨的科学素质,要求学生拥有扎实的物理基础理论知识功底[1].但是,在目前的经典物理教学过程中往往存在以下3个突出的问题:一是学生所学的经典物理主要是以复杂的高等数学知识推导的物理基础理论知识为主,而学生往往由于高等数学知识掌握得不够扎实或不够熟练,导致学习或理解复杂物理问题的效果不理想;二是在经典物理的教学过程中,学生不太容易听得懂比较抽象复杂的物理问题,或者课堂上似乎听得懂,但课后作业却很难独自揣摩明白并准确求解;三是学生不太能理解经典物理教学内容中某些难度较大的物理概念或物理规律背后所隐含的物理意义,不太容易将这些物理概念和物理规律与生活中对应的实际问题结合起来进行研究分析[2].
2 MATLAB可视化程序在经典物理中的优势
在经典物理的课堂教学过程中,教师普遍认为学生对经典物理问题中含有一些复杂的高等数学公式不能自如地处理是学习物理概念和掌握物理规律时感到困难的主要原因[3].如果教师能恰当地使用MATLAB软件的可视化程序,就可以将很多用复杂高等数学公式表达的物理公式转变为直观形象的二维、三维视图或动态仿真图.学生对某些复杂经典物理问题的理解就可以由抽象的理性思维转变为容易接受的感性思维.这样的教学方式可以大大减轻学生在学习经典物理过程中面对繁琐复杂的高等数学公式产生的心理障碍或心理压力,可以很好地提高学生对复杂经典物理问题的深入领悟和物理意义的透彻理解.当然也就较好地提高了学生学习经典物理的兴趣和积极性,提高了教师讲授经典物理的课堂教学质量以及教学效果等等.
MATLAB是一款面向科学计算、数据可视化以及交互式程序设计的工程软件,具有强大的数据计算功能,简单易学易懂,编程效率高,在工程计算和数值分析领域有着十分广泛的应用[4].如果在经典物理的课堂教学过程中应用MATLAB软件的可视化程序进行辅助教学,适当地使用MATLAB软件中可视化程序绘出二维或三维视图,制作可视化的动态模拟仿真图像,就可以将抽象复杂的经典物理问题具体化、形象化、可视化乃至模拟仿真化,再结合经典物理中的某些物理理论对这些复杂经典物理问题进行深入的分析,就可以很好地降低学生在学习经典物理过程中遇到复杂问题时的恐惧心理,就能够提升学生对经典物理课程内容中某些晦涩难懂的物理理论的感性认识,并更好地分析物理现象产生的本质和原因,进一步激发学生对经典物理的学习兴趣.更重要的是通过经典物理这门专业基础课程的学习,可以很好地培养学生良好的创新意识和科学素质,提高学生的动手操作能力和创新实践能力[5].
3 MATLAB可视化程序在经典物理中的应用
经典物理是学生最早利用高等数学知识解决实际生活问题的专业基础课,涉及的知识面非常广,主要包括力学、热学、声学、光学、电磁学、原子物理等多个学科[6].在经典物理的课堂教学过程中,根据经典物理课程的特点,教师特别注重培养学生处理复杂物理问题的能力、动手实践操作的能力、科学计算模拟的能力、科学分析概括的能力等等[7].教师在经典物理的课堂教学过程中,对复杂的物理教学内容适当地应用MATLAB软件的可视化程序进行动态模拟仿真,让学生在不需要在实验室做实物实验的情况下,就可以直观地观察到某些特殊的物理现象或物理变化过程,让学生体会到学习经典物理课程并非真的是枯燥乏味的,反而是非常生动有趣和容易理解接受的.
为了使学生能够很好地掌握抽象的、难以理解的经典物理复杂问题的物理概念和物理规律,在经典物理的教学过程中,教师利用MATLAB软件的可视化程序将这些物理概念和物理规律用直观生动的动态仿真图像表示出来.MATLAB的可视化程序是基于数组和有关特定函数,运行相关程序得到的视图,该视图是对物理概念和物理规律的定量描述,而不是普通意义的示意图[8].因此可以定量地分析物理概念和物理规律中所涉及的各个因素对某个物理量产生的各种影响,这种教学模式是传统的教学模式根本不可能做到的.
在经典物理的教学过程中,刚性小球在地面上连续弹跳问题是学生难以理解的质点运动学问题.利用MATLAB软件的可视化程序对刚性小球的运动过程进行动态仿真模拟,就能直观显示刚性小球弹跳的水平距离与反弹系数、速率比这两个参数之间的变化关系,从而更容易理解刚性小球在弹跳运动过程中所隐含的物理运动规律.
【例1】一个刚性小球以水平速度v0从高为h处抛出,与地面发生碰撞后继续向前跳跃.假设小球在水平方向没有受到摩擦,在竖直方向碰撞后的速率与碰撞前的速率之比为k(k<1),k称为反弹系数.求小球到静止时运动的时间和水平距离.小球的水平速率与第一次反弹的速率之比为一常数,对于不同的反弹系数,小球的运动轨迹有什么特征?
解析:小球与地面碰撞后做斜抛运动,在水平方向是匀速直线运动,在竖直方向是上抛运动,小球每次与地面碰撞后的速率为
vi=kiv0
(1)
小球第i次做斜抛运动的方程为
xi=xi0+vixti
(2)
(3)
其中ti是小球第i次斜抛运动的时间,xi0是小球第i次斜抛运动的水平初始位置.
小球第i次做斜抛运动的时间为
(4)
小球弹跳的总时间为
(5)
反弹系数决定小球弹跳的总时间.
小球弹跳的水平总距离为
(6)
算法:取平抛高度h为距离单位,取平抛时间T0为时间单位,取v0为速度单位,则小球做平抛运动的无量纲方程为
(7)
(8)
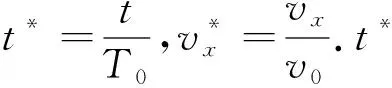
小球第i次做斜抛运动的无量纲方程为
(9)
(10)
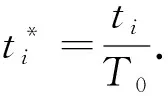
(11)
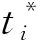
(12)
小球弹跳的水平距离可表示为
(13)
小球弹跳的水平总距离由反弹系数和速率比决定,反弹系数和速率比是可调节参数.
MATLAB可视化程序如下所示:
%平抛小球在地面上跳跃的轨迹的主程序
clear
%清除变量
vx=0.1;
%速率比
k=0.9;
%反弹系数
fun(vx,k)
%调用函数文件画轨迹
fun(vx,0.8)
%调用函数文件画轨迹
%平抛小球在地面上跳跃的轨迹的函数文件
function fun(vx,k)
if k>=1 return,end
%如果速率比
大于1则返回
tm=(1+k)/(1-k);
%运动时间
xm=2*vx*tm;
%最远的距离
figure
%创建图形窗口
plot([0,xm],[0,0],′LineWidth′,3)
%画
地平线
grid on
%加网格
axis equal
%使坐标间隔相等
axis([0,xm,0,1])
%坐标范围
fs=16;
%字体大小
title(′平抛小球在地面上跳跃的轨迹′,′FontSize′,fs)
%标题
xlabel(′水平距离itx/h′,′FontSize′,fs)
%横坐标标签
ylabel(′竖直高度ity/h′,′FontSize′,fs)
%纵坐标标签
txt=[′速率比itv_x/v m_0:′,num2str (vx)];
%水平速率与平抛落地速率比文本
txt=[txt ′,反弹系数:′,num2str(k)];
%反弹系数文本
text(0,0.5,txt,′FontSize′,fs)
%显示
速率比文本
txt=[′itT m=′,num2str((1+k)/(1-k)),′(2ith/g m)^{1/2}′];
%运动时间字符串
txt=[txt ′,itX m=′,num2str(xm),′ith′];
%连接运动距离
text(xm/4,0.8,txt,′FontSize′,fs)
%显示
运动时间
dt=0.001;
%时间间隔
tm=1;
%平抛时间
t=0:dt:tm;
%平抛的时间向量
x=2*vx*t;
%平抛的横坐标
y=1-t.^2;
%平抛的纵坐标
i=0;
%斜抛次数清零
hold on
%保持图像
while tm>0.01
%斜抛时间较大则循环
comet(x,y)
%画彗星式轨迹
plot(x,y,′LineWidth′,2)
%补画轨迹
i=i+1;
%斜抛次数
tm=2*k.^i;
%斜抛运动时间
t=0:0.001:tm;
%时间向量
x=x(end)+2*vx*t;
%横坐标
y=2*k^i*t-t.^2;
%纵坐标
end
%结束循环
当小球水平速率与平抛落地速率之比取0.1,反弹系数取0.9时,小球的运动时间为19T0,水平运动的总距离为3.8h,运动轨迹如图1所示.
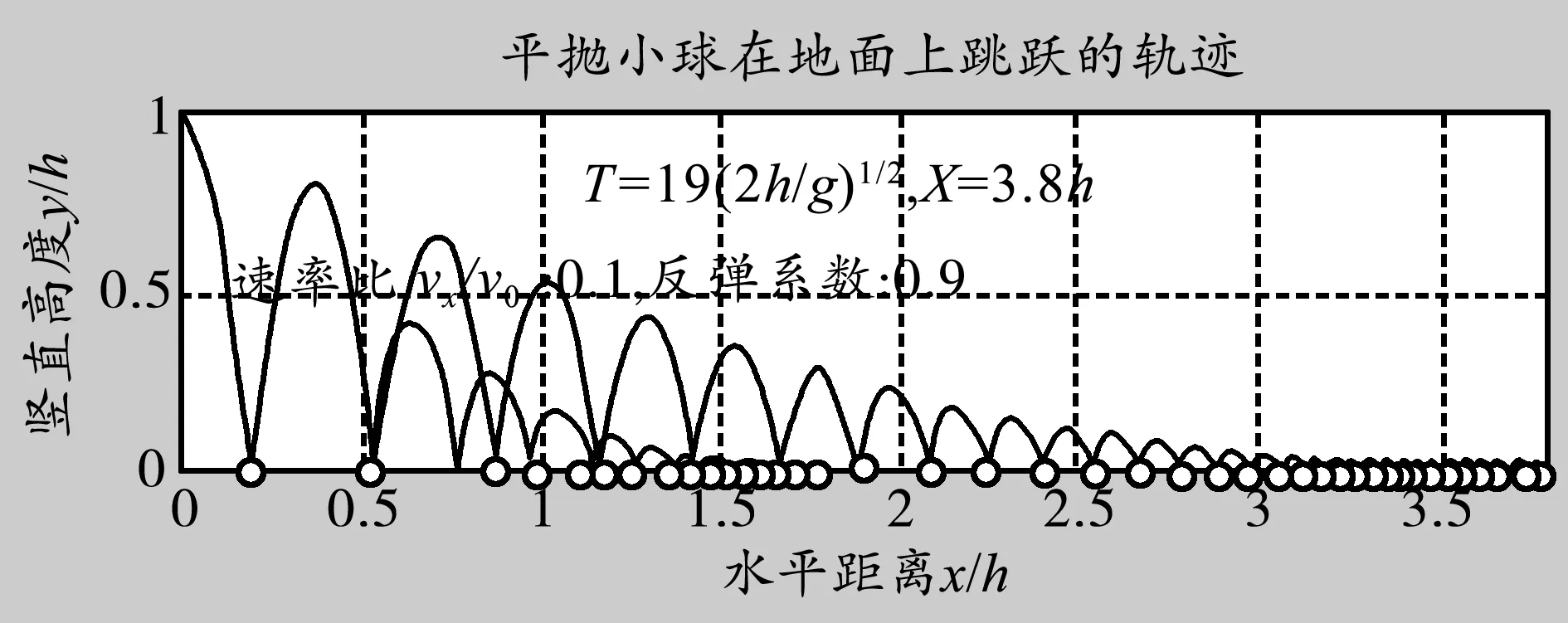
图1 平抛小球在反弹系数为0.9的运动轨迹
当小球水平速率与平抛落地速率之比仍取0.1,但反弹系数取0.8时,小球的运动时间为9T0,水平运动的总距离为1.8h,运动轨迹如图2所示.
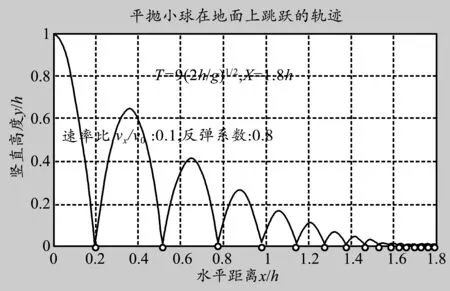
图2 平抛小球在反弹系数为0.8的运动轨迹
这样我们就可以得出,在水平速率与平抛落地速率之比一定时,反弹系数越小,小球运动时间越短,水平运动的总距离也越短.在反弹系数一定时,小球运动时间不变,水平速率与平抛落地速率之比越大,水平运动的总距离也越长.从图中可直观看到小球的运动轨迹及小球弹跳水平总距离,物理过程非常清晰和直观,学生也非常容易理解物理过程.
在经典物理的教学过程中,均匀链条从光滑桌面上下落的问题也是学生难以理解的质点动力学问题之一.通过利用MATLAB软件可视化程序对均匀链条在下落过程中下落部分的运动过程进行动态模拟仿真绘图,就能直观地显示均匀链条下落部分的位移和速度变化规律,从而更容易理解和接受均匀链条在下落过程中的物理运动规律.
【例2】一链条长为l,放在光滑的桌面上,其中长为b的一段处于下垂状态,如图3所示.链条从静止开始运动,求链条的运动规律,并求链条滑出桌面的时间和速度各为多少?
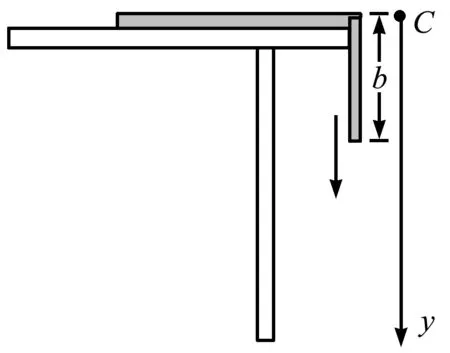
图3 链条下落的示意图
解析:由牛顿第二定律和牛顿第三定律以及数学的微积分和初始条件可以求得,链条下落的时间与高度的关系为
(14)
链条下落长度(高度)的规律为
(15)
当链条完全滑出桌面时,所需要的时间为
(16)
链条的速度为
(17)
对以上的解析式进行约化处理,令
取约化时间
再取约化长度
约化速度
其中
则链条的长度和速度分别为
y*=b*cosht*v*=b*sinht*
(18)
当链条全部滑出桌面时所需要的时间可表示为
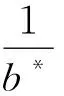
(19)
链条全部滑出桌面时对应的速度可表示为
(20)
取初始下垂的长度b为参数向量,取时间t为自变量向量,形成矩阵来计算链条下滑的长度和速度,用矩阵画线法画出链条长度和速度的曲线族,作出的图像如图4和图5所示.
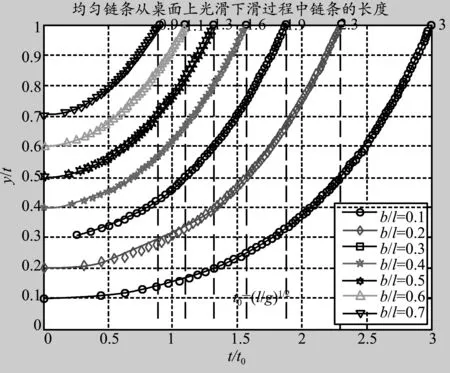
图4 均匀链条下落过程中离开桌面长度的变化规律
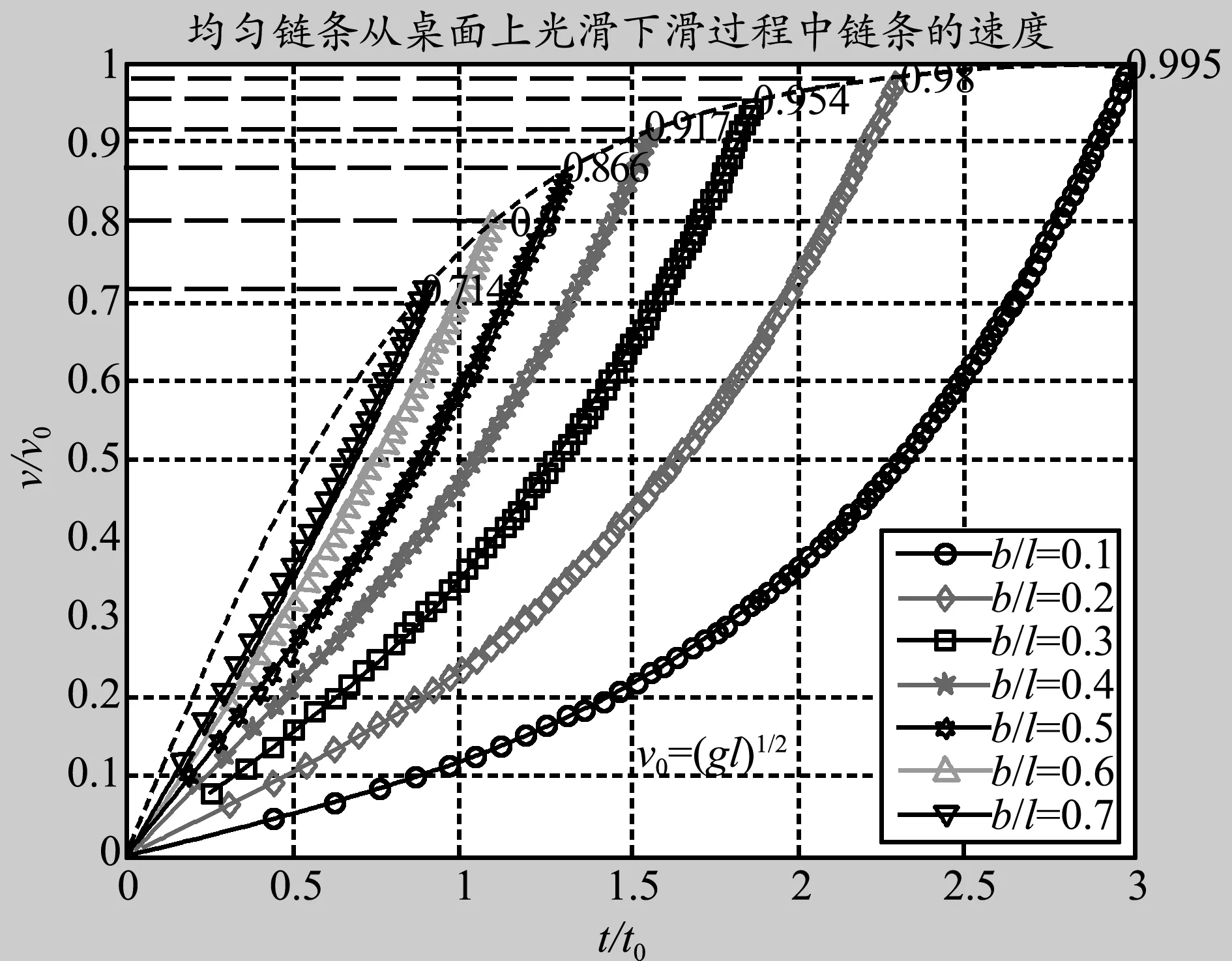
图5 均匀链条下落过程中下落速度的变化规律
MATLAB可视化程序如下所示:
% 均匀链条从光滑桌面上滑下来的运动规律曲线
clear
%清除变量
b=0.1:0.1:0.7;
%b与l的比值向量
y=0:0.01:1;
%链条滑过的长度y
与l的比值向量
[B,Y]=meshgrid(b,y);
%化为矩阵
Y(Y %使不符合条件的 元素为非数 T=acosh(Y./B); %求时间 %T(imag(T)~=0)=nan; %将复数 改为非数 V=B.*sinh(T); %求速度 V=sqrt(Y.^2-B.^2); %求速度(同上) figure %创建图形窗口 plot(T,Y,′LineWidth′,2) %画长度曲线族 plot(T(:,1),Y(:,1),′o-′,T(:,2),Y(:,2),′d-′,T(:,3),Y(:,3),′s-′,... T(:,4),Y(:,4),′p-′,T(:,5),Y(:,5),′h-′,T(:,6),Y(:,6),′^-′,...T(:,7),Y(:,7),′v-′) %画长度曲线族 fs=16; %字体大小 xlabel(′itt/t
m_0′,′FontSize′,fs) %时 间比标签 ylabel(′ity/l′,′FontSize′,fs) %长度比标签 title(′均匀链条从桌面上无摩擦滑下的长度′,′FontSize′,fs) %加标题 grid on %加网格 n=length(b); %比值个数 legend([repmat(′itb/l
m=′,n,1),num2str(b′)],4) %加图例 text(1.5,0.1,′itt
m_0=(itl/g
m)^{1/2}′,′FontSize′,fs) %加时间单位文本 tm=max(T); %求运动时间 text(tm,ones(size(tm)),num2str(tm′,2),′FontSize′,fs) %标记时间 axis tight %帖轴 hold on %保持图像 stem(tm,ones(size(tm)),′--′) %画杆图 figure %创建图形窗口 plot(T,V,′LineWidth′,2) %画速度曲线 plot(T(:,1),V(:,1),′o-′,T(:,2),V(:,2),′d-′,T(:,3),V(:,3),′s-′,... T(:,4),V(:,4),′p-′,T(:,5),V(:,5),′h-′,T(:,6),V(:,6),′^-′,... T(:,7),V(:,7),′v-′) %画速度曲线族 xlabel(′itt/t
m_0′,′FontSize′,fs) %时间 比标签 ylabel(′itv/v
m_0′,′FontSize′,fs) %速 度比标签 title(′均匀链条从桌面上无摩擦滑下的速度′,′FontSize′,fs) %加标题 legend([repmat(′itb/l
m=′,n,1),num2str(b′)],4) %加图例 grid on %加网格 text(1.5,0.1,′itv
m_0=(itgl
m)^{1/2}′,′FontSize′,fs) %速度单位文本 vm=max(V); %求最终速度 text(tm,vm,num2str(vm′,3),′FontSize′,fs) %标记最终速度 hold on %保持图像 plot([zeros(size(tm));tm],[vm;vm],′--′,′LineWidth′,2) %画水平线 b=0.1:0.01:1; %b与l的比值向量 tm=acosh(1./b); %全部滑下的时间 vm=sqrt(1-b.^2); %全部滑下的速度 plot(tm,vm,′--′,′LineWidth′,2) %画全部滑下的速度和时间曲线 在经典物理的教学过程中,利用MATLAB软件的数值模拟可视化可以使学生理解物理概念和物理规律变得轻松.例如利用MATLAB软件的可视化程序可以使经典物理中的刚性小球弹跳问题和均匀链条下滑过程的位移和速度变化问题变得生动、直观、形象.利用MATLAB软件的可视化程序可以将涉及的物理规律的模拟结果以动态变化图形的方式呈现.从这些可视化的动态图形中,学生很容易理解物理规律以及物理量之间的变化趋势,更好地理解该物理规律产生的原因或条件.利用MATLAB软件的可视化程序可以使经典物理的教学在一定的程度上减轻了教师课堂教学难度,同时也降低了复杂的高等数学计算过程对学生理解物理概念和物理规律的干扰.这种辅助教学手段如果利用得当的话,一定可以提高教师经典物理的课堂教学效果,激发教师的教学激情,更重要的是激发学生学习经典物理的积极性和兴趣,快速提升学生的科学理论素质和科学领悟能力.4 结论

