核心素养视野下初中数学解题元认知训练的实践
付敏


【摘要】培养学生的解题能力,是数学教学的核心目标.由备战中考的课堂解题教学常常陷入两难的境地得出,元认知训练在解题教学中的重要作用和逻辑必然性.大量学者通过对元认知训练在解题教学中的探索和实践,丰富了对元认知的理性和感性认识.
【关键词】数学解题;元认知训练;实践;认识
【基金项目】本文系江西省教育科学“十三五”规划2019年度课题“核心素养视野下初中数学元认知训练实践研究”(编号:19PTYB004)的研究成果之一.
一、问题提出
近几年江西省中考数学题难度较稳定,其热点和难点多活跃于在数学核心素养中拓展抽象型知识结构下的高阶思维活动水平.一线教师对此非常关注,在总复习阶段做出部署,加强训练,然而效果却不像期待中的那样,常常处于纠结的两难境地:这些热点和难点在近几年中考中的得分率那么低,讲了吧,没多大收获,不讲吧,又觉得可惜……还是讲吧,可是怎么讲才好呢?这样的囧况如何破解?解题教学该何去何从?
二、问题分析
这种现象是解题教学的痛点,既有教法问题也有学法问题,与长期解题训练导致的学生内部对话与外部对话缺失有很大关系,最深层次的原因是:深度学习不够,学生较少关注自己在学习中的认知过程, 缺少反思和对学习策略的提炼,思考还停留在肤浅的境地,没有将知识、方法、策略纳入并加工到认知结构体系中,从而无法驾驭问题的变化和延伸.
很显然,简单问题的解决有基本模式和步骤,只需介入很少的认知元素,进行模仿就能解决;而解决没有现成解法的问题,必须深入思考,即在问题表征、联想、策略选择、计划制定、调整和監控、反思和迁移等方面都需运用认知元素和策略,认知一直贯串于高难度问题的过程中,不可缺少,思维层级越高,对认知水平的要求也就越高.如果认知得到开发重视,学生的认知水平提高,隐性认知就会向显性转化, 学生就能充分发挥自己的潜能,在解题过程中灵活多变.而如果学生的认知水平较低,其自我效能感就会骤降,学习压力也会陡然增大.
特别需要指出的是,在学习过程中发挥重要作用的认知,即元认知,而元认知水平是可以通过训练提高的.“研究表明我们可以把这些策略教给学生,包括预测结果的能力、向自己解释以改进理解的能力、记录理解上失败方面的能力.比如,交互式教学……”“元认知也指反思自己表现的能力……如果儿童对自己的学习能力缺乏洞察,几乎不能期望他们制定计划或做出有效的自我调节……”可见,利用元认知训练促进学生解决问题能力的提高显然具有可行性,而且是逻辑的必然.
三、探索与行动
依据元认知思想和内涵,我们开展了“核心素养视野下解题元认知训练”实践研究,以中考复习专题课“点位置不确定多解填空题”为例开展教学,探索解题元认知训练的方法和途径.
1.训练主题:唤醒自己,让解题成为学习进步的脚印.
2.学情分析和教学意义:
“点位置不确定多解填空题”是近几年江西省中考数学试题的热点和难点,对学生思维和运算的综合能力要求较高.通过对大量学生的试卷和作业的分析发现,少数人能真正完全掌握,多数人还存在分析不全面、思路不清、方法不灵活等亟待提高的问题.因此本文设计和安排了此课,希望唤醒学生的内在智慧,提高其数学自主学习能力.
3.教学目标:
(1)以确定点位置为目的,教会学生辨析主动点和从动点,探索动点路径,运用逻辑叠加确定符合题意的点的位置,培养学生从静态和动态两个角度分析点位置的解题意识,让学生经历丰富的探究过程,发展学生的逻辑推理和直观想象核心素养.
(2)留足够时间提问、思考、回顾、总结,发展学生元认知能力.
(3)让学生认清自己的学习层级,产生正向的自我效能感,培养实事求是的科学态度.
4.教学重点:点位置的确定和坐标求解.
5.教学难点:解题元认知的内化、迁移和运用.
6.教学特色:
本节课以发展解题能力为明线,启迪元认知为暗线,通过具有启发性的动手操作活动和导入语、交互式提问、精准分析、学习卡的运用,以及几何画板演示等教学手段,使个体获得多方位、多层次及丰富的认知体验,对发展元认知起到了很好的促进作用.
7.教学过程:
【创设情境】
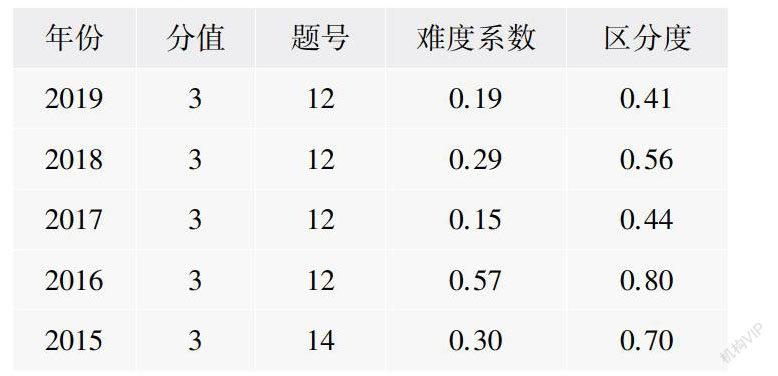
教学活动一:中考数据展示和分析
(简介:屏幕展示近5年江西省中考数学试题中多解填空题相关数据,观察后,教师分析说明:多解填空题近5年来稳定在填空题最后一题,综合性比较强,难度往往较大,有较强的区分度,有江西中考“小压轴题”“前段压轴题”之称.)
教学活动二:激发学习兴趣和学习热情
(简介:制造疑点,激发学生的好奇心和好胜心,教师问:“那怎样才能做出来呢?”然后拿出事先精心准备的、处理得有些夸张的学习卡片给学生看,鼓励道:“当然是努力啦,努力很重要,不过,方法比努力更重要,方法在这,是哪张呢?认真听课,你们就知道了,加油吧.”)
【评析】制造疑点,激发学生的好奇心和求知欲,明确学习目标、学习任务,启迪元认知知识.
【审题训练】
教学活动一:多媒体屏幕显示题目,学生完成第一次读题.
教学活动二:屏蔽题目的关键部分,学生完成第二次读题.
(简介:屏蔽的内容是“将边OA沿OD折叠,点A的对应点为A′,若点A′到矩形较长两对边的距离之比为1∶3”,屏蔽后,提问学生回答完整或再提问学生补充完整,也可以事先准备好一张矩形纸,折叠提示.)
教学活动三:师生交流解题想法.
(简介:采用交互式提问,如:同学们打算怎么做?先做什么?再做什么?你们觉得哪里会遇到困难?这道题可能会用到哪些学过的知识?大家有什么要问老师的吗?)

