第二价格密封拍卖下建设用地指标抵扣规则研究
白月 孟卫东 黄波


考虑建设用地指标和建设用地的互补性特征,构建互补品序贯拍卖模型。考虑指标价款抵扣,通过第二价格密封拍卖模型,得到影响卖方期望收益的关键因素。并以卖方收益最大化原则得到最优折扣额度。研究发现:价格抵扣影响卖方期望收益,当建设用地指标和建设用地之间互补性较弱时,卖方期望收益随抵扣额度的增加先增加后减少;反之,当两者互补性较强时卖方期望收益随抵扣额度的增加而逐渐减少。
一、引言
在我国,工业化和城镇化的高速发展使农村人口快速向城镇转移,城镇建设用地急剧增加,但城镇建设用地指标却严重短缺。现行土地制度下,宅基地、农村集体建设用地等农村建设用地只能在本集体经济组织内部流通,既妨碍其流通而使其大量闲置,导致资源浪费;又降低其流通价格而损害农民利益。为有效解决以上问题,重庆市成立农村土地交易所,开展建设用地指标的交易试验。
鉴于此,本文以建设用地指标和建设用地为研究对象,针对现行城乡建设用地指标定价机制实施的现状及存在的问题,研究互补品序贯拍卖下建设用地指标抵扣机制,提高稀缺土地资源的配置效率。
建设用地指标交易中,成渝两地均未开放建设用地指标交易二级市场。若指标权利人2年内未能成功拍得建设用地,即建设用地指标未能成功落地,土交所将以原价收回建设用地指标。孙芬等指出,当前地票交易仅限于一级市场,对城乡之间资金、技术、土地等要素流动的促进作用还较为有限,故建议在明确市场功能定位、完善市场调节和监管机制的基础上,逐步开放地票交易二级市场。张泽梅阐述了两地地票成本的差别。目前对于建设用地指标的定价的研究涉及不多,将互补品序贯拍卖应用于建设用地指标交易的研究有一定研究意义。
二、模型
在这一背景下,本文将互补品序贯拍卖模型应用于建设用地指标和建设用地交易。应用第二价格密封拍卖,将拍卖分为两个阶段,分别拍卖建设用地指标和建设用地。考虑不同抵扣额度下,在互补品两阶段序贯拍卖中卖方的期望收益,以期得到使卖方期望收益最大化的最优的抵扣额度。
风险中性的卖方通过连续两场拍卖分别出售指标和建设用地,每阶段的赢者支付该阶段的次高竞价,n个具有独立私人价值的风险中性的竞拍者参加拍卖(n≥3)。所有竞拍者在指标中均不知道建设用地对自已的价值,但赢得指标使得建设用地对竞拍者的价值增加为原价值的r倍,其中r≥1,在每场拍卖结束之后,卖方公布拍卖结果。卖方拍卖前承诺:如果指标拍卖阶段的赢者在建设用地拍卖中同样胜出的话该赢者将会得到一定的指标价款抵扣d,其中0≤d≤1。
以下信息为完全信息:
1.竞拍者i的估值(v1i,v2i)满足:v1i,v2i独立地服从[0,1]上的均匀分布,(i∈{3,4,5,…,n}下同)
2.若竞拍者i只赢得指标,则指标与建设用地对的i价值分别为v1i,v2i;若競拍者i同时赢得指标和建设用地,则两件物品对i的价值为其中v1i+rv2i,其中r为协同因子。
(一)卖方的期望收益
任意正的指标价款抵扣都将导致卖方收益的增加。然而卖方事前并不清楚竞拍者的估价,仅仅知道他们随机地分布在[0,1]区间上。若卖方作为理性的卖方选择最大化自己事前期望收益的指标价款抵扣额度,则
命题1 卖方所选取的最优的指标价款抵扣应满足:
d*∈argmax{maxE(d)} (1)
其中
且若n≥3,则则竞拍者i获得物品的情况、条件及支付如表1
命题1是一个非线性规划问题,其最优解与n有关。即卖方所选取的最优指标价款抵扣额度与参加拍卖的人数有关。显然,卖方并非给予越多的指标价款抵扣就可以得到越高的收益。分析该规划问题得
命题2的证明 由式(1)(2)可知,命题2的最优解仅与n有关。
1.存在性。
命题2说明合适的指标价款抵扣可以增加卖方的期望收益,最优的指标价款抵扣随着参加拍卖的人数增加而减小,可以算出d*(5)≈0.2472,d*(20)≈0.05。当参加拍卖的竞拍者足够多时,没有必要再采取指标价款抵扣。这也说明在实际拍卖活动中当参加拍卖的竞拍者较少时,卖方者需要给予较多的指标价款抵扣额度以刺激竞拍者之间的竞争。
命题3最优价款抵扣额度下的卖方的事前期望收益E(d*(n))为协同因子r的增函数。
(二)命题3的证明
命题3说明最优价款抵扣下的卖方者期望收益随着建设用地指标和建设用地之间互补性的增强而增加。
三、算例
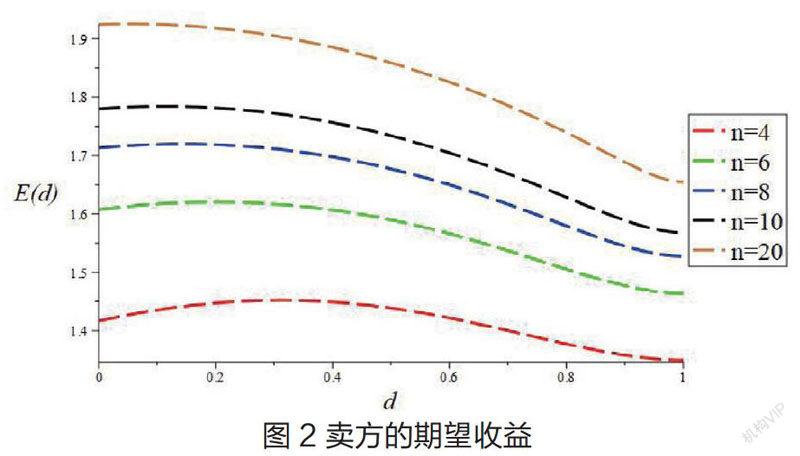
在具有指标价款抵扣的建设用地指标和建设用地互补品序贯二价拍卖中,考虑卖方的期望收益。取协同系数r=1.25(如图1)、r=1.5(如图2),以抵扣额度d为横轴,分别绘制n=4、n=5、n=8、n=10、n=20时E(d)的图形。
由图1、图2可知,在两阶段互补品序贯拍卖过程中,当竞标人数取值较小时,以n=4为例,卖方的期望收益随着指标价款抵扣额度d的增加先增加后减小,但变化幅度不大。当竞标人数取值较小时,以n=20为例,卖方的期望收益随着指标价款抵扣额度d的增加逐渐减小,且减小较为明显。竞拍人数n较小时,竞拍参与人数的增加使卖方的期望收益明显增大。竞拍人数n较大时,竞拍参与人数的增加对卖方的期望收益影响较小。对比图1、图2可知,协同系数由r=1.25增加为r=1.5,卖方的期望收益随之增大。由此可知,卖方若想获得最大的期望收益,必然要找到与之对应的最优的指标价款抵扣额度,这一最优抵扣额度仅与竞拍参与人数n有关,这印证了命题3。同时,在指标抵扣额度相同的情况下提高竞拍者参与建设用地指标交易的积极性,增加竞拍参与人数也可以提高卖方期望收益。
四、结语
在考虑卖方给予开发商建设用地指标价款抵扣的前提下,针对建设用地指标和建设用地具有互补性的特征,将互补品的序贯二价拍卖模型应用于建设用地指标和建设用地两阶段拍卖。本文有以下结论:
价格抵扣影响卖方期望收益,当建设用地指标和建设用地之间互补性较弱时,卖方期望收益随抵扣价款的增加先增加后减少;反之,当两者互补性较强时,卖方期望收益随抵扣额度的增加而逐渐减少。最优的指标抵扣额度下,卖方期望收益随着建设用地和建设用地指标之间互补性的增强而增加。
(作者单位:重庆大学经济与工商管理学院)

