基于滑模控制的能馈型交流电子负载的研究

张 鑫， 廖冬初，2， 蔡华锋,2， 周 浩

(1 湖北工业大学 电气与电子工程学院， 湖北 武汉 430068；2 湖北工业大学 太阳能高效利用湖北省协同创新中心， 湖北 武汉 430068)

由于传统电源出厂测试使用的模拟负载存在巨大能源消耗的问题，将测试能量回馈到待测电源输入端的交流电子负载具有能耗低、体积小、易调节等优点。目前，直流能量回馈型交流电子负载采用两级电路，前级是负载模拟单元，采用三相电压型PWM(脉冲宽度调制)整流电路，后级是能量回馈单元，采用移相全桥电路[1]。经典的PID(比例-积分-微分)控制在三相电压型PWM整流电路中已经得到了广泛的应用[2]。但是三相电压型PWM整流器是一个多输入多输出的强耦合非线性系统，传统的PID控制方法应用到三相电压型PWM整流电路中，仍存在鲁棒性差、难以满足输入电流快速响应指令的要求等[3]。

滑模变结构控制诞生于20世纪50年代，它对系统模型要求不高，而且还具有系统响应速度快、抗干扰能力强以及实现简单等诸多优点[4]。目前，国内外针对滑模控制抖振问题的研究很多，其中典型的是准滑模方法、高阶滑模方法、动态滑模方法和趋近律方法[5]。双幂次趋近律是一种改进的幂次趋近律，提高了系统状态趋近滑模面的速度[6]。积分滑模面能够减小稳态误差，同时控制律中不会出现状态变量的二阶导数，实现起来比较简单[7]。

采用传统的双闭环控制策略在负载变化及电压波动时，直流母线电压波动较大，响应速度慢，稳态性能差[8]。为了改善三相VSR(电压整流器)的性能，负载模拟单元采用直接电流控制，能量回馈单元采用双环控制，因篇幅有限，本文主要对负载模拟单元展开研究。

1 负载模拟单元的数学模型

三相电压型PWM整流器(VSR)主电路如图1所示。ea、eb、ec、ua、ub、uc分别为三相电网相电压和三相VSR交流侧相电压；ia、ib、ic为三相VSR交流侧相电流；L、R分别为交流侧单相滤波电感和单相输入线路等效电阻；C为母线电容；RL为母线电容的放电电阻。

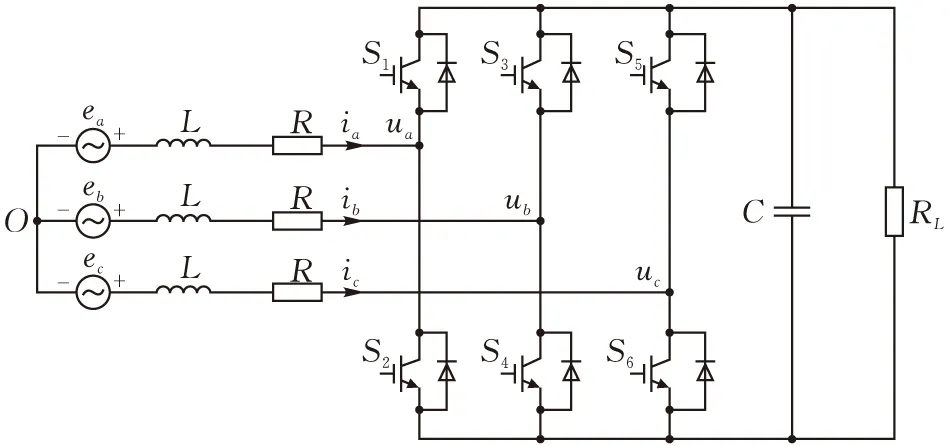
图 1 三相VSR主电路结构图

三相电压型整流器在两相同步旋转坐标系下的数学模型为：

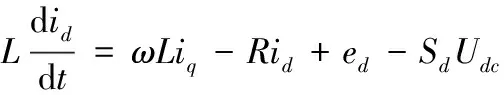
(1)

式中:id和iq分别为相电流ia、ib、ic在dq坐标系下的交流侧电流；ed和eq分别为相电压ea、eb、ec在dq坐标系下的交流侧电压；Sd和Sq分别为开关函数在dq坐标系下的变量；ω为三相电网相电压角频率。式(1)表明三相电压型PWM整流器是一个多输入多输出的强耦合非线性系统，故无法采用一般的线性化控制技术实现精确解耦控制。

2 滑模控制器设计

系统在滑模变结构控制器作用下，可以沿设定的状态轨迹进行滑模运动，且不受系统被控对象的参数及外界扰动的影响，在滑模变结构控制下系统具有良好的鲁棒性。在四种经典的趋近律中，指数趋近律是趋近效果比较好的一种趋近律，指数趋近律的趋近速度随着与滑模切换面距离的变化而变化。

2.1 一般指数趋近律控制器

一般指数趋近律：

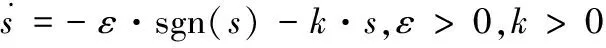
(2)

式中:ε，k都是大于零的常数，ε表示切换函数的幅值，k表示指数趋近项系数。

从式(2)可知，一般指数趋近律由两项组成，当系统远离滑模切换面时，误差变量e相对较大，此时等速趋近项和指数趋近项共同作用收敛于滑模面，k越大，系统响应速度越快，系统抖振越大；当系统靠近滑模切换面时，误差变量e相对较小，指数趋近项-k·s相对较小，等速趋近项-ε·sgn(s)发挥主导作用，ε越小，系统趋近速度越慢，系统抖振越小。因此，一般指数趋近律无法同时满足系统响应速度和抖振的控制要求。

2.2 改进型指数趋近律控制器

为了减弱经典趋近律控制器所带来的抖振问题，同时保证系统的响应速度，在经典指数趋近律基础上进行改进，得出的指数趋近律如下：

(3)

上式中的变速趋近项ε·s2·sgn(s)起到了关键作用，趋近速度大小与s2成正比。当系统状态点离滑模面比较远时，趋近速度比较大；随着控制器对系统误差的调节，系统状态点离滑模面越来越近，趋近速度也越来越小。此时系统逐渐趋于平衡，系统在滑模面上的抖动也将是经典趋近律的抖动的平方次。所以，采用了变速趋近项代替一般指数趋近律中的等速趋近项，不但能增加系统跟随给定的快速性，而且能减弱滑模切换面上的抖振问题。

观察式(3)，引起系统在滑模面上抖振的主要原因是由于开关函数sgn(s)的正负切换特性，因此，为了进一步减弱抖振问题，本文提出双曲正切函数tanh(a·s)来代替sgn(s)，因此本文的指数趋近律改进为

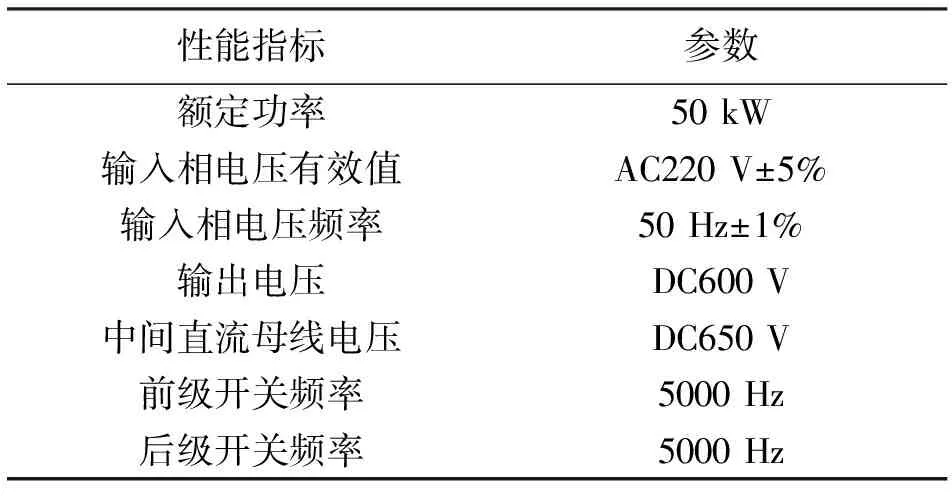
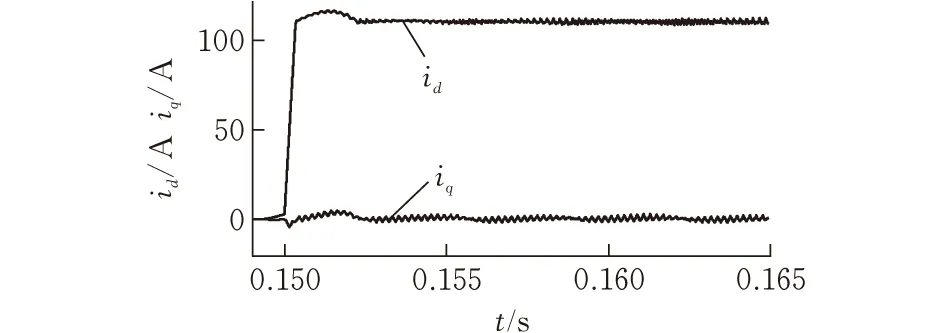
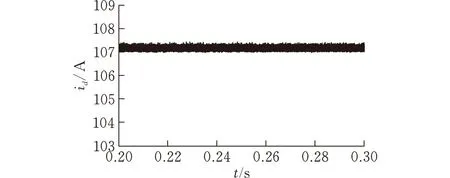
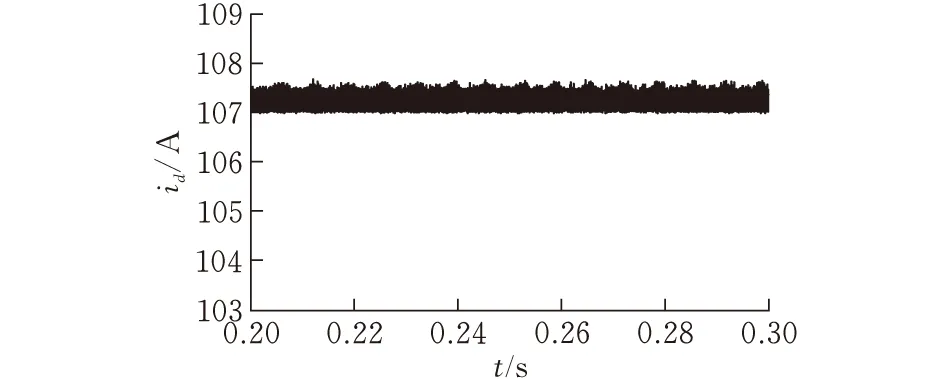
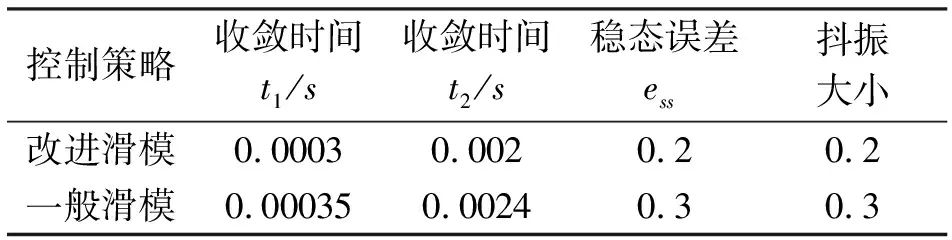
图2给出不同a值下的tanh(a·s)变化曲线，可以看出当s>3或s<-3时，tanh(a·s)≈sgn(s)；当-3

图 2 tan h(a·s)变化曲线

(4)

2.3 滑模面的设计

滑模面的选择直接关系到滑动控制过程的稳定性、存在性、可达性以及良好动态性能等问题。传统线性滑模面控制在系统跟踪过程中会存在一定的稳态误差，而积分滑模面在传统线性滑模面基础上增加了积分项，在跟踪过程中不存在稳态误差且具有良好的动态性能。以两相静止坐标系的d轴为例，选取积分滑模面s为：

(5)

选取李雅普诺夫函数为：

(6)

对式(6)两端求导，可得：

(7)

根据式(4)趋近律结合式(5)滑模面和式(1)被控对象数学模型可得系统在两相静止坐标系d轴上的滑模控制器输出为：

系统在两相静止坐标系q轴上的滑模控制器输出为：

3 仿真验证

为验证滑模控制对于三相VSR负载输入电流具有较好的跟踪性能和抗干扰能力，在Matlab中进行仿真，根据以上设计搭建模型，负载模拟单元仿真参数：交流侧电感2 m H，线路等效电阻0.01Ω，输入预充电电阻2Ω，直流母线电容8000 uF。能量回馈单元仿真参数：谐振电感10 uH，隔直电容72 uF，高频变压器1:1.5，滤波电感800 uH，滤波电容54 uF，输出预充电电阻20Ω。交流电子负载主要技术指标见表1。

表1 交流电子负载主要技术指标

在额定功率下，输入电流有功电流给定值为107 A，无功电流给定值为0。以输入单相电压和电流为例分析，输入单相电压峰值为311 V，输入侧单相电压和电流波形见图3。

(a)改进型指数

(b)一般指数图 3 两种控制策略下的输入单相电压和电流波形

在两种控制策略下，输入单相电流峰值均能达到107 A，并且输入电流与输入电压相位相同，频率一致，输入电流实现跟踪控制，交流电子负载在额定功率运行。

对输入电流进行坐标变换，得到输入电流的d轴分量Id和q轴分量Iq(图4)。由图4a可知，收敛时间分别为t1=0.0003和t2=0.002。由图4b可知，收敛时间分别为t1=0.00035和t2=0.0024。可以看出，在改进型指数趋近律控制下，系统的收敛速度加快了12%，因此在趋近律中引入s2项可加快系统收敛速度。

(a)改进型指数

(b)一般指数图 4 两种控制策略下的输入电流收敛过程

以输入电流d轴分量Id的稳定运行波形为例，分析双曲正切函数对输入电流的抖振现象具有减弱作用(图5)。系统以额定功率运行，输入电流的d轴分量Id给定值为107A。由图5a可知，输入电流的d轴分量Id稳态值为107.2 A，稳态误差为0.2 A，抖振幅值为0.2 A。由图5b可知，输入电流d轴分量Id稳态值为107.3 A，稳态误差为0.3 A，抖振幅值为0.3 A。

(a)改进型指数

(b)一般指数图 5 两种控制策略的输入电流抖振波形

可以看出，采用双曲正切函数，输入电流的稳态误差较小，抖振幅值也较小，对系统稳态性能具有较好的优化效果。结合图4和图5输入电流波形，具体性能指标对比见表2。由表2可知，采用双曲正切函数替换开关函数，对输入电流的抖振具有明显减弱效果，从而提高输入侧的功率因数及抑制输入电流高频谐波，减少对交流电网的谐波污染。采用变指数趋近项替换一般指数趋近项，加快了系统收敛速度，使系统更快趋于稳定。

表2 两种控制策略性能指标对比

4 结论

为提高交流电子负载的跟踪性能和稳态性能，对于负载模拟单元，提出了改进型指数趋近律的直接电流控制策略。通过仿真验证，和一般指数趋近律控制相比较，采用改进型指数趋近律的滑模变结构控制可进一步减弱抖振问题，减小稳态误差，并且加快系统收敛速度，因此在趋近律中引入s2项和双曲正切函数具有较好的控制效果。不过收敛速度和抖振幅值等系统指标有待进一步提升。