基于随机波动率模型的沪深300ETF期权定价
郁瑞澜, 商 豪
(湖北工业大学理学院, 湖北 武汉 430068)
2019年12月23日,沪深300ETF期权在上海证券交易所上市。沪深300ETF期权是继上证50ETF期权之后我国上市的第二只ETF期权。它是以华泰柏瑞沪深300ETF为标的的欧式期权,在提高市场稳定性和流动性、完善金融市场等方面有重要意义。因此,沪深300ETF期权定价的合理性至关重要。1973年,Black和Schole[1]通过大量数据分析发现金融衍生品和标的资产的价格服从含有漂移项的布朗运动。利用无套利理论将欧式期权的价格表示成股票价格与时间的微分方程,得到欧式看涨期权价格的解析解。因B-S模型常数波动率、常数利率等假设条件过于理想化,无法处理资产价格带跳、发放红利对其影响等问题,国内外学者不断对其进行改进以适应实际情况。在真实金融市场中,波动率微笑[2]、波动率聚集[3]等现象非常常见,因此学者们以随机波动率为重点,改进了一系列新的期权定价模型。1993年,Heston[4]提出连续时间波动率的平方根模型,并经过大量实证发现Heston模型比B-S模型的定价结果更精准。在实证分析中,马尔科夫链蒙特卡罗方法(MCMC)实现了抽样分布随模拟进行而改变的动态模拟过程,它既不需要事先估计参数,也无需对大量数据进行拟合优化。Jacquier E等(1994)[5]最先将MCMC法引入随机波动率模型的参数估计中。Jacquier E发现MCMC法的参数估计精度最高。Nilsson(2016)[6]针对随机波动率模型的参数估计进行了大规模的模拟研究,发现不同样本量下对不同参数进行估计时均是MCMC法的误差最小。张瑶(2020)[7]针对沪深300ETF期权波动率的随机性提出AHBS模型、Heston模型,并用最小二乘法进行参数估计。刘莹等(2019)[8]用粒子群(PSO)智能算法改善了Heston模型对香港恒生指数期权进行定价时的参数校准问题。Azencott R , Ren P[9]根据Heston模型参数的矩估计建立了选择时间间隔和收益率数据二次采样频率的标准。本文基于Black-Scholes期权定价模型和随机波动率模型对沪深300ETF期权的定价问题展开实证研究。
1 模型基础
1.1 Black-Scholes期权定价模型
假设某一资产的价格是S(t),由经典Black-Scholes公式(下称B-S公式)可知,在一个连续时间上面,资产价格的波动率方程为:
其中,W(t)表示标准Wiener过程,σ为波动率(σ>0),μ是漂移项。在经典B-S公式中,波动率σ和漂移项μ是与时间无关的非随机变量。尽管根据这个公式可以求出波动率的公式解,但是 “波动率与时间无关”的假设显然不符合实际情况,所以求得的波动率模型与实际波动率相差很大。
1.2 Heston随机波动率期权定价模型
随机波动率模型(Stochastic Volatility Model)的主要思想是在假设标的资产价格服从维纳过程的基础上,将波动率视为一个随机过程。Heston模型是SV模型的一种,它假设资产价格的波动率服从均值回复平方根过程,也就是CIR(Cox-Ingersoll-Ross)过程。在中性风险下,Heston模型的形式:
其中,Ws(t),Wσ(t)是维纳过程,它们的相关系数记为ρ。模型的参数为μ,α,β,σ0,ρ,μ有时也取为无风险利率r。
为了便于参数估计,将式写成:

1.3 马尔科夫蒙特卡洛方法
假设θ是一个多维的参数向量,现希望从分布P(θ|X)中产生一列随机值。首先,将θ分为几个几个部分,即θ=(θ(1),θ(2),θ(3),…,θ(n)),其中P(θ(1)∣θ(2),θ(3),…,θ(n),X),P(θ(2)∣θ(1),θ(3),…,θ(n),X),…,P(θ(n)∣θ(1),θ(2),…,θ(n-1),X)能够简单地得到它的随机抽样值,也称为全条件后验分布。
Gibbs算法具体的抽样过程为:
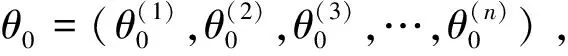

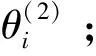
⋮
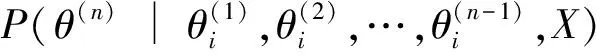
最终得到抽样值θ1,θ2,θ3,…,θN,为了消除初始值θ0的影响,舍去前面M个值。
设f(θ)是我们感兴趣的函数,令

1.4 Heston模型的贝叶斯估计后验密度
Heston模型的离散形式为:
其中,ΔWi(tn)=Wi(tn+1)-Wi(tn),i=1,2。
记
Y=(y1,…,yn)T,Δ=(Δ1,…,Δn)T
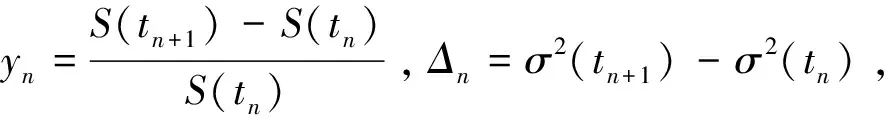
Zn~N(μn,Σn)
其中
由此,可以得到给定参数(Y,Δ)的条件分布为

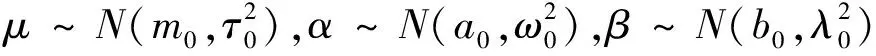
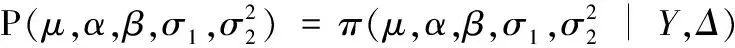
由此,接下来可以计算出Gibbs抽样所需要的条件密度:
其中
m1=
其中
其中
其中,
2 实证分析
2.1 数据的选择与描述性分析
根据在值程度,期权可分为虚值期权、实值期权和平值期权。本文选取2019年12月23日至2020年8月31日到期日在两个月内的9只在值程度不同的沪300ETF看涨期权的日交易数据,以日期为y轴,隐含波动率为z轴作出隐含波动率的曲面图(图1)。
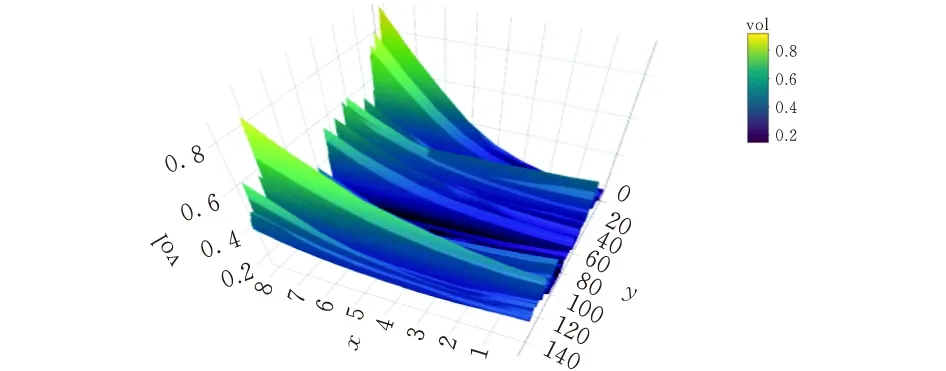
图 1 样本期权波动率曲面图
由图1可见,隐含波动率与在值程度的关系呈现较为明显的“波动率微笑”曲线。相对实值期权和虚值期权来说,平值期权的波动率处于低点,也较为稳定。由此可见,沪300ETF期权的隐含波动率不是一个常数,说明B-S公式中“波动率为常数”的假设与现实情况不符。
本文仅选取2019年12月23日至2020年8月31日到期日在两个月内的沪300ETF平值看涨期权的日交易数据用以实证分析,理由如下:第一,平值期权的隐含波动率较稳定;第二,平值期权的交易较活跃,在交易量较大的情况下,交易价格更贴近其价值;第三,平值期权的Vega值比较高,期权价格对标的资产价格的波动率敏感,更能体现不同定价模型之间的差异。
本文无风险利率使用1个月Shibor利率(即“上海银行业同业拆借利率”),数据来自东方财富网,由爬虫获得,其余数据均由WIND金融终端导出。
2.2 参数估计结果
常见的MCMC法有Metropolis-Hastings(M-H)算法和Gibbs算法。M-H算法有两个缺点:一是在高维情况下由于接受率的原因导致算法收敛时间长,二是有些高维数据特征的联合分布很难求出来。在M-H算法基础上发展而来的Gibbs算法将参数分为几个部分,每个部分的抽样都基于其他参数的前一个抽样值,最终可以收敛于真实的后验值,很好地克服了M-H算法的缺点。鉴于MCMC法的优点以及Gibbs算法在高维特征时的优势,本文采用MCMC法中的Gibbs算法对Heston模型的参数进行估计,结果如表1所示。

表1 参数估计结果
2.3 实证结果与误差分析
以日期为x轴,价格为y轴,分别画出B-S公式、Heston模型和期权实际价格的折线图(图2)。
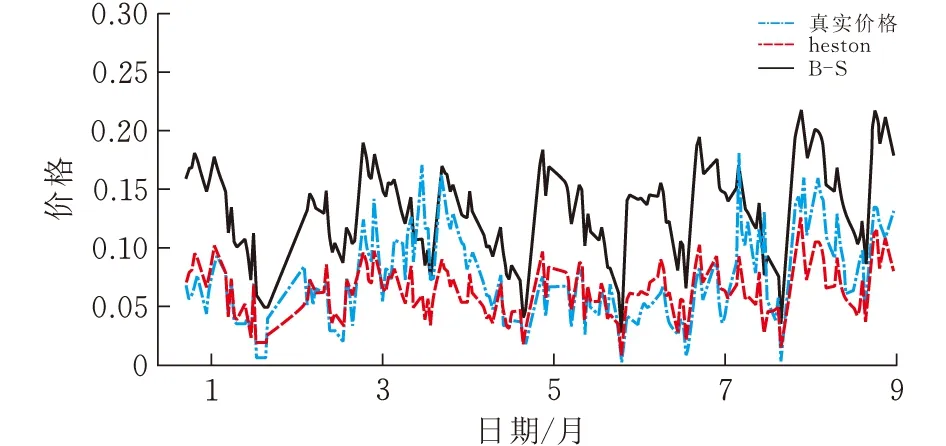
图 2 B-S公式、Heston模型和期权实际价格的折线图
如图2所示,B-S模型的价格波动幅度比Heston模型大,这是由于Heston模型假设资产价格的波动率服从均值回复平方根过程,所以价格波动幅度相对平稳。此外,整体上看,B-S的定价结果偏高,Heston模型比B-S模型的定价结果更贴合实际,但是当标的资产价格大幅波动时,B-S定价结果比Heston定价更准确。
记理论价格为yn',期权实际价格为yn,样本总量为N,用平均绝对误差
平均相对误差
平均绝对相对误差
均方误差
分别计算B-S公式和Heston模型的误差。
MAE和MAPE主要用于衡量定价误差的大小;MAPE指明了误差的方向,即表明了理论价格比实际价格低还是高;MSE强调数据变化程度,MSE越小模型数据越精准。由表2可以看到,在四种误差衡量方法之下,Heston模型都比B-S公式表现得更好。
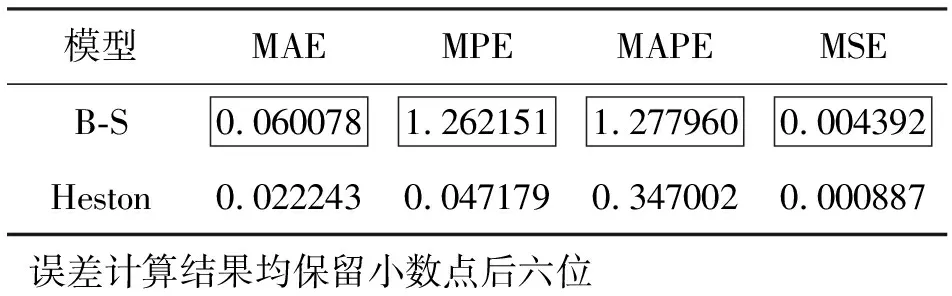
表2 不同模型的定价误差PHam

