基于广义Sigmoid函数的车辆紧急转向避障策略研究

郭晓宇 王芃 陈宁 徐晓美 姚嘉凌

（南京林业大学，南京 210018）

主题词：紧急转向避障 Mittag-Leffler函数 Sigmoid函数 改进Stanley算法

1 前言

车辆遇到紧急工况时，可采用紧急制动或紧急转向的方式避开障碍物[1]。当前自动紧急制动（Autonomous Emergency Braking，AEB）技术日趋成熟，而自动紧急转向（Autonomous Emergency Steering，AES）作为下一代主动安全技术正在迅速发展中。AES 技术根据无人车感知模块提供的道路信息生成避障路路径，避障路径规划方法分为数学公式描述法、人工势场法和随机树搜索法等。徐媛[2]采用Sigmoid 函数初步规划避障路径，使用模型预测控制对路径进行再规划。赵志国等[3]提出了基于Sigmoid 函数曲线以及物理约束的避障路径规划方法，建立考虑最优曲率预瞄与闭环反馈的驾驶员模型对规划出的路径进行跟踪。白成盼等[4]使用Sigmoid 函数作为智能车的换道轨迹，基于微分平坦理论构造非线性性能函数进行优化求解，完成速度规划，但避障的情况比换道更为复杂，所以Sigmoid 函数作为避障曲线具有局限性。闫尧等[5]采用五次多项式作为换道轨迹，约束车辆横向速度、横向加速度和横摆角速度，采用序列二次规划算法求解参数。边明远等[6]建立了安全车距模型，采用正弦加速度模型规划避障曲线，能够保证车辆行驶的横向稳定性，缩短了紧急避障的极限距离。人工势场法[7]广泛应用于路径规划，其假设物体在运动中受到力场作用，原理简单、实时性强，但存在着局部最小值问题，且参数需要长时间标定。杜明博等[8]提出了连续曲率（Continuous-Curvature RRT，CC-RRT）算法，可在复杂工况下规划出避障路径，但限于低速工况下。在路径跟踪算法方面，斯坦利（Stanley）跟踪算法[9]不同于纯跟踪算法精度依赖于预瞄距离，该算法主要考虑车辆动力学和瞬时车速的影响。靳欣宇[10]等在Stanley 预瞄转向几何模型的基础上，设计出优化函数选择最优预瞄时间，但优化函数的系数选择过程复杂。Amer 等[11-12]提出一种取消预瞄距离的改进Stanley 跟踪器，增加横摆角速度误差作为反馈量，但进行高速路径跟踪时存在抖动。

本文考虑车辆避障时的约束条件和安全性，提出基于广义Sigmoid 曲线作为避障路径，并考虑到Stanley 算法对前方曲率与车速的变化不敏感，在高速跟踪时存在抖动的问题，提出一种增加横摆角速度阻尼项的Stanley跟踪器。最后，通过仿真验证所提出策略的有效性。

2 基于广义Sigmoid函数的紧急避障路径设计

2.1 米塔-列夫勒函数

米塔-列夫勒（Mittag-Leffler）函数[13]是指数函数的直接推广。本文引入2个参数的Mittag-Leffler函数：

其中，Γ函数由以下无穷积分定义：

双参数Mittag-Leffler函数的特例为：

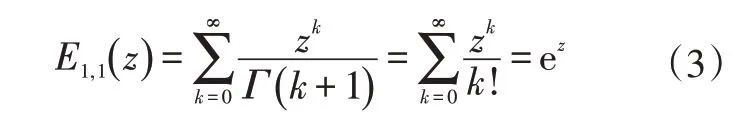
式中，z为变量；α、β为可变参数。

2.2 广义Sigmoid避障函数的提出

Sigmoid函数用数学公式可描述为：

式中，ε、c、k为形状参数。

由图1 可知：曲线的最大斜率为kε∕4，k、ε越大，转向越剧烈；从初始位置转向到最大斜率的距离c越小，单位时间内转向幅度越大；避障路径的横向目标位移k根据具体避障情况决定。

图1 Sigmoid曲线参数含义

引入Mittag-Leffler广义Sigmoid避障函数：

由于车辆存在运动学约束，要求参考路径连续、横摆角连续、曲率连续有界，生成的避障函数必须连续且一阶和二阶导数连续[14]。Mittag-Leffler 函数和指数函数一样具有无限可导的性质，广义Sigmoid 避障函数满足以上作为路径的要求。由式（5）可知，广义Sigmoid表达式较Sigmoid函数增加2个可调参数。

2.3 新增参数对曲线特性的影响

其余参数不变，α、β变化时曲线的图像变化情况如图2所示。相较于Sigmoid函数，广义Sigmoid函数的α、β在给定范围内变化时，初始、终止位置变化小，后半段形状改变程度较前半段大。广义Sigmoid的一阶导数和二阶导数分别如图3、图4所示。β增大会使避障曲线的最大航向角和最大曲率增大，同时曲线的末位置航向角变为负值。α增大，避障曲线的最大航向角和最大曲率均减小，且末位置航向角变为正值。α、β改变对车辆进行紧急避障有实际意义，相比Sigmoid 曲线多用于换道工况，广义Sigmoid曲线根据末位姿限制生成避障曲线。

图3 广义Sigmoid函数航向角变化情况

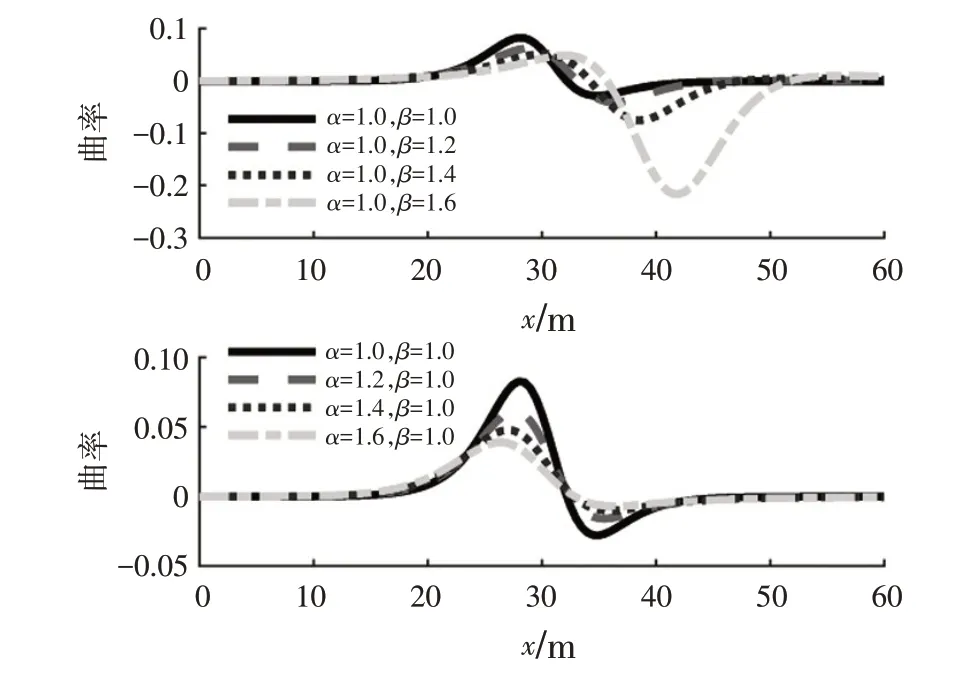
图4 广义Sigmoid函数曲率变化情况

3 实时最优避障路径生成和路径跟踪

3.1 三自由度车辆模型

如图5 所示，引入侧倾建立包括侧向、侧倾和横摆角的三自由度车辆模型，同时考虑弹簧影响[15]，建立三自由度车辆动力学方程：

图5 三自由度车辆模型

式中，mv为车辆总质量；v为车辆速度；θ为车辆质心侧偏角；r为横摆角速度；ms为簧上质量；hs为质心高度；p为簧上质量侧倾角速度；Jzz为汽车横摆惯性矩；Jxx为簧上质量绕侧倾轴转动的侧倾惯性矩；Jxz为簧上质量对侧倾和横摆2个方向组成的平面的惯性矩；Y、M、L分别为车体重心处的侧偏力、横摆力矩和侧倾力矩。

设Yf、Yr分别为前、后车轮的侧偏力，考虑到轮胎侧偏特性和几何特性，有：式中，Cf、Cr分别为前、后轮轮胎侧偏刚度；df、dr分别为汽车重心至前、后轴的距离；δf、δr分别为前、后轮转角；Rf、Rr分别为车体侧倾运动影响系数；ϕ为簧上质量侧倾角。

可得车辆的侧偏力矩和横摆力矩为：

对于侧倾运动，可认为侧倾角较小，因此，sinϕ≈ϕ，cosϕ≈1，于是有：

式中，Cϕ、Kϕ分别为总侧倾阻尼和总侧倾刚度；g为重力加速度。

整车的运动方程为：

式中，φ为车辆横摆角。

3.2 最优路径代价函数

3.2.1 车辆转向安全性

车辆的侧向加速度ay和轨迹的曲率κ近似满足，其中vx为车辆横向速度，在紧急转向避障工况下车辆的纵向加速度为0，车辆的加速度约束为：

式中，ax为横向加速度；μ为路面附着系数。

3.2.2 路径安全性加权项

将障碍物简化为圆形，考虑路径在满足车辆安全距离约束的情况下，与障碍物的碰撞区域没有重合，需满足：

式中，(xob,yob)为障碍物位置；R为障碍物半径；d为安全距离。

碰撞检测不能完全反映路径的安全性，路径跟踪的精度不高或检测障碍物的位置误差过大时，路径与障碍物接近将导致碰撞发生。

如图6 所示，只考虑避开障碍物问题，候选曲线①的安全性高于候选曲线②。评估路径的特点在于靠近障碍物的一段路径对整个路径的安全性影响最大。

图6 碰撞检查

考虑车辆避障时的安全性与实时性，使用高斯卷积和碰撞风险的方法评估路径的安全性：

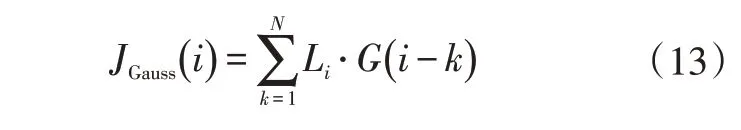
其中：

式中，JGauss(i)为曲线簇中的碰撞安全代价加权项；Li为第i条候选路径的碰撞检测结果；G(j)为高斯卷积函数；N为候选路径i离散点数量；Δρ为比例因子；σ为标准差。

3.2.3 目标位姿约束加权项

车辆的位姿为(xt,yt,θt)，应尽量趋近于设定路径的末位置(x(tend),y(tend))和末位置航向角，且满足末位置约束Jp和末位置航向角偏离约束Jt：

3.2.4 归一化处理

考虑到各加权项具有不同的数量级，导致选取比例因子困难，所以将各加权项的权值进行均值归一化处理：

式中，J为加权项；Jmax、Jmin分别为加权项的最大、最小值。

构建评价曲线的代价函数：

式中，w1、w2、w3为比例因子；分别为归一化后JGauss、Jp、Jt的值。

3.3 改进Stanley路径跟踪器

Stanley算法中控制参数间的几何关系如图7所示。

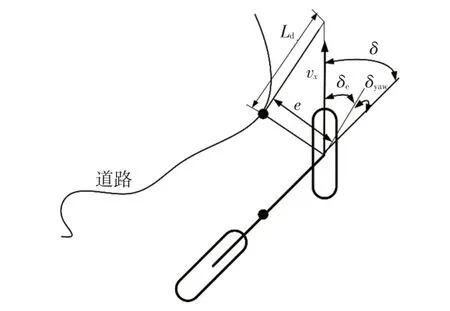
图7 Stanley算法原理

设δyaw(t)为车辆航向角与参考轨迹航向角的误差，e(t)为横向误差。预瞄距离Ld与车辆纵向速度vx成比例：

式中，kp为比例系数。

车辆前轮转角关系可以表示为：

为了提高算法在高速转向时的跟踪精度和车辆的稳定性，对Stanley算法进行改进。取消预瞄距离，使用横摆角速度误差作为反馈量提供未来轨迹预测。设Ksofe为平缓系数，当车速较低时，减小横向偏差对前轮转角变化的影响，当车速较高时几乎不影响控制。此时整个轨迹跟踪器成为比例反馈控制系统，同时，为了减小系统的超调量和延迟时间，增加横摆角速度阻尼作为微分反馈调节项kd(rdiscrete(i)-rdiscrete(i+1))。其中rdiscrete(i)为离散时间内横摆角速度，i为前一控制周期的索引值。整个Stanley算法改写为：

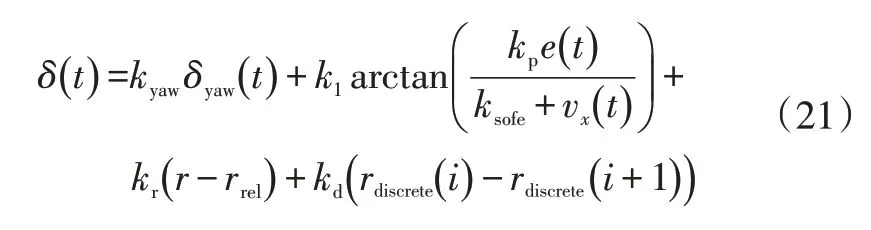
式中，kyaw、k1、kr、kd为比例系数；rref为参考横摆角速度。

3.4 仿真评价与分析

3.4.1 搭建仿真环境

为验证紧急避障算法的可行性，开展仿真验证，采用改进Stanley跟踪器对车辆进行跟踪，车辆以20 m∕s的速度沿规划好的路径行驶，探测到障碍物时，车辆执行紧急避障。三自由度车辆参数如表1所示。

表1 三自由度车辆部分参数

3.4.2 仿真结果分析

3.4.2.1 路径安全性加权项

如图8 所示，道路边界和障碍物均进行碰撞检测，如图9所示，在生成的避障曲线簇中曲线6的碰撞安全值最小。路径安全性加权项对靠近避障曲线的障碍物和道路边界更加敏感。

图8 碰撞检测示意

图9 候选路径碰撞风险

若不存在道路的约束，则曲线1 为最安全的避障曲线。由图2 可知，此时α最大，增大α能够提高避障曲线的安全性。曲线11 为β最大的曲线，增大β会降低安全性。

3.4.2.2 代价函数分析

图10所示为根据代价函数生成的车辆坐标系下目标点为(60 m,3.5 m)，目标航向角分别为1°、0°、-1°的最优化避障曲线。生成的目标路径对应目标航向角为1.2°、0.09°、-0.55°，末位置点与目标点的误差分别为0.110 0 m、0.000 3m、0.010 0 m，表明设计的代价函数能够满足避障需求，相比由于一般Sigmoid曲线，可设置避障末位姿，用于更多避障工况。

图10 代价函数生成的路径示意

3.4.2.3 改进Stanley跟踪器

图11 所示为不加阻尼项与增加阻尼项的2 种Stanley 跟踪器对传统Sigmoid 函数路径的跟踪效果，2种Stanley 跟踪器均能对一般Sigmoid 函数路径进行精确跟踪且跟踪效果类似，从图12可知，增加阻尼项的跟踪器输出的前轮转角比不加阻尼项的更加平稳，在车辆高速转向时能提高转向平稳性。由此可知，改进的Stanley跟踪器更适合高速转向时的路径跟踪。

图11 2种Stanley跟踪器跟踪传统Sigmoid路径

图12 2种Stanley跟踪器的前轮转角对比

3.4.2.4 广义Sigmoid函数路径跟踪

对改进Stanley跟踪器的各参数进行调整，图13、图14所示分别为参考路径与跟踪路径的对比结果和跟踪误差，参数调整后改进Stanley跟踪器能够精准地跟踪参考路径，最大侧向误差小于0.035 m，随着广义Sigmoid函数的α发生改变，路径后半段的转弯角度持续增大，跟踪的最大侧向误差持续减小，说明改进Stanley跟踪器能够感知路径前方的曲率变化，能够更好地对转弯路径进行跟踪。

图13 路径跟踪效果

图14 路径跟踪误差

图15 所示为路径跟踪过程中前轮转角的变化情况，车辆跟踪时，前轮转角变化的绝对值不超过1.8°，且变化平稳，说明在整个跟踪过程中车辆能够保持稳定。

图15 前轮转角变化

4 结束语

本文提出了一种基于广义Sigmoid函数的紧急避障路径，可用于紧急避障且可调整车辆末位姿，相比于一般Sigmoid函数路径，应用的避障工况范围更广，扩展了Sigmoid 函数在紧急避障中的应用场合。同时，设计的考虑车辆末位姿的代价函数能够筛选出最优避障曲线且耗时很短，符合紧急避障时快速生成路径的要求。仿真结果表明：路径安全加权项对障碍物和道路边界敏感，能够作为判断路径安全性的指标；改进Stanley跟踪器能够实现在高速紧急避障时精确跟踪路径，且减小了高速跟踪时前轮转角的抖动，使转向更加平稳；在前方道路曲率发生变化时，依然能够保持跟踪的精度且车辆能够平稳转向。