面向不完备分类型矩阵数据的集对k-modes聚类算法

张春英，高瑞艳，王佳昊，陈 松，刘凤春，任 静，冯晓泽

1(华北理工大学 理学院，河北 唐山 063210) 2(华北理工大学 迁安学院，河北 唐山 063210) 3(河北省数据科学与应用重点实验室，河北 唐山 063210)

1 引 言

聚类是一个基础研究领域，在数据分析中起着重要的作用.在原型聚类中，k-means聚类算法[1，2]对于处理大型数据集非常有效，但其仅适用于数值型数据集，并不适用于处理分类型数据集.为此，Huang提出了k-modes算法[3]，通过分类样本的简单匹配来计算两个样本之间的距离，解决了分类型数据的聚类问题.此后，学者们在更好的初始化技术或更有效的距离度量方面，对k-modes算法进行了许多改进[4-7]，但其处理的都是由一组属性特征描述的样本，而在实际数据库中，存在由多组属性特征描述的矩阵样本数据[8].例如，用户的购物记录，每个用户是一个样本，然而每个用户都会购买多个商品，而且购买的商品种类和数量也不相同，因此，就会产生分类型矩阵样本数据.传统的简单匹配计算两个样本之间距离的方式不能直接用于处理这类数据集.另外，由于数据遗漏、不完整、读取限制等现象，会导致大量缺失值存在.例如，用户的购物记录，由于数据存储过程不当和出于保护用户隐私的目的，就会存在某些记录值缺失的情况，因此，有必要研究不完备矩阵数据集的聚类问题.

传统聚类算法的结果，是用具有清晰边界的集合表示，其只能表示样本与类簇之间的两种关系，即样本在集合中则属于类簇，否则不属于，而在许多应用中，样本与类簇之间存在3种类型的关系：属于、可能属于和不属于，是因为目前所收集的信息具有局限性，对于有些样本和类簇之间的关系无法进行准确判断，则给出第3种关系：可能属于.为此，Yu在传统聚类的基础上，引入三支决策[9，10]的思想并提出了三支聚类的框架[11]，其聚类结果通过两个集合表示，分别是典型对象集合和边缘对象集合.然而，考虑样本和类簇之间3种关系的聚类算法大多是针对数值数据设计的，对分类数据的研究较少.

在分类型数据聚类的研究中，传统距离度量方法一般只能使用一个特征向量来表示具有多组属性特征描述的矩阵数据，然而这样会导致丢失大量原始信息，不能做到对所有的数据进行综合考虑.另外，通常面临的数据带有缺失值，是一种不完备矩阵数据.为了解决上述具有不完备、分类型矩阵数据集的聚类问题，同时考虑样本和类簇间的不确定关系，提出了一种面向不完备分类型矩阵数据的集对k-modes聚类算法(MD-SPKM).

1)为了解决矩阵数据集不完备、不确定性的问题，将集对信息粒[12](set pair information granule)的相关理论引入到k-modes聚类算法中，对传统k-modes算法的距离公式进行改进，提出了矩阵样本间的集对距离度量公式；

2)考虑样本和类簇间的不确定关系，给出了类内平均距离的定义，用于将肯定属于类簇的样本与可能属于类簇的样本进行区分.此外，针对样本可能与多个类簇存在关系的情况，给出了判断样本是否属于多个类簇的阈值计算公式；

3)提出了面向不完备分类型矩阵数据的集对k-modes聚类算法，形成了由正同域、边界域和负反域组成的集对聚类结果，正同域中的样本肯定属于这个类簇，边界域中的样本可能属于这个类簇，负反域中的样本不属于这个类簇；

4)与现有4种代表性算法进行实验对比分析，结果表明该算法可以有效处理不完备分类型矩阵数据集.

2 相关工作

在聚类算法中，样本间距离度量是很关键的一步，针对分类型数据，学者们提出了多种距离度量方法.比如，Huang等[13]提出的基于相互依存冗余度量的计算方法，不仅考虑了两个样本之间属性值本身的差异性，而且考虑了属性之间的相互影响；Zhou等[14]提出了一种针对k-modes聚类算法的全局关系差异度量方法，其不仅考虑了样本与所有聚类modes之间的关系，而且考虑了各种属性的差异，而不是简单的匹配.然而，这些距离度量方法针对的是只有一个特征向量表示的样本，可以得到较好的聚类结果，但是对具有多组属性特征描述的矩阵样本，在对其进行距离度量时，只能选择其中的一组特征来进行距离计算，不能做到对所有数据进行考虑.因此，Cao等提出了处理集值样本的Set-Valued k-modes算法[15]和fuzzy SV-k-modes算法[16]，为具有集值特征的两个样本之间定义了距离函数，并提出了聚类中心的集值模式表示.另外，Li等提出了一种用于分类型矩阵数据的MD fuzzy k-modes算法[17]，并给出了聚类中心的启发式更新算法.上述算法虽然解决了矩阵数据的聚类问题，然而其算法主要针对完备数据集.对于样本中存在的缺失值不能给予恰当的处理，因为缺失的属性值本身就具有不确定性，无论是将其删除或者填充，都会造成一定的误差.集对信息粒理论是对现有粒计算模型的拓展，将粒空间划分成正同粒、差异粒和负反粒，可以从多个角度对问题域的相同程度、对立程度以及不确定程度进行全面刻画.因此，本文将集对信息粒的知识引入到聚类分析中，对不完备矩阵数据集的聚类问题进行研究.

由于样本与类簇之间存在3种关系，学者们为了更好的刻画这种关系提出了多种三支聚类算法，如Wang等[18]基于数学形态学的腐蚀和膨胀提出的三支聚类框架；Zhang[19]根据三支权重和三支分配方法，将粗糙k-means(RKM)进行扩展，得到一种三支c-means聚类算法等.然而，上述算法的研究对象是数值型数据，关于分类型数据的研究较少，此外，目前还没有发现针对不完备分类型矩阵数据在样本和类簇之间不确定关系方面的研究工作，因此，本文将基于集对信息粒理论，提出一种面向不完备分类型矩阵数据的集对k-modes聚类算法，可以很好的对样本和类簇之间的关系进行表示.

3 相关理论

为了更好的度量不完备矩阵样本之间的距离，本文将集对信息粒理论引入到聚类分析中，对传统距离度量方式进行改进，涉及的相关定义如下：

3.1 不完备的矩阵样本

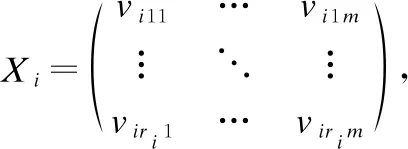
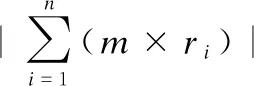
3.2 集对信息粒

集对分析[20]是以同、异、反来描述事物的一种理论.将两个事物所具有的特性作同异反分析，得出两个事物的同异反联系度表达式：ρ=a+bi+cj.a表示正同度，b表示差异度，c表示负反度，其中，i∈[-1，1]，j=-1分别称为差异度和负反度标记符号，用以识别分类信息的方向和不确定程度.

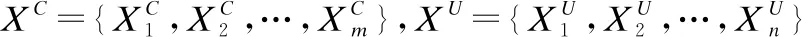
τXC：W0→[0，1]，x→τXC(x)=aR+cR

τXU：W0→[0，1]，x→τXU(x)=bR

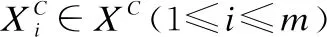
τXCs：XC→[0，1]，x→τXCs(x)=aR

τXCo：XC→[0，1]，x→τXCo(x)=cR

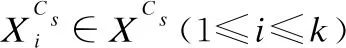
定义3[21].设n个联系数，ρ1=a1+b1i+c1j，ρ2=a2+b2i+c2j，…，ρn=an+bni+cnj，n个联系数之和仍是一个联系数：

ρ=ρ1+ρ2+…+ρn=a+bi+cj

(1)

式(1)中，a=(a1+a2+…+an)，b=(b1+b2+…+bn)，c=(c1+c2+…+cn).

3.3 传统k-modes算法

k-modes算法[3]是对k-means算法的扩展，扩展后的k-modes具有以下特征：

1)使用简单匹配的距离度量方式；

2)采用modes替代means来更新聚类中心；

3)采用频率相关策略对modes进行更新.

这些扩展排除了k-means算法中的数值限制，使得聚类能够应用到分类型数据集中.

设U={X1，X2，…，Xn}是一组分类型数据的集合，每个样本Xi={Xi1，Xi2，…，Xim}(1≤i≤n)由m个属性A1，A2，…，Am描述.集合Qj(1≤j≤k)是类簇Cj的modes，任意的Cj由ni个样本组成，其中Cj={v1，v2，…，vni}，每个类簇的Qj取每个类别属性中出现频率最高的值.

给定任意两个样本Xi和Xj，距离度量公式为：

(2)

k-modes聚类算法的目标函数为：

(3)

wij∈{0，1}，1≤j≤k，1≤i≤n；

4 集对k-modes聚类算法

4.1 矩阵样本间的集对距离度量

传统k-modes的距离度量方式只能适用于只有一组属性特征描述的样本，对于具有多组属性特征描述的矩阵型分类数据却存在一定的局限性.为了解决不完备、矩阵样本的距离度量问题，本文结合集对信息粒的相关理论，提出了基于集对联系度的距离公式，是将原本聚类过程中不同样本之间的距离扩展成包含正同度、差异度和负反度3个维度的距离定义.

定义4.(单一属性下的集对联系度)：给定矩阵样本Xi和Xj，每个样本由m个属性A1，A2，…，Am描述.将矩阵样本Xi，Xj在属性As下建立集对联系度，属性值相同的作为正同信息粒S，缺失的作为差异信息粒Q，其他的作为负反信息粒F.具体是将两样本在属性As下的记录值进行同异反分析，若对某一记录值，两样本中各有一条，则将这两条记录值都划分为正同信息粒；若存在缺失记录值，则将缺失的记录值划分为差异信息粒；将剩余的其他记录值划分为负反信息粒，则在单一属性As下建立的集对联系度公式为：

(4)

式(4)中，S的取值为相同记录值的个数，Q的取值为缺失记录值的个数，F的取值为其他记录值的个数，N的取值为两个样本属性记录值个数之和.特别注意的是当数据集是完备数据集时，不存在缺失值，则差异信息粒的个数为0.

式(4)也可以简化为：

(5)

在上述定义4中给出的是，只考虑两个矩阵样本的一组属性特征建立的集对联系度.为了能够全面考虑多组属性特征，在定义4的基础上，在定义5中给出了考虑多组属性特征的综合集对联系度的定义.

(6)

接下来，给出了一个计算两个矩阵样本X1，X2之间集对联系度的例子：

表1所示是一个矩阵样本数据集，其中X={X1，X2}，A={A1，A2，A3}，样本X1，X2之间的集对联系度计算如下：

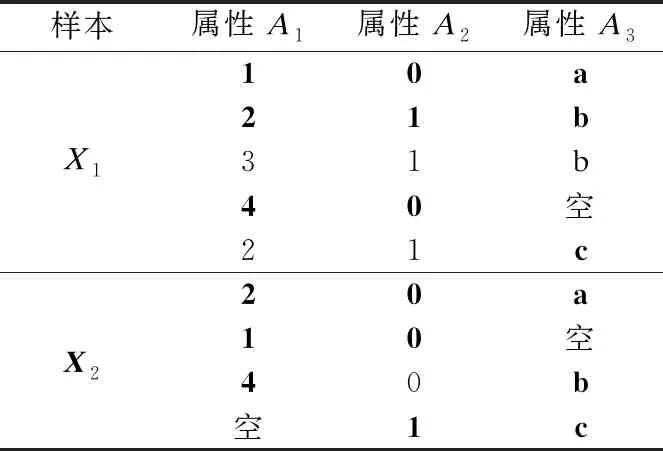
表1 矩阵样本数据集

样本X1和X2在属性A1下的集对联系度为：

样本X1和X2在属性A2下的集对联系度为：

样本X1和X2在属性A3下的集对联系度为：

样本X1和X2的综合集对联系度为：

定义6.(势函数)：对于两个矩阵样本之间建立的三元集对联系度ρ=a+bi+cj，其势函数记为：

(7)

定义7.(集对距离度量)：两个矩阵样本Xi，Xj之间建立的三元集对联系度为ρ=a+bi+cj，为了衡量两个样本之间的距离大小，并综合考虑集对联系度中的正同度、差异度和负反度，故根据集对联系度中的正同度a以及势函数Shi(ρ)来反映两个样本之间的距离大小，公式为：

d(Xi，Xj)=1/[a+Shi(ρ)]

(8)

式(8)中，a+Shi(ρ)表示两个矩阵样本之间的相似性，其中，a+Shi(ρ)的值越大，代表两矩阵样本之间的相似性越大.d(Xi，Xj)代表两矩阵样本之间的距离，其值越小表明两个样本之间距离越小.a用来衡量样本间属性值相同的程度，a越大表示两样本的相同程度越高，Shi(ρ)用来衡量两个样本之间相似性的变化趋势，Shi(ρ)的值越大表示两样本之间的相似性越大.虽然集对距离度量公式中只有正同度a和负反度c，但由于a+b+c=1，即b=1-c-a，则间接考虑了差异度b.

4.2 集对k-modes聚类结果表示

在集对信息粒空间中，定义了3种信息粒集：正同粒集、差异粒集和负反粒集.正同粒集和负反粒集属于确定信息粒，差异粒集属于不确定信息粒，其3种信息粒集正好对应聚类中存在的3种关系，因此将集对信息粒的相关理论引入到k-modes聚类中，从3种信息粒集的概念出发，提出了以正同域Cs，边界域Cu，负反域Co表示的集对聚类结果.正同域中的样本一定属于这个类簇，边界域中的样本可能属于这个类簇，负反域中的样本不属于这个类簇，这3个域具有如下性质：

(i)Cs(Ci)≠Ø

(iii)Cs(Ci)∩Cs(Cj)=Ø，i≠j

性质(i)表明每个类簇的正同域不是空集，至少有一个样本在正同域中；性质(ii)表明每个样本都必须被划分；性质(iii)表明任意两个类簇的正同域相交为空集.

4.3 算法设计思想与实现

针对不完备、分类型矩阵样本的特性，定义7中给出了基于集对信息粒的样本间距离度量方法.将该集对距离度量方法应用到k-modes聚类中，提出一种面向不完备分类型矩阵数据的集对k-modes聚类算法.在传统k-modes算法中，是用具有清晰边界的集合表示一个聚类，只考虑了样本与类簇之间的两种关系：属于和不属于，然而将不确定的样本分配到一个类簇会降低聚类结果的精确性.为此，本文在k-modes聚类算法的基础上进行改进，提出的集对k-modes聚类算法考虑了样本和类簇间的不确定关系，每个类簇由正同域Cs，边界域Cu和负反域Co表示.本文算法中涉及的相关定义如下：

定义8.(类内平均距离)：假设类簇Cj(1≤j≤k)中的样本数目为n，给定μj为类簇Cj的聚类中心，任意两个样本Xi，Xj间的距离为d(Xi，Xj)=1/[a+Shi(ρ)]，则类簇Cj内的平均距离为：

(9)

定义9.(阈值αj)：假设类簇Cj(1≤j≤k)的边界域中有n个样本，类簇Cj(1≤j≤k)的聚类中心记为μj，令样本Xi与聚类中心μj的距离为dij，样本Xi与其他类簇的聚类中心的距离中最小值为dih(1≤h≤k，h≠j)，则类簇Cj的阈值αj(1≤j≤k)为：

(10)

位于正同域中的样本肯定属于该类簇，且只属于这一个类簇，然而，位于边界域中的样本，可能与多个类簇存在关系，因此需要对每个类簇边界域中的样本进行计算判断.(dih-dij)表示样本Xi与所在类簇中心之间的距离和与其他类簇中心之间的最小距离的差值，该差值越大代表该样本距离其他类簇越远，属于其他类簇的可能性越小.

对于每个类簇，设定了一个阈值用于判断样本Xi是否与其他类簇存在关系，阈值αj的确定是根据(dih-dij)的均值，对于每个样本，若计算得到的差值比阈值小，说明该样本与其他类簇存在一定的关系，故将该样本也分配到其他类簇Ch的边界域中，使其同时位于两个类簇.

本文MD-SPKM算法将聚类过程主要分成以下几部分：

1)初始样本的划分

假设U={X1，X2，…，Xn}是一组n个矩阵样本的集合，从样本集U中随机选取k个矩阵样本作为初始聚类中心{μ1，μ2，…，μk}.根据公式(5)和公式(6)，将样本集中的每个样本Xi(1≤i≤n)与各聚类中心μj建立集对联系度.再根据集对距离公式(8)，得到每个样本与各个聚类中心的距离d(Xi，μj)，选择距离最近的聚类中心确定Xi的类簇标记λi=argminj∈{1，2，…，k}d(Xi，μj)，将样本Xi划入相应的类簇：Cλi=Cλi∪{Xi}.

2)聚类中心更新

3)集对聚类结果生成

C={{Cs(C1)∪Cu(C1)}，{Cs(C2)∪Cu(C2)}，…,{Cs(Ck)∪Cu(Ck)}}

其中，Cs(Ck)是类Ck的正同域，Cu(Ck)是类Ck的边界域，正同域和边界域共同构成一个类簇，聚类结果的示意图如图1所示.

图1 集对k-modes聚类示意图

算法具体实现流程如下：

算法.MD-SPKM

输入:样本集U={X1，X2，…，Xn}，类簇数目k

输出：集对聚类结果为：C={{Cs(C1)∪Cu(C1)}，

{Cs(C2)∪Cu(C2)}，…，{Cs(Ck)∪Cu(Ck)}}

1.从样本集U中随机选取k个样本，作为初始聚类中心{μ1，μ2，…，μk}；

2.令Cj=Ø(1≤j≤k)

3.fori=1，2，…，ndo

4. 根据公式(8)计算每个样本Xi与聚类中心μj的距离d(Xi，μj)，

令λi为簇标记；

5.λi=arg minj∈{1，2，…，k}d(Xi，μj)，将样本Xi划入相应的类簇：

Cλi=Cλi∪{Xi}；

7.Q是更新后的聚类中心；

8.end for

9.repeat

10.fori=1，2，…，ndo

11. 重新计算每个样本与当前类簇聚类中心的距离；

12. if存在样本与另一个类簇的距离更近then；

13. 将样本重新分配到该类簇，并更新这两个类簇的聚类中心；

14. else

15. 保持当前分配状态不变；

16. end if

17.end for

18.until没有样本改变类簇；

d(Xi，μj)进行比较；

22. 将样本划分到类簇Cj的正同域Cs；

23.else

24. 将样本划分到类簇Cj的边界域Cu；

25.end if

26.计算得到边界域中每个样本的(dij-dih)值，再根据公式(10)

获得阈值αj(1≤j≤k)；

27.if(dij-dih)<αjthen

28. 将样本Xi同时分配到类簇Cj和Ch的边界域中

29.else

30. 保持样本Xi当前分配状态

31.end if

32.returnC={{Cs(C1)∪Cu(C1)}，{Cs(C2)∪Cu(C2)}，…，

{Cs(Ck)∪Cu(Ck)}}

在上述算法中，步骤1-步聚5是根据本文在定义7中提出的集对距离度量方法，得到每个样本与各个聚类中心的距离，从而将样本分配到距离最近的类簇中；步骤6是在每次分配一个样本后，对聚类中心进行更新，使得目标函数最小化；步骤10-步骤17是将所有样本分配到类簇后，重新计算样本与各个类簇之间的距离，并将其优化为每个样本与所在类簇的距离是最近的.接下来，是对初步聚类结果进行细分，主要任务是构造正同域和边界域.在步骤19-步骤25中，根据定义8中给出的类内平均距离的定义，对各个类簇依次进行处理，将类簇中的样本划分到正同域和边界域；由于边界域中的样本有可能属于多个类簇，因此，在步骤26-步骤31中，根据定义9中的阈值计算公式，对边界域中的样本进行判断，若样本与多个类簇存在关系，将其同时分配到这些类簇的边界域；最后，输出包含正同域和边界域的集对聚类结果.

4.4 算法复杂度分析

由于在当下大多数实际应用场景下，数据具有大量的属性，会对算法的效率具有一定的影响，故令论域中样本数目为n，属性数目为m，类簇数目为k.本文算法的复杂度主要由两部分产生，第1部分是计算样本与各个聚类中心的距离产生的复杂度为O(kmn)，令迭代次数为t，则产生的时间复杂度为O(tkmn).第2部分是由对初步聚类结果细化，将每个样本划分到相应类簇的正同域或边界域产生，其时间复杂度为O(kmn).所以，整个MD-SPKM算法产生的时间复杂度为O(tkmn)+O(kmn).

5 实验评价

在这一部分中进行了一系列的实验，来评估所提算法MD-SPKM的聚类性能，通过选取4种代表性的算法进行了实验对比.第1种是Huang提出的经典k-modes算法[3]，第2种是Cao等提出的基于矩阵样本的k-mw-modes算法[8]，第3种是Li等提出的MD fuzzy k-modes 算法[17]，第4种是Saha等提出的基于粗糙集的Fuzzy k-modes算法[23]，将其记为RFKMd算法.

为了证明MD-SPKM算法的有效性，将从两个方面进行实验评价:1)以Microsoft Web数据集为例，对算法的性能进行分析；2)选择不完备的矩阵数据集，在不同缺失率的条件下，通过4个聚类评价指标，将本文所提算法MD-SPKM与4个对比算法进行比较分析.

本文在一台DELL计算机(Windows 10，Intel(R)Core(TM)i5-8300H，CPU@ 2.30 GHz 2.30 GHz)上实现了该算法和对比算法，编程平台为Python3.7.

5.1 数据集与评价指标

在本实验中，选择了3个数据集来评估算法，分别是Musk、Microsoft Web和MovieLens.Musk从UCI数据库下载，包含92个样本的476条记录值，每个样本有167个属性；Microsoft Web数据集也从UCI数据库下载，包含32711个用户对294个网站的165257条记录值，每条记录有用户ID，网页ID两个属性；MovieLens数据集在2018年创建，从MovieLens website下载，本文使用了其中的ratings数据，包含了6040名用户对3900部电影的1000209个评级分值，其中每条记录值有用户ID，电影ID，评分等级和提交时间4个属性.本文实验选择将不影响聚类结果的提交时间属性删除.由于具有标签信息的矩阵样本数据是比较少见的，因此，需要对给定的数据进行预处理，本文采用多维标度法对数据进行处理，预处理后的最终数据集如表2所示.

表2 矩阵数据集的描述

聚类的评价，也称为聚类有效性，是评价聚类算法性能的关键过程.以下评价指标常用于评价聚类算法的性能.

C={{Cs(C1)∪Cu(C1)}，…，{Cs(Ck)∪Cu(Ck)}}

1)准确率(Accuracy)

(11)

式(11)中，n为样本的总数，θk为簇Ck中正确划分的样本数目，包含正同域和边界域中的样本.

2)召回率(Recall)

(12)

式(12)中，TP表示真实为正，预测也为正的个数，FN表示真实为正，预测为负的个数.

3)调整兰德系数(ARI)

(13)

4)标准化互信息(NMI)

(14)

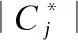
5.2 实验结果及分析

5.2.1 MD-SPKM算法性能分析

为了更好的展示本文所提算法MD-SPKM的聚类效果，以Microsoft Web数据集为例，给出了迭代过程中评价指标的变化情况.由于每个类簇都是由正同域和边界域构成，所以在图2(a)中给出了在4个评价指标下仅包含正同域Cs(Cj)的计算结果，在图2(b)中给出了在4个评价指标下包含正同域和边界域Cs(Cj)∪Cu(Cj)的计算结果.

图2 Microsoft Web数据集的迭代聚类过程

MD-SPKM算法可以做到考虑样本和类簇间的不确定关系，将肯定属于该类簇的样本划分到正同域，将可能属于该类簇的样本划分到边界域.从图2可以看到，随着迭代次数的增加，4个指标的结果都在不断上升.然而，在所有指标下，正同域和边界域结合的结果均高于仅考虑正同域的，其原因是每个类簇被划分为正同域和边界域两部分，这两个集合是通过基于二支聚类的收缩或扩展得到的.在图2(a)中得到的最优聚类结果是准确率0.9296、召回率0.9552、ARI 0.7383以及NMI 0.6405.在图2(b)中虽然仅考虑正同域，但准确率依然达到了0.8981，ARI达到了0.7，NMI达到了0.5856，仅召回率下降幅度稍大，下降为0.5994，但总体仍得到了较好的聚类结果.

5.2.2 不同缺失率下的实验对比分析

为了模拟含有缺失值的数据集，随机选择删除了一些样本的属性值.在实验中，选用5%、10%、15%和20%的缺失率随机生成不完备矩阵数据集，为了消除缺失数据结构或分布的影响，在每个缺失率下，生成多个不同的数据集，然后取多次运行得到的实验结果的平均值.本文选取了4种算法与所提算法MD-SPKM进行比较，这4种算法分别是k-modes[3]，k-mw-modes[8]，MD fuzzy k-modes[17]和RFKMd[23].通过4个评价指标对Musk、Microsoft Web和MovieLens数据集在不同缺失率下进行实验评价，其结果如表3-表5所示，每个数据集在不同缺失率下的最佳性能已用黑体突出显示.

表3 Musk数据集在4种缺失率下的聚类结果

从表3-表5中可以看到，在多数情况下，MD-SPKM算法比k-modes，k-mw-modes，MD fuzzy k-modes以及RFKMd算法具有更好的聚类性能，特别是在Microsoft Web数据集，在4种缺失率下实现了所有指标均高于对比算法，这也表明了MD-SPKM算法的优越性.表3中给出的是Musk数据集的实验结果，MD-SPKM算法在缺失率为5%和10%的条件下，得到的聚类结果均优于对比算法，在缺失率为15%时，虽然它不是最好的算法，但准确性也接近最好的对比算法.表5中给出的是MovieLens数据集在不同缺失率下的实验结果，可以看到在缺失率为5%、10%、15%和20%时，MD-SPKM算法在指标准确率、Recall和ARI下的结果均高于对比算法.另外，对于指标NMI，在缺失率为5%和10%的条件下，对比算法k-mw-modes达到了最好的效果，虽然MD-SPKM算法不是最优的，但也高于其他3个对比算法.

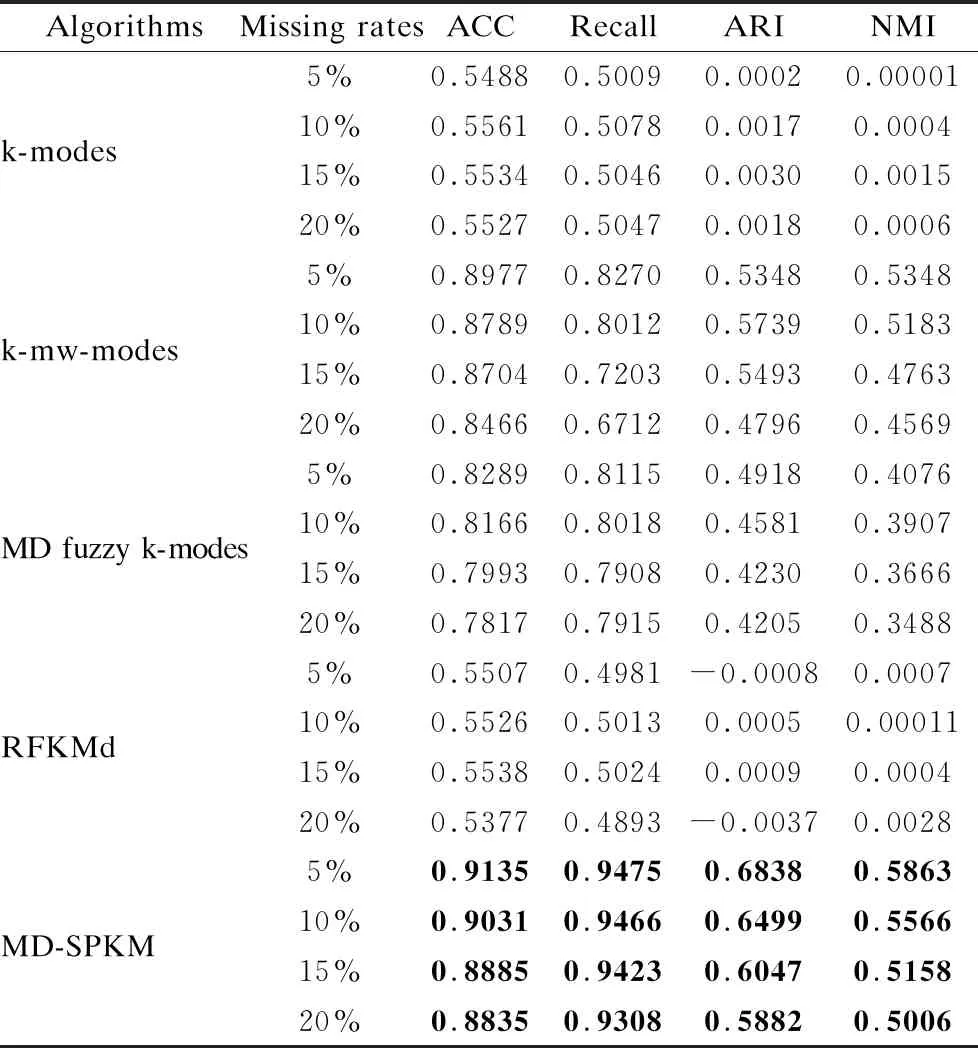
表4 Microsoft Web数据集在4种缺失率下的聚类结果

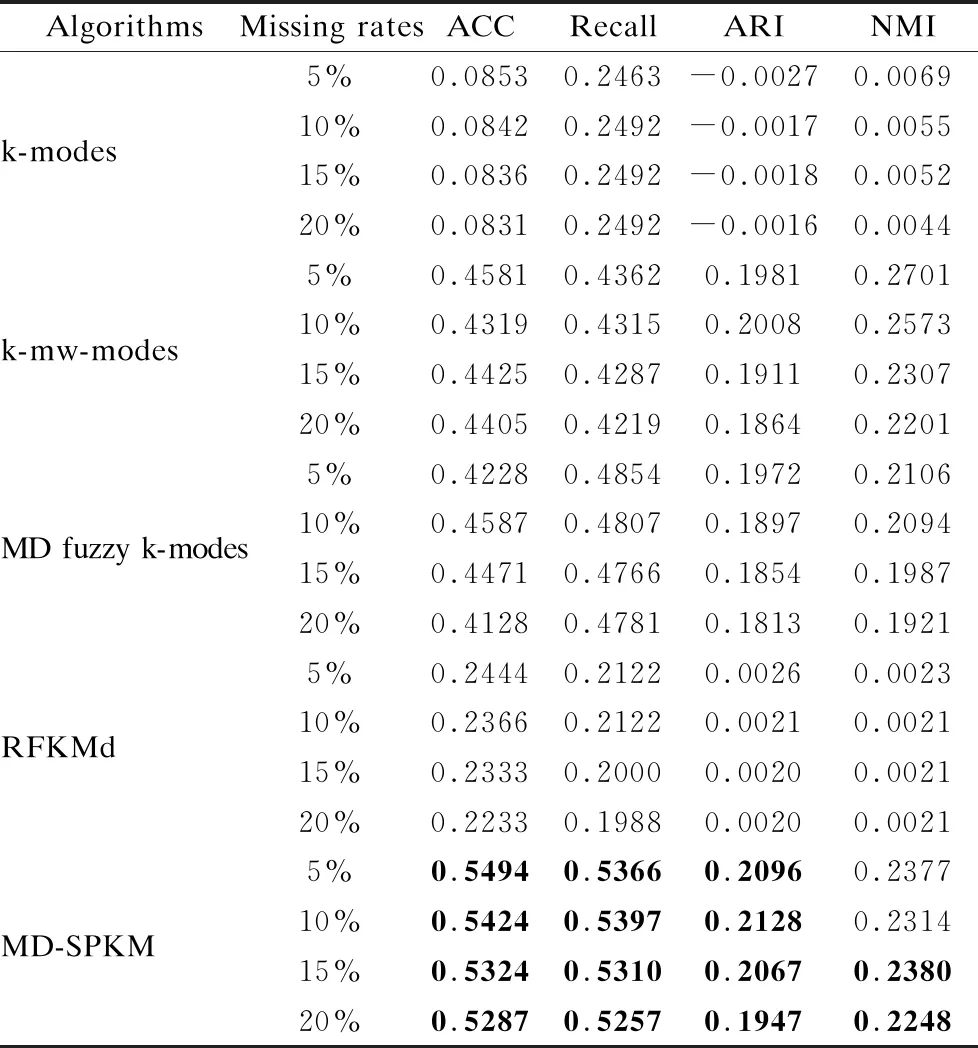
表5 MovieLens数据集在4种缺失率下的聚类结果

另外，从表3-表5中可分析出，在缺失率增加的情况下，本文算法和对比算法的准确性都呈现下降的趋势，导致下降的原因是缺失率越高，数据中的确定性信息越少，不确定性信息越多，相应作出错误分类的可能性就越高，这也与实际一致.

本文实验中选取的3个数据集都是不完备、矩阵数据集.由于对比算法k-mw-modes和MD fuzzy k-modes的研究对象都是完备矩阵数据集，未考虑缺失值对实验结果的影响.另外，对比算法RFKMd和k-modes，都是用于处理仅一组属性特征描述的数据集，不能充分考虑数据的所有信息.然而在本文中，根据集对信息粒理论，提出了一种可以处理不完备、矩阵数据集的距离度量方法，并对传统k-modes算法进行改进，从而实现了较对比算法性能的提升.

6 结 论

本文对传统k-modes算法进行改进，提出了一种面向不完备分类型矩阵数据的集对k-modes聚类算法.首先，对数据集中的缺失值给出了处理方法，采用集对信息粒的相关理论，对样本进行粒化处理，划分成正同粒、差异粒、负反粒，提出了矩阵样本间的集对距离度量方法.将聚类过程中不同样本之间的距离扩展成包含正同度、差异度和负反度3个维度的距离定义，由此将样本划分到各个类簇，形成初步的聚类结果.其次，考虑样本和类簇间的不确定关系，给出了类内平均距离的定义，用于将肯定属于类簇的样本与可能属于类簇的样本进行区分.另外，给出了判断样本是否属于多个类簇的阈值计算公式，对初步的聚类结果进行细分，形成包含正同域，边界域和负反域的集对聚类结果.最后，利用选取的3个数据集与四个对比算法进行实验评价，结果表明，本文所提MD-SPKM算法可以有效处理不完备矩阵数据集，并在多项评价指标下优于对比算法.