基于GMM 的说话人识别系统研究及其MATLAB 实现

何建军

（深圳电器公司 技术中心，广东深圳 518001）

0 引言

在现实生活中，很多情况下都需要验证人们的身份。随着人们交际范围的扩大，人际关系也变得日趋复杂，人们往往需要与其他各行各业的人打交道，而这些人际交往往往又会涉及到一些金钱、个人隐私等方面的私密信息。因此，要想保障双方正常且安全的交往，往往需要鉴定对方身份。

为此，人们进行了大量研究工作，试图寻找一种更可靠、方便的身份验证方法。与传统身份验证方式相比，生物特征认证具有更好的可靠性与安全性［1］。生物特征包括声纹、指纹、人脸、虹膜等。声纹（Voiceprint）是一种声波频谱，其中包含了相应的语言信息，查看时需用电声学仪器进行显示。与指纹识别、脸部识别、手指静脉识别等生物特征识别技术一样，声纹信息作为人的基本生理特征，有其独特优势。如声音是非接触性的，用户容易接受；声纹信息不需要记忆，因此不存在被遗忘的情况；其还具有独特性、唯一性和识别性强等特征。正因为具有以上优点，声纹信息作为一种身份验证方式获得了人们重视，并得到了广泛研究，声纹识别也应运而生。

说话人识别（Speaker Recognition，SR）也称为声纹识别、话者识别，属于生物特征识别技术的范畴，是一种通过声纹信息识别说话人身份的技术。其以表征说话人个性的语音特征为标准及依据，自动对说话人身份进行识别。

根据识别方式的不同，说话人识别可分为说话人探测跟踪、说话人辨认与说话人确认3 类［2］。

（1）说话人探测跟踪。说话人探测跟踪（Speaker Seg⁃mentation and Clustering）也称为说话人切分与聚类，是指在一段多人分时讲话的语音中，正确将切换到下一个人说话的时间标注出来。

（2）说话人辨认。说话人辨认（Speaker Identification）也称为说话人鉴别，是指从给定用户集中将测试语音所属的说话人辨认出来，是一个一对多的分析过程。说话人辨认又可划分为“闭集（待鉴别的说话人一定不在设定的说话人集合范围外）”和“开集（待鉴别的说话人可以不在设定的说话人集合范围内）”两种［3］。

（3）说话人确认。说话人确认（Speaker Verification）也称为说话人验证［4-7］，是指通过对声称者（即声称自己是真实说话者）所说的一段测试语音按照某种判决方式确认其是否为真实说话者，这是一个一对一的确认过程。

随着嵌入式软硬件技术与无线通信技术的迅猛发展，语音输入与控制将成为手持移动设备及嵌入式系统最佳的交互方式，以声纹信息为特征的身份鉴别技术也显得愈加重要。

1 相关研究

目前，针对说话人识别而提出的新的识别技术层出不穷，如结合GMM-UBM 结构［8］与支持向量机（Support Vector Machine，SVM）［9-10］的技术、基于得分规整技术的HNORM、ZNORM 和TNORM 技术、潜伏因子分析（Latent Factor Anal⁃ysis，LFA）技术、应用于说话人识别的大词汇表连续语音识别（Large Vocabulary Continuous Speech Recognition，LVC⁃SR）技术等。然而，如今最出色的说话人识别系统依然是基于GMM 模型，尤其是基于UBM-MAP 结构的系统。

本文基于TIMIT 语料库分析研究说话人语音信号预处理，以及说话人语音特征提取原理与方法，并利用MATLAB进行美尔频率倒谱系数（Mel Frequency Cepstrum Coeffi⁃cient，MFCC）［11］提取。在此基础上详细研究了GMM 模型基本原理，以及EM 算法和K-均值聚类算法，最后使用MATLAB 实现了基于GMM 模型的说话人识别系统，完成了GMM 模型参数训练与识别过程。为分析该系统性能，本文通过实验分析了不同GMM 模型阶数与不同训练语音样本时长对系统识别性能的影响。

2 说话人识别系统

2.1 说话人识别系统基本结构

一个完整的说话人识别系统建立与应用过程可分为模型参数训练阶段和结果识别阶段［12］。

模型参数训练阶段：首先对训练语音进行预加重、分帧与加窗等预处理，然后按照所选特征的计算方法对预处理后的语音信号提取特征参数，最后用提取出的特征参数估计模型参数集并进行存储，在识别阶段作为参考模型。本文设计的说话人模型训练框图如图1 所示。

Fig.1 Block diagram of speaker model training图1 说话人模型训练框图

结果识别阶段：前期处理与训练阶段相同，即首先对待识别的语音进行预加重、分帧及加窗等预处理，然后对预处理后的语音信号提取所选特征参数，接下来将这些特征参数与预先存储在计算机模板库中的参考模板或模型进行匹配计算，最后根据计算出的相似度，按一定准则输出匹配结果。本文设计的说话人识别框图如图2 所示。

Fig.2 Block diagram of speaker recognition图2 说话人识别框图

2.2 语音信号预处理

2.2.1 采样与量化

语音信号是一维模拟信号，其是一个幅度随时间不停变化的时变信号。要想在计算机上处理语音信号，必须先对其进行采样与量化，从而在时间和幅度上将其变成能在计算机上处理的离散的数字信号。

根据奈奎斯特定理，为使采样后的语音信号不丢失信息，采样频率必须设定为高于两倍的语音信号最大频率，才能用采样后的语音信号重新构造并还原出原始语音信号。在实际的语音信号处理过程中，采样频率一般取8～10kHz。在一些系统中为获取更高的识别率，采样频率可取15～20kHz。

采样后的语音信号因其在幅度上还保持连续，为使其幅度值也离散化，还需进行量化处理。一般用二进制表示量化值（即量化字长），倘若用B 个二进制数表示量化值，则：

式（1）表明：量化器中每个bit 对信噪比的贡献大约为6dB，当量化字长为10 bit 时，信噪比为53dB。由于语音信号信噪比可达55dB，因此应选择大于10 bit 的量化字长。

2.2.2 语音信号预加重

经过采样与量化后的语音信号还要进行预加重处理，因为语音信号在高频处会有能量损耗，为弥补这些高频损失，须在预处理过程中进行预加重以提升高频部分。

可在A/D 转换之前进行预加重处理，不仅可达到预加重目的，而且可达到对语音信号动态范围进行压缩处理、提高语音信号信噪比的目的。也可在A/D 转换之后进行预加重处理，即利用能对高频特征进行提升的具备6dB/倍频程的数字滤波器［13］进行预加重处理。该数字滤波器的Z传递函数如下：

式中，a为预加重系数，其值接近于1，如取a＝0.937 5。

对于待处理的语音信号，可用以下公式进行预加重：

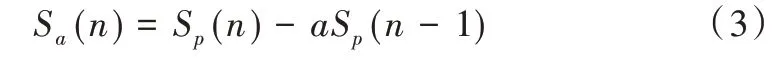
式中，Sa为预加重操作前的原始语音信号，Sp为预加重操作后的语音信号。

2.2.3 语音信号加窗分帧

语音信号幅值是随时间变化而发生变化的，其不是一个稳态过程［14］，而是属于时变信号。但是，在短时段上可认为声道形状、激励性质保持不变，因此可采用稳态过程分析方法进行语音信号分析。短时分析的前提是获取短时语音，即对输入语音进行划分小段操作，也即加窗。窗函数对语音信号进行分段操作，移动窗函数即可获得语音信号的一个个短时段。其中，一个短时段作为短时分析的一帧，一般而言，在一个短时段内语音信号基本保持稳定，声道参数基本不发生变化。通常该短时段（也即一帧语音时长）取值范围为10～30ms。

为从每一帧中取出含有N 个样本的语音信号序列，可将窗函数w(n)与原来的语音信号S(m)相乘。加窗运算定义为：

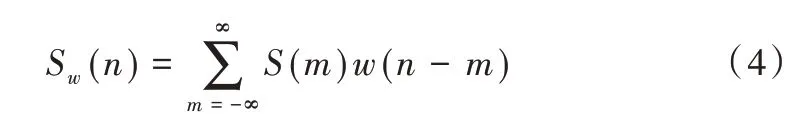
设窗口长度为N，窗函数主要分为以下几种：

（1）矩形窗。

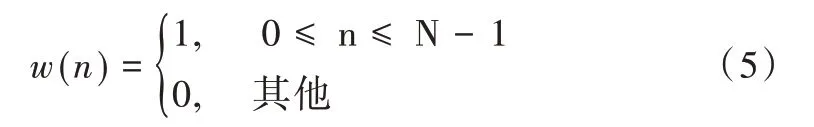
（2）汉明窗（Hamming）。

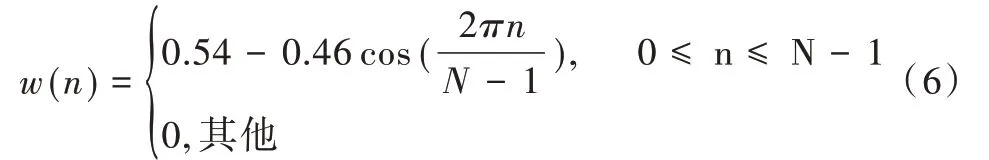
（3）汉宁窗。

本文使用的是汉明窗。为使语音信号变化的信息尽可能不丢失，可采用相邻两帧之间有部分相互重叠的分段方法进行分帧（即相邻两帧语音信号的前一帧语音信号末端与后一帧语音信号前端相重叠），令相邻两帧之间可最大程度地保留语音信号变化信息，从而使相邻两帧的过渡更加平滑。相邻两帧之间的重叠块称为帧移，其帧移量取值范围一般为帧长（即窗口长度）的1/3～1/2。加窗以后得到的一帧语音采样序列为：

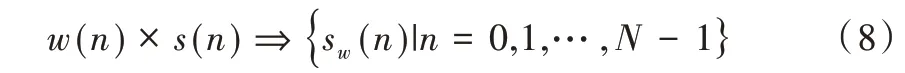
2.3 语音信号特征提取

实验表明，能对说话人个性有效进行描述的特征有：短时能量、短时平均幅度、短时平均过零率、短时频谱、短时基音周期及基音频率、共振峰频率及带宽、部分相关系数（PARCOR）特征、线谱对（LSP）特征、线性预测系数（LPC）、倒谱特征、美尔频率倒谱系数（MFCC）等。下面介绍两种主流的表征说话人个性的线性预测系数和美尔倒谱系数特征提取过程。

2.3.1 线性预测系数（LPC）

线性预测［15］分析可这样理解：对于一个语音信号，其某个时刻的采样值可通过该时刻之前若干时刻的采样值进行线性逼近。为得到一组最优的预测器系数，可在最小均方误差上使线性预测计算得到的数值与实际语音采样值逼近，而预测器系数就是过去若干时刻采样值线性组合的加权系数。这种线性预测分析技术最早在语音编码中使用，因此线性预测系数也常被人们称为LPC（Linear Pre⁃diction Coding）。

可将p 阶线性预测器从时域角度理解为：采用语音信号前p 个时刻采样值的线性组合，并以最小预测误差预测当前时刻样本值。即的预测值为：

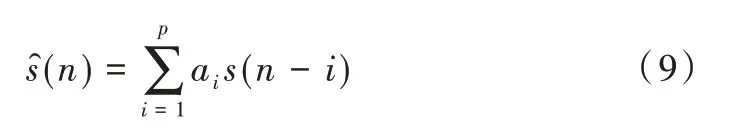
对上式进行Z 变换，得到具有如下形式的传递函数滤波器输出：

式中，A（z）为预测误差滤波器。

为得到一组最优的预测器系数，假设E 为语音帧上所有的预测均方误差：

进行线性预测分析的前提是用于分析的语音信号具备短时平稳特征，也即是说必须在一段短时语音段上进行，即按帧进行。大量实践证明：LPC 参数是一种表征语音信号特征的良好参数。

2.3.2 美尔倒谱特征（MFCC）

美尔频率倒谱系数（MFCC）［16-18］是采用先将语音功率谱转换成Mel 频率对应的功率谱，再进行滤波取对数，最后进行离散余弦变换的方法求取出来的，人们对频率在1kHz以下声音的感知依从线性关系，而对频率在1kHz 以上声音的感知依从近似的对数频率线性关系。由此划分语音频率，将其划分成一系列三角形的滤波器序列（即Mel 频率滤波器组），这组滤波器在频率的美尔（MEL）坐标上是等带宽的。Mel 频率与实际频率的转换关系为：

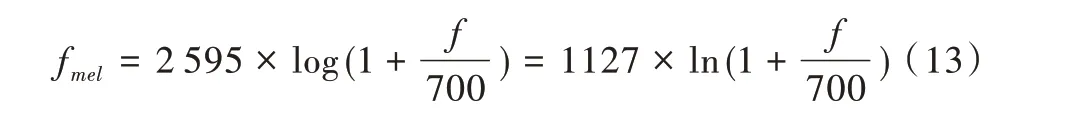
式中，f为实际频率，单位为Hz。

MFCC 系数的计算是按帧进行的，首先将语音信号进行分帧、预加重与加窗，然后进行FFT 变换，计算出该语音帧的功率谱，再将其功率谱变换为对应于Mel 频率的功率谱。在进行Mel 功率谱变换之前，需要先设置若干个三角形带通滤波器，且带通滤波器必须在语音信号频谱范围内。该滤波器组的中心频率f(m),m=0,1,…,M-1 均匀分布Mel 频率坐标轴上。

三角形带通滤波器系数在计算MFCC 系数之前必须预先计算出来，计算MFCC 系数时直接使用该系数。Mel 带通滤波器的传递函数为：

（1）预处理：为了对语音信号进行短时分析，需将短时语音段时长设定在10～30ms 范围内，即确定每个语音帧的采样点数，进而对每个语音帧进行预加重与加窗分帧操作，并计算出其时域信号x(n)。

（2）离散FFT 变换：对于信号x(n)，为了计算其频谱X(k)，需对其作离散FFT 变换，则有：

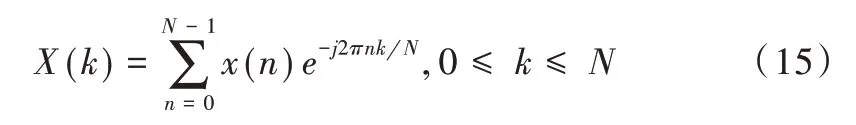
式中，N 为FFT 变换点数。

（3）计算能量谱：对频谱取模的平方，得到其能量谱|X(k)|2,0 ≤k≤N。

（4）在频域上对能量谱进行滤波：用M 个Mel 带通滤波器对能量谱进行滤波，对于每个带通滤波器，对其频带范围内所有能量进行叠加处理，即可得到M 个能量谱输出：

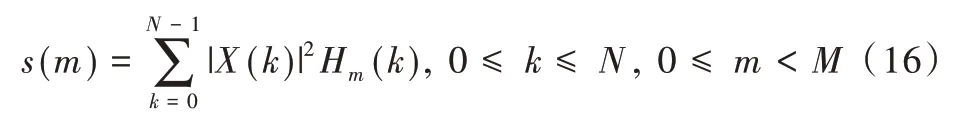
（5）对滤波器组输出的能量谱取对数：对能量谱s(m)取自然对数，可得到其对数功率谱S'(m)为：

（6）离散余弦变换：在对数功率谱S'(m)上进行离散余弦变换，得到M 个MFCC 系数，即：

在进行MFCC 系数选择时，可舍去代表直流成份的C0，取L 个参数作为MFCC 参数。一般L 取12～16，其计算流程如图3 所示［19］。

本文采用MFCC 系数作为特征参数。

Fig.3 MFCC parameter calculation flow图3 MFCC 参数计算流程

2.4 高斯混合模型

2.4.1 模型描述

高斯混合模型（GMM）本质上是一种多维概率密度函数，其核心思想为：在概率空间上，其特征向量的分布情形可用若干个单高斯概率密度函数进行线性逼近。将其用于说话人识别时，每个说话人对应一个GMM。

一个M 阶的GMM 模型概率密度函数是通过对M 个高斯概率密度函数的加权求和得来的，如下所示：

式中，λ 表示模型参数集，由均值、协方差、权重组成；o表示K 维特征参量；i表示高斯分量序号。GMM 模型阶数为M，表示有M 个高斯分量。P(o|q=i,λ)可简化成P(o|i,λ)的形式，表示序号为i的高斯分量，对应分量i的概率密度函数。Ci对应于第i个高斯分量的混合权重，也即先验概率。则有：

对于高斯分量i，常用一个维数为K 的单高斯概率密度函数进行描述，即：

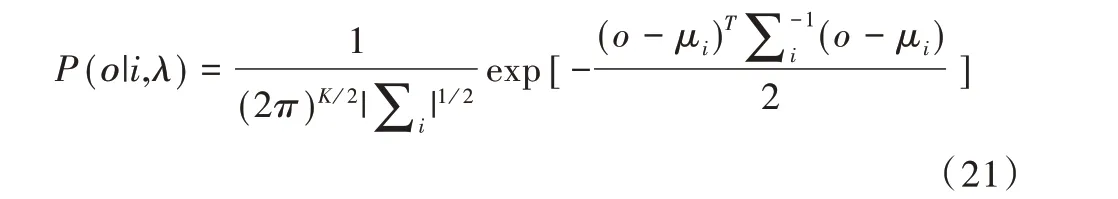
式中，μi为均值矢量，Σi为协方差矩阵，i=1,…,M。

GMM 模型参数集λ 的表达形式如下：

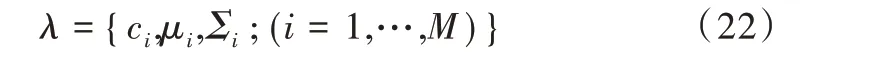
式中，λ 由各均值矢量μi、协方差矩阵Σi及混合分量的权重组成。其中Σi可以选择普通矩阵，也可以选择对角矩阵，但由于后者的算法简单且性能较好，为减少计算量，Σi通常取后者［20］。即：

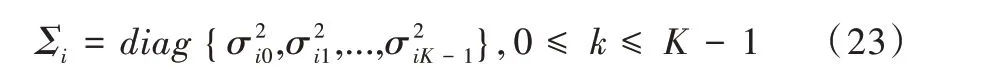
将式（23）代入式（21）可得：

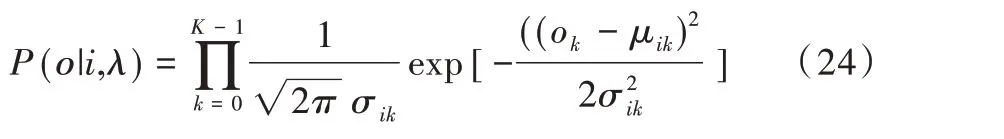
式中，ok、μik分别为矢量ο和矢量μi的第k个分量。

根据公式，GMM 观察特征矢量与模型匹配的基本框架如图4 所示。

2.4.2 模型参数估计

为说话人建立GMM 模型，实际上就是通过模型训练对GMM 模型参数进行估计，使其能最佳地匹配训练特征矢量分布。估计GMM 模型参数的方法有很多，本文采用最常用的最大似然（Maximum Likelihood，ML）估计法。该方法的前提条件是：给定训练数据以估计GMM 模型参数，且使估计出模型的似然值达到最大。对于T 个训练矢量序列ο={o1,o2,…,oT}，GMM 的似然值可用下式表示：

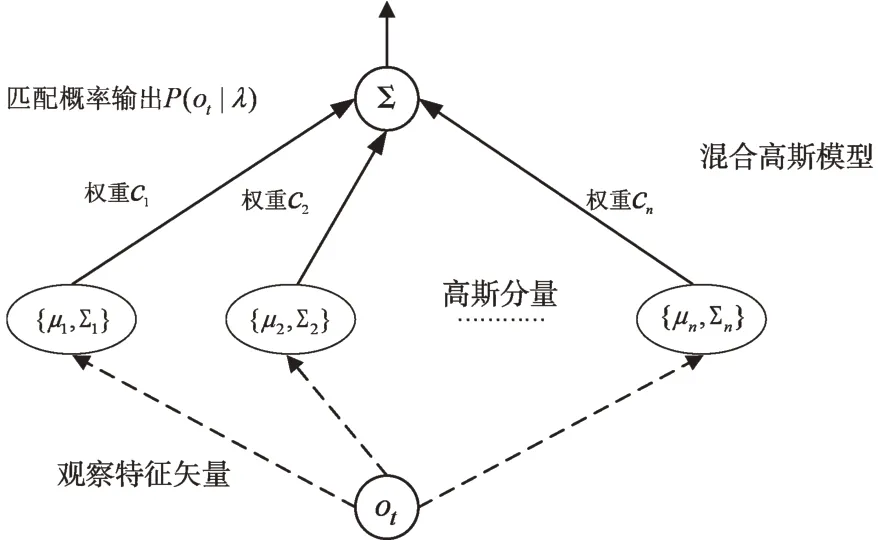
Fig.4 Basic frame of the observation feature vector of the GMM model and the model matching图4 GMM 观察特征矢量与模型匹配基本框架

由于似然函数P(o|λ)与模型参数集λ是非线性函数关系，很难直接求出上式的极大值点，必须引入隐状态参与计算。因此，为估计模型参数集λ，本文引入期望最大化算法（Expectation Maximization，EM）。EM 算法包含两个步骤：EStep 和M-Step。E-Step 也即人们求期望（即Expectation，用E 表示）的步骤，M-Step 将E-Step 所求的期望最大化（即Maximization，用M 表示），重复E-Step和M-Step直到收敛。

EM 算法估计过程为：从一个初始模型开始，利用最大似然准则，迭代地估计模型参数，使再以作为新的模型参数开始下一轮迭代过程，直到满足收敛条件。可引入辅助函数

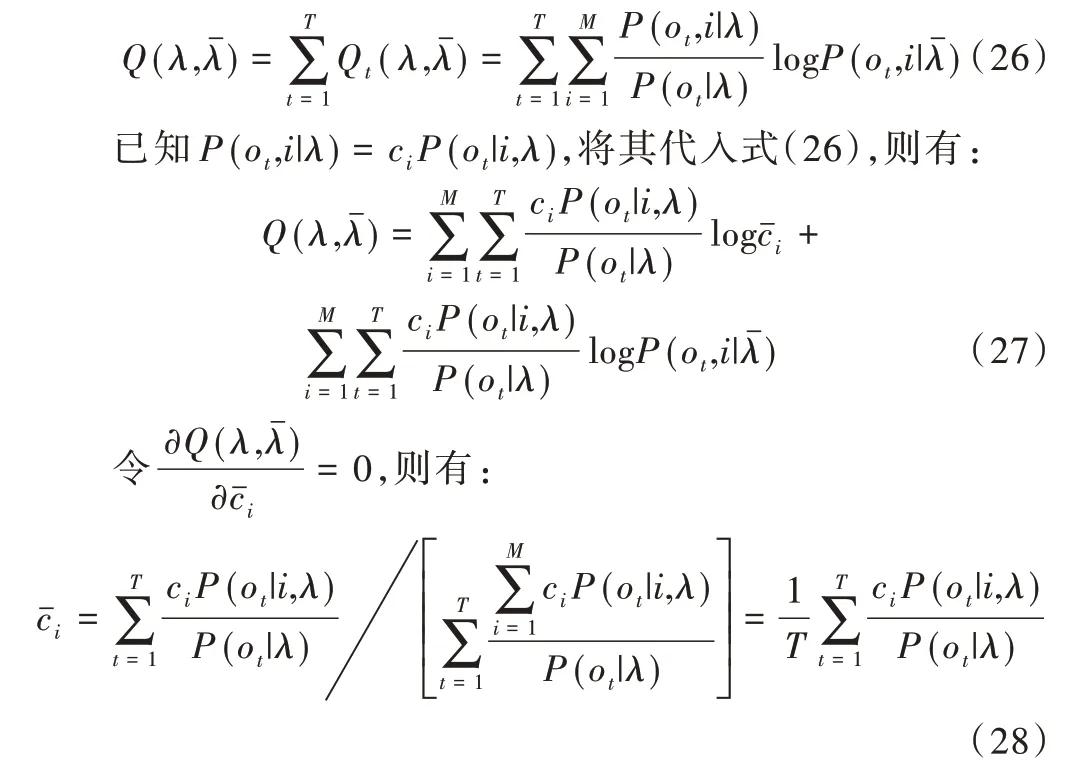
这样即可将迭代估计GMM 模型参数的过程分为Ex⁃pectation 和Maximization 两 个 步 骤，即E-Step 和M-Step。E-Step 计算训练数据落在隐状态i的概率，M-Step 以局部最大准则估计GMM 模型参数集也即

EM 算法计算过程如下：

（1）E-Step ：以Bayes 公式为依据和基础，计算训练数据对应于高斯分量i的概率。

E-Step 与M-Step 反复迭代，直至满足收敛条件，即可得到最优的模型参数λ。

在实际训练过程中，通常训练数据较少，训练环境背景噪声较大，语音易受到噪声污染，此时便很可能出现值过小的情况。然而，过小的方差会极大程度上影响对整体似然函数的计算。为避免该情况的发生，必须限制方差范围。即：

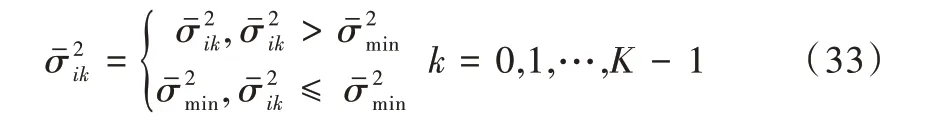
采用EM 算法估计GMM 模型参数的流程如图5 所示。

Fig.5 Flow of estimating GMM model parameters by EM algorithm图5 EM 算法估计GMM 模型参数流程

2.4.3 模型参数初始化

EM 算法迭代过程是从一个初始模型开始的，初始模型参数集λ的选择会影响算法迭代速度，其根本原因在于EM 算法是一个局部最优搜索算法，经过反复迭代可求出一个最佳解。GMM 模型常用的初始化方法有两种：①在训练数据中任意取出与M 个高斯分量相对应的M 组数据，分别计算出每组数据的均值和方差，且将其作为高斯分量的初始均值和方差，并使各分量权重相同；②通过K-均值聚类算法［21］对模型参数进行初始化，并划分训练数据到M 个聚类中，每个高斯分量对应一个聚类，各个高斯分量的初始均值为对应聚类的均值，且每个高斯分量方差与对应聚类方差相同，而对应聚类内的数据量与总数据量的比值即为权重。

GMM 阶数M 的选择与实际应用有关，一般由实验结果确定。K-均值聚类算法［22］的基本思想为：对于给定的样本集（即训练数据特征矢量集），按照样本之间的距离大小将样本集划分为M 个类别，使得类别内的样本尽量紧密聚集在一起，而类别间的样本距离尽可能大，并选择M 个初始聚类中心，按最小距离原则将各特征矢量xi逐个分配到M 类中的某一类，之后不断计算类的中心及调整各特征矢量类别，最终使各特征矢量距离其所属类别中心的平方和最小。具体计算步骤如下：

（1）在训练数据特征矢量集中任选M 个样本作为初始聚类中心：令k=0。

（3）计算重新分类后的各类中心。

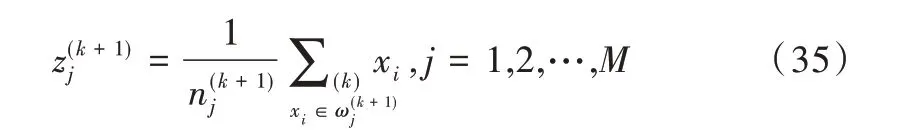
2.4.4 识别判决

对于一个有N 个人的说话人识别系统，用λi(i=1,2,…,N)代表第i个说话人的GMM 模型。在进行识别时，假设待识别语音的观察特征矢量序列为ο={o1,o2,…,oT}，则判定该目标说话人为第n 个说话人的后验概率为［23］：

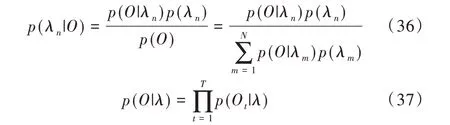
式中，p(O|λn)表示第n 个说话人产生O的条件概率，p(O)表示全部说话人条件下出现O的概率，p(λn)表示第n个说话人的先验概率。

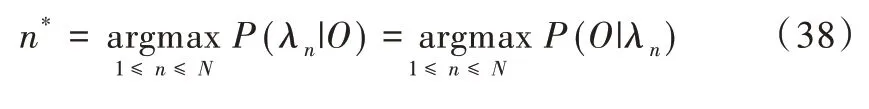
为简化计算，通常采用对数似然函数，则闭集说话人辨认的得分公式为：

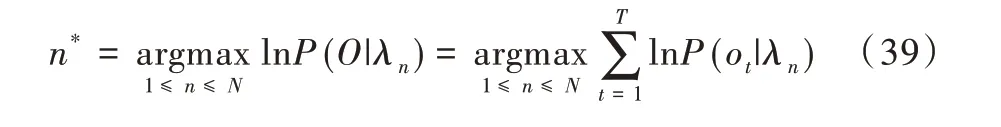
3 系统实现

3.1 实验环境

本文主要在HP 540 笔记本电脑上实现基于GMM 的说话人识别系统，该笔记本电脑的主要软硬件配置如下：①CPU：Intel（R）Core（TM）2 Duo CPU T5470 @ 1.60GHz；②RAM：2GB；③操作系统：Windows XP Professional；④实验环境：MATLAB R2009a。

3.2 语音库

本文说话人识别实验是在部分TIMIT 语音库基础上进行的，美国的LDC（Linguistic Data Consortium）第一个发布了拥有大量说话人的全英文语音数据库TIMIT，因而TIMIT被广泛应用于说话人识别研究［24］。TIMIT 语音库由美国麻省理工学院（MIT）、SRI 国际公司（SRI）与德州仪器公司（TI）共同设计，并在TI 完成录音［25］。其是在低噪声环境下使用固定麦克风录制的，采样频率为16kHz，采样位数为16位。录音人数共有630 人，其中男性438 人，女性192 人，每人讲10 句话，囊括了美式英语的八大方言。该语音库可以很好地区分性别、年龄段和地域。

为对比中英文语音库在识别性能方面的差异，另选部分HI-MIA 语音库进行对比实验。HI-MIA 语音库为昆山杜克大学与AISHELL 共同推出的一个基于远场文本相关的说话人认证数据库。该数据库使用麦克风阵列和Hi-Fi麦克风在实际家庭环境中收集数据，共包含340 个说话人，每个说话人语料包含了近场麦克风拾音和远场麦克风阵列的多通道拾音，可用于声纹识别、语音唤醒识别等研究。

3.3 系统在MATLAB 下的实现

本文在MATLAB 下实现了基于GMM 模型的说话人识别系统，程序运行界面如图6 所示。该系统主要分为两大部分：训练部分与识别部分。

Fig.6 MATLAB program running interface of speaker recognition system图6 说话人识别系统MATLAB 程序运行界面

训练时首先设置特征向量和GMM 模型参数，然后点击“选择训练语音”按钮选择训练语音文件，最后点击“建立模型”或“继续训练”按钮进行模型训练，并保存模型参数，如图7 所示。

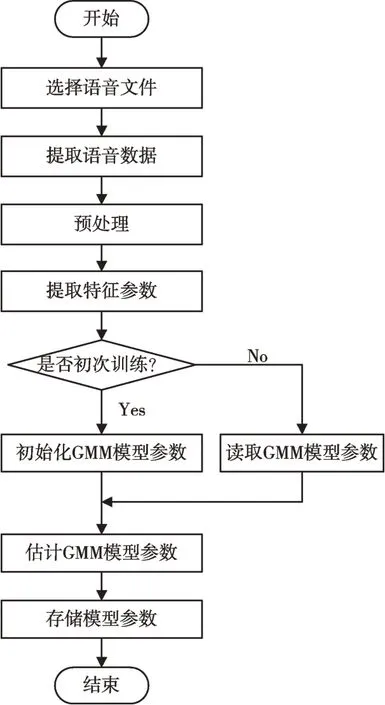
Fig.7 Model training flow图7 模型训练流程

识别时同样需要先设置特征向量和GMM 模型参数，然后点击“选择测试语音”选择待识别的语音文件，最后点击“识别”按钮进行识别并输出匹配结果，如图8 所示。

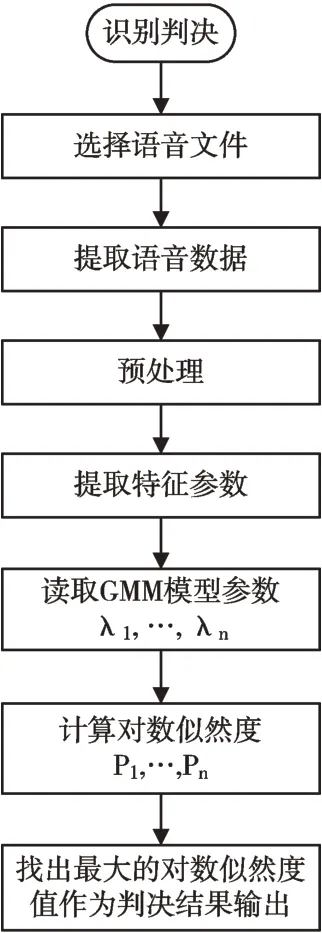
Fig.8 Speaker recognition flow图8 说话人识别流程

3.4 训练阶段

在进行模型参数训练之前，先建立一个GMM 模型，并为GMM 模型分配存储空间。每个GMM 模型存储内容包括特征矢量维数、高斯分量混合数，以及各高斯分量的权重、均值矢量与方差矩阵。

建立模型后进行模型训练，从说话人语音中提取语音样本，对语音信号进行预加重、分帧加窗与端点检测处理，提取出特征参数矢量，并用K-均值聚类算法对提取出的特征矢量进行聚类，得到GMM 模型的初始化模型参数λ（均值、混合权重及协方差矩阵）。初始化后即开始进行说话人GMM 模型训练，本文采用期望最大化（EM）算法估计GMM 模型参数，从一个初始模型参数λ开始，估计出一个新的模型参数λˉ，使得在新模型参数下的似然度P(o|λˉ)≥P(o|λ)。之后再采用新模型参数λˉ开始下一次迭代，如此反复迭代直至模型收敛（本文设置的收敛界限为1.000 0e-004）。具体实现流程如图9 所示。

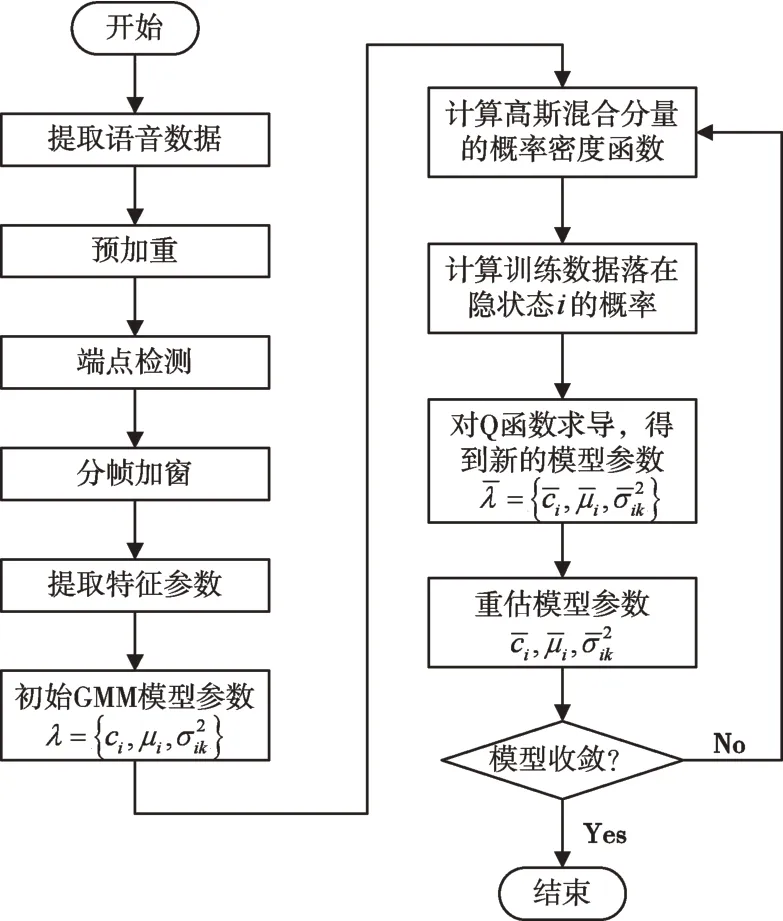
Fig.9 GMM model training flow图9 GMM 模型训练流程

3.5 识别阶段

本文采用闭集说话人识别方式，即将所有参与的说话人构成一个集合，在识别时判断目标说话人为集合中的哪一个说话人。

3.6 系统性能

实验从TIMIT 语音库中随机选取20 人的语音作为样本，对说话人识别系统性能进行测试。实验条件如下：①采用部分TIMIT 语音库，使用16 阶GMM 模型；②MFCC特征阶数为10、12、14、16；③测试数据为1 段语音，每段平均时长为4.5s；④测试人数为10、13、16、20；⑤训练数据为3 段语音，每段平均时长为4.5s。

说话人识别系统平均识别率如表1 所示。从表1 可以看出，系统性能随着特征向量维数、测试人数的变化而变化，即识别率随着特征向量维数的增加而提高，随着人数的增加而降低，但特征向量维数达到一定值时识别率便不再增加。当测试人数超过16 人时，特征向量维数为12 时识别率最高。

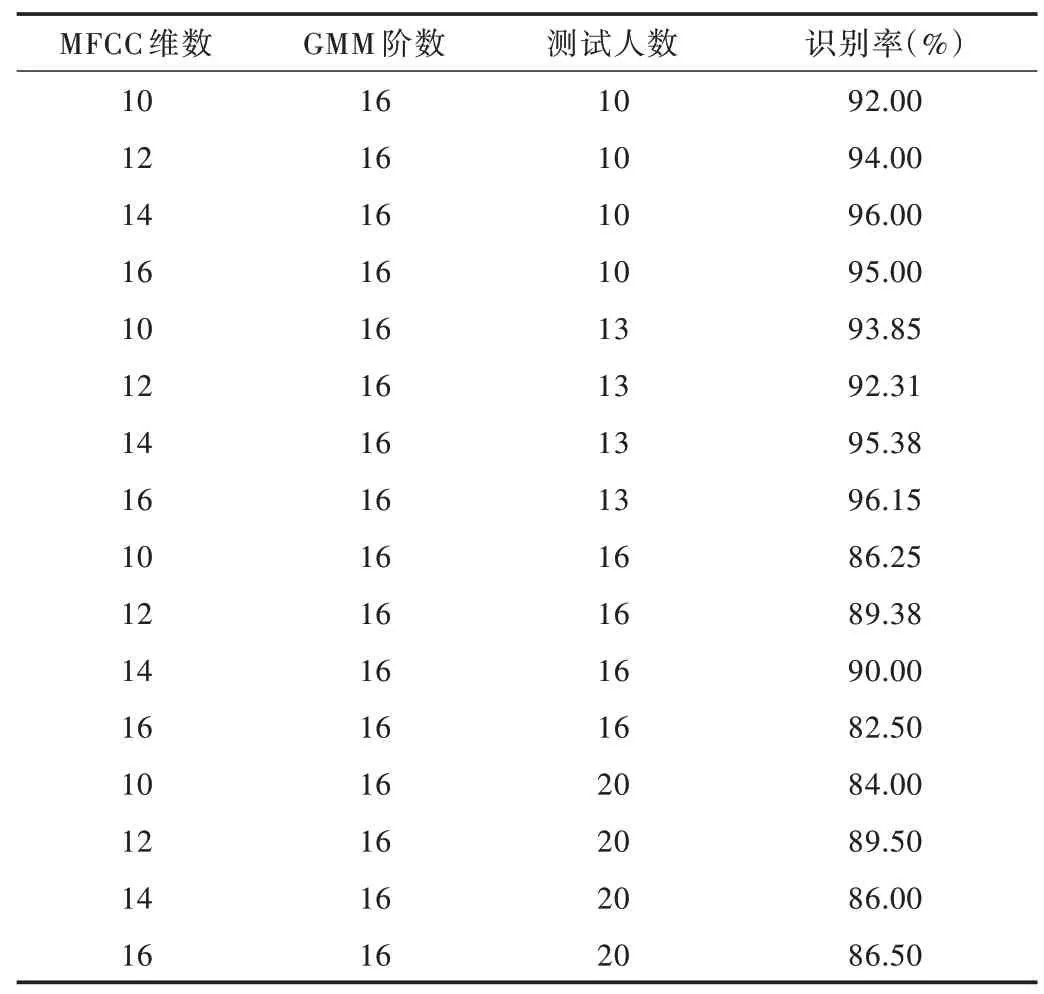
Table 1 Average recognition rate of the speaker recognition system表1 系统平均识别率

3.7 实验结果分析

3.7.1 GMM 模型阶数对系统识别性能的影响

GMM 模型阶数也即高斯分量个数，是影响系统识别性能的一个重要指标。若阶数过小会使量化误差过大，导致GMM 模型无法很好地表示整个向量空间；若阶数过大，则系统训练与识别计算量会非常大，却无法明显提高系统性能。因此，选择一个合适的GMM 模型阶数能显著提升系统综合性能。本文针对GMM 模型阶数对系统性能的影响作了如下实验。实验条件如下：从TIMIT 语音库中选取16 人的10 段语音作为样本数据，平均每段语音时长为4.5s，其中每人选取4 段语音作为训练数据来训练模型；另选1 段语音作为测试数据，选择24 维MFCC 系数作为特征参数，采用EM 算法训练模型，每段测试语音作为一个测试单位，取测试结果的平均值作为系统平均识别率。对不同GMM模型的阶数测试结果如表2 所示。

Table 2 Speaker recognition rate based on different order of GMM mode（lTIMIT）表2 不同GMM 模型阶数下说话人识别率（TIMIT）

从实验结果可以看出，GMM 模型阶数越高，对特征空间的描述越精确。阶数较低时，识别率较低；随着阶数的增加，识别率随之上升，系统计算量也急剧增大。但当阶数达到16 附近时，识别率则不再提升，反而还出现了下降趋势，这是符合倒谱特征性质的。因此，在综合考虑系统总体性能的基础上，选择一个合适的GMM 模型阶数是很重要的。一般来说，阶数不能取得过高，但也不能太低，往往需要大量实验数据来确定。

为对比GMM 模型阶数对系统识别性能的影响，另选部分中文语音库HI-MIA 中的数据进行对比实验。实验条件如下：从HI-MIA 语音库中选取20 人的20 段语音作为样本数据，平均每段语音时长为1s；任选其中一段作为测试数据，选择24 维MFCC 系数作为特征参数，采用EM 算法训练模型，每段测试语音作为一个测试单位，取测试结果的平均值作为系统平均识别率。对不同GMM 模型的阶数测试结果如表3 所示。

Table 3 Speaker recognition rate based on different order of GMM model（HI-MIA）表3 不同GMM 模型阶数下说话人识别率（HI-MIA）

3.7.2 训练语音时长对系统识别性能的影响

对GMM 模型的训练需要一定时长的训练语音数据，若训练数据太少，模型训练不充分，则不能得到有效的GMM模型；若训练数据太多，将浪费大量训练时间和系统资源，且识别率也不能得到相应提升，有时还会因过训练导致系统识别性能下降。本文针对不同训练时长下训练的GMM模型识别性能进行测试。

实验条件如下：从TIMIT 语音库中选取16 人的10 段语音作为样本数据，平均每段语音时长为4.5s；任选其中一段作为测试数据，在GMM 模型阶数为16、MFCC 系数维数为24、人数不变的情况下，分别用不同时长的语音训练GMM模型，取测试结果的平均值作为系统平均识别率。实验结果如表4 所示。

Table 4 Speaker recognition rate based on different training durations表4 不同训练时长下说话人识别率

从实验结果可以看出，增加训练时长可从总体上提升系统识别率，但到一定程度后便很难继续提升。因此，在训练模型时不应过度追求训练时长。

为对比训练语音样本时长对系统识别性能的影响，另选部分中文语音库HI-MIA 中的数据进行对比实验。实验条件如下：从HI-MIA 语音库中选取20 人的20 段语音作为样本数据，平均每段语音时长为1s；任选其中一段作为测试数据，在GMM 模型阶数为16、MFCC 系数维数为24、人数不变的情况下，分别用不同时长的语音训练GMM 模型，取测试结果的平均值作为系统平均识别率。实验结果如表5所示。

Table 5 Speaker recognition rate based on different training durations表5 不同训练时长下说话人识别率

4 结语

说话人识别技术作为一种有效的身份识别技术，为身份确认提供了一种极佳的验证手段。随着嵌入式软硬件技术与无线通信技术的迅猛发展，语音输入与控制将成为手持移动设备及嵌入式系统最佳的交互方式，以声纹信息为特征的身份鉴别技术也受到越来越多关注。

本文首先对语音信号预处理及特征提取进行了详细分析，然后以高斯混合模型作为说话人模型，对模型参数估计、模型参数初始化以及GMM 模型参数训练与识别方法进行了详细研究，最后，基于TIMIT 语料库使用MATLAB 实现了一个完整的说话人识别系统，并通过实验分析不同模型参数及不同训练时长对系统性能的影响。实验结果表明，在GMM 模型阶数不高及使用人数不多的情况下，本文实现的说话人识别系统可满足用户的使用需求。

未来针对该系统还有一些问题需要继续深入研究，例如：优化特征参数，以提升系统识别性能；通过模型参数估计算法或识别算法减小计算量，以缩短训练或识别时间；将GMM 模型与其他模型相融合，从而提高系统识别率等。