基于作息时空特征优化神经网络的出租车乘客候车时长预测
雷永琪,李 娜,陈智军,何 渡,张雨昂
(1.湖北大学 计算机与信息工程学院,湖北 武汉 430072;2.湖北省科技信息研究院,湖北武汉 430071)
0 引言
新一代智慧城市环境下,传统交通系统逐渐转变为融合了技术支持、城市建设和交通变革的“智慧出行”[1]。作为城市的主要交通工具之一,出租车具有灵活和便捷等特点,可以满足居民出行的一般搭乘需求[2]。然而,由于城市交通的动态时空变化及司乘信息不对称等因素,出租车规模量和居民打车需求之间经常出现供需不平衡现象,大中型城市的居民出行普遍存在出租车等待时间长、打车困难等问题,亟需合理有效的解决方法[3]。
当前,绝大多数城市出租车都已具备GPS 定位设备,这使得出租车行车轨迹数据大量可得。海量出租车轨迹数据蕴涵着丰富的行驶规律,常被用来研究城市居民活动规律或城市画像。郑宇[4]提出“城市计算”理念,开启了GPS轨迹数据挖掘的潮流;Deng 等[5]使用联立方程模型基于城市整体的出租车数量、计价,乘客数量、等候时间等进行建模;基于网络模型,Yang 等[6]对大面积区域之间的乘客流动进行建模,进而分析出租车运营的供求关系,并在供求平衡计算时对乘客的等候时间进行了预测;齐观德等[7-8]以概率为落脚点,重新定义了出租车乘客候车时间,根据出租车历史轨迹对某地某时段的候车时间进行建模,通过建立空驶出租车到达时间间隔的概率模型预测候车时长;Yuan 等[9]和Ma 等[10]基于改进的地图匹配低频采样算法ST-Matching,提出基于投票表决的地图匹配算法IVMM 和基于非齐次泊松过程的出租车乘车推荐模型,设计实现了T-Finder 系统、T-Share 系统,通过“拼车”解决出租车载客高峰期打车难的问题;Luis 等[11]提出一种使用增量规则的增量框架,给出一种能实时预测出租车乘客需求量的办法;单雄宇等[12]通过分析出租车轨迹数据,通过聚类算法提取出租车载客热点和计算空车到达时间,建立了对特定时间的特定载客热点区域的乘客候车时间预测模型;王诏远等[13]结合修复的GPS 数据和经验分布规律,计算出在等待特征点和时间点的打车概率,并且建立了等待时间模型;朱东杰[14]在车载自组织网路由协议及路径决策模型研究中,将车载自组织网络(VANET)和海量出租车轨迹数据结合,模型基于最大似然估计将车辆到达率近似为分段线性函数,预测出租车乘客打车概率与打车等待时间;刘仰东等[15]在基于车流量的司乘推荐模型研究中,提出基于出租车轨迹的出租车流量模型,并利用综合时间、天气等因素优化模型,建立车流量与打车概率、等车时间之间的函数关系,以预测用户所在位置的打车概率和等待时间;吕明等[16]通过对比小区内空驶出租车的总量与居民出行需求量,根据每个小区中不同的标记状态计算其乘客平均等待出租车的时间,该方法适用的研究区域有一定要求。
现有研究成果能够为城市居民打车提供一些科学的参考依据,但主要采用的是聚类和建模等传统手段,尚未充分挖掘并利用出租车的行驶规律,预测的准确性仍需进一步提高。利用神经网络方法学习海量轨迹数据中隐含的时空规律知识,可提高候车时长建模的准确性[17]。
基于以上分析,本文提出利用作息时空特征改进神经网络的出租车乘客候车时长预测方法。本文以精细时空网格为单位,对城市兴趣点、出租车轨迹数据和时间作息片段等多源数据进行融合,并利用作息时空特征优化神经网络对出租车运载的时空规律进行建模,从而预测一定时空约束条件下的出租车乘客候车时长。本文方法的研究思路如图1 所示。
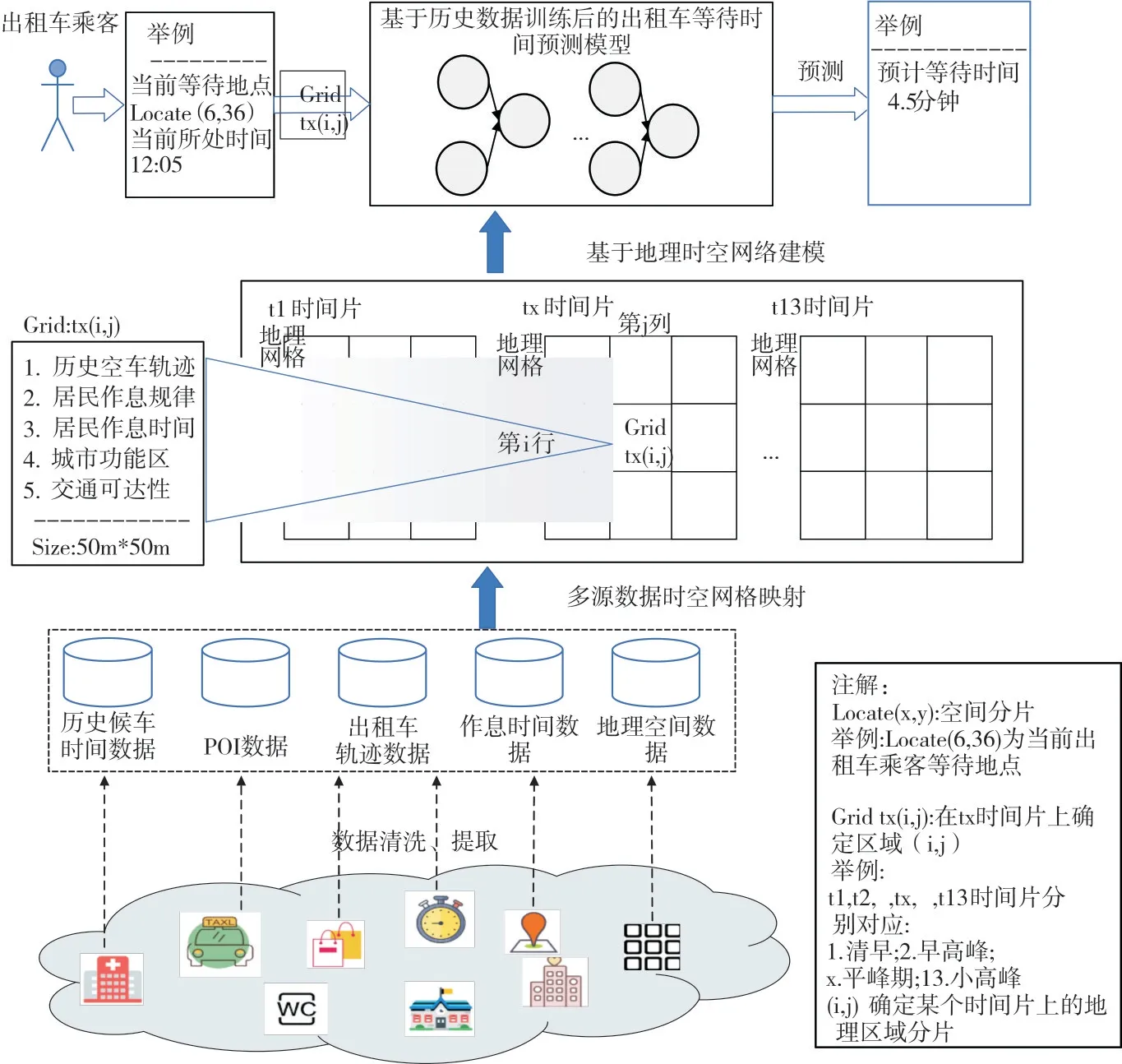
Fig.1 Research thoughts图1 研究思路
1 城市居民的作息时空特征分析
1.1 出租车轨迹数据分析
出租车GPS 数据包括数据ID、记录时间、地理位置(经度和纬度)、行驶速度、行驶朝向、载客情况等信息。大量精度高、覆盖面积广和内容丰富的出租车轨迹数据成为研究城市居民出行规律的重要数据来源[18-19]。常见的关键出租车轨迹数据结构如表1 所示。

Table 1 GPS taxi trajectory data structure表1 GPS 出租车轨迹数据结构
表2 为常见出租车轨迹数据中的数据片段。其中,T_Status 表示出租车载客状态标记,T_Status 为262 144 表示出租车为载客状态,T_Status 为0 表示该时刻出租车为空驶状态。

Table 2 Taxi trajectory data fragments表2 出租车轨迹数据片段
1.2 城市居民作息规律分析
出租车作为城市公共交通的重要参与者,在生活、工作与出行等方面扮演越来越重要的角色,是维持城市交通正常运行的重要螺丝钉。城市居民的作息时间、城市功能区域分类都反映出租车行车规律在城市中不断变化的灵活性、动态性[20]。
作息时空规律描述了城市居民生活、工作、学习和活动等各方面的时间空间特点,它是受城市生活习惯、人文环境、自然地理条件和社会经济水平等影响而形成的社会性特征。城市中的生活主体主要由国家公务员、专业技术人员、商务管理人员、个体营业者、上班族、学生、工人、退休人员和其他职业者组成[21-22]。由于居民工作日、节假日(包括周末和法定节假日)和乘车点的功能区类别是影响出租车乘客候车时长的主要因素[23-24]。因此,本文将轨迹数据记录根据时间标记为工作日和节假日两类,以区分不同时间特征片段的数据差异。同时,根据出租车所在城市网格的功能区属性标识数据记录的空间特征,以便为神经网络模型提供空间规律的学习依据。
1.3 城市居民作息时间特征提取
节假日城市居民的作息时空特征与在工作日时有明显区别。清晨05:00—08:59,城市居民大多处于休息状态,仅小部分居民有出行等活动;09:00—13:59 大部分居民陆续有外出活动,是节假日一天中的早高峰;14:00—17:59,居民一般会有就餐和逛街等活动需求;18:00—23:59 时间段是节假日一天中居民活动最频繁的晚高峰时期,包括夜晚用餐、出行及返家等出行活动;24:00—04:59,属于午夜时间段,居民一般处于睡眠状态。如表3 所示,将节假日一天24 小时按照城市居民的作息时空特征划分为5个时间片段并记上不同的标签。
工作日是劳动者在法定限度内应当从事劳动或者工作的时间,是工作时间的基本形式。一般在工作日中,务工人员和学生的作息时空特征具有相似性和重合性。工作日中,将夜晚分为上半夜和下半夜,上半夜为23:00—03:59,此时城市居民基本都处于睡眠状态;下半夜为04:00—06:59,此时一些个体营业者如早餐店经营者、环卫工人等已经开始工作。07:00—08:59 是城市居民一天中出行的第一个高峰期,称为早高峰,在此期间,学生和上班族都需外出上学或上班。09:00—11:59 为学生在校学习时间段,也是绝大部分上班族和其他职业者的工作时间,居民的出行活动在该时间段中趋于稳定。12:00—14:29 为午休时间段,人们有出行就餐或者短时间回家等活动,城市居民处于出行的小高峰。14:30—17:30 是下午上学和上班时间段。17:31—20:59,学生放学、上班族下班或者逛街购物等外出活动,是一天中的第二个高峰期,称为晚高峰。21:00—22:59 时间段内,居民一般会结束晚间活动回家休息。如表4 所示,将工作日中一天24 小时按照城市居民作息时空特征划分8 个时间片段。

Table 3 Holiday time sliced data set表3 节假日时间分片数据集
1.4 城市功能区特征提取
本文采用的高德城市PO(IPoint of Interest)数据包含了公司、购物、教育、商业住宅、风景、餐饮、公共设施、交通设施、生活、体育、医疗、政府和住宿等共计14 张表格。基于该数据,本文进一步将POI 细分为餐饮服务、公共设施、购物服务、商务住宅、生活服务、体育休闲服务、风景名胜、科教文化服务、私人诊所与专科医院、住宿服务、政府机构及社会团体、公司企业、ATM 与银行、停车场、大型商圈、大型医院、大型场馆和公交车站等19 种类别。由于一些体育馆、科技馆、少年宫等大型场馆、大型商圈、景区和综合医院的活动规律对节假日和工作日的依赖程度较大,将景区、大型场馆、大型商圈和综合医院归纳为特殊功能区类。最终形成的兴趣点类别如表5 所示。功能区类型数据结构如表6 所示。

Table 4 Workday time sliced data set表4 工作日时间分片数据集

Table 5 Urban functional areas category data set表5 城市功能区类别数据

Table 6 Time slice data structure表6 功能区类型数据结构
考虑到同一个地理网格可能存在多个功能区属性,本文通过综合经济引力、交通可达性和金融联系网络3 个维度,基于城市间经济流、人流和物流、资本(金融)流等要素相互作用的强度,确定每类功能区主导地位权重[25]。根据单位网格中主导地位权重高低,确定网格功能区类别为其最高级别的优先级。
2 基于作息时空特征优化的神经网络模型
2.1 多源数据融合
以不破坏房屋和道路结构为前提,综合考虑城市规划布局、地理地形和资源配置等影响出租车乘客候车时间的因素,将完整的行政地图按照规定大小的单位矩阵划分为若干个矩阵,即地图网格[26]。地图网格细节如图2 所示。

Fig.2 Mapping gridding图2 地图网格化
地图网格数据信息包括网格序号和网格中心点坐标(经度和纬度)。基于单位网格大小和网格中心点坐标,根据经纬度和米的换算公式得出:
经度(东西方向)1m 的实际度:

纬度(南北方向)1m 的实际度:

根据式(1)、式(2)可以计算得到网格中经度的最小值、最大值和纬度的最小值、最大值,分别记为Longi⁃tude_min、Longitude_max、Latitude_min 和Latitude_max。本文地图匹配采用点到线匹配的九宫格网格,这是一种基于普通网格算法扩展的匹配算法。在设计网格大小时,主要考虑到打车点周围环境因素对空载出租车停车的影响,即在大多数情况下,50m*50m 范围内的环境因素较为一致,而超过该范围,容易出现不同的停车周边环境,可能影响到空车停车的决策。如,红绿灯附近,出租车无法停靠;公交车站周围30m 内,出租车无法停车等。鉴于此,本文九宫格由9 个边长为50m 的正方形组成。每个网格所在的值都已在图中标识出来,如图3 所示。
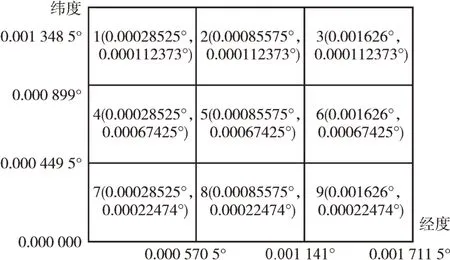
Fig.3 Nine-grid geographic information图3 九宫格网格地理信息
地图网格信息表格式及含义如表7 所示。fishnet_id 表示网格id,POINT_X 表示网格中心的x坐标,POINT_Y 表示网格中心的y坐标。

Table 7 Map grid information data表7 地图网格信息数据
地图网格信息表中的数据片段如表8 所示。

Table 8 Map grid information data fragment表8 地图网格信息表数据片段
根据出租车轨迹数据中记录的GPS 定位信息(经度、纬度)与地理网格信息对比匹配,寻找出租车轨迹点所属网格号。此外,根据轨迹数据中的时间点和日期,对照节假日和工作日不同的时间片段分类,标记所属时间片段。最后,通过行政地图网格化的操作实现出租车连续轨迹离散化,将候车时间数据、POI 数据、出租车轨迹数据、作息时间数据和地理空间数据,根据时间和空间数据匹配对比后映射至每个网格中,使得每个单位网格都包含融合的多源数据。多源数据融合后的轨迹数据片段如图4 所示。

Fig.4 Data fragment of multi-source data fusion图4 多源数据融合的数据片段
2.2 利用作息时空特征优化神经网络模型
由上文可知,根据出租车轨迹数据中空驶状态(T_Sta⁃tus 为0)出租车出现在该网格中的记录时间(T_UTCTime),根据式(3),可计算出租车乘客的候车时长。

根据之前分析的作息规律,结合网格区域特征,历史轨迹数据被划分为若干个时空片段,每一个轨迹时空片段即为该时间段中该区域网格的轨迹数据,这些时空片段作为神经网络模型的训练数据[27-28],式(3)中的候车时长表示单位网格中乘客的候车时间。
靳蕃[29]提出:只要有一个隐藏层的三层BP 神经网络,就可以无限接近任何映射函数并完成给定的映射任务。本文比较不同隐藏层的层数分别为1、2、3、4 时,作息时空特征约束神经网络模型结果。
由表9 可知,当隐藏层节点数为3 时,模型精度最高。因此,本文模型基于一个五层结构的全连接网络的神经网络建立相关模型,对乘客候车时长进行预测。模型拓扑结构如图5 所示。

Table 9 Error table for different hidden level表9 隐藏节层数对应误差
多方位分析影响出租车上下车点变化的因素,便于从出租车轨迹数据中发现规律、归纳特征,从而为本文在构建算法模型时提取实际影响乘客候车时长的元素,并为乘客推荐候车点提供科学合理的决策依据。
本文神经网络模型的特征输入值选取了4 个主要影响该网格内出租车乘客候车时长的因素,分别标记为:X1是基于城市居民作息特征的所属时间片段,X2是基于POI 数据划分的城市功能区类别,X3标记该天是否是节假日,X4是判断该网格是否处于大型商圈、大型场馆和综合医院等特殊地点。输出层为唯一神经元输出Y,表示乘客在网格中等待第一辆空驶出租车所需要的时间。由于Relu 函数分段线性的特征,该函数的负值都为0,而正值不发生改变,即单侧抑制。使得神经网络中的神经元也具有了稀疏激活性,更容易学习优化。对于非线性函数而言,Relu 函数由于非负区间的梯度为常数的特性,克服了梯度消失问题(Vanishing Gradient Problem),使得模型收敛速度维持在一个稳定状态。Relu 函数公式如式(4)所示,Relu 函数的图像如图6 所示。
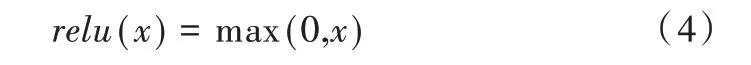
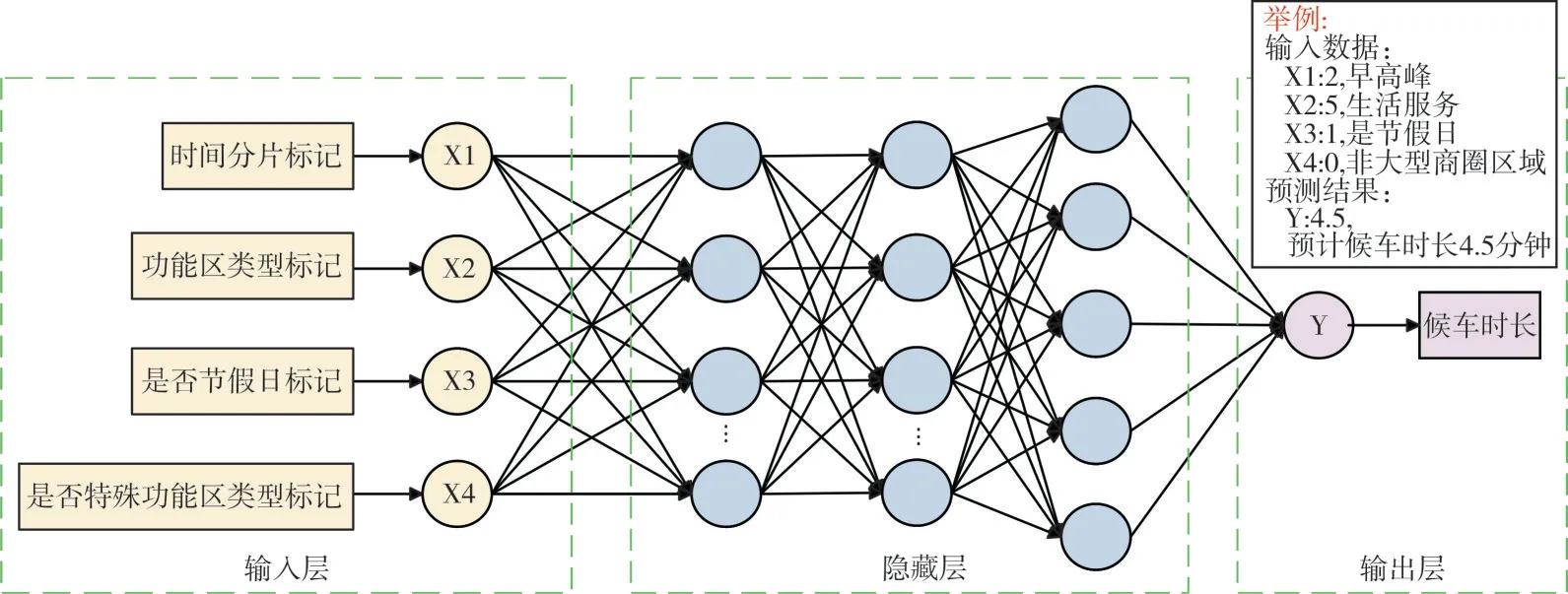
Fig.5 Topological structure of neural network图5 神经网络拓扑结构

Fig.6 Relu activation function diagram图6 Relu 激活函数图像
自适应性矩估计(Adaptive Moment Estimation,Adam)的基础是训练数据迭代更新神经网络权重的一阶优化算法,结合了自适应梯度算法和均方根传播算法最优的性能,它还是能提供解决稀疏梯度和噪声问题的优化方法,可以替代传统随机梯度下降(Stochastic Gradient Descent,SGD)算法。其核心是初始化偏差修正项,偏差修正项可基于一阶矩估计和二阶矩估计推导,更适合解决本文这类大规模数据问题。本文模型使用自适应学习率优化算法Ad⁃am 对网络参数进行更新。
3 基于优化神经网络的出租车乘客候车时间预测
本文针对为出租车乘客推荐候车点的问题,基于大量融合后时空轨迹数据的时空特性,提出一种候车点推荐算法。详细分析居民作息时间规律特征和城市功能区的类型特征,提出影响候车时长的主要因素;通过对时间特征标记获取工作日或节假日等信息,通过定位数据结合POI标记乘客所处地点的功能区类型,判断是否处于大型场馆、商圈或者综合医院。乘客所处的动态时空环境信息直接影响着出租车运载规律。本文模型预测流程如下:
步骤1:将网络初始化,输入特征值归一化处理,如式(5)所示。
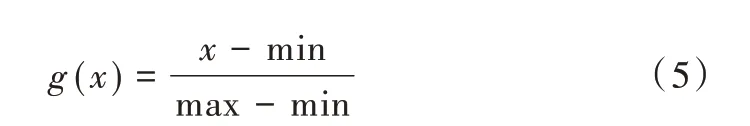
步骤2:神经网络正向传播,计算预测结果。式(6)、式(7)分别为隐藏层和输出层的输出公式。Xi为输入层的值,Wij和Wjk是隐藏层和输出层对应神经元的权值矩阵,b为神经元的偏置。
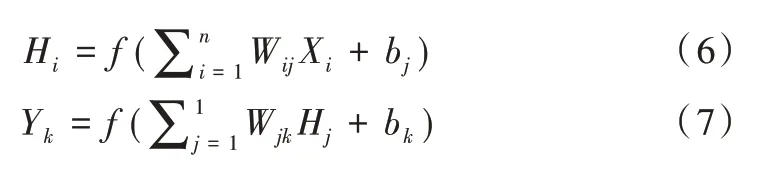
(fx)函数为Relu 激活函数,如式(8)所示。

步骤3:利用梯度下降计算每一个神经元的损失。权值和偏置损失如式(9)、式(10)所示。
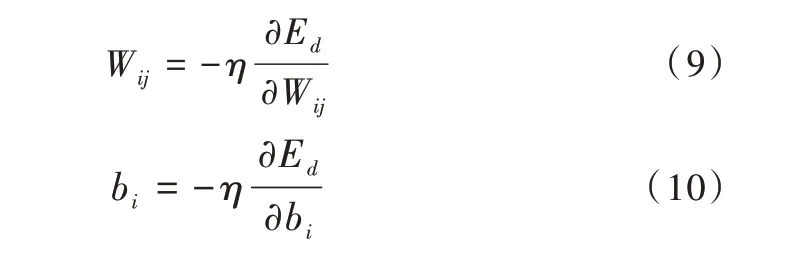
其中,Ed为损失函数,如式(11)所示,y 表示神经网络的预测值,y_表示实际值,η 为学习率。
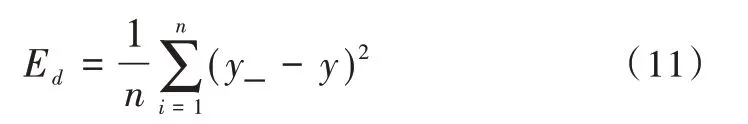
步骤4:神经网络反向传播误差信息,更新每个神经元的权值和偏置,如式(12)和式(13)所示。

基于优化神经网络的出租车乘客候车时间预测流程如图7 所示。
本文动态计算模型主要步骤包括:①将用户提交的时间、空间信息,转换为时间分片数据、节假日工作日类型数据、城市功能类型数据和是否特殊地点数据;②将步骤①的4 种数据标记为模型输入特征值;③若用户的时间空间信息发生变化,则需要重复步骤①、步骤②;④根据输入特征值模型得到计算结果,即乘客的预测候车时长。
基于优化神经网络的出租车乘客候车时间预测算法伪代码如下:
预测模型算法
input:乘客时间信息Tu,乘客空间地理信息Su
output:乘客候车时长Lu
1.初始化定期更新时间“T”
2.for(每隔时间T)
3.while(Tuor Su发生改变)
4.计算根据Tu和Su信息,得到该网格中乘客时长Lu
5.end for
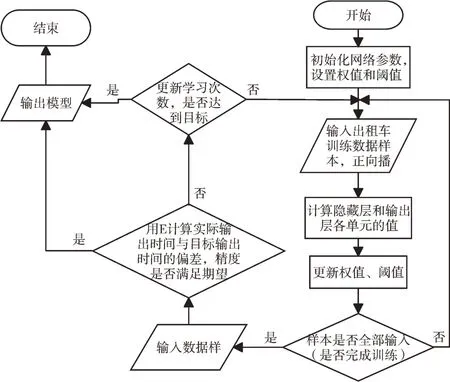
Fig.7 Work and rest spatio-temporal feature optimization neural network flow图7 作息时空特征优化神经网络流程
4 实验设计与结果分析
4.1 实验环境与数据描述
本文实验的硬件环境是Inte(lR)Core(TM),i7-8550U CPU@ 1.80HZ,Windows 10,8G 内存;软件环境为Py⁃thon3.5,TensorFlow1.7.0 和Keras 框架。
实验选取2014 年2 月13 日至2014 年2 月19 日湖北省武汉市武昌区的出租车轨迹数据,经过异常数据清洗剔除后得到出租车轨迹数据共6 705 086 条,该时间段内涵盖工作日、节假日和特殊节日(情人节),数据具有典型代表性且稳定。
武昌区地理位置为东经114°14'~114°30',北纬30°32'~30°37',按照50m*50m 单位使用ArcGIS 10.3 一共划分了84 048 个网格。武昌区内共有POI 数据34 195 条,作息特征网格化后轨迹数据共有6 705 086 条,选择其中5 705 086条数据作为训练数据,1 000 000 条数据作为测试数据。实验针对处在不同时间片段和功能区的出租车进行预测,由于平均绝对误差(Mean Absolute Error,MAE)直观反映实验预测结果与实际值的偏离程度,因此选用MAE 对实验结果进行评估,如式(14)所示。
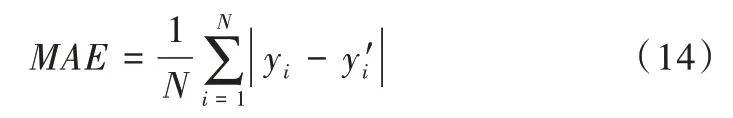
式(14)中,N 表示实验结果个数;yi表示出租车乘客的候车时长;yi' 表示乘客等到第一辆空车的预测时间。
4.2 时间特征对预测模型的影响
根据表4 将工作日中连续的24 个小时划分为8 个时间片段;表3 将节假日中连续的24 个小时划分为5 个时间片段。系统对工作日和节假日中出租车乘客等待时间进行预测,根据实验结果和预测结果计算不同时间片段的平均绝对值结果如图8 所示。
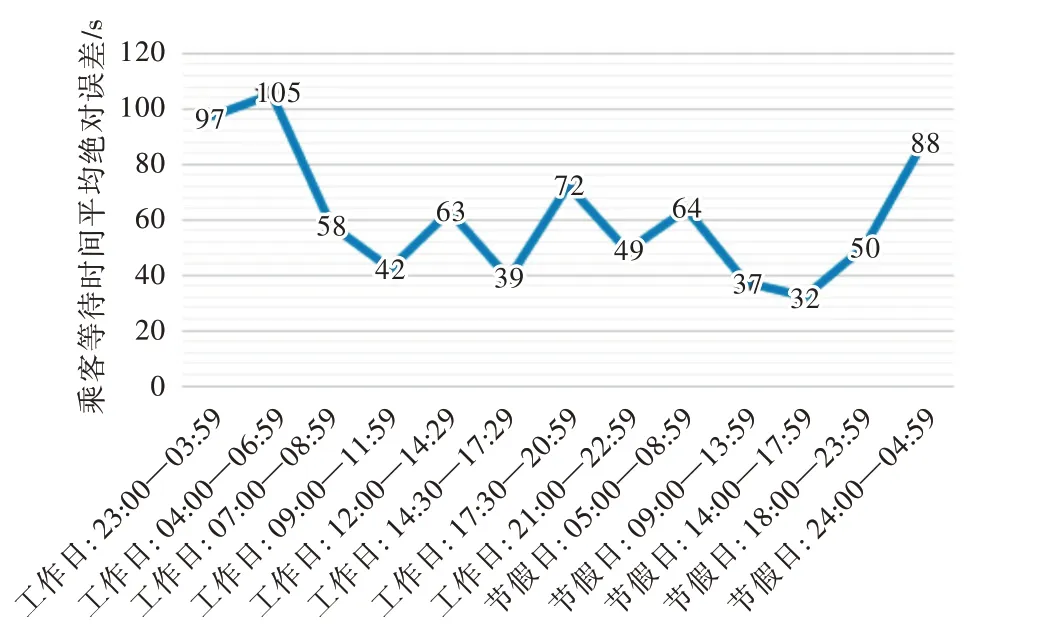
Fig.8 Prediction effect of different time segments图8 不同时间片段的预测效果
图8 中,不同时间片段预测得出的MAE 值在一定范围内,最差效果的MAE 值为105s,即乘客在任意时间片段等待第一辆空驶出租车的时间预测平均误差不超过2min,误差范围属于理想范围[30]。因此,出租车乘客在不同时间片段内都可通过本文算法模型预测出比较准确的出租车乘客候车时长。
4.3 空间特征对预测模型的影响
根据上文将城市功能区划分为19 种类别。本文模型针对所处不同功能区类别的乘客等待时间进行预测,按照分类其平均绝对误差如图9 所示。

Fig.9 Prediction effect of different functional areas图9 不同功能区的预测效果
由图9 可以看出,不同功能区的预测MAE 值在一定范围内,最差效果的MAE 值为116s,即乘客在任意功能区等待第一辆空驶出租车的时间预测平均误差不超过2min,说明通过本文算法模型可以计算出误差较小的出租车乘客候车时长。
乘客在不同功能区内等待出租车都可通过该模型预测出误差较小的候车时长。即模型不考虑空间特征因素对预测结果的影响时,模型的预测结果与原始模型的预测结果相比,准确率降低。由此可得,时间和空间因素影响出租车乘客候车时长。
4.4 不同模型结果比较
原始未优化的三层BP 神经网络算法模型属于一种“有教师学习的”的多层前馈网络,采用误差逆传播进行网络训练,本质上是在训练过程中寻求误差最小化并对网络连接权值进行调整与优化,从而对乘客候车时长进行预测。文献[13]中提出的基于经验分布预测等待时间的算法模型适用于经验分布,模型简单、计算量少,适用于大数据处理,通过修复后的大量GPS 数据进行基于经验分布模型统计和计算后得到乘客候车时长。上述两种算法模型均未充分挖掘出出租车的行驶规律,候车时长的预测准确性有待提高。
通过使用本文提出的算法模型、原始未优化的三层BP神经网络算法模型和文献[13]中提出的基于经验分布预测等待时间的算法模型,分别记为SF1、SF2 和SF3。实验数据统一为6 705 086 条,为了提高实验结果的可信度,添加准确率作为评价指标之一。
其中,wt表示真实值,wp表示模型预测值,acc表示模型预测结果准确率。算法模型的MAE 值和准确率如图10 所示。
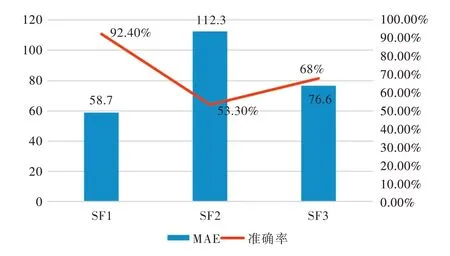
Fig.10 Experimental result graphs of different algorithm models图10 不同算法模型实验结果
由图10 可知,本文提出的作息时空特征优化神经网络算法模型即SF1,MAE 值为58.7,其准确率为92.4%;原始未优化的三层BP 神经网络算法模型即SF2,MAE 值为112.3,该模型的准确率为58.3%;文献[13]中模型即SF3,MAE 结果为76.6,准确率为68%。
根据模型预测结果比较可知,本文提出利用作息时间特征优化神经网络的出租车候车时长预测模型能够提高预测出租车乘客候车时长的准确率,减小误差。
4.5 实际场景运用
为了直观展示本文模型的作用,基于作息时空特征优化神经网络模型,开发了出租车打车决策原型APP。如图11 所示,某乘客在此时所处位置选择打车,预计需要等待4.5min 才会有第一辆空驶出租车经过。在一定半径范围内,原型APP 还根据预测的候车时间长度进行长度倒排序,优先为用户推荐等待时长最短的乘车点。

Fig.11 Application effect of waiting time model in mobile APP图11 等待时间模型在手机APP 中的应用效果
5 结语
影响出租车乘客候车时间的因素有很多,比如城市交通发展战略、出租车运营利润和城市交通基础设施等因素,都会对乘客候车时长产生影响。结合轨迹数据和城市居民的作息时空规律,通过比较分析改进神经网络建模的预测结果与实际数据,证明了本文模型的适用性、准确性和有效性。本文模型有助于确保空驶出租车与乘客之间的供需一致性,帮助乘客提前预判候车时长,极大提高了打车成功率,促进城市居民的智慧出行。然而,本文模型仅考虑到时间和空间因素对打车的影响,后续研究将进一步展开空气质量和天气状态等因素对出租车候车等待时长的影响。

