负泊松比材料于可重构天线反射面的应用研究
徐 斌 张华振 侯仰青 江水东 兰 澜
负泊松比材料于可重构天线反射面的应用研究
徐 斌张华振侯仰青江水东兰 澜
(1. 中国空间技术研究院西安分院,西安 710000;2. 上海跃盛信息技术有限公司,上海 200240)
为了提高在轨卫星天线反射面型面重构过程中的变形能力,减小局部应力及作动力,提高型面重构的精度,对反射面重构中的变形情况进行力学理论分析,得到泊松比参数对型面重构应力的影响。本文给出了反射面在主曲率方向的曲率变化及面内应变变化情况下,使应力最小的泊松比参数取值方法。以一可重构赋形反射面为算例,采用具有阵列椭圆孔结构的泊松比可设计超材料作为发射面材料,通过优化椭圆孔的几何参数,得到所需泊松比参数;以提高型面重构精度及作动力小为目标,通过有限元仿真计算确定反射面的厚度。
机械式可重构反射面(MRR);负泊松比;超材料
1 引言
在卫星通信系统中,传统的赋形天线只有一个固定的反射面几何,只能提供特定的辐射场型及固定的目标增益区。机械可重构反射面(MRR)的天线可以通过重构反射面调整其辐射场型图,实现卫星天线的波束形状的在轨重构,覆盖服务区的赋形波束能够随通信需求的变化而变化。因此,空间可重构天线使用寿命内覆盖多个不同的区域,可以减少天线数量,节约发射成本。
在过去的几十年中,有大量关于机械式可重构反射面的研究。其中,P. J. B. Clarricoats研究了一种底部分布了多个作动器的金属经编织网反射面,根据他的研究,要得到光滑的重构型面,反射面材料的弯曲刚度与杨氏模量的比值(D/E)须尽可能大。
Leri Datashvili 等人以柔性纤维复合材料设计了一种可变形反射面,通过在表面层填充硅颗粒,使其同时具有很好的力学性能和射频性能。
邵恕宝等采用三明治结构来制备反射面,包含三层:顶层及底层为BWF CFRS,中间层为铝蜂窝。其结构简单,并可弹性调节弯曲刚度与杨氏模量的比例系数(D/E)。
以往对可重构曲面力学性能的研究主要集中在拉伸模量、剪切模量和弯曲刚度方面。由于泊松比参数对于某一确定材料是不可改变的,且多为正值,所以研究者们对泊松比参数对型面变形的影响研究很少。近年来,具有任意复杂微结构的所谓“设计材料”越来越引起人们对超材料概念的关注。通过对微结构的合理设计,超材料在宏观尺度上可表现出不同的力学性能,如泊松比参数的设计,包括负泊松比(negative Poisson’s ratio, NPR)。
本文通过对反射面型面大变形下的应力进行理论研究,得出应力与泊松比参数之间的关系,得到更优的泊松比参数,并在此基础上优化反射面材料单元的结构参数,使反射面变形时的应力较小,同时得到较高的型面精度。
2 反射面重构变形的力学分析
反射面的重构通过面下多个作动器的驱动实现。通过曲率变化和面内应变的结合,实现了由原始形状产生弹性面外变形。应力由弯曲应力()及面内应力()两部分组成。根据弹性力学理论,式(1)可用来计算在,方向的应力及剪切应力。


2.1 纯弯曲变形的应力分析
对于赋形反射面,在型面上不同位置的作动器作用下,曲率K和K的变化是不同的。在弯曲变形起主导,面内应力忽略的情况下,假定和方向为主曲率方向,主应力分别为σ和σ。在和方向的弯曲应变可以通过曲率的变化值及型面厚度按式(2)计算:

将式(2)代入式(1)得到、方向的应力分量:
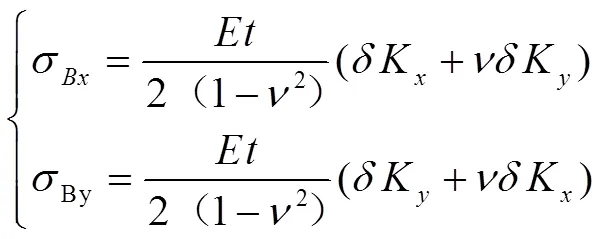

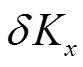

最大弯曲主应力大小为:



通过对式(7)求导,可得到最小弯曲应力下的泊松比参数取值:


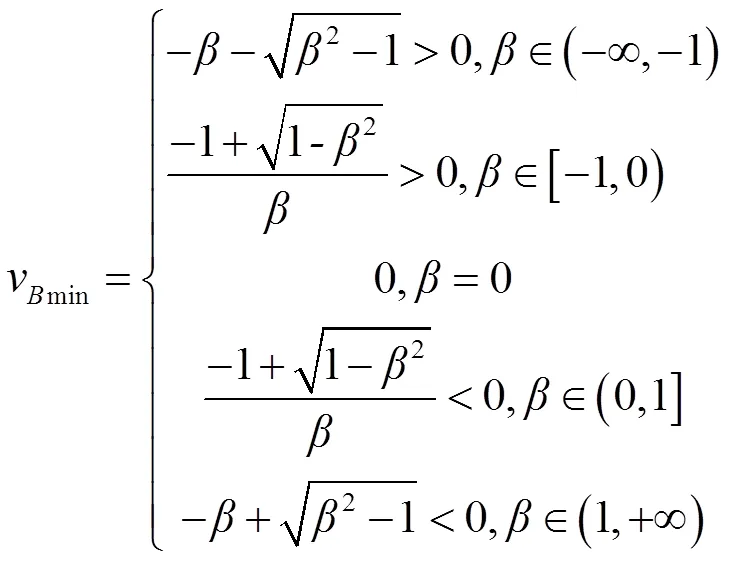
综合以上分析可以看出,当<0,即、曲率变化符号相反(×<0),ν为正;当>0,即、曲率变化符号相同(×>0),ν为负;当=0,即、曲率变化至少有一个为零时,ν为零。为了证实以上结论,分别取-1、-0.5、0、-0.5、1,绘制弯曲应力关于泊松比参数的曲线,如图1所示。ν分别为1、0.265、0、-0.265、-1。当=1,弯曲应力在随着泊松比参数增大而增大,当=-1,弯曲应力随泊松比增大而减小。

图1 弯曲应力vs泊松比参数曲线
2.2 面内变形的应力分析
根据弹性力学理论,、方向的面内应力如下:

在仅考虑面内变形的情况下,则主应力为:

与上节中弯曲应力与泊松比关系进行相同方法的分析,得到相似的结论,即:当应变符号相反(ε/ε<0),泊松比对应于最小主应力的取ν为正值;当应变符号相反(ε/ε>0),ν为负值;当ε、ε之一为零,ν=0。
2.3 综合面内及弯曲变形的反射面变形应力分析
在作动器作用下的反射面表面变形包括了弯曲及面内的变形。在及方向的总应变可将面内应变及弯曲应变叠加如下:

联立式(1)、式(2)、式(12),在及方向的应力表示为:
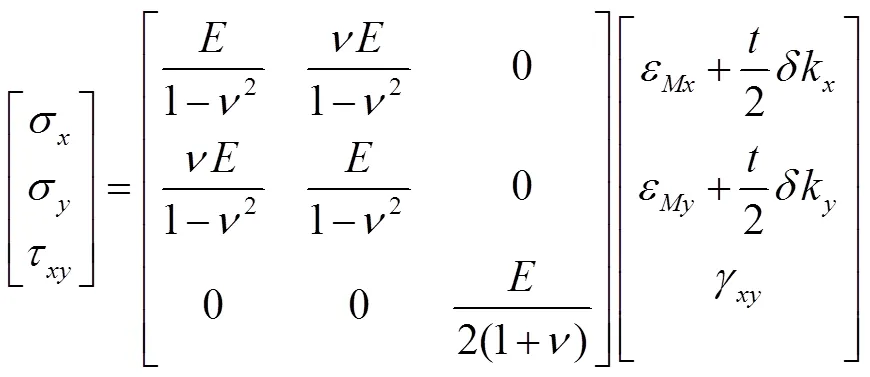

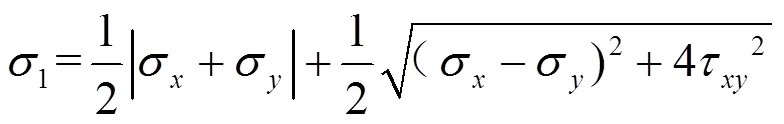
本文以一可重构赋形反射面为例进行研究。该反射面有两个不同的工作型面,覆盖两个不同的区域,如图2a所示。应用Matlab计算在型面重构变形中相同、坐标下的坐标变化值,得到型面上的位移如图2b。型面变形后,、方向的曲率变化及高斯曲率变化可由式(15)计算,通过应用Matlab软件得到曲率变化图,如图3所示。


点处的面内应变可以通过中性面节点的几何变形进行计算。如图4所示,、分别为初始型面和目型面中性面上的对应节点,、为在方向与、相邻的节点,、为在方向上相邻的点,应变由式(16)计算:

(16)

图5 应变计算结果
应用Matlab计算面内应变及剪切应变,结果如图5所示。在点处的、方向面内应变为0.022、-0.005,剪切应变为0.017。


图6 应力与泊松比参数的曲线
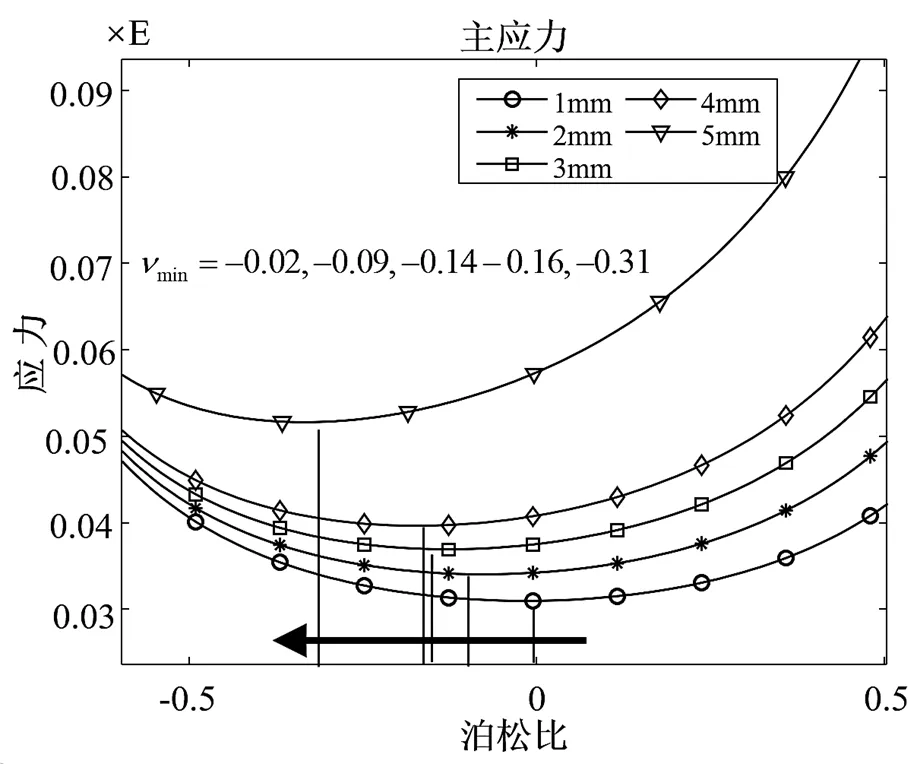
图7 主应力与泊松比参数曲线
4 反射面优化设计
4.1 点阵结构材料
根据图7计算结果,当反射面厚度大于1mm,对应于最小应力的泊松比参数为负值。传统的蜂窝结构材料常用来制备反射面,但泊松比多为正值。Bertoldi等人提出了一种具有负泊松比参数的阵列椭圆孔点阵材料,如图8所示。该二维结构由椭圆孔按周期排列形成阵列,其中椭圆孔有水平及竖直两个方向,且相邻椭圆孔的方向不同,所以在水平和竖直两个方向上的弹性力学参数是相同的。等效的泊松比参数可通过调整椭圆孔的几何参数、及设计。

图8 阵列椭圆孔负泊松比材料
考虑到穿透损失,孔径需小于电磁波的波长的1/8。本文反射面应用于X波段,波长为30 mm,则椭圆孔的几何参数取值为3.65 mm。为降低面内拉伸刚度,可以减小几何参数,但同时可能增加其加工难度,由于太小,在加工中容易相邻椭圆孔之间的“脖子”处容易断裂。综合考虑,取为0.3 mm。通过有限元仿真,如图9所示,计算出不同椭圆率下,阵列椭圆孔材料的等效泊松比ν如下:


图10 等效泊松比关于椭圆率b/a曲线
反射面材料采用碳纤维增强硅胶,其杨氏模量E为500MPa,泊松比为0.4。仿真计算结果如图10所示,等效泊松比ν随着椭圆率/单调增大。
4.2 反射面厚度优化
反射面厚度是面外变形的一个重要影响因素。从式(18)可以看出,弯曲刚度是厚度的三次方关系。根据文献[4]所述,在面外弯曲变形中,为使变形后型面光滑,弯曲刚度与杨氏模量的比值(/)须足够大,而增加厚度是增加弯曲刚度的有效方法,但将使局部的曲率变化小,而使总体的变形增大。

为优化厚度,对几个厚度值分别为1mm、2mm、3mm、4mm、5mm的反射面进行仿真计算:

表1 阵列椭圆孔的几何参数

ANSYS用来计算不同厚度的反射面在225个作动器驱动下的型面变形。作动器布置在局部区域高斯曲率极值点上。图11所示为其中一个反射面在作动器下的变形结果。型面的精度以型面与目标型面的均方根误差(RMS)来评价,计算如式(19):
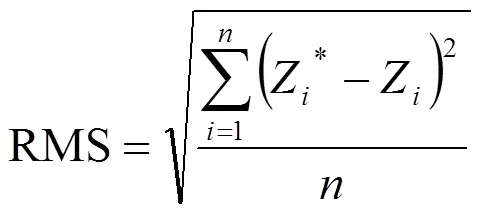
其中,Zi*为仿真结果型面的z坐标,Zi为目标型面上相同x、y坐标对应节点的z轴坐标。

图12 不同厚度仿真型面的RMS误差分布
在本文的案例中,不同厚度反射面RMS计算结果如图12所示,当厚度从0.5mm增大到5mm时,RMS递减,型面的精度升高,当厚度大于5mm后,RMS开始增加,如图12e所示。变形所需的作动力也相应地随厚度增大,意味着反射面和作动器的质量增大,提高火箭发射成本。所以,在满足精度的条件下,选择小的厚度。
5 结束语
泊松比参数是影响反射面变形应力的重要力学参数,通过弹性力学理论分析,反射面的重构变形包含了面内变形及弯曲变形(曲率变化)。对应于应力最小的泊松比参数需根据型面厚度,及主曲率方向上的曲率变化和面内应变情况取值,即:当两个主曲率变化方向相同(δK×δK>0),泊松比取负值得到最小的弯曲应力;相反地,泊松比取正;若其中一个曲率变化为零(δK×δK=0),泊松比取值为零时,弯曲应力最小。同样地,对于面内应力,当δεδε>0,泊松比参数取为负;δεδε<0,泊松比参数取为正;δεδε=0,泊松比参数取为零。而对于主应力,是弯曲应力和面内应力的叠加,但厚度较小时,弯曲应力较小,主应力取得最小值的泊松比接近,随着厚度增加,弯曲应力增大,主应力取得最小值的泊松比将向靠近。
通过实例分析,本文采用阵列椭圆孔超材料制作反射面,通过优化设计椭圆孔的几何参数实现变泊松比调整,根据型面重构精度优化设计反射面的厚度。
1 Clarricoats P, Hai Z, Brown R C, et al. A reconfigurable mesh reflector antenna[C]. The 6th International Conference on Antennas and Propagation, university of warwick, UK, April 4-7,1989
2 Clarricoats P, Zhou H. Design and performance of a reconfigurable mesh reflector antenna. I - Antenna design. II - Antenna performance[J]. Microwaves, Antennas and Propagation, IEE Proceedings H, 1991, 138: 485~496
3 Clarricoats P, Zhou H. The design and performance of a reconfigurable mesh reflector antenna[C]. International Conference on Antennas & Propagation, University of York, UK, April 15-18,1991
4 Brown R C, Clarricoats P, Hai Z. The Performance of a Prototype ReconfigurableMesh Reflector for Spacecraft Antenna Applications[C]. The19th European Microwave Conference, London, UK, October 4-6,1989
5 Pontoppidan K, Boisset J P, Crone G. Reconfigurable reflector technology[C]. IEE Colloquium on Satellite Antenna Technology in the 21st Century, London, Jun 12, 1991
6 Pontoppidan K. Light-Weight Reconformable Reflector Antenna Dish[C]. Proceedings of 28th ESA Antenna Workshop on Space Antenna Systems and Technologies, Noordwijk, The Netherlands, May 31- June 3, 2005
7 Rodrigues G, Angevain J C, Santiago-Prowald J. Shape control of reconfigurable antenna reflector: Concepts and strategies[C].The 8th European Conference on Antennas and Propagation, Hague, The Netherlands, April 4-11, 2014
8 Rodrigues G, Angevain J C, Santiago-Prowald J. Shape optimization of reconfigurable antenna reflectors[J]. Ceas Space Journal, 2013, 5(3-4): 221~232
9 Sakamoto H, Tanaka H, Ishimura K, et al. Shape-Control Experiment of Space Reconfigurable Reflector Using Antenna Reception Power[C].3rd AIAA Spacecraft Structures Conference, California, USA, January 4-6,2016
10 Tanaka H, Natori M C. Study on a Reconfigurable Antenna System Consistingof Cable Networks[J]. Transactions of the Japan Society for Aeronautical& Space Sciences, 2007, 50(167): 48~55
11 Susheel C K, Kumar R, Chauhan V S. An investigation into shape andvibration control of space antenna reflectors[J]. Smart Materials & Structures,2016, 25(12):125018
12 Viskum H H, Clarricoats P, Crone G. Coverage flexibility by means of aReconformable subreflector[C]. Antennas and Propagation Society InternationalSymposium, Montreal, Canada,July 13-18,1997
13 Washington G, Yoon H S, Angelino M, et al. Design, modeling, and optimizationof mechanicallyreconfigurable aperture antennas[J]. IEEE Transactions onAntennas & Propagation, 2002, 50(5): 628~637
14 Cappellin, Cecilia, Pontoppidan, et al. Feasibility study and sensitivity analysisfor a reconfigurable dual reflector antenna[C]. European Conference onAntennas & Propagation. IEEE, Berlin, Germany, 2009
15 Datashvili L, Baier H, Wei B, et al. Mechanical Investigations of in-Space-ReconfigurableReflecting Surfaces. Proceedings. of ESA Antanna workshop,Noordwijk, The Netherlands October 2010
16 Datashvili L S, Baier H, Wei B, et al. Design of a MorphingSkin Using FlexibleFiber Composites for Space-Reconfigurable Reflectors[C]. iaa/asme/asce/ahs/asc Structures, Structural Dynamics & Materials Conference. Boston, USA,2013
17 Shubao S, Siyang S, Minglong X, et al. Mechanically reconfigurable reflectorfor future smart space antenna application[J]. Smart Material and Structure,2018, 27(9):095014
18 Kolken H M A, Zadpoor A A. Auxetic mechanical metamaterials[J]. RSCAdvances, 2017, 7(9): 5111~5129
19 Bertoldi K, Reis P M, Willshaw S, et al. Negative Poisson's Ratio BehaviorInduced by an Elastic Instability[J]. Advanced Materials, 2010, 22(3):361~366
20 Pozniak A A, Wojciechowski K W, Grima J N, et al. Planar auxeticity from elliptic inclusions[J]. Composites Part B Engineering, 2016, 94(Jun.): 379~388
Application Research on Negative Poisson’s Ratio Material for Reconfigurable Antenna Reflector
Xu BinZhang HuazhengHou YangqingJiang ShuidongLan Lan
(1. China Academy of Space Technology (Xi’an), Xi’an 710000; 2. Shanghai YS Information Technology Co., Ltd., Shanghai)
In order to improve the deformation ability of reconfigurable reflector, decrease the local stress and power, improve the precision of surface reshaping, the effect of Poisson’s ratio to the reflector reshaping is investigated through mechanical study of reconfigurable reflectors in this paper. A method of determining Poisson’s ratio parameter to minimize the stress of the reflector surface under the vary conditions of the curvature change and the membrane strain change in the main curvature direction is presented. A case of reconfigurable reflector is studied. A Poisson’s ratio designable metamaterial with structure of elliptic voids array is used for the reflector, and the required Poisson’s ratio parameters were obtained by optimizing the geometric parameters of the elliptical voids. In order to improve the reshaping precision of the surface and reduce the operating force, the thickness of the reflector surface was determined by finite element simulation.
mechanically reconfigurable reflector(MRR);negative Poisson’s ratio;metamaterial
TN82;TB3;O31
A
徐斌(1984),在读博士后,电子科学与技术专业;研究方向:可重构天线反射面材料。
2021-04-08


