基于改进的基因表达式编程自动优化CNN

龚道庆，彭昱忠,2+，邓楚燕，袁 程，曹爱清，李红亚

(1.南宁师范大学 计算机与信息工程学院，广西 南宁 530299； 2.复旦大学 计算机科学技术学院，上海 200433；3.广西民族大学 预科教育学院，广西 南宁 530006；4.许昌电气职业学院 信息工程系，河南 许昌 461000)

0 引 言

卷积神经网络(convolutional neural networks，CNN)具有良好的特征提取能力和泛化能力，在图像分类、自然语言处理和模式识别[1-3]等领域被广泛应用。Lecun等提出了基于梯度学习的卷积神经网络LetNet-5模型并将其应用于手写数字识别，该模型的成功应用引起了学术界的广泛关注；Krizhevsky等提出了AlexNet模型，它与LetNet-5模型相似，但其具有更多的网络层数，该模型在较大数据集Image Net[4]图像分类任务中获得最佳效果；随着AlexNet取得成功，科研人员在其基础上又提出了其它的完善方法，例如由微软研究院的何凯明等在文献[5]中提出的残差网络(residual neural network，ResNet)，通过使用Residual Unit成功训练152层卷积网络，在ILSCRC2015年比赛中以3.75%的top-5错误率，获得比赛冠军。另外，ResNet、NIN、GoogleNet、VGGNet、ZFNet、DenseNet、DPN和SENet也同样是具有代表性的模型。

卷积神经网络设计，大多需要经验丰富的专家来完成。网络优化本质上是一个受金钱、计算能力和时间约束的迭代过程，这将耗费大量人力物力资源。一些精确的优化算法(如基于梯度搜索算法)在解决神经网络优化问题时是无效的[6]。因此，研究人员提出了各种基于启发式计算范式的网络优化算法，如，随机搜索[7]、基于贝叶斯优化[8]、树状网络的Parzen估计量[9]、基于序贯模型的全局优化[10]、扩展拓扑的神经进化[11]、进化的无监督深度学习[12]等。

近年来，进化算法在神经网络优化问题上被证明为最具竞争力的方法[6]。基因表达式编程算法融合了遗传算法和遗传编程的优点，而多细胞基因表达式编程又具有更丰富的表达能力和搜索空间，因此本文提出利用模糊控制多细胞基因表达式编程(fuzzy control multi-cell gene expression programming algorithm，FMCGEP)算法来自动优化卷积神经网络的方法，并把该算法应用在多个图像分类数据集中，与经典算法和其它先进算法对比，本文提出的算法表现出更好的效果。

1 相关理论基础

本章节首先介绍了模糊控制多细胞基因表达式编程算法，然后对卷积网络基本原理进行概述。

1.1 模糊控制多细胞基因表达式编程

基因表达式编程算法(gene expression programming，GEP)继承了遗传编程(GP)的树形网络灵活多变与遗传算法(GA)的定长线性的特点。多细胞基因表达式编程(multi-cell gene expression programming algorithm，MCGEP)是在GEP的基础上引进了同源基因的概念，相对于普通GEP而言，MCGEP具有更丰富的表达能力和搜索空间。模糊控制多细胞基因表达式编程是在MCGEP基础上引入模糊控制，简写为FMCGEP[13,14]。

GEP中的基因由头部h、尾部t和DC域组成，头部包含函数符(数学函数和逻辑运算等)和终结符(求解问题的常量或者变量)，尾部则只包含终结符，DC域中基因位映射到一个与带DC域的基因对应的数组，基因尾部出现第i个“?”则对应DC域中第i个基因映射的随机常量。不同基因之间可以用函数符连接起来，头长h和尾长t的关系表达式如式(1)所示

t=h*(n-1)+1

(1)

式中：n代表操作符允许最多的参数个数。

多细胞基因表达式编程基因型网络如图1所示。

图1 MCGEP基因型网络

图1中Gen1和Gen2分别表示普通基因1和基因2，Gen1的尾部Tail中的“?”对应Gen1中DC域中的C字母，而C字母映射到常量集(Constants set)中第3个随机常量1.7601。Homeotic gene表示同源基因，同源基因尾部Tail中的1和2分别代表Gen1和Gen2。图1中MCGEP解码所得到表达式树网络如图2所示。

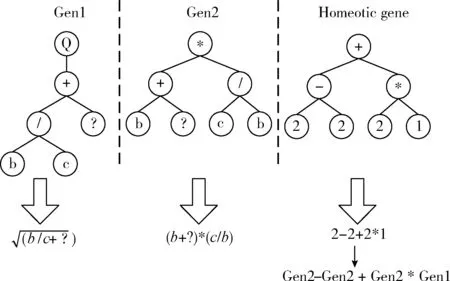
图2 MCGEP树形网络

由图2解码的表达式树最后可转换为数学表达式(2)

(2)

FMCGEP根据种群多样性来计算模糊隶属度，然后自动调节种群的交叉率、变异率和常量集变异率，增加种群多样性，使控制算法的可控性、适应性和合理性提高，从而迭代过程能够更快收敛。

1.2 CNN基本原理

卷积神经网络是受生物学上感受野机制的启发而提出，是一种具有局部连接、共享权重等特性的深层前馈神经网络[15]。卷积网络一般由卷积层、池化层和全连接层交叉堆叠组成，并通过反向传播来训练。

CNN框架中的卷积层尤为重要。图像分类任务中常用的是二维卷积，卷积网络层与层之间有若干个卷积核，上一层每个特征图与每个卷积核做卷积操作得到下一层的特征图，其卷积过程如图3所示。卷积核有长、宽、深这3个维度，长、宽需要手工设定，深度则根据输入图像维度自适应选择。CNN框架中的池化层，也称为下采样，主要用于特征降维，减小过拟合与压缩参数量，常用的池化操作有最大池化和平均池化两种，其池化核大小也需人为设定；图片经过若干个卷积和池化后，进入全连接层，全连接层多用SoftMax做分类任务。

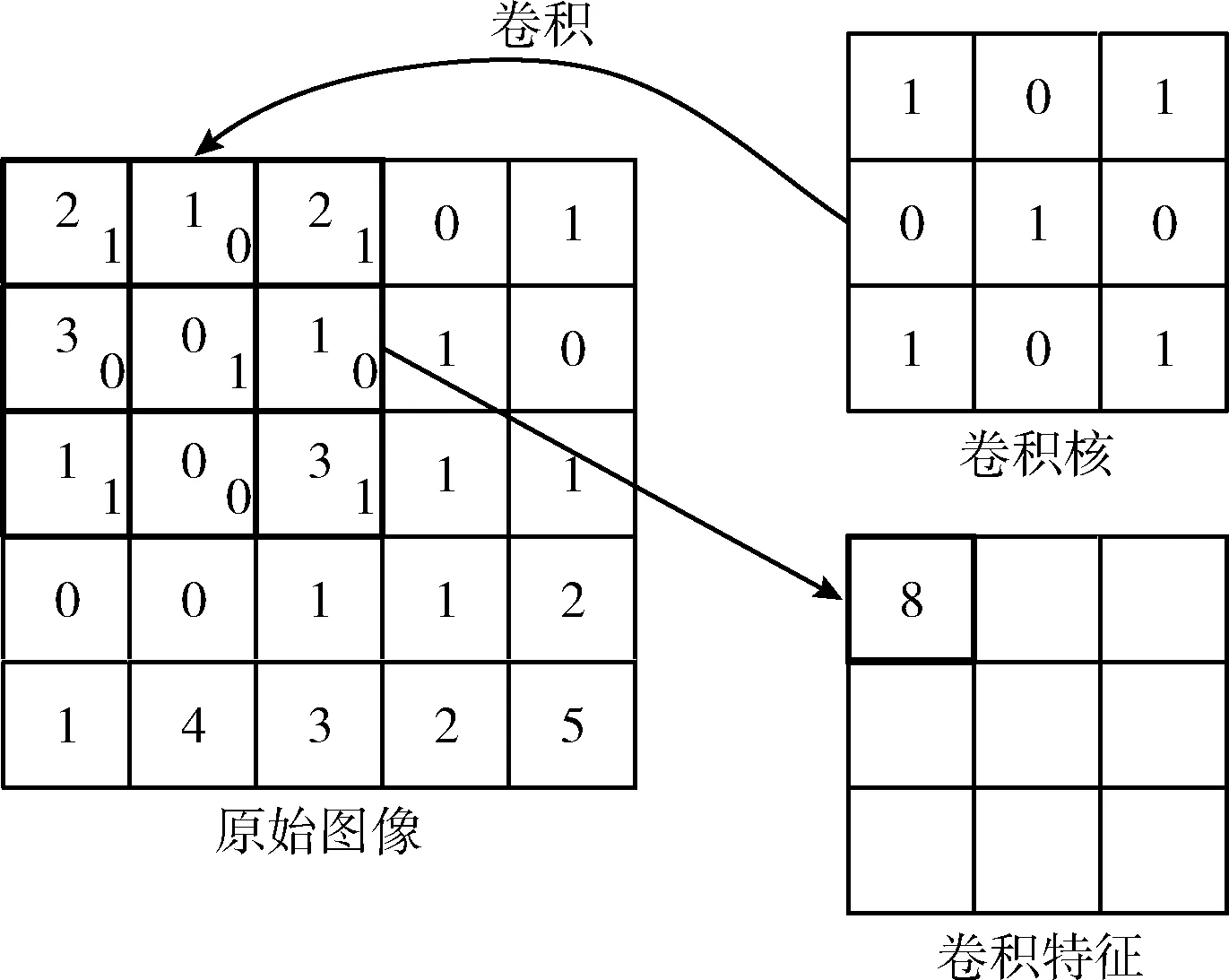
图3 卷积过程

2 基于FMCGEP构建CNN算法(FMCGEP-CNN)

本节介绍FMCGEP-CNN算法框架并对其主要组成部分进行详细讨论。

2.1 FMCGEP-CNN算法描述

算法1给出了FMCGEP-CNN的整体框架，在代码执行前先对种群进行参数设置。整个框架由5部分组成：①随机初始化种群，将CNN中待优化的设计变量编码到染色体中(见代码第(1)行)；②对染色体解码构建CNN模型，通对模型评估的值作为个体适应度值(第(2)行)；③对种群按适应度值进行排序(第(3)行)；④计算模糊隶属度值(第(4)行)；⑤通过进化得到最优的CNN神经网络(第(18)行)。在执行进化过程中第(5)-第(17)行)，先初始化一个空种群Qt来存储临时种群(第(6)行)。种群中的交叉率和变异率根据代码第(4)行计算的隶属度值判断其是否在给定的阈值范围(本文阈值范围是0.6-1)，如果不在则将初始值交叉率和变异率赋给Pc，Pm，否则执行模糊控制操作(第(10)行)。再创建临时种群q1,q2,q3,q4分别执行变异、交叉、先变异后交叉、先交叉后变异操作，最后将q1,q2,q3,q4中新产生的染色体合并到Qt中并对其排序(第(11)-第(16)行)。当种群进化迭代次数达到设定最大次数，进化终止。

算法1：FMCGEP-CNN框架

输入：种群大小N,最大迭代次数G，交叉率Pc,变异率Pm,锦标赛规模Pt。

输出：最优CNN模型。

(1)P0← Initialize a population with the size ofNby MCGEP coding strategy；

(2)Construct the CNN model, evaluate the fitness of individuals in P0;

(3)Sort P0；

(4)Calculated membership(degree);

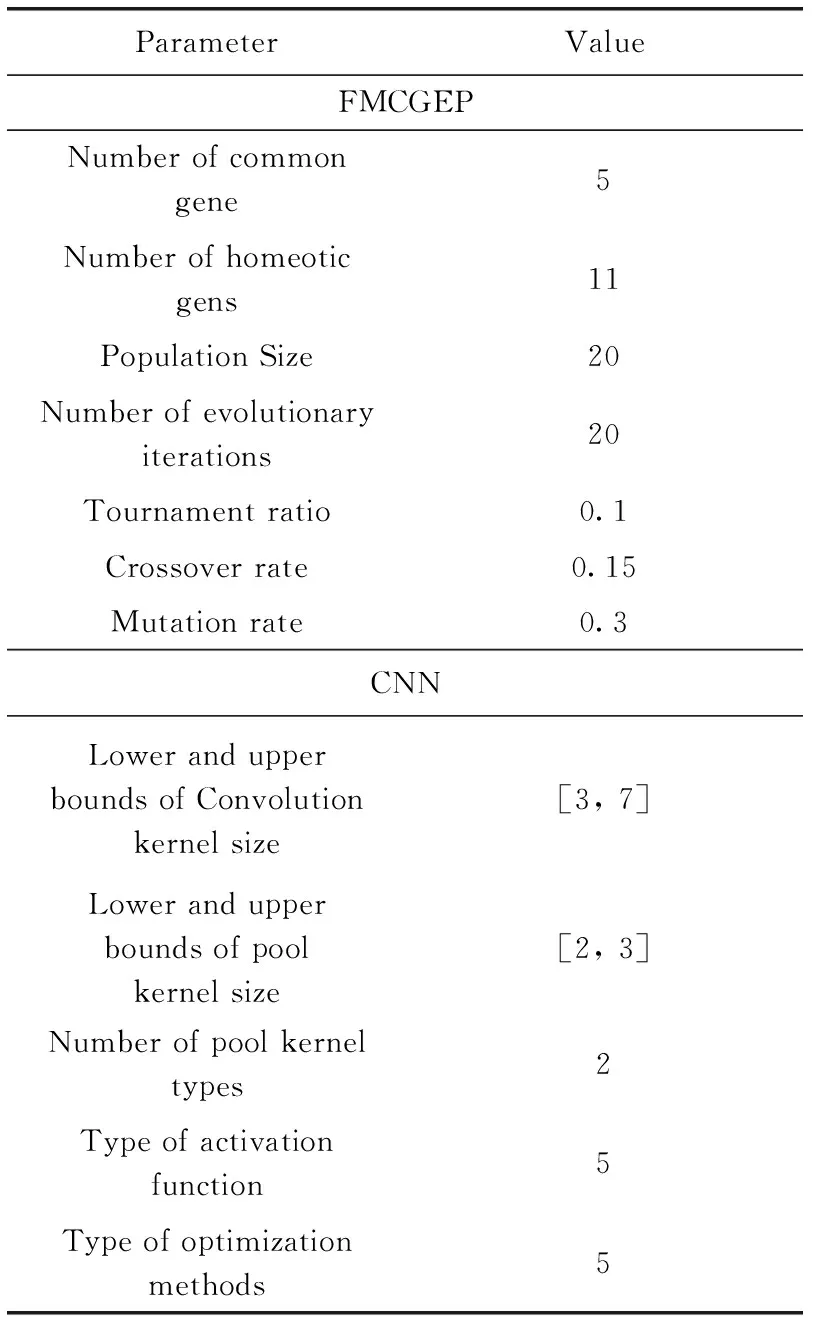
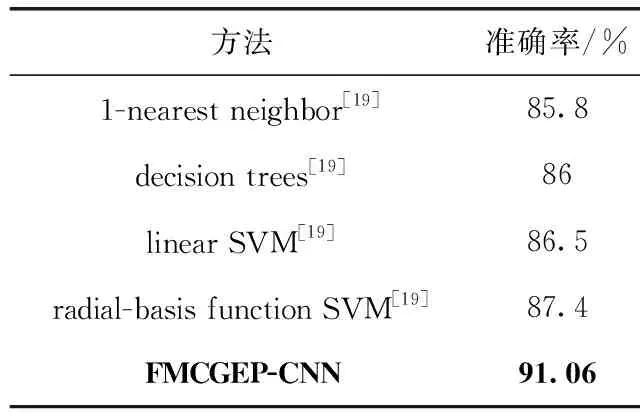
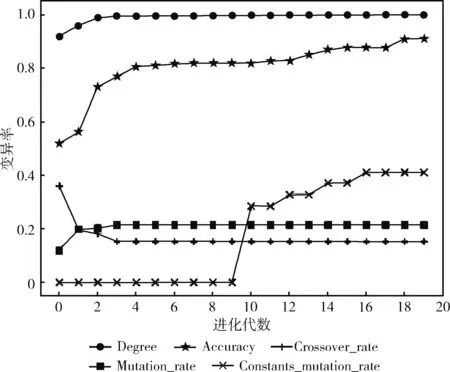
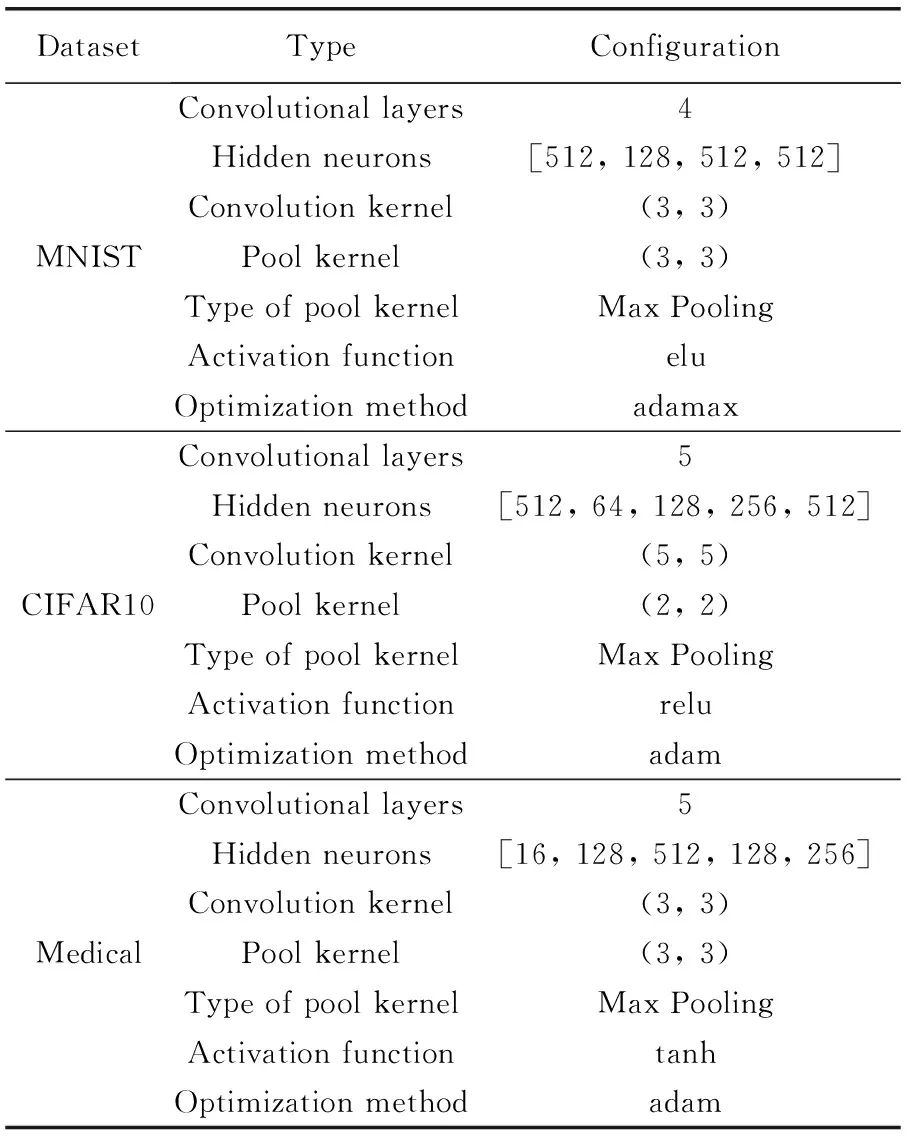
(5)While t

(6) Qt←∅

(7) While Qt

(8) if degree<0.6 or degree>1

(9)Pm=Pm,Pc=Pc; //将初始值得交叉率和变异率赋给Pm,Pc

(10) else:Pm= Mutation_fuzzy_control,Pc= Cross_fuzzy_control;

(11) q1, q2 ←do mutation operation, do crossover operation;

(12) q3 ←do the mutation first then the crossover operation;

(13) q4 ←do the crossover first then the mutation operation;

(14) Qt← q1∪q2∪q3∪q4;

(15) End

(16) Sort Qt，which population size is equal toN;

(17)End

(18)Select the best CNN from Qt.

2.2 CNN网络编码

研究表明，神经结构和全局超参数等设计变量对CNN性能影响极大。包括：激活函数、优化方法、卷积核大小、池化核大小、池化类型、隐藏神经元数量以及网络层数等[16-18]。在FMCGEP-CNN中，将待优化的设计变量编码到染色体中，假设需要优化的设计变量有M个，则用M个同源基因表示，这M个同源基因可以通过N个普通基因映射得到，N个普通基因被翻译为一个特定的实数。本文将用一个例子来详细说明编码过程，假设要优化的CNN的最大网络层数maxL等于5，可以用1个设计变量描述网络层数，用5个设计变量分别描述对应隐藏层的神经元个数。激活函数、优化方法、卷积核大小、池化核大小、池化类型各用一个设计变量描述。则以上11个设计变量可以用11个同源基因表示并编码到一条染色体中，如图4所示。该染色体由5个普通基因和11个同源基因组成。染色体中的同源基因Hgen 1至Hgen 6分别表示激活函数、优化方法、卷积核大小、池化核大小、池化类型和网络层数，第7个到(maxL+6)个同源基因分别代表第一至maxL隐藏层的神经元数。

2.3 网络模型构建

首先，FMCGEP-CNN根据相应设计变量值的假设域，随机生成如图4所示的染色体网络。然后，FMCGEP-CNN利用由染色体解码得到的设计变量构建CNN模型，其构建过程如下：

图4 MCGE染色体网络

(1)搭建卷积与池化层，使用输入数据的特征纬度、初始化卷积核、初始化激活函数以及第一层隐藏神经元个数，构建卷积网络第一层；

(2)利用初始化神经元数目和激活函数建立模型的第二至最后一层；

(3)使用Flatten函数将数据纬度拉平；

(4)在全连接最后一层设置图像分类类别以及使用SoftMax激活函数；

(5)在隐层中加入Dropout 的概率为0.2，在训练过程中随机丢弃部分模型神经元，以缓解过度拟合，提高模型泛化能力；

(6)重复(1)-(5)过程构建网络，直到网络个数等于种群数量。

2.4 网络模型训练与评估

算法2是模型训练与评估过程描述。

算法2：FMCGEP-CNN模型进化

输入：初始化种群pt，训练数据Dtrain，测试数据Dtest。

输出：最佳适应度值Fbest。

(1)For each individual in ptdo //个体训练与评估

(2) CNN←Transform the information encoded in individual to a CNN with the corresponding architecture;

(3) Train CNN model on Dtrain;

(4) Accuracy←Evaluate the classification accuracy of the trained CNN on Dtest;

(5) Assign accuracy as the fitness of individual;

(6)The best fitness value of current pt.

算法输入初始种群、训练和测试数据，输出最佳适应度值。代码第(1)行对每个个体执行进化操作；然后对个体编码的信息解码，构建CNN模型(第(2)行)；再使用训练数据训练模型，并用测试数据评估模型，评估值即为个体适应度值(第(3)-第(5)行)；得到当前种群最佳适应度值，直到进化结束(第(6)行)。

3 实验与讨论

实验的目的是验证所提出的算法对图像分类的准确率以及算法的鲁棒性。

3.1 数据集介绍

本文分别使用了MNIST数据集、CIFAR10数据集和一个医学图像数据集[19]。其中，MNIST数据集是手写数字0-9，共有60 000个训练样本和10 000个测试样本；CIFAR10数据集有50 000个训练样本和10 000个测试样本，MNIST和CIFAR10两个数据集均有10个类别；医学图像数据集来自海德堡大学病理学研究所，该数据集代表人类大肠癌组织学图像纹理的集合，包含5000个组织学图像的压缩文件夹，共8个病状类别。

3.2 FMCGEP-CNN参数设置

FMCGEP-CNN算法参数由两部分组成，一部分是FMCGEP的参数设置，如种群大小、进化代数以及锦标赛选择比例等；另一部分是卷积网络的参数设置，如卷积核上下界、网络训练次数等。FMCGEP-CNN算法参数设置见表1。

表1 FMCGEP-CNN参数设置

3.3 实验结果与分析

文中设置了3组实验，将FMCGEP-CNN算法分别与其它先进算法在MNIST数据集、CIFAR10数据集和医学数据集进行对比。本文算法与文献[20]同属进化神经网络优化算法，而该文献提出的算法(EvoCNN)在多个实验中被验证是最具竞争力的，因此在MNIST和CIFAR10数据集上将本文算法与之进行详细讨论。

3.3.1 MNIST手写数字分类实验

在MNIST数据集上，主要从分类准确率和网络迭代次数这两方面做对比分析，本文提出的算法计算网络模型迭代次数的公式为式(3)

Num=po*ge*epochs

(3)

其中，po表示种群大小，ge表示种群进化次数，epochs表示每个网络训练次数。

表2中前5个对比算法来自文献[21]。本文提出的算法FMCGEP-CNN 取得99.32%的准确率，比最差的Linear classifier算法提高了8.43%，比LeNet-5算法提高了0.12%，比大多数算法的分类准确率高。FMCGEP-CNN比迭代优化CNN[22]略低，但网络模型迭代次数降低了近5倍。由于受限于计算资源，故将FMCGEP-CNN算法和EvoCNN算法的最大网络层数均设置为5，在相同条件下将EvoCNN与FMCGEP-CNN在MNIST数据集训练、测试过程进行比较。

表2 MNIST数据集上各方法对比

从图5(a)与图5(c)中可以看出，两种算法在训练和测试准确率上大体相同，图5(b)中显示EvoCNN在训练集的损失值要小于FMCGEP-CNN损失值，但图5(d)中显示两种算法在测试集损失几乎一致，由此可知，EvoCNN存在过拟合现象。

图5 MNIST数据集实验分析

3.3.2 CIFAR10分类实验

在表3所有对比算法中，FMCGEP-CNN算法在CIFAR10数据集上表现出最好的分类效果，且迭代次数最少，相比于传统算法CIFAR10_Net来说，准确率提高了6.14%，迭代次数减少了10倍左右。残差网络是近年来较具竞争力的模型，ResNet18 网络准确率为83%，但相比本文算法略差。

表3 CIFAR10数据集上各方法对比

为了进一步验证本文算法的分类性能，将EvoCNN与FMCGEP-CNN在更大数据CIFAR10上进行论证分析。

由图6(c)中可知，FMCGEP-CNN算法在训练集上损失值较低，同时由图6(d)可知，在测试集中FMCGEP-CNN损失值低于EvoCNN，所以EvoCNN算法在CIFAR10数据集上相对于FMCGEP-CNN算法仍然存在过拟合现象。在模型训练时，两者的准确率都达到了90%，但在测试集中，本文算法略微优于EvoCNN算法，同样说明EvoCNN算法存在过拟合现象。

图6 CIFAR10数据集实验分析

图7展示了FMCGEP-CNN算法在CIFAR10数据集上进化20代过程中，分类准确率最优值与最差值的变化情况。从图中可以看出，在初始种群(即进化第0代时)，CIFAR10准确率只有67.6%，通过交叉变异等遗传操作将准确率提升至83.63%。进化过程中最差值不断提升，最优值也不断提升，最终收敛到全局最优值，找到CNN最优模型。

图7 CIFAR10数据集进化代数ACC优劣值

3.3.3 医学图像分类实验

为了验证提出算法的鲁棒性，将本文算法应用在大肠癌症数据集中，该数据集来自文献[19]，并与文献使用的算法进行对比。该文献指出，当涉及到CRC组织学图像中组织类型的分类时，所发表的文献都使用了自己的(非公开)数据集，且只考虑肿瘤和基质二分类问题，而该文献的数据可共享。

从表4可知，文献[19]中针对该数据集提出的4种机器学习分类方法分类准确率均低于90%。本文方法相对其分别提高了5.26、5.06、4.56、3.66个百分点，这说明本文方法不仅在基准数据集上实用，迁移到医学图像数据同样取得较好效果。

表4 医学数据集对比

图8是FMCGEP-CNN算法在医学图像数据集的进化代数与参数变化曲线图。图中共5条曲线按照左边第一个节点

从上往下依次表示为：Degree曲线表示的是模糊隶属度变化情况；Accuracy曲线表示分类准确率变化情况；Crossover_rate曲线表示的是交叉率变化情况；Mutation_rate曲线表示的是变异率变化情况；Constants_mutation_rate曲线表示的是常量集变化情况。由图8可知，分类准确率从第1代至第8代呈上升趋势，但从第8代至第11代，准确率变化极其缓慢，直到第12代准确率才迅速提升。准确率从第1代至第10代的变化是受种群的交叉率和变异率的影响，但是常量集变异率为0，直到第11代，常量集变化不再为0，从而增加了种群多样性，因此准确率也随之变化。该数据集的参数变化使用了模糊控制技术，动态调整交叉率、变异率、常量集变异，从而使得整个种群向最优化进化。

图8 进化代数与参数变化

3.3.4 所得的最优CNN网络

本节展示了由本文算法在MNIST、CIFAR10和医学图像数据集中分别优化得到的最好的CNN网络，见表5。训练MNIST得到的最好CNN模型有4个卷积层，用它的卷积池化核均为3*3；训练CIFAR10得到的最好CNN模型有5个卷积层，且它的卷积核为5*5，池化核为2*2；而训练医学图像数据集得到的最好CNN模型有5个卷积层，且它的卷积池化核均为3*3。3个数据所使用的激活函数和优化方法各不相同，每层隐藏神经元数也各不相同，但池化类型都选择最大池化。因此，通过进化搜索自动发现架构具有更简单的架构和更好的性能，也可能提供有用的领域专业知识，这与我们的常识形成了对比。

表5 各数据集上得到的最优CNN网络

4 结束语

本文运用模糊控制多细胞基因表达式编程算法自动优化卷积神经网络，并应用于图像分类任务。实验结果表明，本文提出的算法相对于经典算法和其它先进算法具有一定优势。本文算法网络构建过程是自动的，可以节省人力、物力和财力，该算法在图像分类建模问题中非常有效，对解决实际问题有重要意义。

尽管本文算法在自动化和分类精确度上取得了不错效果，但该算法还存在不足。首先，本算法探索的是对一般的CNN进行优化，一些特殊的网络模块如NiN、Inception等还没有被探索。

总之，本文所提出的算法为图像分类提供一种有效、可行的方法，下一步工作我们将考虑兼容更复杂神经结构块的高效优化框架及其并行化实现。