基于二维装箱问题的TTE调度表生成算法
郭袁贾
(中国航天科工集团第二研究院 七〇六所,北京 100854)
0 引 言
自时间触发以太网(time-triggered Ethernet,TTE)[1-4]概念提出以来,关于调度表生成的研究就一直在持续,调度表生成问题被认为是NP困难问题[5],目前没有算法可以求解出这个问题的精确最优解,因此大多数算法都致力于生成工程上可用的调度表。传统的调度表生成算法是例如文献[6]和文献[7]中提出的利用SMT求解器进行求解的方法。这之后出现了一些利用启发式算法对调度表进行求解的方法,例如文献[8]中使用了粒子群模拟退火算法,文献[9]中使用了模糊粒子群优化算法,文献[10]中使用了遗传算法。这些启发式算法提高了全局寻优效率,但是当通信任务较多时会导致算法运算时间快速增加,为了解决这个问题,文献[11]和文献[12]中提出了二维装箱算法和启发式算法结合的方法。混合二维装箱算法虽然降低了调度表生成的运算时间,但是仍然存在以下问题:①采用了固定的时隙来传输数据帧,虽然这样可以简化问题,但是实际工程应用中通信任务数据帧通常是不一致的;②无法满足通讯任务动态添加,调度表动态更新的需求,这导致当前的算法无法满足实际工程应用中复杂多变的实际需求。为了解决上述问题,基于二维装箱问题提出了一种调度表生成算法。
1 问题抽象建模
1.1 网络模型
本文参考了文献[5]中的模型,主要关注全双工链路下数据帧的传输,参考了文献[11]中设计的较为复杂的树形网络拓扑结构,如图1所示。图中具有18个终端节点和14个交换机节点。其中粗实线表示节点之间物理链路连接,带箭头的细实线表示一段链路上数据帧的传输方向,虚线表示一个终端节点到另外一个终端节点的通讯任务经过的链路路径。

图1 网络模型拓扑结构
对网络模型进行如下定义:
集合V(Vertex)表示网络拓扑中所有的节点,其中每个节点有一个唯一的标识i,因此网络拓扑中的节点可以表示为Vi。
集合S(Switch)表示网络拓扑中所有的交换机节点,其中每一个交换机有一个唯一的编号j,因此每个交换机可以表示为Sj,例如图中V9和S9表示同一个网络节点。
集合E(endsystem)表示网络拓扑中所有的终端节点,其中每一个终端节点都有一个唯一的编号k,因此每个终端节点可以表示为Ek,例如图中V18和E3表示同一个网络节点。
集合L(Link)表示网络拓扑中所有物理连接链路,其中节点Vi和节点Vj之间的链路可以表示为Lvivj,由于本文考虑全双工通信链路,因此Lvivj和Lvjvi认为是不同的链路。
集合VL(VirtualLink)表示网络中由一个节点链接到另外一个节点的通信链路,可以表示为VLvivj,其中VLvivj由集合L中的元素组成,同时可以表示为集合V中元素序列的形式。例如图1中由节点V18到V31的虚拟链路可以表示为VLv18v31=Lv18v8+Lv8v1+Lv1v0+Lv0v4+Lv4v11+Lv11v12+Lv12v31,同时可以表示为VLv18v31=V18V8V1V0V4V11V12V31。
集合T(Task)表示网络中所有由终端节点发送到除自身以外节点的通讯任务定义为Tvivj={id,source,desti,period,length,VLvivj},其中id表示通讯任务的标识符,scycle表示发送数据帧的节点,desti表示接收数据帧的节点,period表示通讯任务的周期,length表示任务数据帧长度,VLvivj表示通讯任务的虚拟链路路径。例如图1中由节点V31到节点V16存在一条周期为3 ms,数据帧长度为256字节的通讯任务,则可以表示为Tv31v16={1,31,16,3 ms,256 Byte,VLv31v16},其中VLv31v16=Lv31v12+Lv12v11+Lv11v4+Lv4v0+Lv0v1+Lv1v7+Lv7v6+Lv6v16。
1.2 装箱问题模型
假设从时间轴上看某一条物理链路上数据帧的传输情况,假设有两个通讯任务在物理链路上传输,一个通讯任务每次传输的数据帧很短但是周期较小,另外一个通讯任务周期长但是每次都要传输很长的数据帧。如图2(a)所示,任务1在时间轴上经常开始占用链路传输,但是每次只占用一小段时间,任务2每次发送需要占用很长时间,但是从时间轴上看,每隔很长时间才开始占用一次。
现在根据基本周期对时间轴进行折叠,如图2(b)所示,进一步把折叠的时间轴看作一个“箱子”如图2(c)所示,当链路中需要传输不同周期的通讯任务时,可以定义基本周期为所有周期的最大公约数,这样可以保证每个通讯任务在基本周期内最多传输一次,集群周期可以定义为所有周期的最小公倍数,这样可以保证每个通讯任务在集群周期中都至少传输一次并且传输次数在每个集群周期中相同。
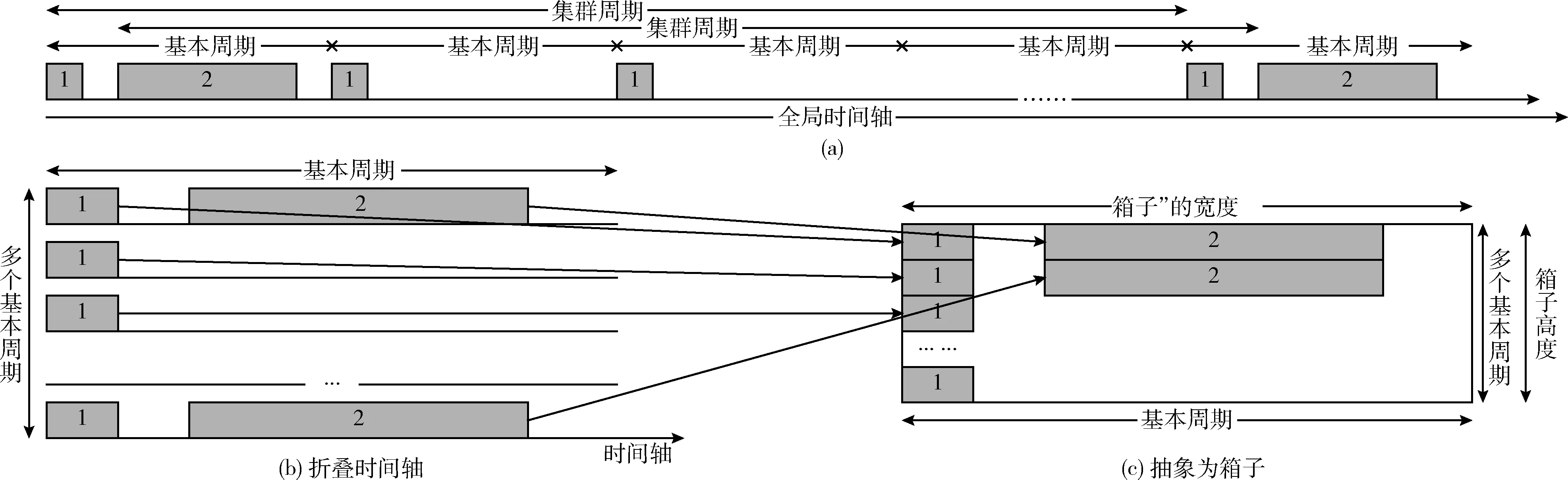
图2 装箱问题抽象过程
箱子的宽度和链路的数据传输速率有关,这里假设网络中所有的链路具有相同的数据传输速率,都为Bwidth。根据基本周期,集群周期和链路数据传输速率可以计算出“箱子”的高度和宽度如式(1)、式(2)所示,其中GCD(greatest common divisor)表示最大公约数,LCM(least common multiple)表示最小公倍数
(1)
(2)
最后,每个通讯任务可以看作一个有宽度有高度的“二维物品”,可以看出周期越小的通讯任务高度越高,而数据帧长度越长的通讯任务宽度越宽。因此把每一个通讯任务Tvivj抽象为一个“二维物品”Ovivj,将所有二维物品的集合表示为O(object)。并且可以计算每一个物品的宽度和高度,如式(3)和式(4)所示
Ovivj.width=Tvivj.length
(3)
(4)
2 二维装箱算法
2.1 通讯任务预处理阶段
改进前的算法利用交换机节点手动划分了“同步传输域”,之后定义不同“同步传输域”的通讯任务可以进行整合同时传输。这样的定义虽然可以简化问题,但是在实际网络环境中跨越多个“同步传输域”的通讯任务往往也满足同步传输的条件,因此会造成一定程度的时间资源的浪费,本文在进行装箱算法之前特别设计了预处理阶段,根据虚拟链路对通讯任务进行整合,并且只有整合后可以提高时间资源利用率的通讯任务才进行整合,这样进一步提高了时间资源利用率也避免了手动划分“同步传输域”的步骤。
以太网使用的物理链路支持全双工通信,因此接收和发送可以同时进行传输,并且虚拟链路不重合的通讯任务也可以同步传输。之前把通讯任务Tvivj抽象为Ovivj,这意味着在实际装箱的过程中,有的物品可以和其它的物品重叠,如图3(a)所示。
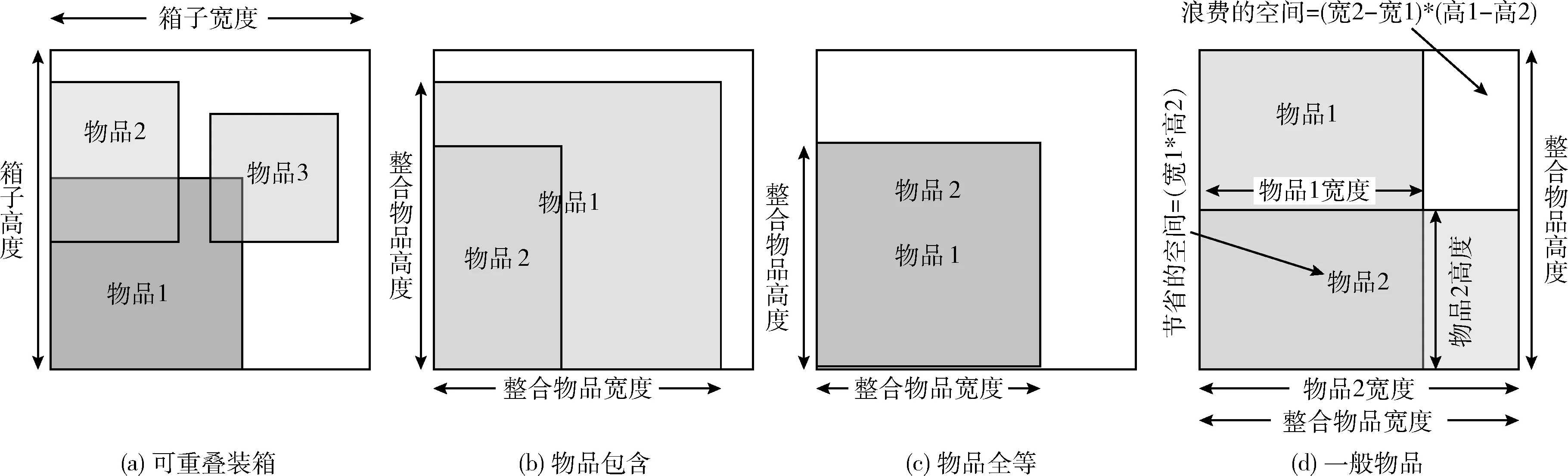
图3 通讯任务预处理
假设现有两个通讯任务Tvivj和Tvmvn,它们的虚拟链路路径可以表示为VLvivj=Lvivk+…+Lvpvj,VLvmvn=Lvmvx+…+Lvyvn。当对于Tvivj中所有L都不等于Tvmvn中的L,则认为Tvivj和Tvmvn可以同步传输,这也表示Ovivj和Ovmvn可以重叠。
当Ovivj和Ovmvn可以重叠时,可以把Ovivn和Ovmvn合并为一个物品。此时存在3种情况如图3(b)、图3(c)、图3(d)所示。当一个物品可以被另外一个物品包含时如图3(b)所示,可以认为大物品的宽度和高度就是新整合物品的宽度和高度。当两个物品完全重合时如图3(c)所示,可以把两个物品认为是一个物品。图3(d)是最常见的情况,当两个物品只能部分重叠时,这时需要对节省的空间和浪费的空间进行计算,当节省空间大于浪费空间时可以进行物品整合,否则不对物品进行整合。整合后的物品依然可以和其它物品继续整合,不过此时要求整合物品中的原始物品通讯链路两两不重合。
2.2 装箱算法阶段
经过通讯任务预处理阶段,所有物品认为只能互相不重叠地进行装箱。
为了规范装箱的过程并且简化装箱算法的实现,本文定义了集合P表示目前箱子中的“可用装箱点”,如图4(a)所示,当箱子为空时,只存在一个装箱点P0(0,0),当装入一个物品时只能选择现有的装箱点进行放置,因此放入第一个物品会消耗“可用装箱点”P0(0,0),同时会产生两个新的装箱点如图4(b)所示P1(Ovivj.width,0)和P2(0,Ovivj.height)。同理可知,当放入第2个物品时只能选择现有的装箱点P1或者P2,如图4(c)和图4(d)所示,此时会消耗一个“可用装箱点”,同时根据放入物品的宽度和高度可以计算出新增加的“可用装箱点”。
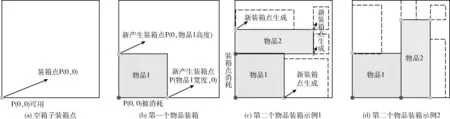
图4 装箱点
为了简化“可用装箱点”的生成位置,可以把物品按照高度和宽度进行排序,此时后放入的物品高度和宽度必然小于等于之前放入的物品。如图5(a)和图5(b)所示,此时就自然避免了图4(c)和图4(d)中出现的情况,这样可以保证每放入一个物品都只会消耗一个“可用装箱点”同时会产生至多两个新的“可用装箱点”,当后放入的物品宽度或者高度与前一个物品相同时只会消耗一个“可用装箱点”同时产生一个新“可用装箱点”,如图5(c)和图5(d)所示。

图5 排序后物品装箱
在算法的实现过程中,使用一个数组型数据结构就可以方便的存储“可用装箱点”信息,只需要改变数组中“可用装箱点”的选取策略就可以改变装箱算法的装箱策略。此外,保存运行装箱算法过程中产生的“可用装箱点”有利于新通讯任务的动态添加,如果在之前的“可用装箱点”记录中可以找到合适的装箱位置,则新通讯任务的添加不需要重新运行装箱算法也不需要修改已有的调度表,只需要对新通讯任务对应的调度表表项进行添加即可。同时也可以简化调度表分发的过程,此时由于其它调度表项都不变,因此可以只发送新通讯任务的调度表表项到对应的交换机节点即可。
综上所述,装箱算法流程如图6所示。

图6 装箱算法阶段流程
2.3 调度表表项计算阶段
改进前的算法没有对最后如何生成实际可用的调度表进行详细论述,装箱算法对链路的时间资源进行了抽象和分配,可以保证数据帧没有冲突的传输,但是在实际网络环境中,链路存在传输时延和传播时延,交换机存在转发时延,这些因素在实际使用中必须要考虑进去,并经过计算才可以得到实际的数据帧发送时间点和接收时间点。
图7(a)是整合后的物品的装箱结果示意图,整合后的物品只能不重叠地进行装箱。在通讯任务预处理阶段将可以同步传输的任务整合为一个物品,整合的物品在计算调度表时需要恢复成原始物品,图7(b)是整合物品恢复成原始物品后的装箱结果示意图,例如图7(a)中的整合物品C在图7(b)中被还原为原始物品③和⑦。图7(c)是物品还原到每个基本周期传输的示意图,这个过程与时间轴折叠抽象为箱子的过程正好相反,“箱子”是由多个基本周期组合而成的,此时需要将通讯任务根据装箱结果分散到基本周期中。图7(d)是数据帧在链路上传输,这里是忽略了传输时延和转发实验的传输,当考虑时延影响时,数据帧在链路上的传输如图7(e)所示,例如数据帧从链路1传输到链路2有时延并且采用存储转发策略,因此链路2开始发送数据帧的时间会比链路1延后,之后通过的链路同理。

图7 调度表表项计算阶段
综上所述可以对装箱算法的结果进行解析和计算然后得到数据帧在每条链路上的发送时间点和接收时间点,之后根据全局时钟精度加上发送窗口和接收窗口就可以得到实际应用中可用的时间调度表表项。
2.4 动态添加通讯任务
当需要在已经计算好的时间调度表中加入新的通讯任务时,如果之前使用的是例如文献[8]或者文献[9]中的启发式算法,这时就需要把新的通讯任务加入通讯约束之后重新运行算法才可以得到新的调度表,这样无法满足实际应用中复杂多变的实际需求。本文设计的三阶段装箱算法可以在一定程度上满足动态添加通讯任务然后生成对应的调度表项。
在第二阶段装箱算法中保存了整合后的物品信息以及当前的“可用装箱点”信息,因此当有新的通讯任务请求计算调度表时,可以直接与当前整合后的物品进行整合性判断,如果可以与当前的某个物品整合,那么直接根据当前整合物品的装箱结果就可以计算得到该通讯任务对应的调度表。如果该任务与当前所有物品都无法进行整合就读取“可用装箱点”信息,如果有可以容纳该通讯任务的装箱点,那么根据装箱结果也可以计算得到该通讯任务的调度表信息。最后如果当前添加的通讯任务既无法与当前物品整合也无法找到“可用装箱点”,此时才把该通讯任务加入通讯任务约束并重新运行装箱算法,得到所有物品新的装箱结果并重新计算所有物品的调度表。
3 仿真实验及讨论
3.1 仿真实验网络设置
本文进行实验时选用了文献[11]中设计的较为复杂的网络拓扑结构,如图1所示。本文在装有Matlab2016的Windows10上进行仿真实验,处理器为Intel(R)Core(TM)i5-4210U CPU@ 1.70 GHz 2.40 GHz。
本文关注支持全双工通信的以太网链路,但是现有的装箱算法关注于单工模式传输。为了与之前研究保持实验条件一致,本实验中也假设网络中所有链路处于单工模式,即在物品整合过程中认为链路Lvivj和Lvjvi是同一条链路不能同步传输。
为了简化仿真实验,本文假设网络拓扑中所有链路的传输速率都为100 Mbit/s,由于本次实验关注于时间资源的占用情况,因此忽略网络链路中的传输时延、传输时延、交换机中的转发时延,这些时延只会影响调度表的发送时间点和接收时间点而不会影响链路的时间资源占用情况。
3.2 随机通讯任务设置
本文设计的算法支持每个通讯任务具有不同的数据帧长度,但是之前的装箱算法为了简化模型认为每个通讯任务都在固定的时间间隙传输,因此本文实验中也保持每个数据帧的长度相同,这里假设每个数据帧长度为64个字节。
本文设计了随机通讯任务来检验算法的时间资源占用情况。这里只考虑终端节点之间的通讯,不考虑交换机节点主动向终端节点发送数据,也不考虑交换机之间的通讯。随机选取集合E中的一个节点Ei,再随机选取一个不同的节点Ej,因此Ei到Ej通讯任务可以定义为Tvivj={id,source,desti,period,length,VLvivj}。其中id为生成随机任务时初始化的标识,一般从0开始递增,source为集合E中随机选取的一个节点,desti为集合E中与source不同的节点。period为{N1*1 ms,N2*2 ms,N3*3 ms,N4*5 ms,N5*7 ms,N6*9 ms,N7*10 ms}中随机选取一个值,其中N1到N7为大于等于1小于等于10的整数。Length固定为64字节。VLvivj为根据图1所示拓扑计算得到的虚拟链路路径。
重复从集合E中选取两个不同节点并计算虚拟链路的步骤,这样可以得到多个网络中的随机通讯任务。
3.3 实验结果及讨论
仿真实验使用的指标是文献[9]中定义的时间资源占用率,由于通讯任务已经抽象为了“二维物品”所以这里使用“箱子”的空间占用率代表时间资源占用率(Occupancy),占用率计算公式如下
本仿真实验利用3.2中介绍的随机通讯任务生成方法分别对网络中同时存在50个通讯任务、100个通讯任务等情况进行了仿真实验。其中每种情况重复了10次随机实验以消除随机误差。实验结果见表1。

表1 链路时间资源占用率/%
将随机实验的平均值绘制为折线如图8所示。
由折线图可知当网络中同时传输的通讯任务数量增加时,网络的时间资源占用率也在增加,这和实际网络中数据帧的传输现象相符的。由于实验中通讯任务的周期是随机数,数据帧的发送节点和接收节点都是随机选取的,因此网络中虽然同时存在的通讯任务数量相同但是时间资源占用率却不同,例如网络中只存在10个通讯任务时,第2次实验和第8次实验时间资源占用率差别较大,这是因为第8次通讯任务随机生成的周期都较小,并且为了和改进前算法的实验条件保持一致,本实验中固定所有通讯任务数据帧长都为64字节,这意味着小周期任务占用时间资源多,因此导致总时间资源占用率变大。
从图8可以看出,当网络中通讯任务数量较少时,改进前后的算法占用率基本相同没有占用过多的时间资源。当网络中同时传输的任务越多时,改进后的算法对时间资源占用率相比改进前的算法越低。当网络中同时存在550个通讯任务时,改进后的算法比改进前降低了占用率27.2%,当然,在实际的工程应用中一般不会给时间触发数据预分配这么多的链路资源,因此实际使用中也可能不能降低那么多。根据随机实验可知,当给时间触发数据分配30%链路资源时,改进后的算法能够降低时间资源占用率11%左右,体现了改进算法的在降低时间资源占用率方面优于之前的算法。

图8 不同任务数量下链路资源占用率
4 结束语
本文基于二维装箱问题对时间触发以太网调度表生成问题进行了抽象,把网络中需要分配时间资源的通讯任务抽象为具有高度和宽度的“二维物品”,并根据网络传输的特性对“二维物品”进行了预处理,之后提出了便于快速实现的装箱规则,最后根据网络中的时延计算得到实际的调度表发送时间点和接收时间点。本文设计的算法对通讯任务重新进行了抽象定义,使得通讯任务可以使用不同的数据帧长度,弥补了之前算法使用固定时隙传输的缺点。此外本文设计的三阶段装箱算法可以支持在已经生成的调度表中动态添加通讯任务,弥补了之前静态调度表生成算法的不足,提高了时间触发以太网在实际应用中的灵活性。
仿真实验结果表明,本文提出的算法在网络中同时存在较多通讯任务时可以有效降低链路的时间资源占用率。

