考虑异常因素的机械加工生产智能排程方法研究*
袁梦阳,杨晓英,张 琪,肖博文
(河南科技大学 机电工程学院,河南 洛阳 471003)
0 引 言
作为传统制造业的重要组成部分,机械加工生产企业为了应对客户个性化需求,目前已初步形成了产品按客户需求进行设计,按订单进行生产的模式,具有产品类型多、结构复杂、制造周期长、生产使用的设备以通用型为主等特征。然而,现行的生产作业排程优化模型与规则结合不紧密、算法智能化程度低,导致面对异常情况响应速度慢、生产不精益。为此,研究能够快速响应需求,且具有智能决策功能的机械加工生产作业排程,实时、动态、智能地完成生产作业计划的制订,对促进企业转型升级具有重要的理论意义和应用价值。
机械加工生产作业排程属NP-hard问题,目前具有代表性的成果有:
(1)模型方面:孙华岳、杨晓英等人[1,2]以某重机企业为研究对象,在改进田口质量损失函数的基础上,建立了质量、工期与成本之间的非线性关系;吴子轩、李铁克等人[3,4]将工艺路线这一因素引入热轧钢管订单的生产中,建立了以最佳工艺路线切换、准时化制造和最小化机器设备调整为优化目标的排程模型;CARLIE J等人[5]研究了机器无空闲约束的最小化大完工时间问题,证明了这类模型是集中于任务完成时间分段线性递减和非线性的单机排程问题;
(2)算法方面:吴永明等[6]设计了一种求解排程模型的GA-IPSO算法;GONG X等[7]设计了一种模因算法用于解决具有工人柔性的多目标柔性车间调度;ZHENG X等[8]提出了一种基于知识导向的果蝇优化算法求解具有双资源约束的柔性作业车间调度问题等。
综合国内外研究现状[9-12]:对机械加工生产排程方法的研究日趋成熟,但主要针对模型与算法方面进行相关改进,尚未将规则、模型、算法三者相互结合。在实际生产过程中会发生各种异常情况,现行的排程模型和算法面对异常情况响应速度慢,难以实现智能化排程的目标[13-15]。
本文以某重型机械产品为研究对象,考虑生产过程中的实际情况,提出基于异常因素的动态排程规则和优化模型;综合考虑工艺、生产、设备等约束,运用运筹学方法,建立以最小完工时间和最低能耗为目标的生产排程模型;采用非支配排序遗传算法求解多目标优化模型,研究该方法对车间生产过程中发生的异常情况时的响应能力。
1 考虑异常因素的动态排程规则
1.1 异常因素
由于机械加工属于订制化生产模式,生产周期长,加工过程错综复杂,插单、撤单及故障等异常现象时有发生。常见的异常因素主要包括以下几个方面:
(1)订单异常:包括急件订单插单、订单交货期临时发生改变以及订单撤单等需求变化情况;
(2)机床异常:包括机床出现故障和正在被修复等情况;
(3)质量异常:包括加工过程出现加工质量和毛坯质量等情况;
(4)物料异常:包括物料缺失、物料供给不及时以及物料质量问题等情况。
1.2 基于异常因素的动态排程规则
生产过程中发生异常情况需进行智能响应,在此基础上提出基于异常因素的动态排程规则,能够实时应对生产过程中的环境变化,能够快速有效地处理生产过程中发生的异常。
为了解决机械加工生产智能排程这一问题,本文采用滚动窗口技术来实现动态排程。将订单的各道工序分为紧急工序集、窗口工序集和已完成工序集3个集合:
(1)紧急工序集就是两次动态排程之间出现的新任务工序;
(2)窗口工序集就是当前排程优化区间中正在进行任务的工序集合;
(3)已完成工序集是已经加工完成任务的工序集合。
如果一道工序任务在新一轮动态排程开始之后到达,则该工序加入紧急工序集,并等待进入窗口工序集。当某一工序任务加工完毕,该工序从窗口工序集进人已完成任务工序集。
规则1:订单异常排程规则。当插单现象发生时,将该订单上工件所涉及的工序和其余工件未完成工序放入紧急工序集中,形成新的滚动窗口,进行新一轮的动态排程。当撤单现象发生时,将该订单上工件所涉及的工序从窗口工序集和紧急工序集中删除,其余工件未完成工序放入紧急工序集中,形成新的滚动窗口,进行新一轮的动态排程;
规则2:机床异常排程规则。机床发生故障时,机床无法正常使用,需要在上面进行的工序和其余工件未完成工序放入紧急工序集中,形成新的滚动窗口,进行新一轮的动态排程。异常的机床被修复后,机床可以正常安排工序,形成新的滚动窗口,进行新一轮的动态排程;
规则3:质量异常排程规则。工序返工发生时,返工工序和其余工件未完成的工序加入紧急工序集中,形成新的滚动窗口,进行新一轮的动态排程。工件报废发生时,将该工件所涉及的工序从紧急工序集中删除,将该工件所有的工序和其余工件未完成工序放入紧急工序集中,形成新的滚动窗口,进行新一轮的动态排程。
规则4:物料异常排程规则。当物料发生异常时,将未完成的工序加入紧急工序集中,形成新的滚动窗口,等待物料到来,进行新一轮的动态排程。
当异常情况发生时,对新的滚动窗口中的紧急工序集和窗口工序集中的工序进行动态排程。考虑转运物流浪费,未涉及故障的机床继续对原工件进行加工,发生故障机床上的工件选择其他合适且空闲的机床进行加工。
2 精益化的排程优化建模
2.1 问题描述
机械加工订制化的生产模式是为了满足客户个性化需求,其生产周期长,生产过程中会发生插单、撤单、机床故障等异常情况。要求制订生产计划时,在满足正常生产前提下,实现高质量、高效率、低成本地完成生产任务的目标。因此,优化模型既要保证产品质量,又要保证生产进度,同时要兼顾成本费用。车间的作业排程如何智能响应订单需求与生产异常,如何实时动态应对车间现场环境复杂多变,如何实现精益化与智能化排程,成为当前急需解决的关键问题。
已知条件:(1)产品零件需求类型、数量、交货期;(2)机床的类型及数量;(3)产品零件加工各道工序对应的机床集合,在各机床上的加工时间和能耗。
假设条件:(1)车间内各台机器相互独立,不同零部件的加工顺序不存在先后关系;(2)每个工件只有完成上一道工序后,才能加工下一道工序;(3)每台机床上完成现有的加工任务后,才能进行下一个加工任务;(4)每个工件的加工过程是连续进行的;(5)工件各道工序的工时定额是确定的,且在加工过程中不会发生改变。
基于以上条件,需要解决的关键问题是:建立机械加工生产作业排程优化数学模型,以最小完工时间和最低能耗量为优化目标,把每个工件的每道工序安排在最合适的机床上,并通过智能算法和异常驱动规则,自动给出每台机床上每道工序的最佳顺序和开始加工时间,使其能够快速响应异常情况的发生。
2.2 优化模型
产品零件生产过程主要涉及毛坯的加工、半成品的转运及成品质量检验等过程。对于机加过程,零件的加工时间和车间能耗量是重要考量标准。因此,本文以零件最小完工时间和最低能耗量为目标,进行优化建模。
(1)最小完工时间为各工件各道工序的完成时间减开始时间后与宽放时间之和的最大值的最小值,表示如下:
(1)
式中:ski—工序Oki的开始时间;cki—工序Oki的完成时间;ε—系统层允许的宽放值;J—工件集,J={1,2,…,k,…,n};Ik—工件k包含的总工序数。
(2)车间的最低能耗量由车间固有能耗E1、空转能耗E2和加工能耗E3组成,表示如下:
FE=Min(E1+E2+E3)
(2)
其中,车间固有能耗E1为车间固定功率与工件完工时间的乘积,表示如下:
(3)
式中:α—车间固定功率。
空转能耗E2为机床m的开机空闲时间与其固有功率的乘积,表示如下:
(4)
式中:xkim—如果Oki可以在机床m上加工,则xkim=1,否则xkim=0;EPm—机床m的固有功率;M—机床集合,M={1,2,…,m,…,o}。
加工能耗E3为各工序在机床m上的加工时间与其加工功率的乘积,表示如下:
(5)
式中:Pm—机床m的加工功率。
综合以上分析,本文对完工时间、能耗同时取最小值,建立多目标优化模型如下:
F=(MinFT,MinFE)
(6)
同时满足以下公式:
ski+xkim×tkim≤cki,k∈J,i∈P,m∈M
(7)
cki≤sk(i+1),k∈J,i∈P
(8)
ski+tkim≤shl+L(1-ykihlm),k∈J,h∈J,i∈P,
l∈P,m∈M
(9)
cki≤sk(i+1)+L(1-ykih(l+1)m),k∈J,
h∈J,i∈P,l∈P,m∈M
(10)
(11)
ski≥0,cki≥0
(12)
式中:L—一个足够大的数;P—所有工件的工序集,P={pki,k=1,2,…,n;i=1,2,…,Ik};ykihlm—如果Oki先于Ohl在机床上加工,则ykihlm=1,否则ykihlm=0。
式(7,8)表示工序的顺序约束,式(9,10)表示同一时刻同一台可用机床只能加工一道工序,式(11)表示同一时刻一道工序只能选择一台机床进行加工,式(12)表示各参数变量均为正数。
3 算法设计
3.1 NSGA-Ⅱ算法
针对机械加工生产排程模型具有多目标、多约束、非线性等特点,普通的算法难以取得较好的求解效果,本文采用带精英策略的非支配排序遗传算法,结合考虑异常因素的动态排程规则,对模型进行求解。
笔者考虑异常因素的动态排程规则进行优化求解,首先确定滚动窗口中紧急工序集中的各道工序,将各道工序往合适的机床上进行排程。
NSGA-Ⅱ算法流程图如图1所示:
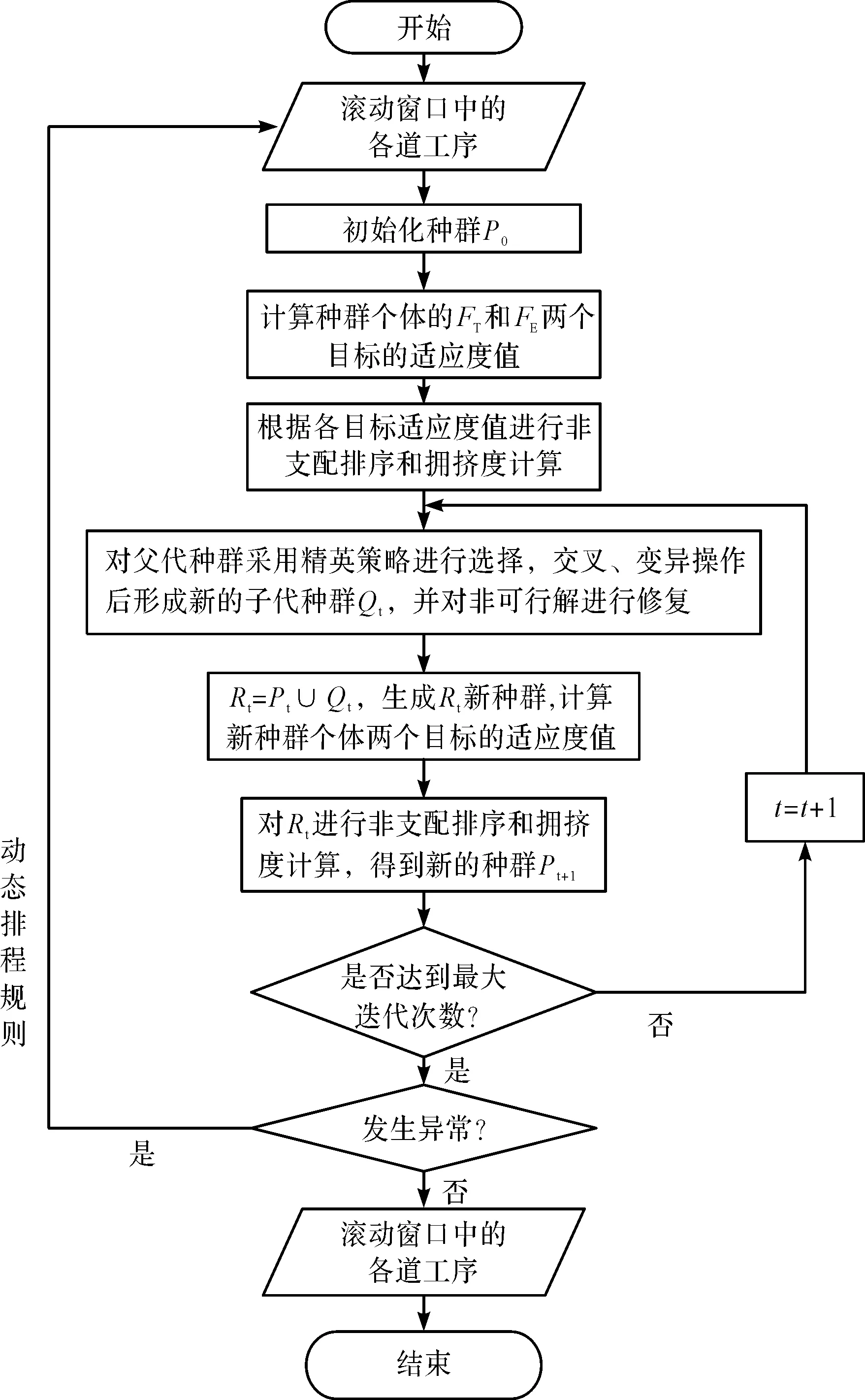
图1 NSGA-Ⅱ算法流程图
3.2 算法具体设计
3.2.1 编码和解码设计
本文采用分段编码法对染色体进行编码,染色体由机床选择和工序选择两个部分组成,长度为2a,2a表示所有工件涉及工序的总和,机床选择和工序选择均采用间接编码的方式得以实现。用k表示某个工件的序号,则k在工序选择中第几次出现就是该工件的第几道工序。在机床选择当中,每道工序可对应一台或几台相应的机床进行加工。机床选择的数值表示为第一个工件的第一道工序到最后一个工件的最后一道工序,各工序所选择的机床号。这样,机床选择和工序选择就能够相对应起来,这样能大幅度缩减查找时间,对查找最优解的效率是很有提高的。
解码过程通过从左到右遍历工序选择部分的染色体,确定工件号和工序号;然后根据所确定的工件号和工序号,对应可得到其加工机床和加工时间。
3.2.2 初始化种群和适应度计算
随机产生一个样本容量为N的种群,其中每个个体均用一条染色体表示。对于每一条染色体,在保证所有工件的所有工序数量均满足条件的情况下随机产生一个工序选择序列,在保证该工件工序所对应机床能够使用的情况下随机产生一个机床选择序列。本文通过局部搜索、全局搜索和随机搜索等相结合的方式产生初始种群,能够保证种群的基因的多样性和初始解的质量,以此大幅减少查找可行解需要的时间。
由于目标函数都是求最小值的函数,本文直接将目标函数作为适应度函数。基于染色体所代表的方案,计算种群中每个个体的目标函数值FT和FE。
3.2.3 快速非支配排序算子设计
把Pareto域最优解作为最优目标,需进行非支配排序和拥挤距离计算。在此之前,需要考虑:每道工序可以选择在不同的机床上进行加工、每台机床在同一时刻只能加工一道工序、同一工件只有完成前一道工序才能进行下一道工序等约束。首先找出群体中的非支配解集,记为第一非支配层G1,其中的个体被赋予非支配序irank=1,并从整个群体中删除;然后继续找出剩余群体中非支配解集,记为第二非支配层G2,其中的个体被赋予非支配序irank=2;照此进行下去,直到整个种群分层完成,相同非支配层中所有个体均具有相同的非支配序irank。
3.2.4 拥挤距离算子设计
个体拥挤距离是为了能够在具有相同的irank个体内进行选择性排序。个体i的拥挤距离指目标空间中与i相邻的两个体i+1和i-1之间的距离,其计算步骤为:
(1)同层的个体初始化距离。令L[i]d=0(其中L[i]d—任意个体i的拥挤距离);
(2)同层的个体按FT、FE中一个函数值升序排列;
(3)排序边缘上的个体具有选择优势,给定一个大数Z,令L[i]d=L[0]d=0;
(4)排序中间的个体,求拥挤距离:
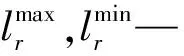
(5)分别对目标函数FT和FE重复步骤(2)~(4),使得出的结果能够在目标空间较均匀地分布,以此维持种群的多样性。
3.2.5 选择
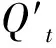
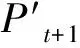
3.2.6 交叉和变异
由于机械加工生产各道工序涉及一台或多台机床,各工件涉及的工序也有先后约束。本文采用洗牌交叉方式随机选择交叉个体,将一个父基因取一半,再加上来自另一个父基因的一半,构成一个新基因。这样能够扩大遗传算法可行解中的搜索范围,提高了算法的搜索能力,对获得最优解提供有力的保证。
基于工序的染色体交叉操作是将原染色体固定不变,两父代个体的其他工序依次进行交换,该操作仅仅改变了工序顺序,机床信息和其他加工信息并没有发生改变。基于机床的染色体交叉操作是将原染色体的各道工序进行交换,工序顺序没有发生改变,改变的只是原染色体各道工序所对应的机床。加工信息是与工序和机床相互对应的,因此加工信息也随之发生改变。
变异采用基于工序的变异和基于机床的变异两种方式,其变异过程是独立进行的。假设工序总数为I,则基于工序的变异过程为随机产生1-I的两个自然数n1和n2,且n1≠n2,将n1和n2对应的工序互换。由于互换操作可能会使同一工件前后两道工序的加工顺序颠倒。
基于工序的流程修复图如图2所示。
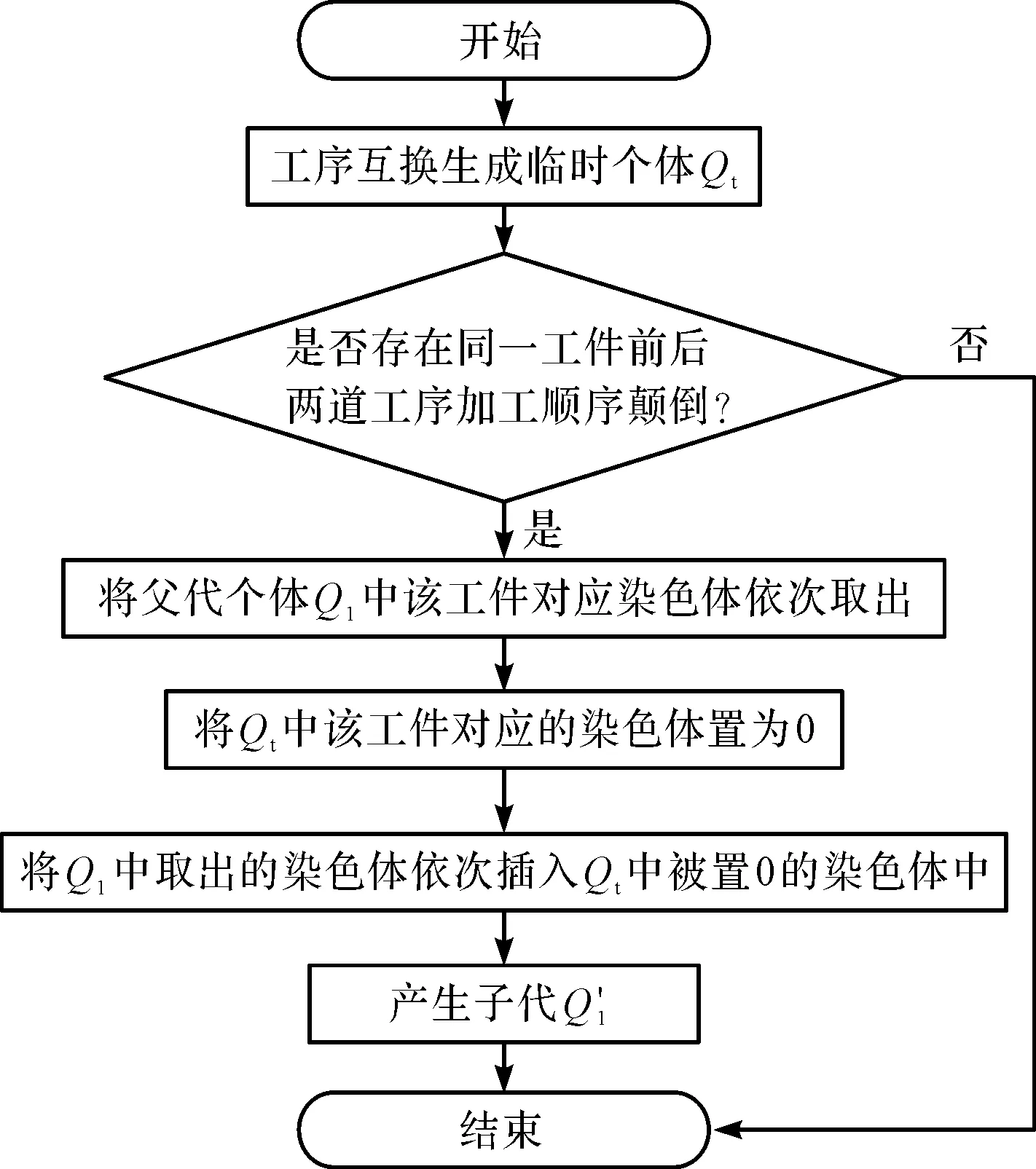
图2 基于工序的流程修复图
4 实例验证
本文排程研究对象以某重型机械产品为例。该重型机械产品主要由筒体、传动装置、窑衬、窑尾密封、燃料装置等部分组成。
该重型机械产品关键零部件信息表如表1所示。
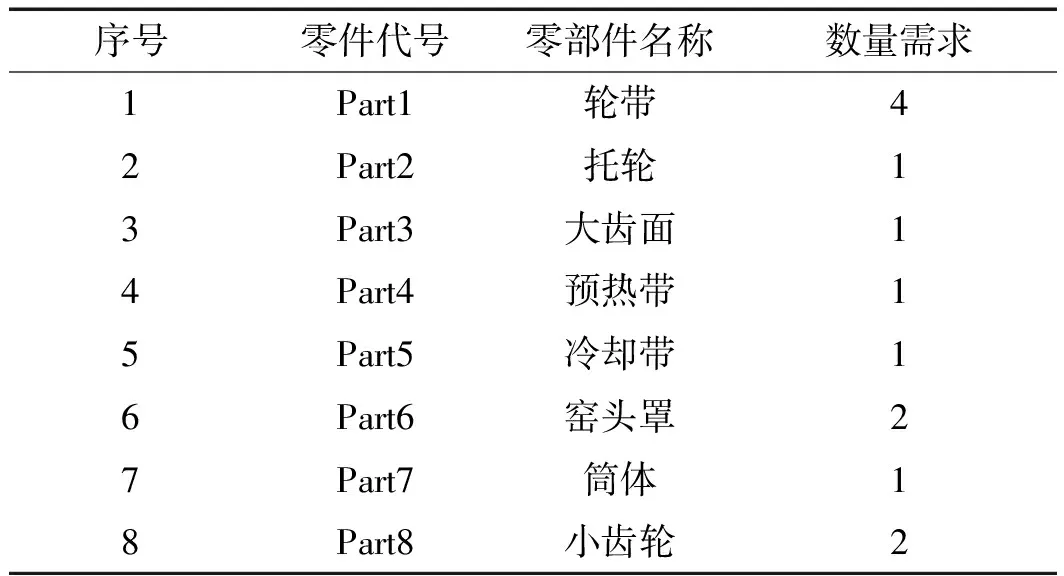
表1 该重型机械产品关键零部件信息表
以该车间车床、铣床、钻床等8台机床作为实际生产中所使用的机床,进行生产计划的安排,设备代码、设备名称、加工功率表如表2所示。
轮带、拖轮、筒体、大齿面等零部件可在一个机床或多个机床上进行加工,零件加工机床及工时定额表如表3所示。
基于以上数据分别对生产开始前发生异常和生产过程中发生异常进行实例验证。正常排程所得的甘特图如图3所示。

表2 设备代码、设备名称、加工功率表
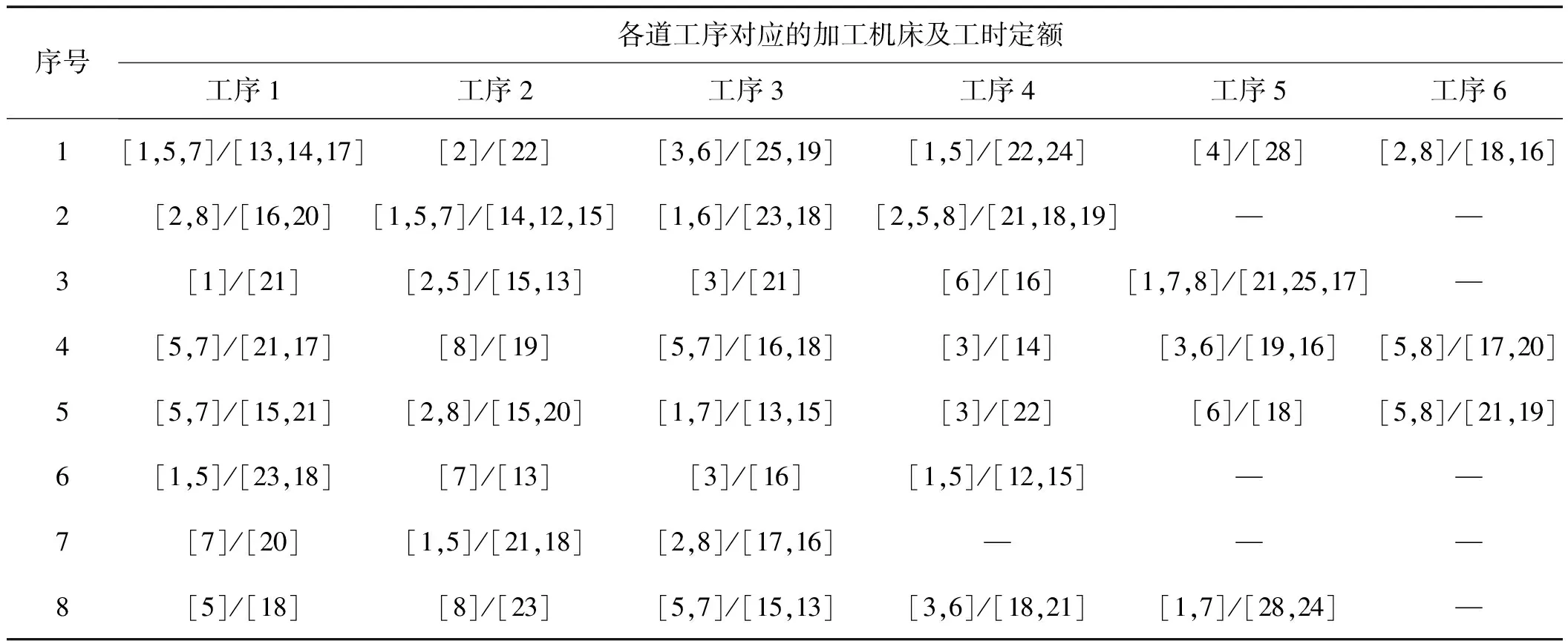
表3 零件加工机床及工时定额表
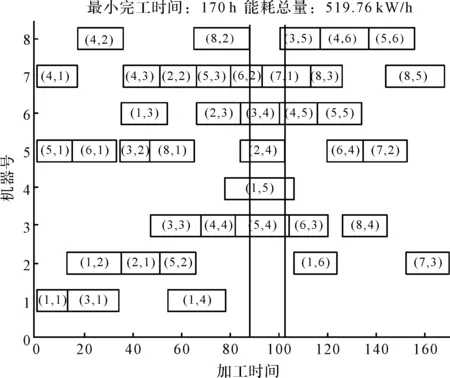
图3 正常排程得到的甘特图
各道工序均得到最好的安排,此时,最小完工时间为170 h,能耗总量为519.76 kW/h。
(1)生产开始前机床发生异常
在84 h,发现M5数控卧车出现故障,此时该设备上按照正常生产计划进行排的第2个工件的第4道工序、第4个工件的第6道工序、第7个工件的第2道工序需在该设备上进行加工。
发生设备故障,紧急订单窗口进行动态响应,第2个工件的第4道工序被转移到M2北京龙门铣床上进行加工;第4个工件的第6道工序被转移到M8科堡龙门铣床上进行加工;第7个工件的第2道工序被转移到16 M立车床上进行加工。
生产前发生异常进行动态排程的甘特图如图4所示。

图4 生产前发生异常进行动态排程的甘特图
生产开始前发生异常的集合如表4所示。

表4 生产开始前发生异常的集合
(2)生产过程中机床发生异常
在102 h,发现M8科堡龙门铣床出现故障,此时该设备上按照正常生产计划进行排的第3个工件的第5道工序、第5个工件的第6道工序、第7个工件的第3道工序需在该设备上进行加工。
发生设备故障,紧急订单窗口进行动态响应,第3个工件的第5道工序被转移到16 M立车床上进行加工;第4个工件的第6道工序和第5个工件的第6道工序被转移到M5数控卧车上进行加工。
生产中发生异常进行动态排程的甘特图如图5所示。
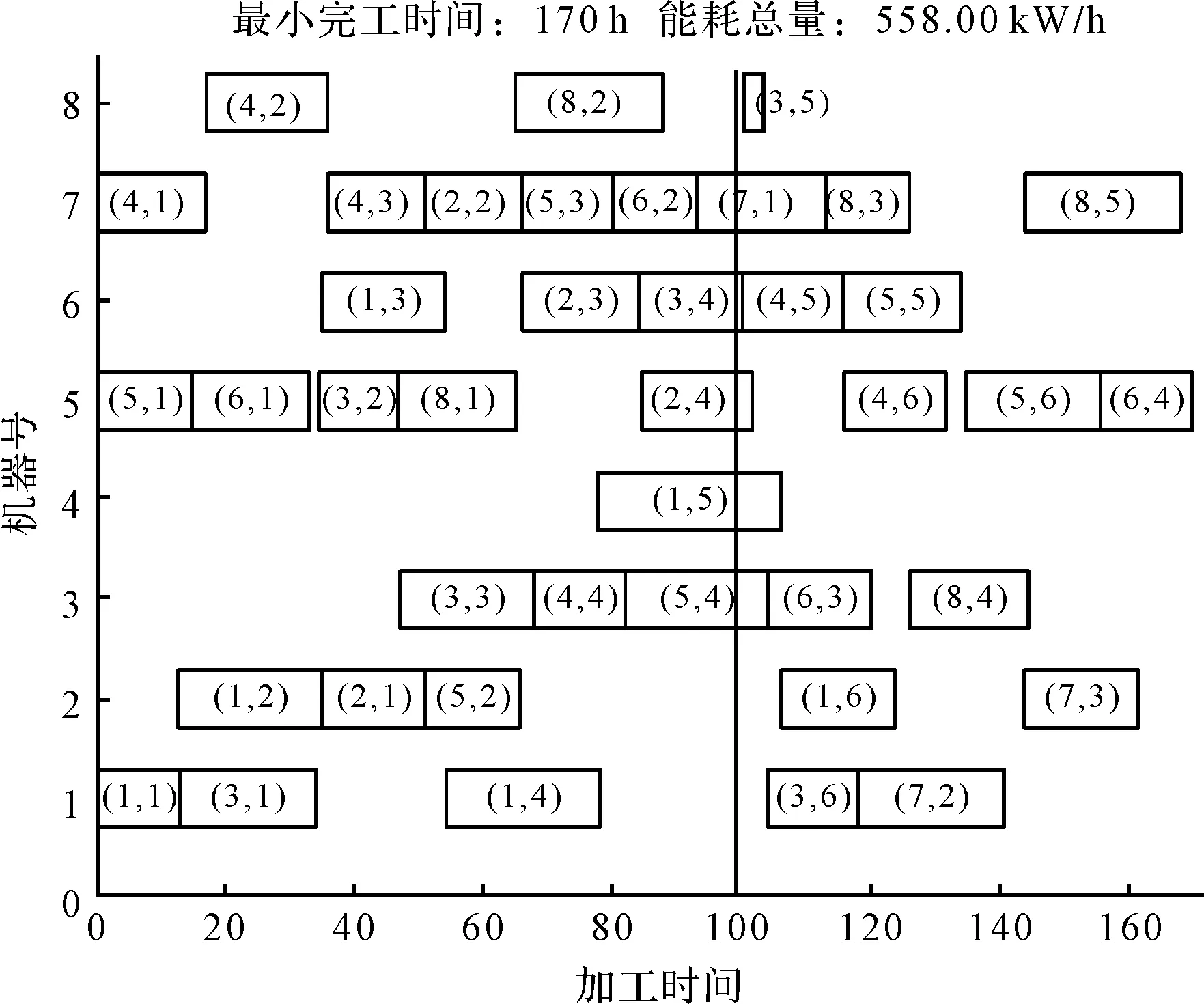
图5 生产中发生异常进行动态排程的甘特图
生产中发生异常的集合如表5所示。

表5 生产中发生异常的集合
根据该重型机械产品实际生产的完工时间和能耗量,测试本文提出方法的有效性。试验结果表明,本文提出的方法在考虑异常因素条件下,利用非支配排序遗传算法能够实时响应车间发生的异常情况,经对比,该方法能够提高生产计划制订效率20%以上。
5 结束语
机械加工作业车间异常情况发生后,生产将无法按原计划实施,通过相应的规则实时调整生产计划是决策者的首选。因此,快速响应需求且具有智能决策功能的机械加工生产作业排程是需要解决的重要难题。
本文在考虑生产实际中异常因素的基础上提出了动态排程规则,以最小完工时间、最低能耗量为优化目标,综合考虑工序及设备等约束,建立了优化模型,利用非支配遗传算法进行了多次迭代。
研究结果表明:
(1)水泥回转窑的实际生产与仿真结果一致,表明本文方法能够快速响应企业实际生产过程中发生的异常情况;
(2)本文方法能够辅助调度者快速对生产计划进行调整,经实际对比分析,该方法能够提高生产计划制订效率20%以上;
(3)通过仿真验证,表明本文方法响应速度快,结果准确度高、可靠性强,能够在实际生产当中使用。
本文仅研究了机械加工生产过程中面对异常因素的排程问题,未来将对装配过程中面对异常因素的排程进行研究。

