连续材料模型焊接接头裂尖力学场分析

陶晓庆，薛 河，王振文

(1.陕西能源职业技术学院实践教学管理处，陕西 咸阳 712000)

(2.西安科技大学机械工程学院，陕西 西安 710054)

(3.施耐德电气(中国)有限公司，北京 100102)

焊接接头的材料力学性能会因焊接时包括局部冶炼、铸造及热处理在内的流程处理而具有不均匀性[1]。焊接接头区域通常包括焊缝金属(weld metal，WM)、母材金属(base metal，BM)及熔合区(fusion zone，FZ)和热影响区(heat affected zone，HAZ)，各部分材料的力学性能都不尽相同，这给焊接接头断裂问题的研究带来了不少困难[2]。文献[1]通过等效屈服强度和加工硬化指数概念将焊接接头热影响区看作不同力学性能的不同组织进行分析。文献[3]、[4]在将焊接接头简化成只有母材和焊缝金属的“双材料”结构的基础上，将熔合区和热影响区简化成热熔区(heat fusion zone, HFZ)，形成了“理想三材料”模型，并分析了热影响力学性能及几何尺寸对非匹配焊接接头热影响区裂纹启裂的影响。文献[5]在将焊接接头简化为上述“理想三材料”结构基础上，进一步对裂纹进行分析。虽然已经有了较多基于这种“理想三材料”结构模型的焊接接头界面裂纹研究结果[6]，但这种简化模型在各区域的交界面变化过大，会极大降低分析的有效性。焊接接头虽然常被划分为材料力学性能不同的区域，但彼此之间并没有明显的界线，其材料力学性能的变化是连续的。对焊接接头的断裂问题进行更精确的研究，首先要建立更符合实际的焊接接头模型，因此本文针对以往研究中焊接接头模型存在材料力学性能突变的缺点，借助有限元分析软件建立材料力学性能连续变化的焊接接头模型，对断裂问题进行分析。

1 材料力学性能连续变化焊接接头模型建立

焊接接头的组成结构如图1所示。为了建立材料力学性能连续变化的焊接接头模型，需要依据焊接接头硬度分布来确定焊接接头不同区域的材料力学性能。

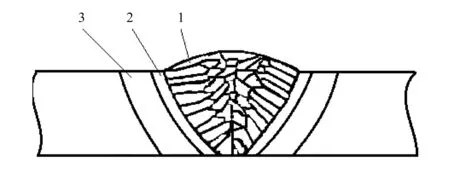
1—WM；2—FZ；3—HAZ

其具体步骤为：

1)硬度分布规律获取。使用微观硬度测试仪测量得到焊接接头的硬度分布。

2)硬度分布规律分析。焊接接头材料硬度与材料屈服应力呈线性关系，根据实验结果进行线性拟合，从而得到焊接接头区域的屈服硬度分布规律。

3)其他参数分布规律计算。通过计算确定焊接接头材料力学性能的其他参数分布规律。

4)建立接头模型。通过有限元分析软件建立材料力学性能连续变化的焊接接头模型。

1.1 焊接接头微观硬度测量

实验采用日本岛津公司HMV微硬度测试仪作为实验仪器，以25 g载荷量对焊接接头持续加载15 s，沿垂直于熔合线方向打硬度点，由于熔合区硬度变化较大，因此越靠近熔合线界面附近间隔越小，测试结果如图2所示。

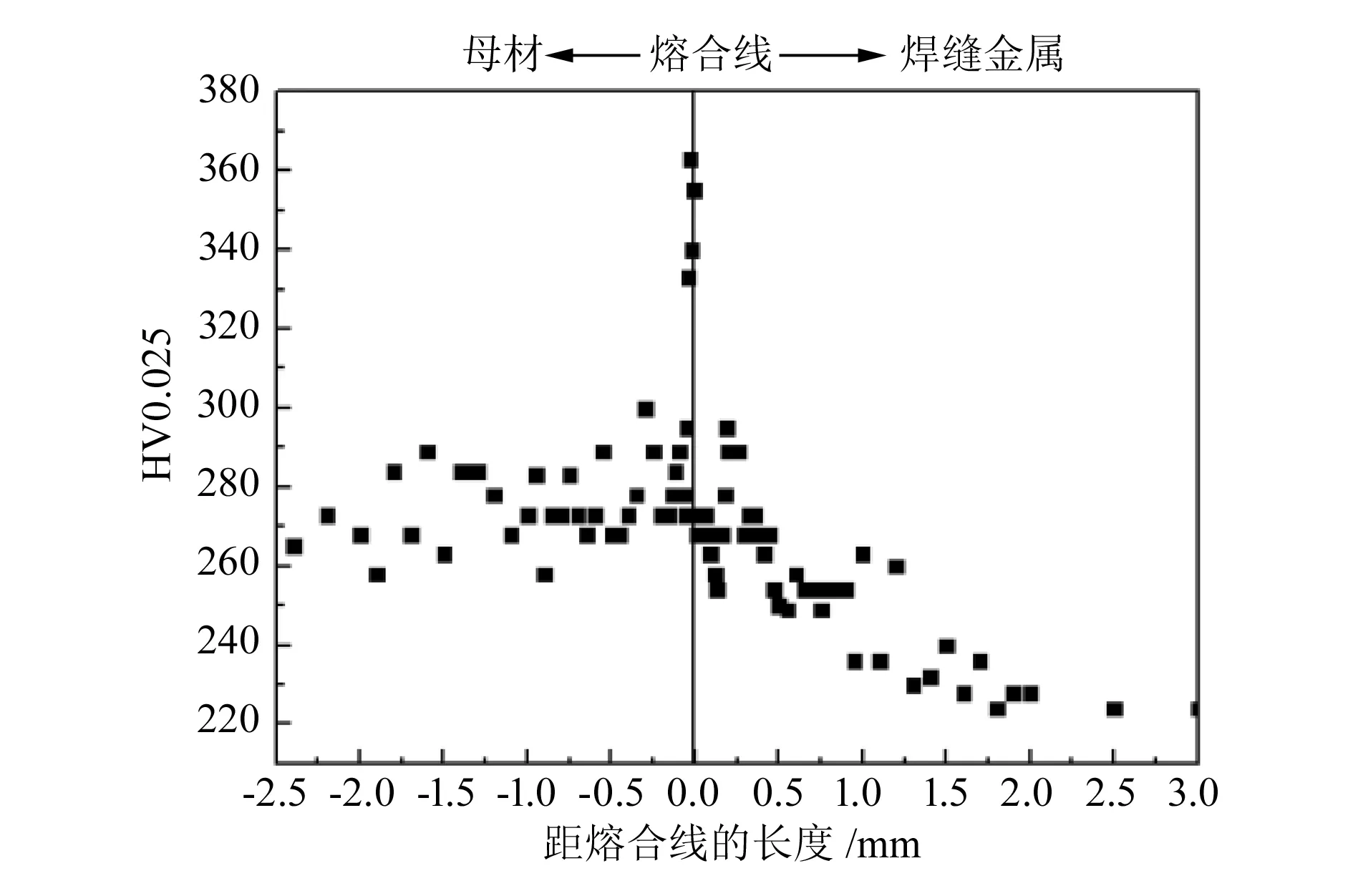
图2 焊接接头硬度测试图

1.2 焊接接头材料力学性能参数的确定

对于焊接接头这种“理想三材料”结构，不同区域的屈服强度及应变硬化指数不同，对应的材料力学性能也不一致。这种不一致性是影响裂纹扩展驱动力、断裂韧性和材料延性断裂行为的主要因素。

研究表明，材料的硬度与其屈服强度有关。根据图2可知，散点近似连成一条线，焊接接头硬度与其屈服强度呈线性关系，通过对焊接接头硬度测量能计算出焊接接头不同区域材料的屈服强度。

进一步的研究表明，应变硬化指数n与屈服应力σ0的关系可用式(1)表达：

(1)

式中：k为常数，取0.163。

为了便于分析裂尖断裂参量与材料力学性能的关系，对焊接接头硬度分布进行拟合，以熔合线为中心拟合公式如式(2)所示：

σ0=-16.994x2-2.5x+578

(2)

式中：x为裂纹位置。

材料力学性能符合Ramberg-Osgood关系。通过实验和计算可得焊接接头的屈服应力和硬化指数等具体参数，见表1。

表1 材料性能参数

1.3 试样和裂纹选取

本文研究的试样为GB 4161—84标准紧凑拉伸试样(1T-CT)，其几何尺寸和实验过程符合ASTM399标准[7-8]。试样的总体几何形状及尺寸如图3所示。

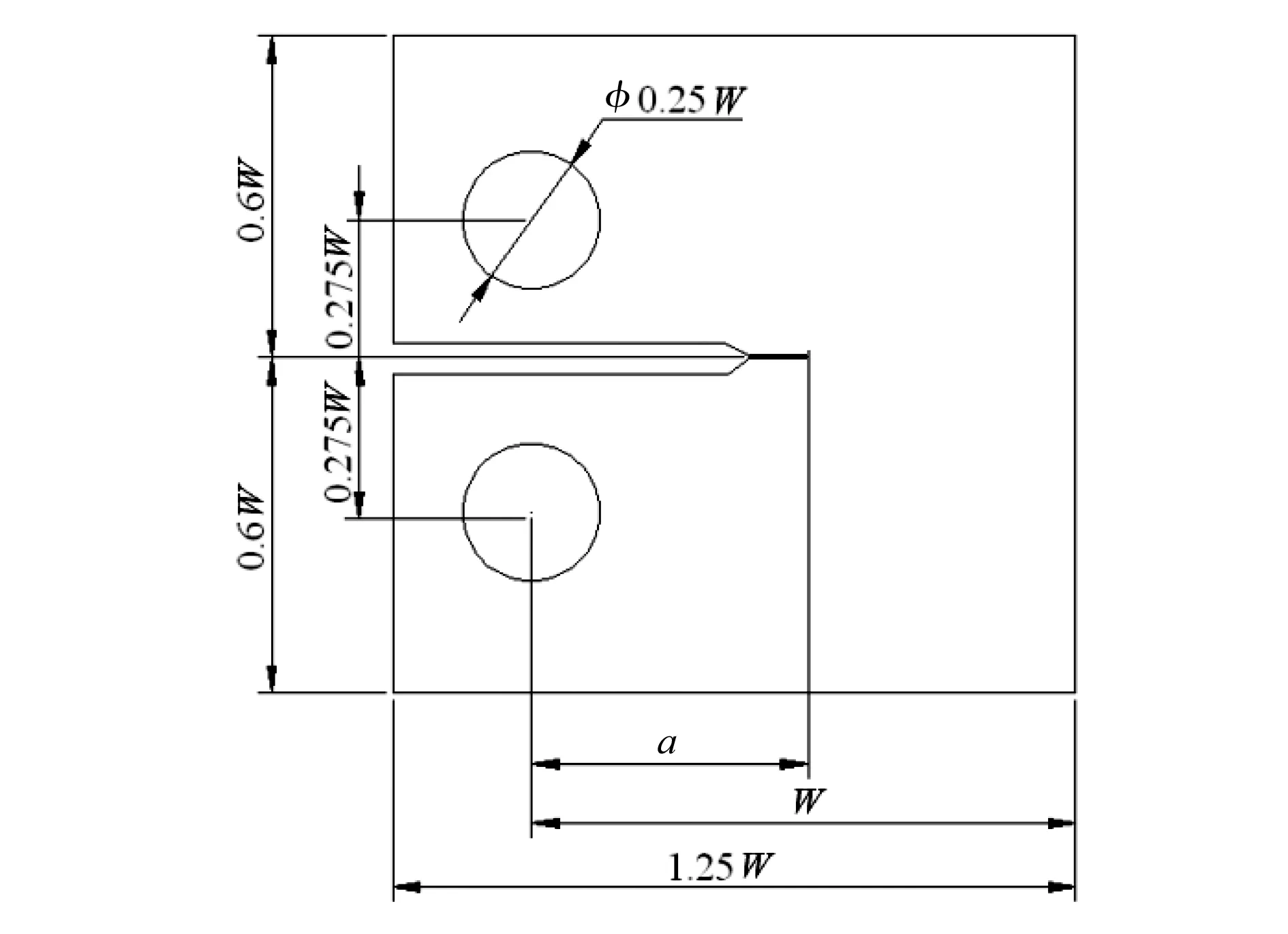
图3 试样的总体几何形状及尺寸

裂纹分布如图4(a)所示，以熔合线(图中粗线所示)为中心，在两侧位置X分别为0.2，0.4，0.6，0.8，1.0，2.0，3.0，4.0，5.0 mm处预制裂纹FB。

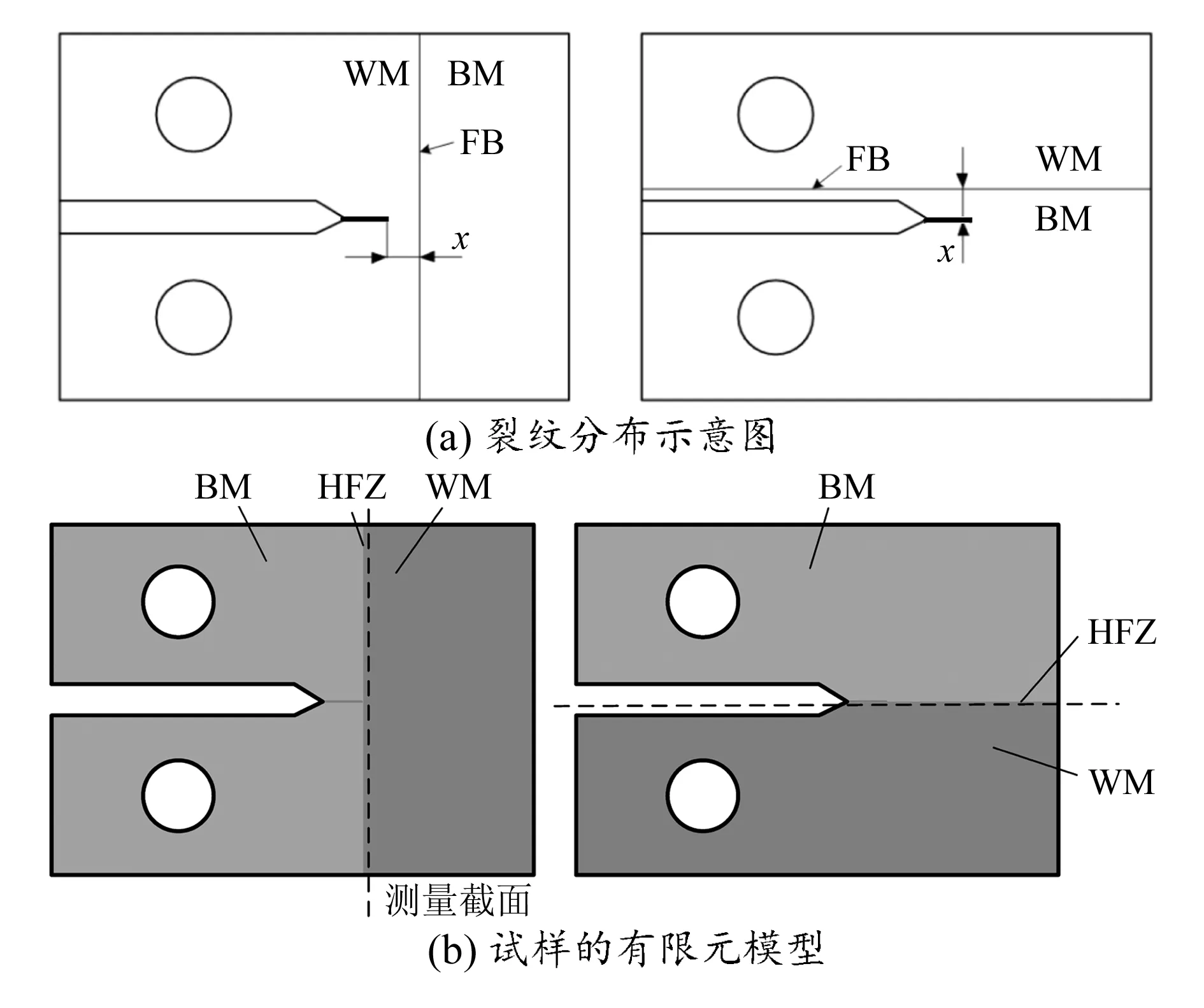
图4 试样的裂纹分布及有限元模型

1.4 接头模型的建立

接头的有限元模型如图4(b)所示，由于模型具有对称性，因此有限元模型取1/2模型，利用有限元软件对CT试样进行拉伸模拟，产生图4(a)所示方向的裂纹，并对其裂纹扩展驱动力参量进行计算。通过ABAQUS中的预定义场功能将表1中的材料力学属性加载到有限元模型中，实现了材料的力学性能参数连续变化的要求，其参数见表2。对模型完成有限元网格划分后共有23 568个单元。

表2 有限元模型参数

2 结果分析

为准确分析焊接接头裂尖力学场，需要减小其他因素的干扰，因此实验时对试样施加恒载K，并使其远离裂尖场。同时，为体现规律性，裂尖塑性区域需有足够大的范围。本实验令K=70.2 MPa·m1/2，同时分析纵向和横向裂纹状况。

模型中使裂纹尖端均匀分布于熔合线两侧-6～6 mm。在距离裂尖r=0.02 mm处(如图4(b)中虚线所示)采样，测量其应力应变的值并进行曲线分析。

图5、图6所示分别为有限元模型下纵向、横向界面裂纹裂尖应力应变云图，云图大小为1 mm×1 mm。

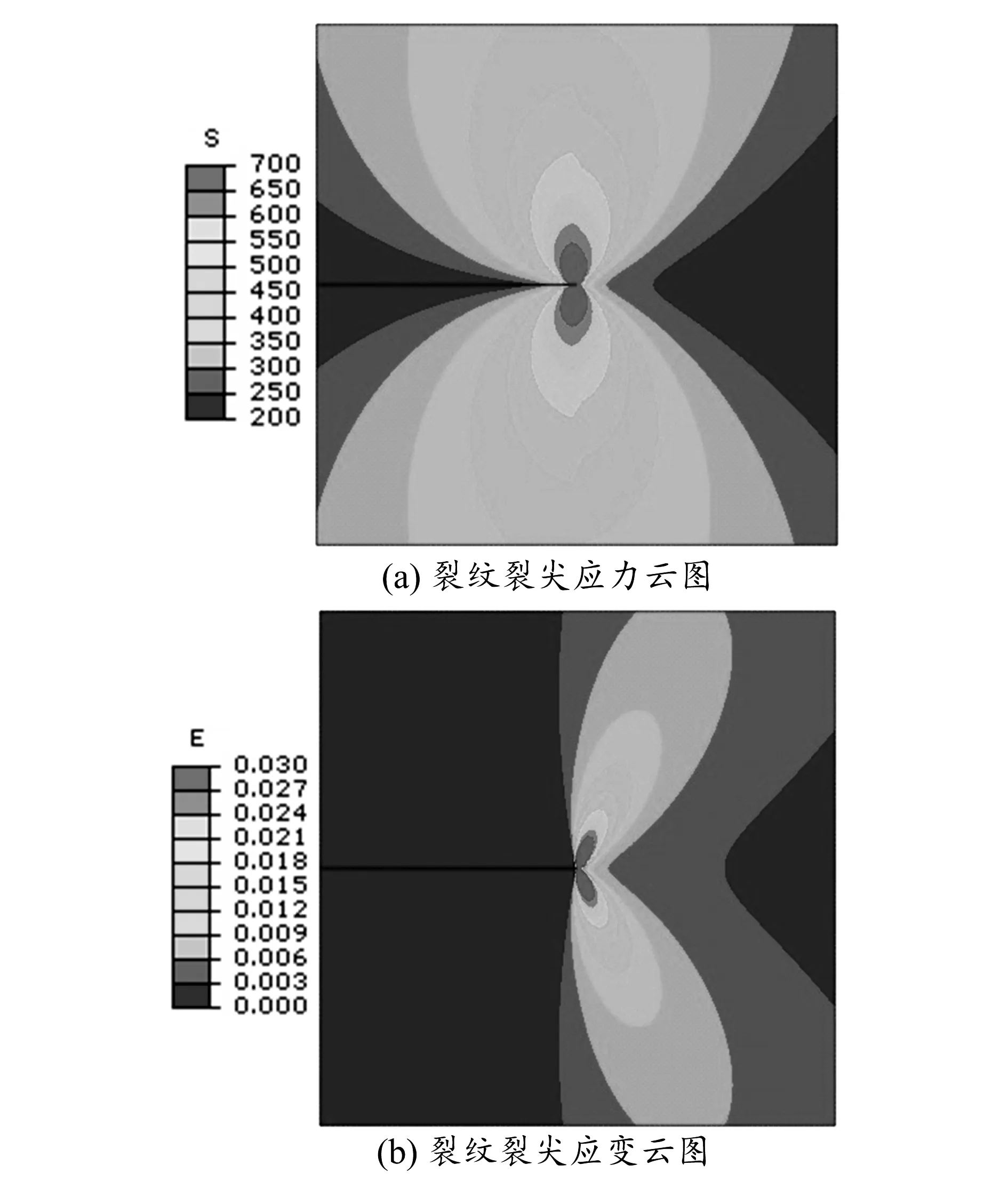
图6 有限元模型下横向界面裂纹裂尖应力应变云图

根据云图对纵向和横向裂纹裂尖应力应变分析,结果如图7、图8所示。其中MM是按照焊接接头最大屈服强度定义材料属性来计算得出的裂纹尖端应力属性变化，SM为“理想三材料”模型材料属性下裂纹尖端应力应变，CM为连续材料模型下裂纹尖端应力应变。

分析图7、图8可知，单一材料力学模型应力应变不变化，“理想三材料”材料力学模型下熔合线附近应力应变均产生了突变现象，而连续变化材料力学模型为连续过渡。图7，8中CM曲线和材料硬度分布曲线相似。不论是连续材料模型亦或“理想三材料”模型，其数值均在最小和最大屈服应力及单一材料的屈服应力之间。

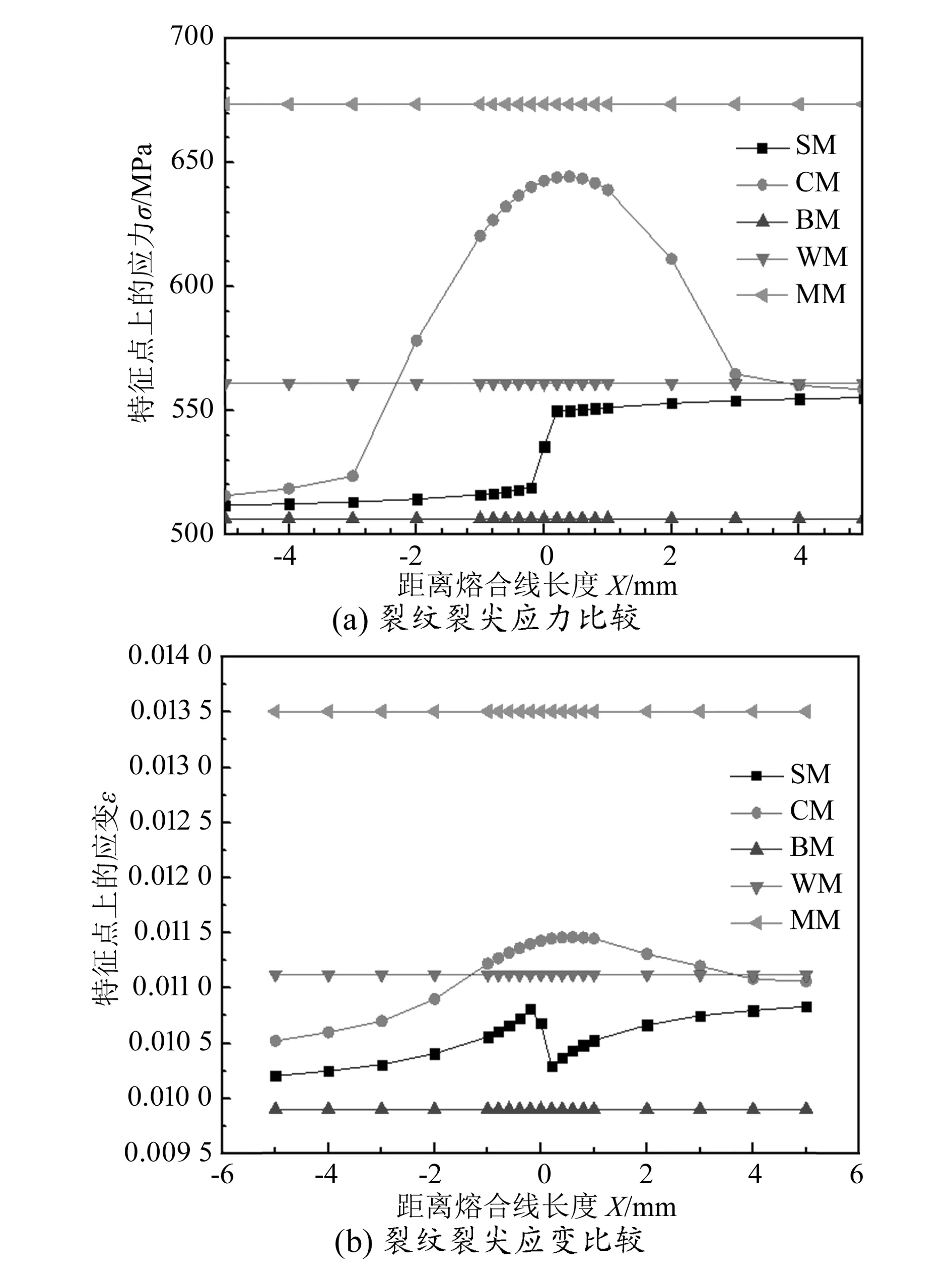
图7 不同模型纵向裂纹裂尖应力应变比较

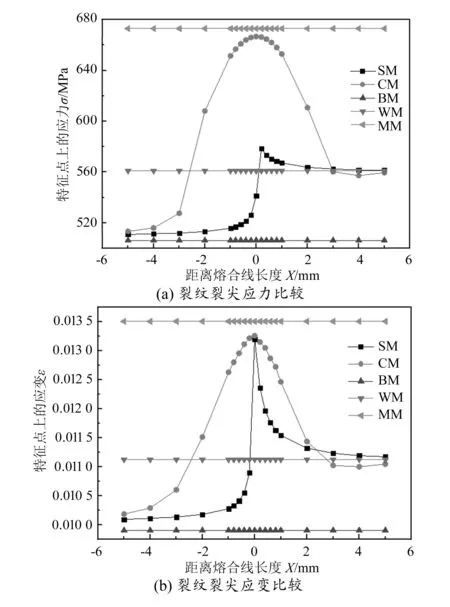
图8 不同模型横向裂纹裂尖应力应变比较

比较图7和图8可以看出，对于不同形式的裂纹，单一材料力学模型裂纹裂尖应力应变曲线基本一致；连续变化材料力学模型裂纹裂尖应力应变曲线变化规律相同；“理想三材料”材料力学模型裂纹裂尖应力应变曲线的规律则不同。由此说明，利用“理想三材料”材料力学模型来分析裂尖力学场时要考虑裂纹与焊缝的相互位置。

3 结论

本文通过对连续变化材料力学模型裂尖力学场的计算并与现有材料力学模型相比较，可以得到如下结论：

1)连续变化材料裂尖力学场与焊接接头硬度分布有关，变化趋势一致。其结果介于两者单一材料模型与“理想三材料”模型之间，说明了模型计算结果的有效性。

2)应用“理想三材料”材料力学模型对界面裂纹裂尖力学场进行分析计算时，应考虑分析对象与焊缝的相对位置，而连续变化材料力学模型无需考虑相对位置即可进行计算。