C70铁路敞车车体强度仿真及可靠性分析

马思群，孙雅琪，李 健，苏 航，王涛涛

(1.大连交通大学机车车辆工程学院，辽宁 大连 116028)

(2.大连交通大学网络信息中心，辽宁 大连 116028)

随着时代和科学技术的飞速发展，人们对于铁路机车车辆的性能指标、运用和维护的可靠性提出了越来越高的要求，而产品的可靠性直接影响其工作效率[1]。 车体是铁路货车实现货物运输的核心部件，它直接承受着来自货物的各种载荷，为了更安全、高效地实现货物的运输，有必要对其进行可靠性评估[2-3]。

C70型通用敞车是我国为了适应运输的多种要求而设计的多用途敞车，主要用来运输木材、煤炭、车辆、货柜等货物，载重70 t的C70敞车的投入运行极大地提高了我国铁路运输货物的能力[4]。

某公司在开发C70型敞车初期，仅以同类车型的基本参数为参考，没有考虑板材加工过程中板材厚度变化和使用过程中板材厚度的磨损、车身载荷的复杂性、实际制造过程中材料属性的多样性等因素的影响，实际上这些因素变化符合一定的分布规律。有鉴于此，本文首先建立了车辆几何模型(为减少计算规模，本文以半车模型为计算对象)，根据TB/T 1335—1996标准计算不同条件下车体静强度；然后通过ANSYS软件，采用蒙特卡罗法对车体进行了可靠性及灵敏度分析。

1 车体的静强度分析

1.1 车体施加的载荷说明

C70型敞车车体的主要材料为Q450钢，其屈服强度为450 MPa，取许用安全系数为1.2，通过计算可得许用应力值为375 MPa。

1)垂向载荷。

①垂向静载荷Pj。

Pj=(车辆载重+车辆自重-转向架质量×2)×9 800=787 920 (N)

半车的垂向静载荷=787 920/2=393 960(N)

②垂向动载荷系数Kd。

(1)

式中：fj为车辆在垂向静载荷下的弹簧静挠度；v为车辆的设计速度；a,b,c,d为系数。

已知，fj=42.8 mm，v=120 km/h，a=1.5,b=0.05,c=0.427,d=1.65,计算可得Kd=0.283。

③垂向总载荷Pd。

Pd=Pj×(1+Kd)

(2)

代入数据得Pd=1.01×106N。

2)纵向载荷。

根据标准TB/T 1335—1996《铁道车辆强度设计及试验鉴定规范》，C70铁路货车各个工况下施加的纵向载荷取值如下：

第一工况拉伸力，纵向载荷为1 125 000 N；第一工况压缩力，纵向载荷为1 400 000 N；第二工况压缩力，纵向载荷为2 250 000 N。

3)侧向力。

车体施加的侧向力与垂向载荷有关，垂向静载荷的10%即侧向力为78 792 N。

1.2 敞车车体载荷组合工况

结合敞车在运行过程中车体的真实状态与强度标准，把经计算所得的各种载荷分别施加在车身上。各个计算工况的情况说明如下。

工况一：垂向总载荷+1 125 000 N纵向拉伸力+侧向力。

垂向总载荷作用在车体底架上，此外还要考虑风载作用下的侧向力，垂向总载荷为1.01×106N，侧向力为78 792 N，因此施加在车体底架上的载荷为1.09×106N。强度计算基于1/2 车身模型，因此应用于底架的负载应为总负载的一半，为544 396 N。等效后的垂向力平均施加在车底板的每个节点上，经统计所作用的节点共有48 112个，每个节点所受垂向力为11.32 N。1 125 000 N纵向拉伸力取其一半加载到前从板座节点上。前从板座一共有204个节点，每个节点所受到的拉伸力为27 575.98 N。

工况二：垂向总载荷+1 400 000 N纵向压缩力+侧向力。

在车体底架上施加的垂向总载荷和侧向力形成的等效垂向载荷与工况一相同。将纵向压缩力1 400 000 N的一半施加在车辆两端的后从板座上。后从板座一共有280个节点，每个节点所受到的拉伸力为2 500 N。

工况三：垂向静载荷+2 250 000 N纵向压缩力。

垂向静载荷787 920 N的一半393 960 N作用在车体底架的节点上，平均分布在每个节点上的力为8.33 N，纵向压缩力2 250 000 N值的一半1 125 000 N作用在沿车钩中心线车辆两端的后从板座节点上。后从板座一共有260个节点，每个节点所受到的拉伸力为4 326.92 N。

工况四：垂向静载荷。

垂向静载荷作用在车体底架的节点上，由于所用的模型为1/2车体模型，所以施加垂向静载荷的一半，平均分布在每个节点上的力为8.33 N。

4种计算工况汇总见表1。

表1 计算工况汇总表

1.3 车体有限元模型建立

首先在SolidWorks中建立几何模型，接着在Hypermesh中建立车体的有限元模型，为提高网格的质量，对某些部位进行了简化。C70型敞车车体模型划分时采用的是三节点三角形网格和四节点四边形网格两种混合型网格，为了保证其精确度，划分模型时采用大小为20 mm的有限元网格。车体的节点总数为212 935个，单元总数为218 235个。车体有限元模型如图1所示。加载、约束、定义属性等工作完成后，导入ANSYS进行静强度计算。

图1 车体有限元模型

1.4 静态强度的结果分析。

在ANSYS中，对上述4种工况进行了分析和计算。在评估结构的静态强度时，使用第四强度理论:

(3)

式中:σs为材料的等效应力;σ1,σ2,σ3分别为第一、第二、第三主应力。

通过计算可得不同工况下强度结果，限于篇幅，仅列出工况二的最大应力整体图，如图2所示。4种工况下车体强度计算结果见表2。

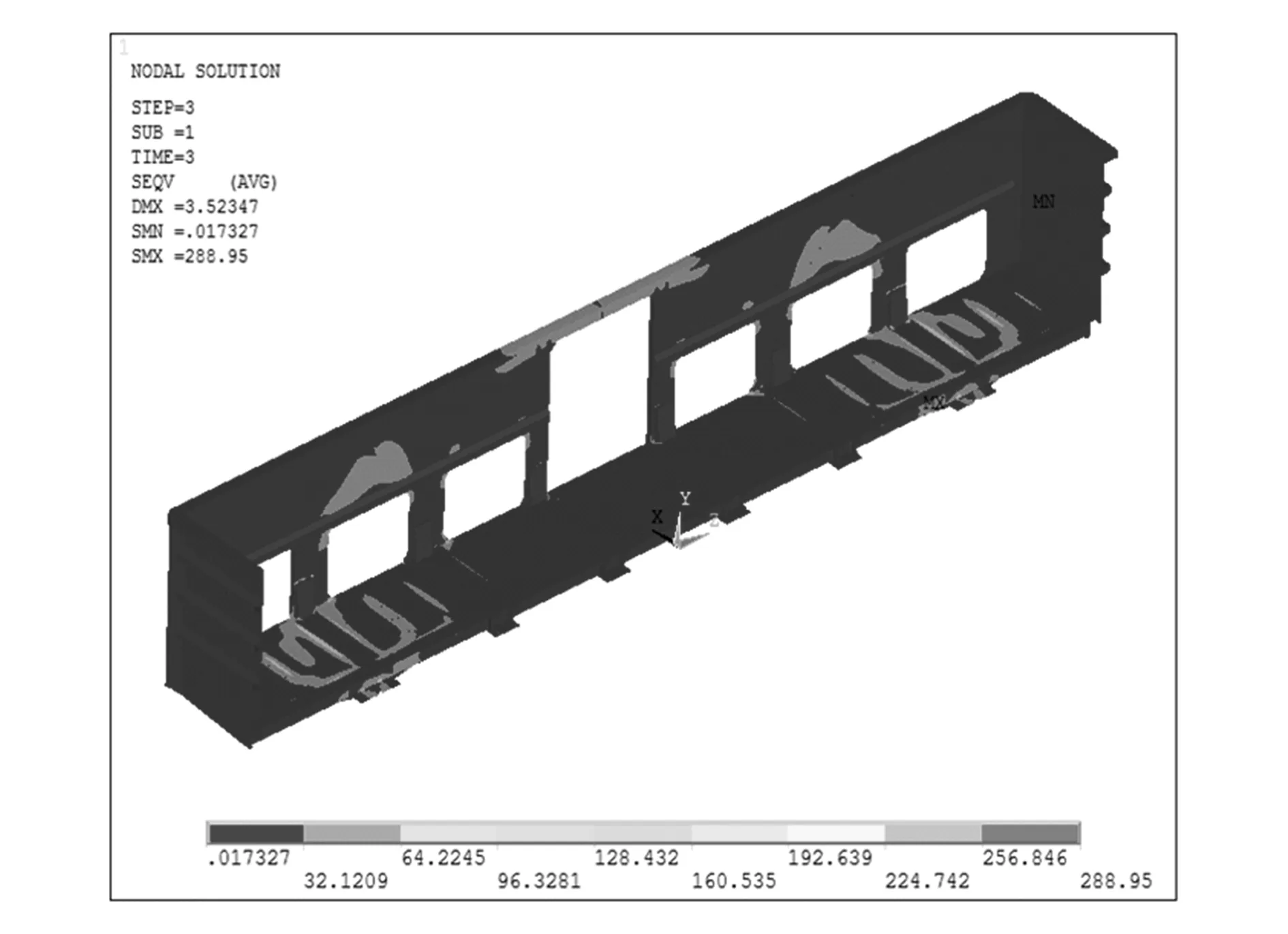
图2 工况二下的整体应力图

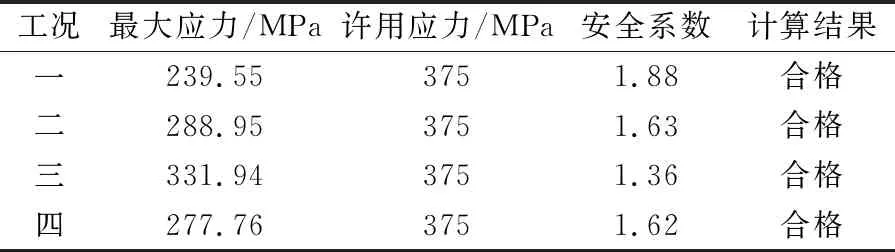
表2 4种工况下车体强度计算结果

1.5 模态分析

将有限元模型导入ANSYS中进行模态计算，使用软件中默认计算结果提取方法(Block Lanczos)方法，计算的模态为自由模态，计算结果中前6阶模态为刚体模态，限于篇幅，仅列出第8阶模态下的位移变形如图3所示，模态计算结果见表3。

图3 8阶模态下的位移变形图

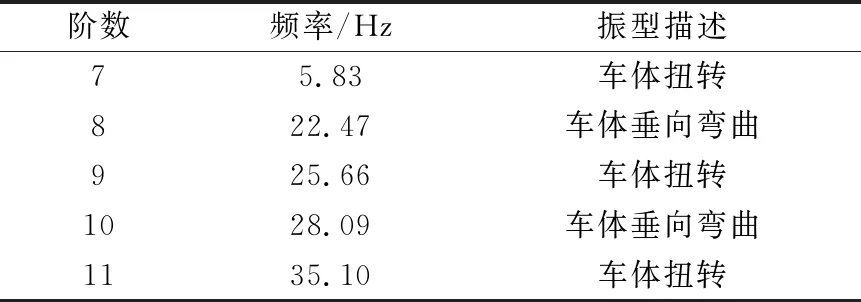
表3 模态计算频率

2 基于ANSYS/PDS的可靠性分析

2.1 车体可靠性以及灵敏度分析步骤

1)建立概率分析文件。首先建立几何模型，在Hypermesh软件中对模型进行加载、约束等，并导出 cdb 文件，然后对其进行定义输入、输出变量等，最后得到mac文件。

2)进行可靠性分析。在ANSYS中导入mac文件，对变量进行设置，接着选择蒙特卡罗法作为分析方法、拉丁超立方抽样法作为抽样方法，设定300次为抽样次数。

3)结果后处理。提取历史样本、灵敏度结果分析图等[5-6]。通过灵敏度结果分析图可知，许用应力对结构的影响最大。

2.2 车体极限状态方程的建立

极限状态方程在可靠性分析中起着非常重要的作用，根据应力强度干涉理论，车体的极限状态方程可定义为:

Z=g(x1,x2,…,xn)=[σ]-[σmax]

(4)

式中：Z为状态函数；x1,x2,…,xn为随机变量；[σ]为材料许用应力；[σmax]为车体最大等效应力。

极限状态方程的3种情况如下：Z>0，车体处于安全状态;Z=0，车体处于极限状态;Z<0，车体处于失效状态。

结合弹性模量、载重、泊松比等随机变量的分布特征，分析Z≥0的概率分布特征，进一步分析各设计参数对车辆节点最大等效应力的影响程度。

2.3 车体随机变量的确定

随机变量分为随机输入变量和随机输出变量。

1)车体载荷随机输入变量的确定。

车体载荷的变化符合高斯分布，车体载荷可从可靠性数据获得。静态强度计算结果表明，垂向载荷对车身应力分布有很大影响[7]。本文选择工况三下的垂向载荷，变异系数为 0.05。

2)车体材料属性随机输入变量的确定。

车体材料属性的变化符合高斯分布，可以通过可靠性资料得出。弹性模量和许用应力被选为随机输入变量，选择材料属性中的标准值，变异系数为 0.05。

3)车体几何随机输入变量的确定。

在车身加工过程中和车辆投入使用后长时间的磨损过程中，车身板厚发生变化。车身板厚分布类型为均匀分布，误差不超过±1 mm。考虑到枕梁上侧盖板和主盖板的厚度变化，对其应力影响较大，所以将其列入随机输入变量中。输入随机变量及其分布见表4。

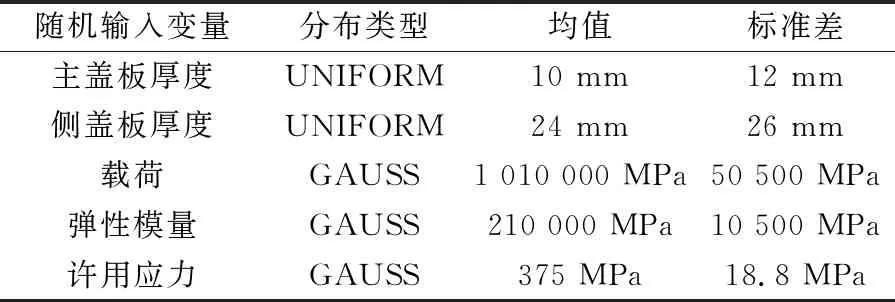
表4 随机输入变量及其分布

2.4 车体的可靠性分析

1)在PDS模块中，设置了随机变量的均值、标准差和分布类型，将车身的最大等效应力作为输出变量，获得历史样本、灵敏度分析图等。

2)通过车体极限状态方程的历史样本可得Z值较大且都大于0，如图4所示。此外，在PDS模块的后处理分析中，可以计算大于0的极限状态方程的概率，从95%的置信度计算概率信息，获得车体的可靠度为100%。

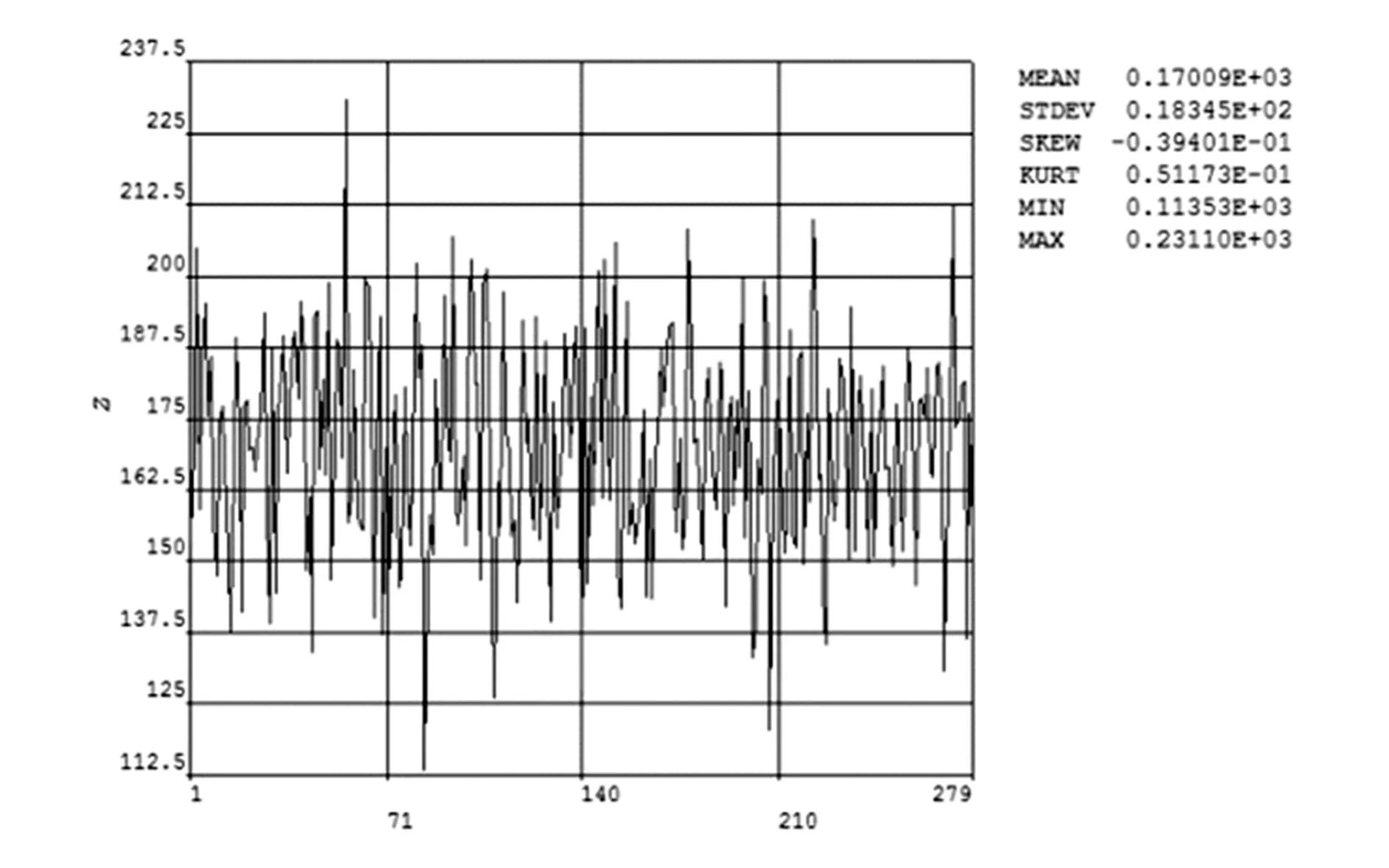
图4 Z的历史样本

3)设定一定置信度后，可靠性灵敏度分析结果如图5所示，由饼状图可知：许用应力对车身的静态强度可靠性影响最大。从柱状图可以看出，弹性模量、旁侧盖板的厚度、垂向载荷、主盖板的厚度为负值，即与静态强度可靠性呈负相关，车体的等效应力是随着弹性模量、旁侧盖板的厚度、主盖板的厚度、垂向载荷的增大而增大。应力与车身静态强度的可靠性呈正相关，应力值越高，车身越安全可靠。

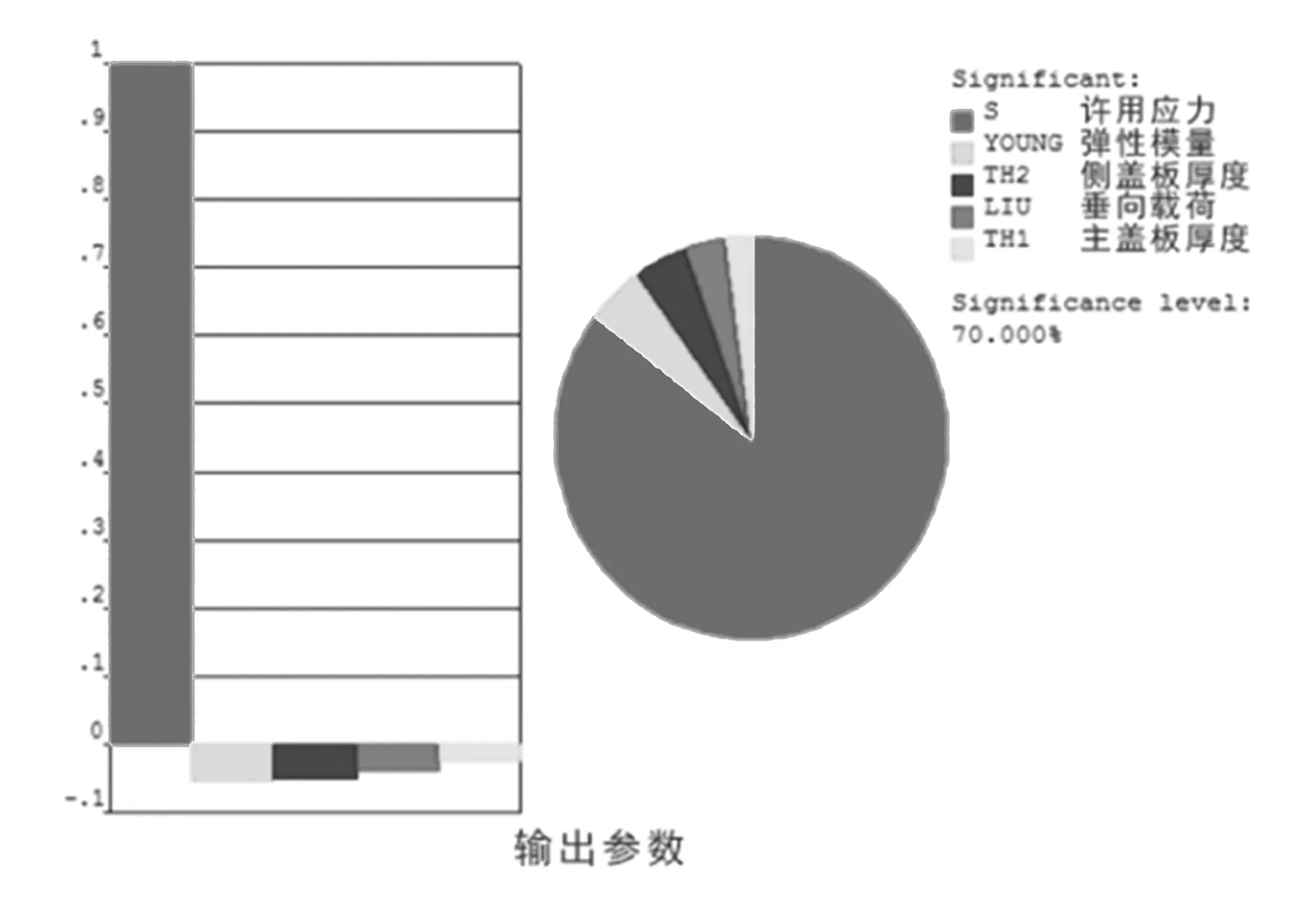
图5 灵敏度分析图

3 结论

1)由TB/T 1335—1996加载标准可以得出，4种计算工况中，工况三等效应力最大，并且满足标准要求。

2)模型在频域上的表现正常。

3)通过极限状态方程的历史样本可以得出Z值较大且都大于0，车体的可靠度为100%。

4)灵敏度分析结果表明，车辆的许用应力对车身的可靠性影响最大，弹性模量、旁侧盖板的厚度、垂向载荷、主盖板的厚度对车体静强度可靠性的影响较小。在该模型车体的设计中，可以参考分析结果，合理选择车身板材，使车身的垂向载荷尽可能在允许的范围内，以确保列车的安全、可靠运行。