基于改进粒子群算法的列车速度跟踪自抗扰控制器设计

杨 杰，陈昱圻，王盼盼

(1.江西理工大学 永磁磁浮技术与轨道交通研究院，江西 赣州 341000；2.江西省磁悬浮技术重点实验室，江西 赣州 341000)

随着我国铁路事业的快速发展，传统轮轨交通运输在安全、绿色、智能化控制层面具有了更高层次的要求，与此同时，相应的列车自动驾驶控制策略也需要不断地改进与完善。其中，列车速度跟踪控制作为列车自动运行系统(Automatic Train Operation, ATO)的核心模块，如何最大限度保障列车运行状态，依然具有研究意义[1]。截至2020年7月底，我国铁路营业里程突破14万km，其中高铁3.6万km[2]，这也意味着列车速度跟踪控制研究具备庞大的市场应用需求和研究价值。

在列车速度跟踪控制问题方面，国内外研究成果相对较多，为本文提供了良好的参考价值。针对列车控制目标速度曲线优化的瓶颈，杨杰等[3]融合了数学推理、逻辑分析和软件仿真等优势，提出一种全新节能运行优化算法，实现了复杂线路下列车的高效优化。同年，贾利民等[4]提出了多模态模糊PID控制算法(MMFPID)，采用牵引力前馈和局部输出限幅方法，较好地提升了控制器的动态性能，实现了列车速度目标曲线的快速精准跟踪。针对高速车自动驾驶系统精确进站停车问题，何之煜等[5]设计一种自适应模糊滑模控制器，可以柔化非线性切换控制信号，实现精确停车。Chang等[6]提出基于差分进化算法的模糊控制器站间运行调整算法，并通过对基本差分进化算法的改进实现对系统的准时性、舒适性和节能性的多目标优化。Dong等[7]针对不同工作条件，根据模糊规则和预测方法进行调整，以减少时间延迟并提高运输效率。

基于经典PID的误差反馈处理的控制思想，韩京清[8]提出了自抗扰控制算法(Active Disturbance Rejection Controller,ADRC)。其中，自抗扰算法的精髓在于对跟踪微分器、非线性状态误差反馈控制律和扩张状态观测器的设计与优化。目前，自抗扰控制已有二十多年的发展历程，受到了国内外学者的广泛关注与研究。龙志强等[9]以磁浮列车为控制对象，利用自抗扰控制算法进行自动驾驶控制，研究了自抗扰控制算法对磁浮列车运行控制系统的适应性。楚东来[10]利用改进的粒子群算法(Particle Swarm Optimization, PSO)，对自抗扰控制参数进行优化设计。李诚等[11]提出一种基于动态邻居和广义学习策略的粒子群优化全局控制策略的算法，获得在列车安全运行的前提下，满足一定能耗、运行时间误差和停站误差要求的全局ATO控制策略。孟建军等[12]采用列车牵引计算知识建立列车运行多目标模型，并利用遗传算法对此模型进行优化，搭建预测模糊PID控制仿真模型，结果表明可以最大程度地提高列车停车精度。连文博等[13]采用单质点列车模型，令未知部分作为扩张状态设计二阶自抗扰控制器，验证了自抗扰控制下高速列车速度跟踪控制器具有抗干扰性强、追踪精度高等优势。针对列车时滞控制模型，Wang等[14]设计了非线性自抗扰控制器算法，并引入人工蜂群算法，有效解决了非线性自抗扰控制器算法参数难调整的问题。黄江平等[15]针对列车节能控制优化效果不明显、收敛速度慢等问题，提出一种引入自适应惯性权重，同时加入具有调整能力的动态学习因子与改进速度更新公式的粒子群优化算法，与传统的列车运行优化算法相比，改进后的优化算法收敛速度更快，列车节能效果更好。

针对货运列车速度跟踪控制问题，设计二阶非线性自抗扰控制器，并选择合适的适应度函数。针对自抗扰控制器参数多、整定难的问题，选用粒子群算法进行参数整定，采用改进惯性权重w的方法来改进粒子群算法，加快算法搜索速度。

1 货运列车的控制模型

采用单质点列车模型，以HXD3列车为例，研究机车的牵引和制动特性。模型表示如下

(1)

式中：x为列车运行距离；v为列车运行速度；F为列车所受合力；M为列车总质量；γ为车轮的转弯质量系数。

当列车处于不同的运行状态时，总力F表示为

(2)

式中：FtN为牵引力；w0为基本阻力；wj为与线路有关的附加阻力；FbN为制动力。

w0(v)和wj分别为

(3)

式中：ra为基准阻力参数；rb为滚动阻力参数；rc为空气阻力参数；g为重力加速度；wi为斜坡附加阻力，wr为弯道附加阻力；ws为隧道附加阻力。

列车的牵引和制动过程可以由具有传递延迟的一阶惯性系统的动力学方程表示。此外将系统的传输时间和响应延迟视为系统的内部干扰。列车牵引制动系统的传递函数G(s)为[16]

(4)

式中：s为复变量；T为牵引制动系统的传递延迟；τ为牵引制动系统的响应时间常数。

系统状态空间方程可以通过传递函数来求解

(5)

式中：f(x1，x2)为系统函数；b0为控制器参数；u为控制器输出控制量；d(t)为列车的内部干扰和外部干扰之和。

2 自抗扰控制器

将列车的基本阻力和附加阻力视为外部干扰，牵引和制动系统的响应时间和传递时间视为内部干扰，因此，列车控制系统模型可以看作是一个二阶系统。设计二阶非线性自抗扰控制器，如图1所示。

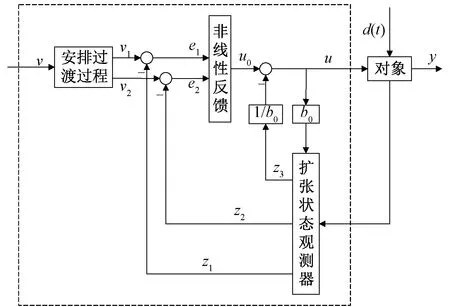
图1 二阶非线性自抗扰控制器

非线性自抗扰控制器由三个部分组成：跟踪微分器(Tracking Differentiator, TD)，扩张状态观测器(Extended State Observer, ESO)和非线性状态误差反馈控制律(Nonlinear State Error Feedback, NLSEF)。自抗扰控制器的3个重要模块可以根据不确定的非线性对象进行设计。

2.1 跟踪微分器

以二阶非线性自抗扰控制器为例，它的过渡过程是由非线性跟踪微分器完成，其离散形式为

(6)

式中：fh为定义变量；fhan(v1(k)-v(k),v2(k),r,h0)为最速控制综合函数；h为跟踪微分器的积分步长；h0为滤波因子；v(k)为列车目标速度曲线数据，作为跟踪微分器的输入，v1(k)与v2(k)为微分控制器的输出，并且v2(k)为v1(k)的微分；r为跟踪速度因子，在一定条件下，r越大，v1(k)跟踪v(k)的速度越快；。

函数fhan(x1,x2,r,h0)的计算方法为

(7)

式中：l为符号函数sign(·)的线性区间；l0，α0，α，y均为最速控制综合函数fhan(v1(k)-v(k),v2(k),r,h0)的中间变量。

2.2 扩张状态观测器

ESO是将被控系统的内部和外部干扰扩张到一个新的状态量，然后根据具体的误差反馈机制对系统扰动进行补偿。

(8)

式中：e为系统的输出误差；z1、z2分别为对速度、加速度的观测估计；z3为对系统总扰动的观测估计；y为跟踪速度的输出；b为控制对象参数；u为控制器输出；β01，β02，β03为ESO针对不同系统的可调参数；φi(e)为线性函数。

(9)

其中，fal为用户自定义函数。

β01、β02、β03表达式分别为

(10)

式中：w0为带宽。

2.3 非线性状态误差反馈控制律

NLSEF根据系统状态误差的非线性组合确定控制量，并用z3对反馈控制量u0进行补偿，得到控制量u(t)为

(11)

式中：e1为跟踪微分器的输出v1与扩张状态观测器的输出z1之差；e2为跟踪微分器的输出v2与扩张状态观测器的输出z2之差；kp为比例放大系数；kd为微分项系数。

(12)

3 改进粒子群ADRC参数优化设计

3.1 粒子群算法基本原理

PSO算法是计算智能领域的一种群体智能优化算法[17-18]。PSO算法具有精度高、收敛速度快、容易实现等优点。它与遗传算法相比，规则简单，没有遗传算法的“交叉”和“变异”操作，通过追随粒子当前搜索到的群体极值寻找全局最优。

在一个多维的搜索空间中，由n个粒子组成的种群X=(X1,X2,…,Xn)，第i个粒子Xi=(Xi1,Xi2,…,XiD)T表示当前粒子所在位置，作为问题的假设解。代入适应度函数计算出每个粒子位置Xi对应的适应度值。

每迭代一次，都要更新粒子的速度和位置，更新方法为

(13)

式中：d=1,2,…,D，D为参数个数；w为权重因子；k为当前迭代次数；Vi为粒子的速度，Vi=(Vi1,Vi2,…,ViD)T；Pi为粒子个体极值，表示为种群的群体极值为Pi=(Pi1,Pi2,…,PiD)T；Pg为种群当前极值，表示为Pg=(Pg1,Pg2,…,PgD)T。c1和c2均为正常数；r1和r2为(0,1)之间的随机数。并且将粒子的位置与速度分别限制在区间[Xmin,Xmax]、[Vmin,Vmax]之内。

选用ITAE指标作为适应度函数JITAE为

(14)

式中：e(t)为系统误差。

3.2 算法的改进

PSO算法虽然具有收敛速度快、容易实现等优点，但是有早熟收敛、后期容易陷入局部最优的缺点。通常以增强改进惯性权重和收敛因子、与其他进化算法相结合等方法改进。在基础PSO算法中，每一个粒子的权重因子w是常数，这就没有充分发挥优质粒子的搜索能力。通过计算当前粒子与群体最优粒子之间的距离来调节该粒子的惯性权重w，当两者之间的距离较大时，减小惯性权重w，反之，则增大惯性权重w。这样增大优质粒子的权重w，减小劣质粒子的权重w的方法对基础粒子群算法进行改进，能够适当减小算法陷入局部最优的概率，由于本文采用ADRC控制器，该控制器能够适应的对象参数范围很大，鲁棒性很强，而改变惯性权重w能够保证系统稳定的前提下最大程度上加快搜索速度。通过改变收敛因子与其他进化算法相结合等方法也能加快搜索速度，但是容易使系统不稳定。因此采用改进惯性权重w的方法，计算式为

(15)

式中：f为粒子实时的适应度函数值；favg、fmin分别为当前所有粒子的适应度函数值的平均值、最小值。

改进前后粒子群算法最优适应值对比见图2。

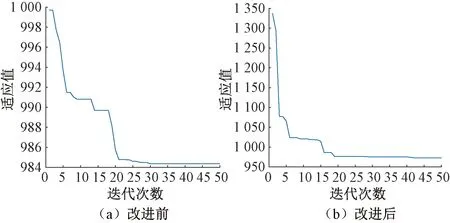
图2 改进前后粒子群算法最优适应值对比

由图2可知，与一般的粒子群算法相比，改进后的粒子群算法在15代左右就开始收敛得到最优适应值，而一般的粒子群算法在20代左右才开始收敛，这表明改进后的粒子群算法的运算效率得到提升。

3.3 改进PSO算法优化ADRC参数

采用改进粒子群算法来综合优秀的经验，自适应地调整ADRC控制器的参数，即b0、w0、kp、kd4个参数。在确定适应度函数后，就可以对参数进行寻优。在满足约束条件下，使适应度函数值最小时对应的参数即为最优控制器参数。算法具体步骤为

Step1初始化粒子群，确定种群规模、适应度函数、每个粒子的位置Xi和速度Vi。

Step2对自抗扰算法进行仿真，根据适应度函数计算各个粒子的适应度值。

Step3将粒子的适应度值与个体极值比较，并对个体极值更新。

Step4将粒子的适应度值与全局极值比较，并对全局极值更新。

Step5按照公式(13)更新每个粒子的位置与速度。

Step6按照公式(14)更新惯性系数。

Step7满足结束条件时，停止迭代并输出最优解，否则，返回Step2。

改进PSO算法优化ADRC控制器的过程示意见图3。

图3 改进PSO算法优化ADRC控制器过程示意

4 仿真分析

结合某型货运列车的实际数据及基础理论模型，设计基于自抗扰控制算法的货运列车速度跟踪控制系统，并以货运列车的实际运行数据计算出列车运行的目标速度曲线，对列车的运行轨迹进行模拟验证。在同等条件下，对比分析经典PID控制算法和基于人工蜂群算法-自抗扰智能控制策略的列车速度跟踪性能。

某型货运列车的具体参数见表1。

表1 某型货运列车参数

设计的Simulink模型包括：ADRC模型、牵引系统模型、阻力模型和列车速度响应模型。基于Matlab2020a的m文件和Simulink模型混合编程的列车控制仿真系统环境，总体结构见图4。

图4 列车控制仿真系统结构

采用文献[19]中所述的列车目标速度曲线作为第4节控制器的输入信号，见图5。

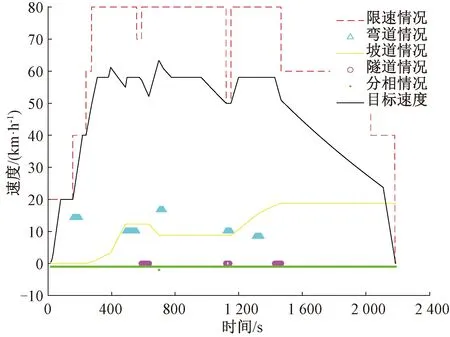
图5 列车目标速度曲线

4.1 仿真结果

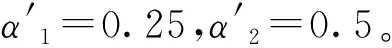
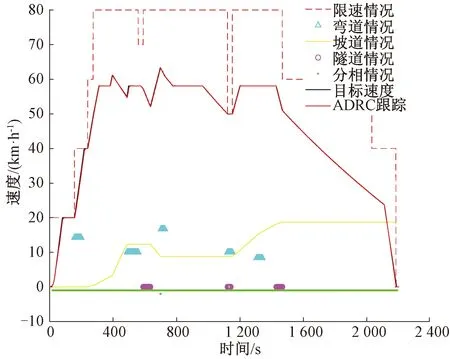
图6 改进PSO算法的ADRC控制器目标速度跟踪曲线

由图6可知，基于改进PSO算法的ADRC控制器的速度跟踪控制在启动、加速、匀速、制动模态中能够较好地对目标速度进行跟踪，即使线路空间包含陡坡，限速情况比较复杂，跟踪曲线也能几乎与目标速度吻合，没有出现超调现象。

通过改进PSO算法优化ADRC控制器得到的参数变化曲线见图7。

图7 参数优化曲线

由图7可知，参数b即优化参数b0在第3、8次迭代中发生改变，参数w即优化参数w0、kp、kd出现多次变化，反复迭代50次，最终得到最佳结果：b0=1，w0=6.142 1，kp=1.173 5，kd=1.837 2。由图2可知，在算法优化过程中，群体最优适应值不断减小，PSO算法不断寻找更优的参数，最终得到最优的4个参数值。

4.2 比较分析

将基于改进PSO算法与人工蜂群算法、经典PID控制算法进行比较，见图8。

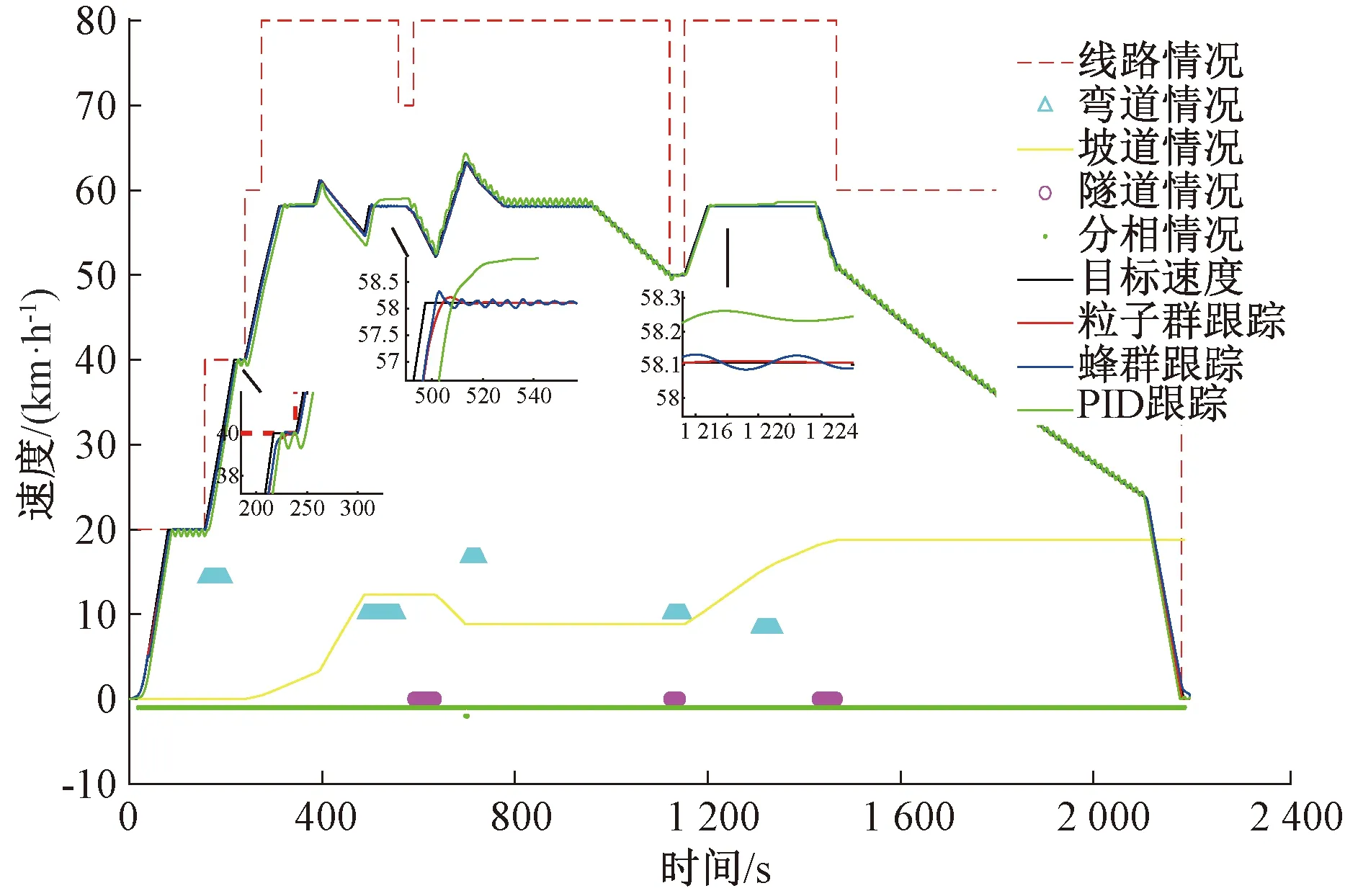
图8 三种算法的目标速度跟踪曲线比较

由图8可知，在200～250 s加速阶段，基于改进PSO算法速度跟踪曲线无超调且无振荡，克服了PID算法出现的小幅震荡的缺点，能够达到节能的要求；在500～600、1 200～1 500 s的匀速段，基于改进PSO算法的速度跟踪曲线几乎与目标曲线重合，实现了对目标速度的精确跟踪，克服了PID的大超调与蜂群算法的小波动、微超调的缺点，这就极大地降低了实际的控制难度，避免了实际中的执行机构的振荡的缺点，同时达到节能的目的。

三种算法跟踪误差见图9,由图9可知，基于ADRC的速度跟踪比PID具有精确的效果，虽然与目标速度曲线略有偏差，但可以快速修正，这表明ADRC控制器的控制精度较高和抗干扰能力较强。

图9 三种算法跟踪误差

5 结论

本文针对货运列车速度跟踪控制，设计了一种基于改进粒子群算法的自抗扰控制器。设计二阶非线性自抗扰控制器，提高了系统的抗干扰性，同时利用改进粒子群算法优化自抗扰控制器参数，采用自适应权重法改进惯性权重，避免算法陷入局部最优，提高了系统的收敛速度。在相同仿真条件下，与经典PID控制算法和基于人工蜂群算法进行对比分析，仿真结果表明，该算法具有抗干扰性能较强，速度跟踪精度较高，响应速度较快的优点，适用于列车速度跟踪控制。