全并联AT牵引网行波传播特性研究及单端故障测距算法

傅钦翠，陈剑云,钟汉华，周 欢，华 敏

(华东交通大学 省部共建轨道交通基础设施性能监测与保障国家重点实验室，江西 南昌 330013)

全并联 AT(Auto Transformer)牵引供电系统广泛应用于高速铁路中，牵引网故障的精确定位对保障铁路安全运行具有重要的意义。现有的故障测距装置大多基于阻抗测距原理[1-2]，故障信息来源于低频稳态量，受工况影响波动较大，其定位准确性与可靠性很难有提高的空间，因此，探索新的测距方法是缓解传统测距方法可靠性差的重要途径。行波测距法基于高频行波暂态量，且不受过渡阻抗等因素的影响，具有更好的研究和应用前景。

单端行波故障测距方法是当前现场应用较多的一种行波测距方法，在提高单端测距方法可靠性方面，学者们从不同线路结构下行波传播与折反射传播规律出发，分析故障行波反映和表征故障位置的机理，提出相应的测距方法[3]。文献[4]分析了到达检测母线的各个行波波头极性组合反映线路的不同故障区段的机理，以行波波头极性组合为判据，推导出对应不同区段的故障测距算法。文献[5]提出考虑电流行波极性和电压行波极性的综合行波极性判别法。

对于具有特殊结构的AT牵引网而言，要实施有效可靠的单端故障行波测距存在如下问题。首先，线路中并联了低漏抗的自耦变压器，而有关自耦变压器对行波造成影响的相关研究不多。文献[6]认为，故障行波频率较高，在理想情况下可将自耦变压器绕组看作开路，即认为自耦变压器对行波不造成影响。然而，由于电气化铁路对AT专用自耦变压器有低阻抗的要求[7]，远低于常规电力变压器标准阻抗，简单地将自耦变压器绕组看作开路并不合适，自耦变压器对行波传播造成的影响还有待分析，对自耦变压器进行合理地电磁暂态建模十分必要。

其次，AT 牵引网上下行线路并线架设，且每隔一段进行并联连接，其行波传播的特点，供电臂出线端检测到的电压、电流行波所含故障信息与发生故障的区段、位置的映射关系有待深入分析。文献[8-9]直接采用基于单回线的行波测距方法，该方法没有利用同杆双回线自身的故障特征；文献[10]针对同杆双回线路研究其行波传播特点；文献[11]研究了双回线路多模分量传播规律。因此，AT牵引网行波传播规律及特点是一个需要重点研究的课题，可为AT牵引网故障行波测距算法的建立和产品研制奠定理论基础。

本文首先建立AT自耦变压器的电磁暂态模型，然后结合线路相模变换解耦，将行波分解为同向模量和反向模量，解析计算同向模量在并联连接处的波过程，得到同向模量的时域表达式，并进行仿真验证分析。在行波各模量传播特点的分析基础上，利用反向模量只在故障发生区段内折反射及同向模量通过AT后衰减加剧的现象判定故障发生区段，对不同区段提出行之有效的行波故障测距算法。

1 全并联AT牵引供电系统

1.1 供电系统结构

相对于其他供电方式而言，AT供电方式具有更好的防干扰效果和更大的供电潜力，特别适合于高速、重载铁路[12]。全并联 AT 牵引供电系统见图1，牵引变电所(Traction Substation，TS)主变压器二次侧±27.5 kV端子分别接于接触网和正馈线，二次侧线圈中点接于钢轨。每隔10～15 km，将自耦变压器并入接触网和正馈线之间，AT自耦变压器中点与钢轨相连接，在 AT 处通过横连线将上下行线路进行并联连接，实现上下行接触网的并联运行。正常运行情况下，牵引变电所向上下行接触网并行送电，每个供电臂长30～50 km，中间设置1～2个AT，将供电臂分为2～3段。

T、R、F分别为接触线、钢轨、正馈线；Rr为钢轨电阻。图1 全并联 AT 牵引供电系统示意图

接触网的悬挂断面见图2。由上下行接触线CW、承力索MW、正馈线PF、保护线PW、钢轨R、综合接地线CGW构成，各导线参数见表1(其中钢轨的导线等效半径采用文献[13-14]基于有限元的分析结果)。本文采用多导体传输线建模方法，将接触线和承力索建模为一根二分裂导线，左右两根钢轨也建模为一根二分裂导线，合并分裂导线并消去地线后，上下行线路等效为六相等值相导线。

图2 接触网悬挂断面(单位：mm)

1.2 AT供电专用自耦变压器的电磁暂态建模

在AT 供电系统中，自耦变压器的使用不但可以大大降低牵引网中的电压损失，保障机车负荷的供电质量，还可以降低对通信线路的干扰，是其中的关键设备。在电气化铁路这一特殊环境下，自耦变压器漏阻抗对其防通信干扰性能及增压效果影响很大，漏阻抗越低，自耦变压器的防干扰、增压效果越好。根据TB/T 2888—2010《电气化铁路自耦变压器》[7]规定，AT电气化铁路自耦变压器的短路阻抗，折算至27.5 kV侧为0.45、0.9 Ω 或1.8 Ω，综合各方面因素，目前一般选0.45 Ω，可以很好地满足AT 供电系统的要求，与常规电力变压器相比，这是一个相对很小的阻抗。

表1 导线参数表

在行波暂态量的研究中，对于线路边界存在变压器等电感性质元件的通常做法是将线路末端边界近似视为一电感元件，含丰富高频成分的电压行波在线路末端近似于开路[3]。对于低漏抗的自耦变压器来说，近似于开路可能造成较大的误差。同时，高频下自耦变压器绕组的杂散参数将起作用。因此，对自耦变压器进行合理地电磁暂态建模至关重要。

在EMTP电磁暂态仿真软件中常用的一种变压器表示法——矩阵表示法(BCTRAN模型)[15]，适用于10 kHz以下低频和中频瞬态中的变压器建模，然而故障行波频率范围较大，当频率较高时，如行波信号的高频部分(几十kHz至几百kHz)、雷电过电压的计算，还需要考虑绕组对地以及绕组间的电容。文献[16]在计算中低压配电网雷电过电压中，分析了几种表示变压器的高频模型对计算结果的影响，并通过实验室测量进行了识别和验证，得出π电容+BCTRAN的模型更为精确，其频率响应特性与实验室测试结果基本吻合，可以精确地模拟高频下的变压器。综上所述，针对行波暂态量的研究，考虑电容特性的AT专用自耦变压器电磁暂态模型见图3，图3中P、S分别为高压、中压绕组端子，N为公共端。π电容C1、C2、C12采用EMTP推荐的典型值0.005、0.01、0.01 μF。

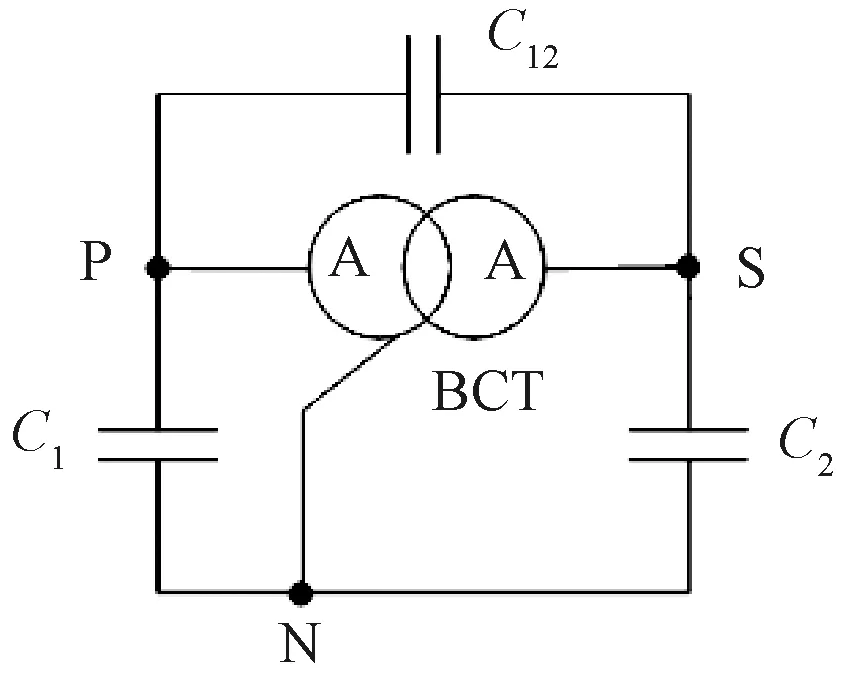
图3 考虑电容的自耦变压器电磁暂态模型

图4 单相变压器的BCTRAN模型结构

变压器电磁暂态模型BCTRAN[15]采用回路阻抗矩阵来描述，将变压器各绕组视为一组相互耦合的电感，构建变压器的等值电路模型。图4为单相变压器的BCTRAN结构和参数。绕组之间的关系通过2个多相耦合PI型电路(电容为0)来表示。第一个多相耦合PI型电路表示励磁支路，电路参数为电阻Rm，无电感。第二个PI型电路的绕组电阻矩阵为R，绕组电感矩阵为ωL或ωL-1，矩阵阶数等于绕组个数。在暂态计算中，单相变压器用如下阻抗方程表示

(1)

也可采用导纳矩阵表示

(2)

对于AT自耦变压器，将其高压-中压(P-S)、中压-低压(S-N)绕组视为两耦合线圈，如果不考虑电阻，且假定励磁电阻Rm很大，导纳矩阵L-1为

(3)

式中：iP、iS为线圈电流；uPS、uSN为线圈电压；由于两线圈匝数相同，绕组间耦合的互阻抗与自阻抗基本相近，导纳矩阵中的元素d1≈d2。

为后续行波模量波过程的解析，在此按照全并联 AT 供电的联接方式及上述的自耦变压器电磁暂态模型，利用式(3)列出并联于牵引线路中的自耦变压器的节点导纳矩阵的运算微积形式，p为运算算子，暂不考虑自耦变压器的电容特性。

(4)

式中，YAT为自耦变压器的节点导纳矩阵。

1.3 牵引网线路相模变换

全并联AT 牵引供电系统上下行接触网并行送电，结构紧凑，不仅相间存在耦合，上下行线路间也存在耦合，故障分析时需要对上下行双回线进行解耦计算。对于各相行波之间存在的电磁耦合，根据模式传输理论，进行相量和模量的变换。进行相模变换后的波动方程为

(5)

Ti=Tu-T

(6)

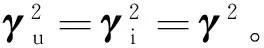
理论上，线路参数矩阵随计算频率变化而变化，但相关研究表明[17]，只要频率≥50 Hz，相模变换矩阵基本上和频率无关，因此，进行线路解耦变换时可采用不随频率改变的变换矩阵，在此计算频率取5 kHz，电流相模变换矩阵Ti为

(7)

由于牵引网上下行线路的对称性，电流相模变换矩阵具有如下形式

(8)

其中

因此，相模变换关系可以表示为

(9)

存在如下关系

(10)

式中：iⅠ=[iⅠTiⅠRiⅠF]T，iⅡ=[iⅡTiⅡRiⅡF]T，imC=[imC0imC1imC2]T，imD=[imD0imD1imD2]T。其中，电流相量的下标Ⅰ、Ⅱ表示上下行线路；电流模量表示为同向模量和反向模量的形式，用同向模量和反向模量表示可实现上下行两回线路间的解耦，下标C、D表示同向量、反向量，同向量、反向量的0模、1模、2模用下标0、1、2表示。

对于电压行波也同样存在如下关系

(11)

式中：uⅠ=[uⅠTuⅠRuⅠF]T，uⅡ=[uⅡTuⅡRuⅡF]T，umC=[umC0umC1umC2]T，umD=[umD0umD1umD2]T，并且有如下关系

(12)

式中：矩阵P=M-T/2、Q=N-T/2。

1.4 同向量和反向量行波特性分析

牵引网采用全并联 AT 供电方式，全并联 AT网将上下行线路在 AT 处通过横连线进行并联连接，上下行共用自耦变压器。根据式(10)、式(12)，可将全并联的牵引网线路分解为同向模量网络和反向模量网络。将牵引网线路发生单相接地故障下的故障分量网络分解为同向模量网络和反向模量网络，见图5，图中TS为牵引变电所出口处，由于篇幅有限，图中略去了供电臂末端的AT3。图6给出了同向模量、反向模量的行波网格图。

图5 故障分量网络分解

图6 同向、反向模量行波网格图

根据线路两端的边界条件uⅠ=uⅡ，反向模量umD=0，反向模量网络在并联连接处的电压为零，相当于对地等效阻抗为零，可视为直接接地。而同向模量在并联连接处的阻抗增加1倍，为故障分量网络的对地等效阻抗的2倍。

故障行波到达并联连接处，由于反向模量在并联连接处对地等效阻抗为零，电压行波反向模量发生负的全反射，电压行波折射系数αu=0，反射系数βu=-1，电流行波反向模量imD在并联连接处发生正的全反射，电流增加1倍，电流行波折射系数αi=2，反射系数βi=1，并联连接处的imD模分量为入射波和反射波的叠加(在节点处的电压、电流折反射系数的推导参见文献[4])。

显然，故障行波的反向模量只在发生故障的区段内折反射，不能越过AT进入另一区段。

对于同向模量而言，同向模量在并联连接处的对地等效阻抗决定了其行波的折反射。在线路首端、中间存在呈电感性质的牵引变压器、自耦变压器，同时，高频下变压器绕组的杂散电容将起作用，线路边界呈现电感或电容性质将影响行波波头的形状。下文将针对同向模量在并联连接处的波过程展开具体分析。

1.5 同向模量在并联连接处的波过程解析

同向模量在并联连接处的波过程较为复杂，在此，采用广义彼德逊法则来分析计算同向模量在并联连接处的波过程。模分量的传输线路及等值电路见图7。

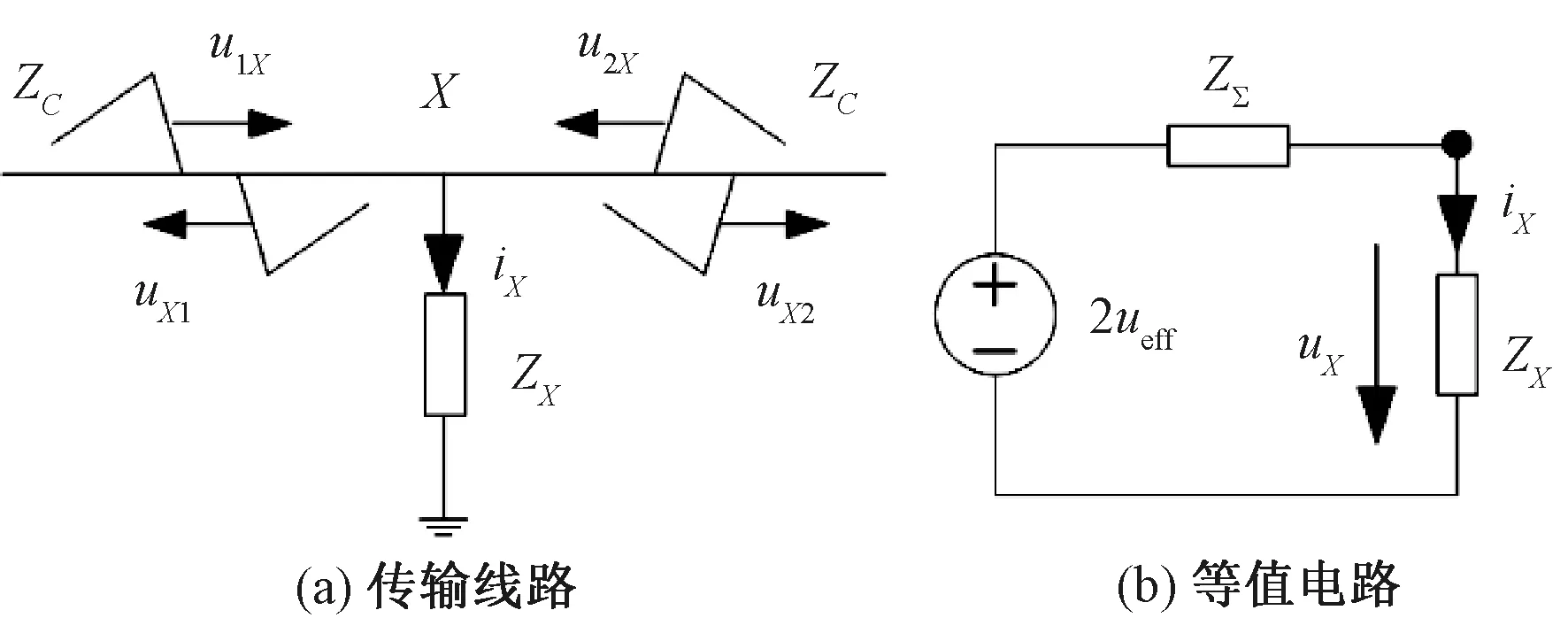
图7 模分量的传输线路及等值电路

图7(a)并联连接处为节点X，线路1、2为并联连接处两侧线路，由于并联连接处两端牵引线路参数相同，波阻抗均为ZC，ZX为模分量在节点X处的对地阻抗。假设入射到X点的电压波为u1X，u2X，从节点X反射和折射到各条线路的电压波为uX1，uX2。约定流向节点为电流的正方向，根据节点的边界条件，有

(13)

将电流波用电压波表示，有

(14)

整理式(13)、式(14),可得

2ueff=uX+ZeffiX

(15)

其中,

式中：Zeff为等值波阻抗；ueff为沿着线路入射到节点X的等值电压波。由此，得到图7(b)所示的集总参数等值电路。

应用图7(b)所示的等值电路可计算得出各模分量在并联连接处的波过程。对于行波各模分量，其ZX各不相同，各模分量在并联连接处的折反射过程也就不同。

各模分量的ZX可由相域的导纳矩阵经相模变换后求逆计算得到。按照图1全并联 AT 供电的联接方式及上述的自耦变压器节点导纳矩阵，可得并联联接处相域节点导纳矩阵Yph为

Yph=A+YAT

(16)

式中：

其中，gr为钢轨接入综合接地系统的等值导纳，gr=1/Rr(Rr通常较小，10 Ω左右)，暂不考虑自耦变压器绕组的杂散电容。

代入式(9)、式(11)，并结合式(8)，经相模变换后得模域节点导纳矩阵Ym为

Ym=Ti-1YphTi-T

(17)

考虑到d1≈d2，则

(18)

对于同向模分量，式(18)中的第1个矩阵为电导矩阵，第2个为电纳矩阵，均为满阵，说明模0、1、2分量在并联连接处有不同程度的交叉透射。如不考虑交叉透射现象，从第2个矩阵的对角线元素可看出，模0分量的电导远大于其他2个分量，其对地电阻很小，可视为零。模1分量的电纳远大于模2分量，是模2分量的几十倍。模0分量的对地阻抗约为零；模1分量的对地阻抗以感性为主，取决于自耦变压器的参数；模2分量的对地电阻较大，其电感性相对较小，可忽略。

同向模分量在并联连接处的对地阻抗ZX(i)(i=0，1，2)各不相同，则模分量在并联连接处的折反射过程也就不同。

模1分量的对地阻抗以感性为主，由图7(b)所示的等值电路，可列出X点电压的运算微积形式为

(19)

对于短路故障分量行波，初始行波波头具有明显的阶跃特征，可用直角波表示，假设故障行波由线路1入射，则u1X=E，u2X=0，2Ueff(p)=E/p，ZX(1)(p)=pLe，其中Le为等效电感，Le=k/d1，k为等值系数。

(20)

通过拉式反变换，可以得到模1分量X点电压的时域解

(21)

式中：τ为时间常数，τ=2Le/ZC，可见，模1分量X点电压以指数规律衰减，初始值为行波波头幅值，时间常数与线路波阻抗及自耦变压器的参数有关。

X点电压的时域解代入式(13)、式(14)，可得线路1、2的折反射电压、电流波时域解，此处不赘述。

若入射到X点的电压波为一指数波，即u1X如式(21)，u2X=0，则2Ueff(p)=E/(p+1/τ)，代入式(19)，拉式反变换后，得模1分量X点电压的时域解

(22)

模0分量的对地阻抗约为零，电压行波折射系数αu=0，反射系数βu=-1，电压行波发生负的全反射，X点电压模0分量约为零，电流行波折射系数αi=2，反射系数βi=1，电流行波在并联连接处发生正的全反射，电流增加一倍。

模2分量的对地电阻较大，通常大于线路的波阻抗，如视为无穷的话，电压行波折射系数αu=1，反射系数βu=0，电压行波在并联连接处只折射无反射，同样，电流行波折射系数αi=1，反射系数βi=0，只折射无反射。

对于变电所出口处的同向模量，由于牵引变压器无低漏抗的要求，短路电抗一般较大，含丰富高频成分的行波可近似于开路。与上述解析方法类似，节点的边界条件有所不同，可推导得，模0、1分量的对地阻抗约为零，电压行波折射系数αu=0，反射系数βu=-1，电压行波发生负的全反射，电流行波折射系数αi=2，反射系数βi=1，电流行波在变电所出口处发生正的全反射，电流增加一倍。模2分量的对地电阻较大，近似于开路，电压行波折射系数αu=0，反射系数βu=-1，电压行波发生正的全反射，电压行波在边界产生与入射波极性相同的反射波，所测电压模2分量为入射波和反射波的叠加。

2 仿真验证及分析

本文以图1所示的AT牵引供电系统为例，基于实际工程参数在EMTP电磁暂态仿真平台上搭建仿真模型，进行仿真分析。仿真系统中，供电臂总长45 km，中间设置2个AT，将供电臂分为3段。自耦变压器的额定容量10 MVA，空载损耗5.0 kW，负载损耗23.0 kW，空载电流0.45%，短路电压0.59%，归算至27.5 kV侧的短路电抗为0.45 Ω。

2.1 各模量传播的仿真验证

采用图1所示的仿真系统，按照如下情况进行仿真分析：假设第2段线路距离AT1 5.5 km处上行线发生TR短路故障，故障阻抗10 Ω，故障点、AT1、变电所出口处检测到的电压行波模量见图8，故障点左侧线路、AT1右侧线路、变电所出口处的检测到的电流行波模量见图9。

图8 故障点、AT1、变电所出口处的电压行波模量

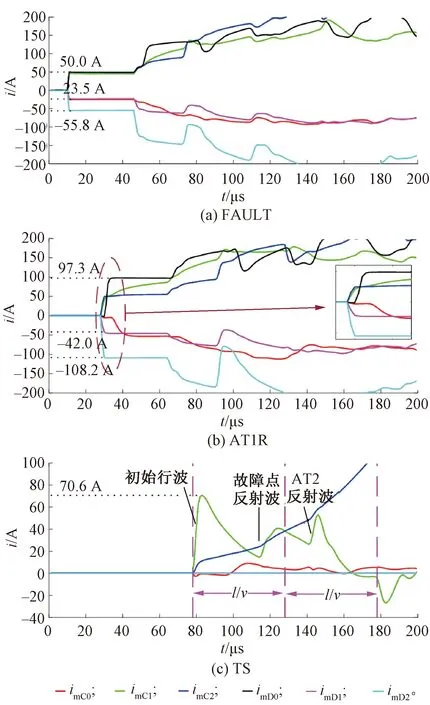
图9 故障点左侧线路、AT1右侧线路、变电所出口处的检测到的电流行波模量

由图8可知，AT1并联连接处检测到的电压行波反向模量为0，说明反射波与入射波极性相反，幅值相等。电压行波同向模0分量也约为0，同向模1分量以指数规律衰减变化，同向模2分量幅值约13.8 kV，略低于故障点电压行波幅值14.4 kV，在AT1并联连接处的反射很小，基本无反射。

变电所出口处量测点TS的电压行波反向模量仍然为0，显然故障行波的反向模量只存在于发生的故障区段，不会越过AT进入其他区段。电压行波同向模0、1分量也约为0，反射波与入射波极性相反，幅值相近；同向模2分量幅值约24 kV，约为AT1处幅值的1.7倍，如计入行波在线路上传播的损耗，该分量的反射波与入射波极性相同，幅值相近。

由图9可知，AT1右侧线路量测点AT1R的电流反向模量初始行波波头幅值大约是故障点电流行波幅值的2倍，说明电流反向模量在AT1并联连接处的反射波与入射波极性相同，幅值基本相等。电流同向模0分量初始行波波头幅值与反向模量一样，也是故障点电流行波幅值的2倍；电流同向模1分量呈现由0逐渐以指数规律增大的趋势；电流同向模2分量幅值与故障点电流幅值相近，说明其在AT1并联连接处的反射很小，约为0。

变电所出口处TS检测到的电流行波反向模量与电压行波一样，也为0。电流同向模1分量的变化曲线与AT1处的电压相同，其初始值为70.6 A，对于第1段线路，AT1处的电压相当于入射波。

图9中的量测点AT1R各模量中，同向、反向模1、2分量同时到达，反向模0分量稍稍滞后，同向模0分量最后到达，滞后约10 μs且波头上升变缓，这种现象是由行波模量通道传播参数的差异所致。通过计算所得，同向模0分量相位速度远小于模1、2分量(或称为线模分量)，衰减系数远大于线模分量，反向模0分量相位速度略小于线模分量。总的来说，线模通道具有近似相同的传播特性，衰减系数小且相位速度接近光速，因此，选择线模分量进行行波测距更准确。

2.2 自耦变压器对行波的影响分析

为验证前述AT并联连接处电压行波同向模1分量波过程解析计算方法的有效性，将式(21)的解析计算结果与EMTP仿真结果进行对比。由前述的仿真结果，故障点电压行波同向模1分量幅值16.8 kV，考虑在线路传播中的损耗，则入射的直角波E=16 kV，由选用的自耦变压器参数及线路参数计算得出，等效电感Le=1.5 mH，同向模1分量波阻抗ZC=188 Ω，时间常数τ=16 μs。图10中虚线为式(21)的解析计算结果，红色实线为仿真所得AT1电压行波同向模1分量波形，可见，解析结果与仿真所得行波初始波头波形基本吻合，说明前述波过程的解析计算方法是合适的。

改变自耦变压器的漏阻抗，分析自耦变压器的漏阻抗对行波形状的影响。图10中实线(红、绿、蓝色)对应自耦变压器的短路电抗(归算至27.5 kV侧)分别为0.45、0.9、4.5 Ω时，AT1电压同向模1分量umC1的EMTP仿真波形。由图10可知，umC1初始波到波尾的衰减与AT的短路电抗有关，AT的短路电抗越低，波尾的衰减越快，短路电抗为4.5 Ω时，初始波头基本不衰减。表2列出了不同短路电抗下umC1的初始波头的衰减时间常数，时间常数与AT的短路电抗基本成正比。显然，在使用低漏抗的自耦变压器的牵引供电系统中，不能简单地将自耦变压器绕组看作开路，认为自耦变压器对行波不造成影响。

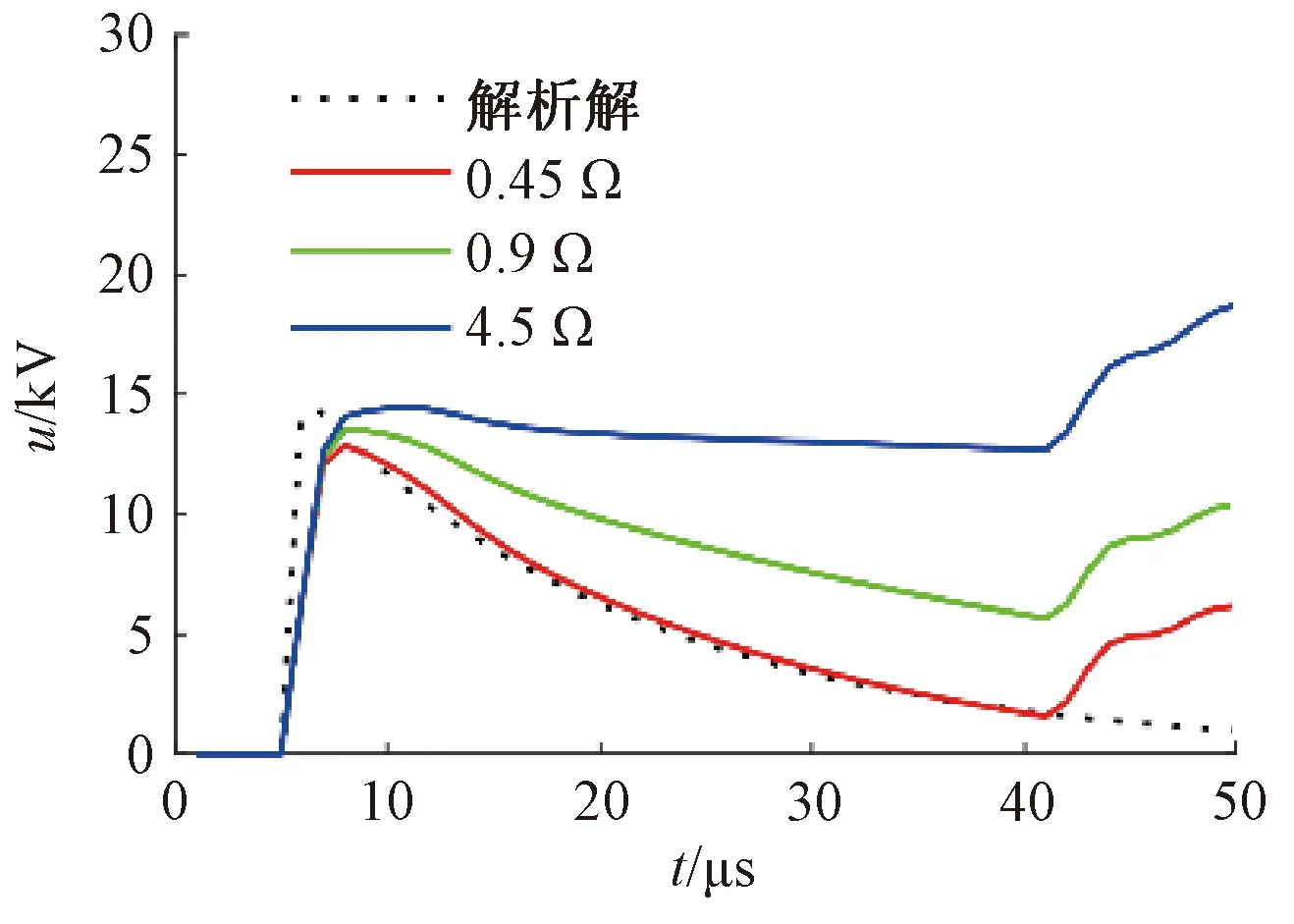
图10 AT1处umC1的解析解及不同短路电抗下的仿真波形

表2 不同短路电抗下umC1的衰减时间常数

高频下自耦变压器绕组的杂散参数将起作用，需要考虑自耦变压器绕组对地以及绕组间的电容对行波的影响。绕组电容对行波波头的影响见图11，由图11可见，绕组对地电容对电流行波波头影响较大，电流行波波头出现尖峰，尖峰的存在对于测距装置识别波头存在一定程度的干扰，绕组对地电容使电压行波波头的上升变缓，斜率降低。因此，选用电压行波进行测距效果较好。

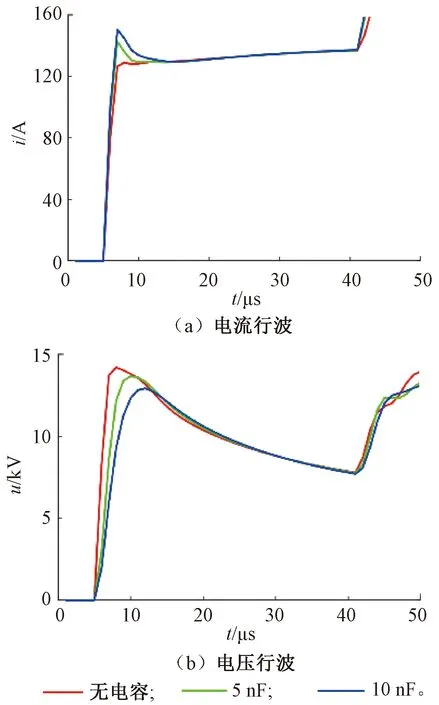
图11 绕组电容对行波波头的影响

2.3 对比故障发生在不同区段时的行波

为了分析在变电所出口处所测得的电压、电流行波所含故障信息与发生故障的区段的映射关系，在第1、2、3区段线路距离段首端 5.5 km处，上行线发生TR短路故障的3种情况分别进行仿真。

故障发生在第1、2、3段时，在变电所出口处量测的电流行波同向模1分量imC1初始波到浪涌的对比见图12。由图12可知，当故障发生在第1段时，变电所出口处的imC1初始波到浪涌为直角波；发生在第2段时，imC1以指数规律衰减，其变化规律与入射波为直角波时AT1并联连接处的电压相同，见式(21)；发生在第3段时，imC1的波尾衰减更快，其变化规律与入射波为指数波时AT1并联连接处的电压相同，见式(22)，在经过2个低漏抗的自耦变压器后到达变电所出口处的过程中，故障行波到达AT2处时由直角波变为指数波，传播至AT1处时由指数波变为如式(22)的波形，初始波到浪涌呈现波尾快速衰减的形状。

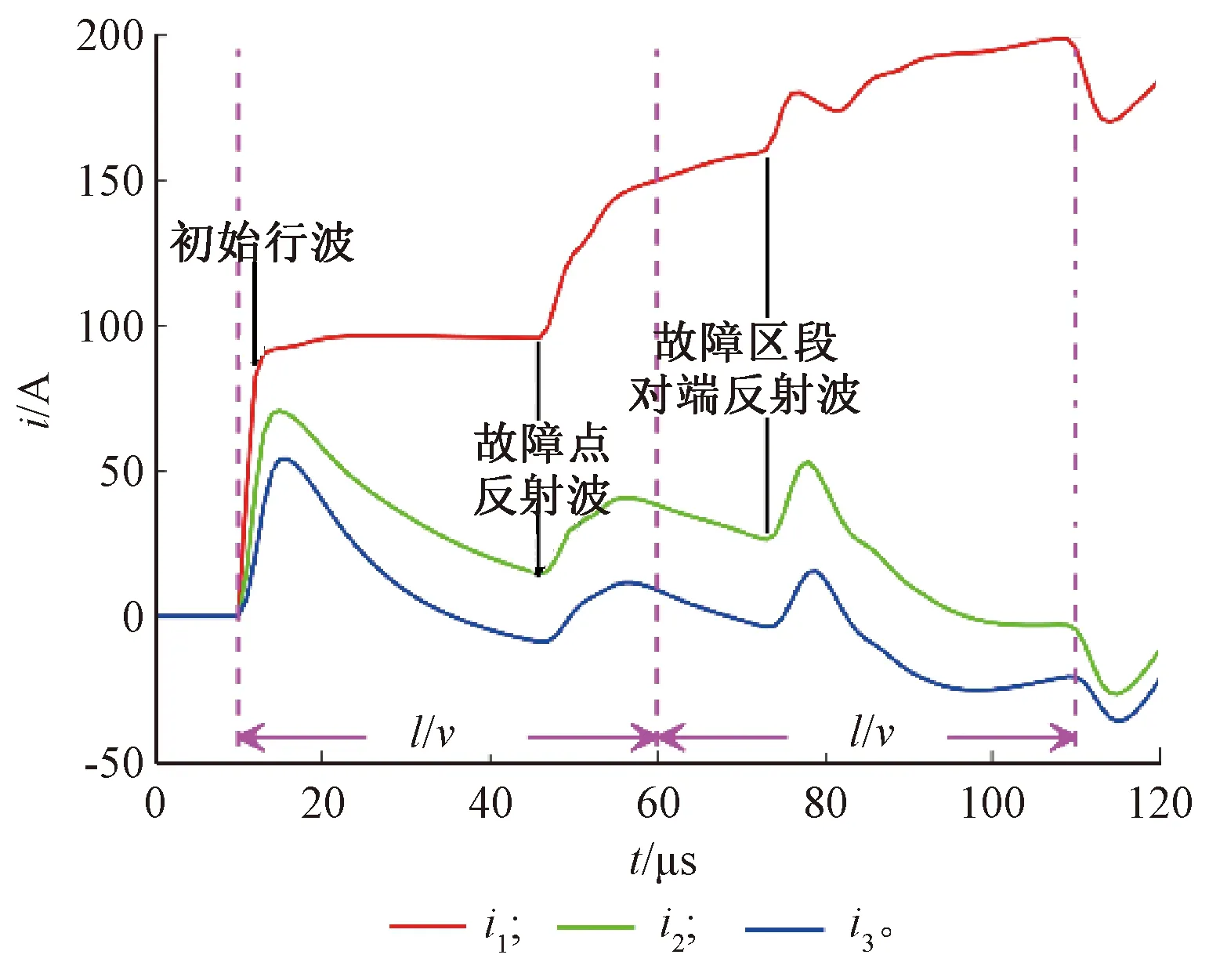
图12 不同故障区段下的变电所出口处imC1

故障发生在第1、2、3段时，变电所出口处观测的电压行波同向模2分量umC2对比见图13。由图13可知，在不同区段发生故障时，在变电所出口处观测的电压波形相差不大，显然，利用电压行波无法判别故障发生的区段。

FR、TF短路故障时的情况与TR故障的类似，此处不赘述。

图13 不同故障区段下的变电所出口处电压umC2

3 单端故障行波测距算法

基于上述AT牵引网行波模量传播特点的分析，结合牵引网的线路特点，确定合理有效的单端故障行波测距算法。

3.1 判断故障发生区段

上下行线路全并联连接下，由于故障行波的反向模量只在故障发生区段内折反射，当故障发生在第2、3段时，在变电所出口处所测得的电流行波反向模量imD为零，而故障发生在第1段时，imD不为零。据此，可利用电流行波反向模量来判断故障发生的区段是否为第1段，在此基于前述的模分量传播特性分析，选择衰减小的线模分量，反向模1或2分量imD1、imD2。

对于故障发生在第2、3段的情况，由2.3节的对比分析可知，在第3段产生的故障行波通过2个低漏抗的自耦变压器后，在变电所出口处检测到的同向模1分量imC1初始波到波尾衰减加速，可利用波尾形状特征并结合式(21)、式(22)来判断故障是发生在第2段还是第3段。

3.2 确定故障点位置

单端行波测距方法通过初始波头及其后续反射波的到达测点时差来确定故障距测点的位置，具有经济性强且不依赖数据时钟同步的优势。波头到达时刻的准确标定及辨识是单端测距方法得以成功实施的关键，前提是可靠地检测、辨识出测距所需的有效波头。

在AT牵引网中应用单端行波测距方法存在如下问题，受AT自耦变压器、杂散电容、故障阻抗等多方面因素的影响，电流行波波头出现短时尖峰，后续反射波上升斜率低等现象，影响行波波头到达时刻的准确标定。仿真分析表明，故障发生在第2、3段时，在变电所出口处观测到的电流行波反射波波头上升平缓，电压行波受自耦变压器、杂散电容等的影响较小，发射波的幅值和陡度都较强，较易捕捉、标定与识别。因此，当观测点设置在变电所出口处确定第2、3区段的故障点位置，不宜采用电流行波来标定波到时刻，应采用电压行波。

对于第2、3区段的故障点位置的确定，变电所出口处观测点只有行波同向模量，由图6分析得到如下结论，在行波同向模量初始波到后的2li/v(i=1，2，3)时间窗内有第1次故障点反射波和本故障区段对端AT反射波，两者分属于前后2个相继的li/v时间窗内，本段线路半线长内故障时故障点反射波先到达，而半线长外故障时对端反射波先于故障点反射波到达。由于故障点过渡电阻只使故障点反射波幅值减小，并不改变波尾形状，而故障行波到达对端AT后在自耦变压器作用下其反射波波尾衰减将加剧(如图12所示的imC1)，利用此特点，可判断反射波是由故障点反射而来，还是由对端AT反射而来，继而判断故障点是位于半线长内还是半线长外。最后，后续反射波以初始行波波到t0为起点的波到时刻tA、tB总是关于li/v时刻点对称，可利用tA+tB=2li/v核验测距结果。

对于第1区段的故障点位置的确定，鉴于电流行波反射波受AT自耦变压器的影响较小，可利用在变电所出口处检测到的电流行波反向模量标定波到时刻tA、tB，并根据电流反向模量imD2的极性变化判断半线长内外。

3.3 单端故障测距算法流程

针对图1的AT牵引网，列出单端行波故障测距算法流程，见图14。

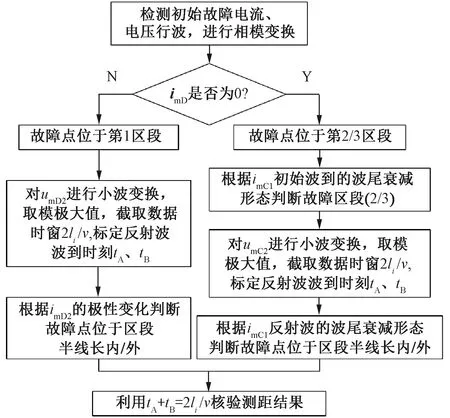
图14 故障测距算法流程图

3.4 故障测距仿真

分别对图1所示AT牵引网在不同区段不同位置发生TR短路故障进行仿真，仿真步长1 μs，提取牵引变电所出口处的故障电流、电压行波，利用上述测距算法计算故障距离，行波传播速度取线模分量的波速v=2.956 9×105km/s，仿真结果见表3。测距误差均小于200 m。可见，利用所提出的单端测距算法可获得较高的测距精度和稳定性。

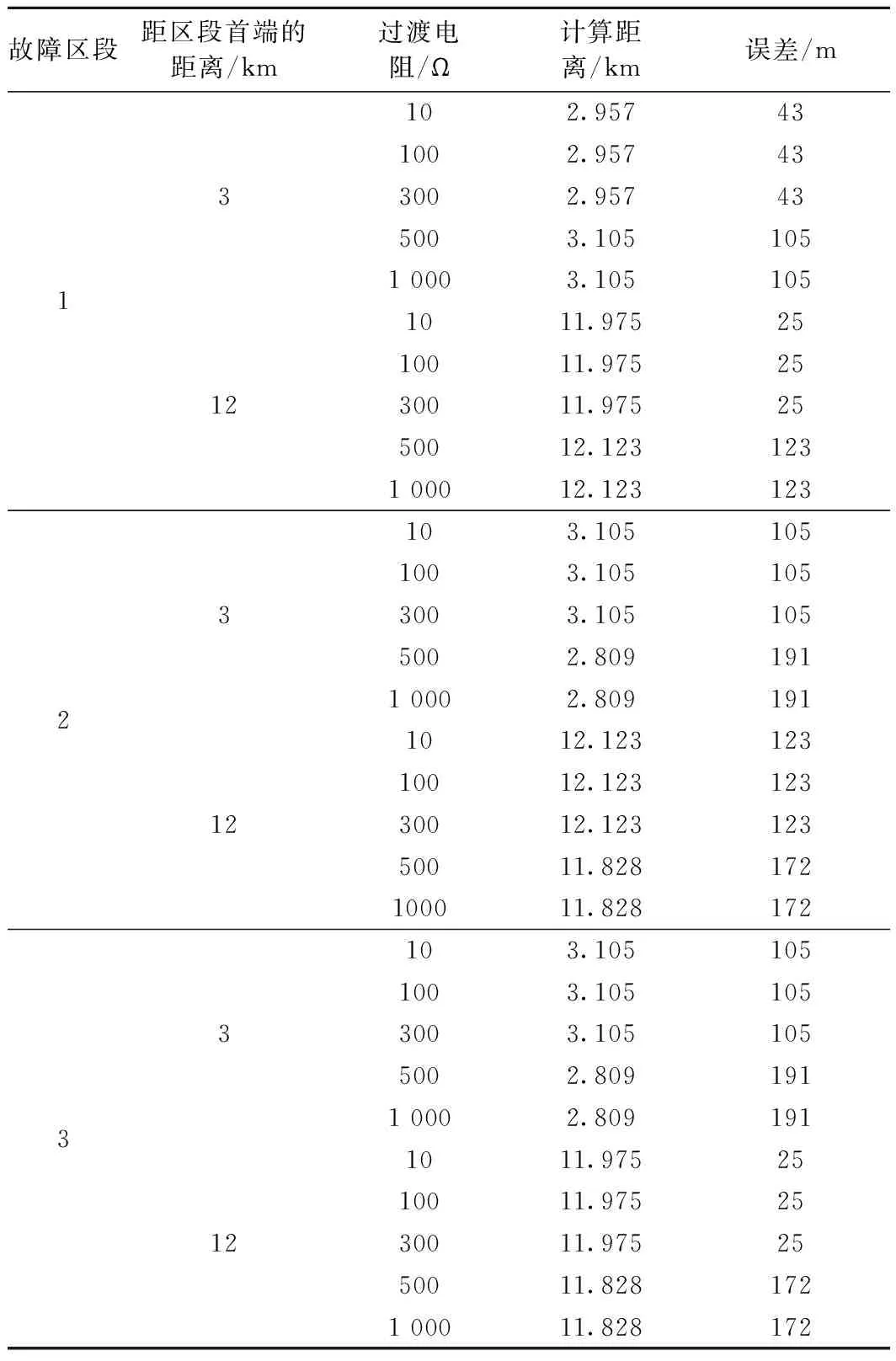
表3 故障测距仿真结果

4 结论

(1)建立了AT自耦变压器的电磁暂态模型，基于该电磁暂态模型，结合相模变换，推导出行波同向模量在AT并联连接处的波过程时域表达式，并仿真验证了解析解的正确性，揭示了波到的波尾衰减形状与自耦变压器的漏阻抗的关系。

(2)对AT牵引网上下行线路进行解耦，将行波分解为同向模量和反向模量，分析了行波各模量的传播特点，得到反向模量只在故障发生区段内折反射的结论。

(3)在上述分析的基础上，提出利用反向模量只存在于故障区段内及同向模量通过AT后衰减加剧的现象来判定故障区段的单端行波故障测距新算法。