力的合成与分解演示实验仪

徐爱婷，唐义甲

（1.丰城二中 物理教研组，江西 丰城 331100；2.阜阳师范大学 物理与电子工程学院，安徽 阜阳 236037）

0 引言

物理学是一门以实验为基础的学科，而力学是物理学最重要和最基础的内容之一[1,2]。在大学物理教材中力被定义为物体间的相互作用[3]。演示实验是力学教学的重要环节之一，一般演示实验是由授课教师利用演示实验仪演示实验过程，展示实验现象，引导学生观察、思考、分析实验现象，得出结论，也可以由学生自己进行演示。演示实验是一种直观、简单的教学手段，有利于激发学生的学习兴趣，培养学生的探究能力，养成科学严谨的思维方式等。受时间和环境的限制，演示实验仪应简单、方便操作、重复性好[4,5]。

力学是物理学的重要分支之一，力学主要研究物体的机械运动[3]。为了探索物体的机械运动规律，必须对涉及到的物体进行受力分析，利用牛顿第二定律建立物体运动的动力学方程，进而求解动力学方程，获得物体运动的规律。而力作为矢量，运算法则比较复杂，力的合成遵循平行四边形法则。为了简化矢量的运算，人们通常建立直角坐标系，将矢量投影到坐标轴上进而将矢量运算转化为标量运算[6,7]。

力是物理学中最重要的矢量之一，教学中力的合成与分解既是难点又是重点[8,9]。市面上力的合成与分解演示仪相对较少，而且结构复杂，功能简单。为了帮助学生理解力的合成与分解规律，掌握力的运算法则，设计并制作了一种力的合成与分解的演示仪。通过课堂演示实验，直观地揭示了力的矢量性及力的合成与分解所遵循的规律，并在丰城地区的中学进行了推广，获得了良好的教学效果。

1 演示仪器的设计与制作

基于滑轮组对力的方向的调制性和力的等值传递性以及钩码重力与质量成正比的性质，辅以透明360°圆形测角仪和平行四边形刻度尺、PVC 演示板等设计了力的合成与分解演示试验仪。

制作过程简介：选一块厚度约8mm，长、宽分别为60 cm 和50 cm 的白色PVC 板，PVC 板上端设有悬挂点，可将演示板悬挂于黑板上，并配备可调高度支架，演示工作人员亦可将演示仪平放在讲台或实验台上。PVC 演示板表面光滑，可平铺坐标纸或白纸以便作图。悬挂点下方设有支撑架，可悬挂测力计。测力计下方设有360°圆形测角仪，测角仪前方为可调节翼形螺钉滑动刻度尺，滑动刻度尺可以调成平行四边形。带夹子可升降、可旋转调节的定滑轮共3 个，其中一个定滑轮位于演示板下方，另外两个定滑轮分布在演示板的两侧，并可固定在指定位置，定滑轮通过均匀的轻质弹性细线与钩码相连。这些材料在日常生活中随处可见，部分材料为废弃物的再利用。调节定滑轮位置即可改变分力的夹角。分力的量值可由增减钩码进行调控，如图1 所示。由于细线为弹性细线，在弹性限度内满足胡可定律，即细线所受的应力与相对伸长成正比，故分力量值与弹性细线的拉伸长度正相关，可在平行四边形刻度尺上直接读出拉伸长度进而确定分力的量值，因而能够直观显示分力的大小。调节平行四边形刻度尺的两边与分力平行，所以平行四边形刻度尺上侧顶角即为两分力的夹角，角度的大小可由360°圆形量角器测出。理论上，已知平行四边形的顶角与两个相邻的平行四边形的边长，便可通过余弦定理计算出刻度尺四条边所形成的平行四边形对角线的长度，从而可以验证遵循平行四边形法则的对角线长度所代表的力的量值，由对角线长度对应力的量值与测力计测出的力进行对比，同时判断平行四边形的对角线与测力计下方拉出的细线所在直线方向是否一致，来验证力的合成与分解是否遵循平行四边形法则。

图1 演示仪示意图Fig.1 Schematic diagram of demonstration instrument

2 演示实验的效果分析

2.1 二力平衡演示

图2 二力平衡演示示意图Fig.2 Schematic diagram for demonstration of equilibrium of two forces

调节定滑轮顶端位置与测力计自然伸长状态齐平，当两定滑轮下方悬挂质量相同的砝码时，两钩码处于平衡状态。由此说明，滑轮之间绳子任意一点所受的力为平衡力，测力计亦测得合力为零。钩码质量10g～200g 不等，测力计在定滑轮上方水平细绳各点均可测出合力为零。

2.2 力的合成与分解演示

如图3 所示，固定左侧钩码质量，改变二分力夹角θ与左侧钩码质量，调节平行四边形刻度尺上两边与分力平行，角度θ由圆形量角器测量。测力计测出力F对右侧钩码质量和角度θ的依赖关系，即可确定合力与分力量值之间的关系，合力方向与分力方向由圆形量角器进行测量。调节平行四边形刻度尺上侧两边与两分力F1、F2平行。

图3 力的合成与分解演示示意图Fig.3 Schematic diagram for demonstration of resultant and decomposition of forces

演示实验结果见表1，改变右侧钩码质量可调节力F2的量值，角度θ可通过移动右侧滑轮位置控制。固定左侧钩码质量为100g 时，测出力F对右侧钩码质量和角度的依赖关系，右侧分力理论上应为右侧钩码的质量与重力加速的乘积，可根据胡可定律通过平行四边形刻度尺进行测量，经验证力的合成与分解基本符合平行四边形法则或三角形法则，但略有偏差，因为理想情况忽略了滑轮摩擦力与细绳的质量。

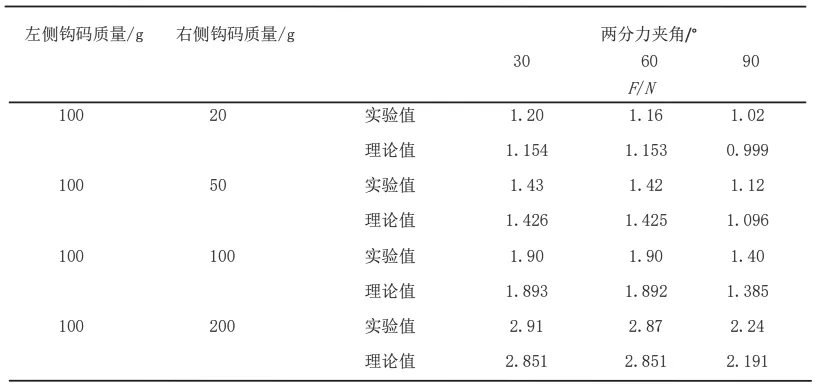
表1 力的合成与分解演示实验结果Table 1 Demonstration experiment results for resultant and decomposition of forces

将演示实验结果与理论计算结果进行对比可以发现，力的合成与分解遵循矢量法则，实验结果与理论计算结果间的误差较小。为了将误差量化，明确合力对分力夹角与钩码质量的依赖关系，做出了合力的实验值与理论值对分力夹角与分力量值（应为m2g)的依赖关系，如图4 所示。

图4 合力对分力与分力间夹角的依赖关系Fig.4 The relationship between resultant force and decomposed force

由图4 可以发现，当分力夹角固定时，分力越大，合力越大；而同一分力，分力间的夹角越大，合力越小。实验结果与理论结果符合得较好，无明显偏差，表明演示仪的实验精度较高。

误差随合力、分力与夹角的变化关系如图5 所示，由图5 可以发现固定左侧钩码质量、右侧钩码质量在20g～200g 变化时，相对误差均较小。钩码质量较小时，误差相对略大，约3.5%。这是因为当分力较小时，细线质量与滑轮摩擦力与分力相比不再是高阶无穷小量。为了提高实验精度，可对理论模型进行修正，将细线质量与滑轮摩擦力的影响视为一阶小量。

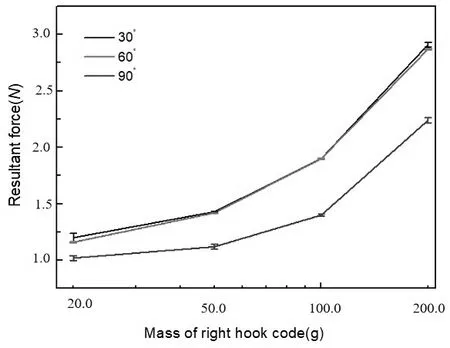
图5 误差与合力、分力及分力间夹角的关系Fig.5 The dependence of relative error on resultant force,decomposed force and the angle between decomposed forces

3 结束语

本文介绍了所设计制作的演示仪的设计思想与演示结果，并在教学过程中进行了演示，在丰城地区的中学进行了推广，获得了师生的一致好评。当钩码质量较大时，滑轮摩擦和细绳质量的影响较小，演示效果较好。当钩码质量较小时，滑轮摩擦和细绳质量的影响应视为一阶小量，忽略滑轮摩擦和细绳质量时相对误差约3.5%，与一般的力学实验结果误差无显著偏差。演示仪便携，可悬挂于黑板亦可摆放在实验台上，方便学生观察。在教学实践活动中，借助力的合成与分解演示实验仪，可直观说明力的运算法则，有利于调动学生学习的积极性，启发学生思考，帮助学生形成创新思维。