SHFuzz:A Hybrid Fuzzing Method Assisted by Static Analysis for Binary Programs

Wenjie Wang,Donghai Tian,2,*,Rui Ma,Hang Wei,Qianjin Ying,Xiaoqi Jia,Lei Zuo

1 School of Computer Science and Technology,Beijing Institute of Technology,Beijing 100081,China

2 Key Laboratory of Network Assessment Technology,Institute of Information Engineering,Chinese Academy of Sciences,Beijing 100049,China

3 School of Cyber Security,University of Chinese Academy of Sciences,Beijing 100049,China

4 NSFOCUS Inc.,Beijing 100089,China

Abstract:Fuzzing is an effective technique to find security bugs in programs by quickly exploring the input space of programs.To further discover vulnerabilities hidden in deep execution paths,the hybrid fuzzing combines fuzzing and concolic execution for going through complex branch conditions.In general,we observe that the execution path which comes across more and complex basic blocks may have a higher chance of containing a security bug.Based on this observation,we propose a hybrid fuzzing method assisted by static analysis for binary programs.The basic idea of our method is to prioritize seed inputs according to the complexity of their associated execution paths.For this purpose,we utilize static analysis to evaluate the complexity of each basic block and employ the hardware trace mechanism to dynamically extract the execution path for calculating the seed inputs’ weights.The key advantage of our method is that our system can test binary programs efficiently by using the hardware trace and hybrid fuzzing.To evaluate the effectiveness of our method,we design and implement a prototype system,namely SHFuzz.The evaluation results show SHFuzz discovers more unique crashes on several real-world applications and the LAVA-M dataset when compared to the previous solutions.

Keywords:hybrid fuzzing; static analysis; concolic execution;binary programs

I.INTRODUCTION

With the popularization of the software techniques,more and more attention has been paid to the research of software security[1–4].Among them,fuzzing could effectively find security bugs(or vulnerabilities)in programs by generating a large number of test cases.Thanks to the high speed and simplicity,fuzzing can quickly explore the input space of programs.In recent years,fuzzing has been widely adopted in both academia[5–7]and industry[8–10]for software testing.However,this technique still suffers from discovering vulnerabilities hidden in the deep execution paths of a program.The main reason is that fuzzing blindly mutates the input values,which is not good at passing complex branch conditions[11].To address this issue,many solutions have been proposed,and they often utilize some program analysis techniques to assist fuzzing,such as static analysis[12,13],taint tracking[14,15],and symbolic execution[11,16,17].Hybrid fuzzing is one of these techniques.It combines fuzzing and concolic execution.Since the concolic execution is good at solving complex branch conditions,the hybrid fuzzing has a potentially good effect on vulnerability discovery.

In our observation,the seed inputs that access more basic blocks may have a higher possibility to trigger bugs.The potential reason is that more basic blocks may have more complex program logic,and it would be prone to error during the software development.Moreover,different basic blocks may have different complexity,and it would be better to pay more attention to the complex basic blocks that have more operations,complicated structure,and vulnerable function calls.In general,the basic block is a straightline code sequence without complicated structure,and it contains at most one function call.To evaluate the structure complexity of basic blocks,it would be better to first measure the complexity of the related functions containing more structure information,and then evaluate the complexity of basic blocks.By doing so,the measurement can not only reflect the structure complexity,but also avoid some simple basic blocks being ignored.

Based on the above observation,the seeds that comes across more and complex basic blocks could be selected frist and allocated more mutation energy.For example,Listing 1 is sample code snippets from theparseline()function of thenasmprogram.It contains a buffer over-read bug caused by uncontrolled access tonasm-regflags(i.e.,CVE-2018-8883).This bug is triggered by a long sequence of basic blocks,which has complicated logic and contains some complex basic blocks.We can observe that it would be better to test the deep and complex execution paths more times than the other paths.However,many hybrid fuzzers successively select seeds in the order of their generation.This strategy may not be effective for testing as it may take a long time to select the seed inputs that can trigger program bugs.Moreover,many fuzzers utilize a uniform power scheduling policy when calculating the mutation score.However,a different execution path may have a different chance of containing a bug.Therefore,the uniform power scheduling strategy may not help to find a bug in a targeted manner.

To address the above problems,we propose a hybrid fuzzing method assisted by static analysis.The basic idea of our method is to prioritize the seed inputs according to the complexity of their associated execution paths,which is based on an observation that the execution path that comes across more and complex basic blocks may have a higher chance of containing a bug.Accordingly,our fuzzer will allocate more mutation energy for the associated seed inputs.To this end,we take advantage of static analysis toextract each basic block’s complexity weights at first.Then,we utilize Intel PT(Intel Processor Trace)[18]mechanism to collect the basic block sequence of each execution path efficiently.Thanks to Intel PT,our system can test binary programs efficiently without using instrumentation(or emulation).Finally,we calculate the complexity weights of each execution path by analyzing weights of all basic blocks inside this path.Since fuzzing and concolic execution are good at exploring different execution paths,we use two different weights,namely the fuzzing weight(denoted by’FW’for short)and the concolic execution weight(denoted by ’CEW’ for short).The FW mainly focuses on the complexity of basic blocks while the CEW focuses on the instructions related to path constraints.When fuzzing a program,we first calculate the FW and the CEW of each seed input dynamically with the help of Intel PT.Then,we perform the seed prioritization and power scheduling based on the weights of each seed.In general,a seed input with higher weights will be selected first and allocated more mutation energy.

Listing 1:Code snippets from nasm,parse_line()function.

Additionally,we mark a seed as a stuck state when the fuzzer generates fewer useful inputs based on this seed.This state indicates the seed may get stuck due to some complex branch conditions that prevent it from finding new paths.These stuck seeds will be processed by the concolic execution preferentially.On the other hand,to avoid the concolic execution generating seed inputs that cover the duplicated execution paths reached by the fuzzer,we import the fuzzer’s code coverage bitmap to the concolic execution.When the concolic execution tries to generate an input,it checks the shared bitmap at first.In this way,our method can improve the synergy between fuzzing and concolic execution.

To evaluate the effectiveness of our method,we design and implement a prototype system,namely SHFuzz.We conduct experiments on the real-world programs and the LAVA-M dataset[19].The experiment results show SHFuzz can discover more unique crashes than previous works like PTfuzz[20].More importantly,one of the bugs which are found by our system has been assigned a CVE ID(i.e.,CVE-2019-20352).

Overall,our contributions can be summarized as follows:

•We propose a hybrid fuzzing method assisted by static analysis.The basic idea of our method is to combine hybrid fuzzing and static analysis to prioritize seed inputs with higher complexity and vulnerability risk.

•We employ the fuzzing weight(FW)and the concolic execution weight(CEW),respectively.A seed input with a higher FW will be selected first and allocated more mutation energy by the fuzzer.A seed input with a higher CEW will be preferentially processed by the concolic execution.

•We record the stuck seed inputs and offer them to the concolic execution first.Moreover,we import the fuzzer’s code coverage bitmap to the concolic execution to avoid generating seed inputs that cover the duplicated execution paths.

•We design and implement our hybrid fuzzing system,namely SHFuzz.The evaluation results show SHFuzz can discover more unique crashes when compared to the previous solutions.

The rest of this paper is organized as follows.Section II analyzes the background and related work of this paper.Section III and Section IV describe the general architecture and the design of SHFuzz,respectively.In Section V,we describe the implementation of SHFuzz and then evaluate its effectiveness by conducting various experiments on real-world programs and the LAVA-M dataset.Section VI discusses SHFuzz’s limitations and possible solutions.Section VII concludes this paper.

II.BACKGROUND AND RELATED WORK

In this section,we introduce the background and related work of the coverage-based fuzzing and the symbolic execution.

2.1 Coverage-based Fuzzing

Coverage-based fuzzing solutions try to traverse as many programs’ execution paths as possible[21].It becomes popular especially since AFL[22]made good progress in vulnerability discovery.Thus,we take AFL as an example to show the workflow of coverage-based fuzzing.Generally,AFL employs the evolutionary algorithm to mutate seed inputs and then generate new useful inputs.Figure 1 shows the basic workflow of AFL.In the beginning,AFL receives initial seed inputs and maintains a seed queue.Then,it selects a seed input from the seed queue and mutates it to generate new inputs.To determine whether a new input is useful,it just use this input to execute the target program and then collects run-time coverage information.If the input reveals new branches,AFL will add it to the seed queue.Otherwise,this input will be discarded.AFL continues the above operations until the fuzzing is completed.Based on the above workflow,there are two critical steps in AFL:how to select a seed input from the seed queue(seed selection)and how to mutate it to generate new inputs(seed mutation)?

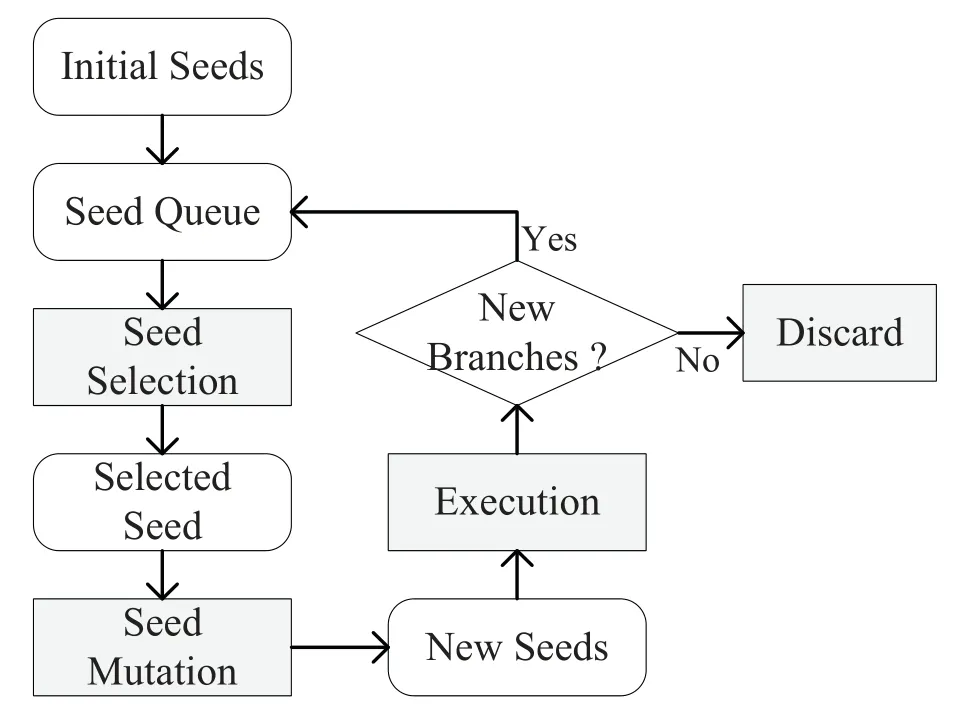
Figure 1.The basic workflow of AFL.

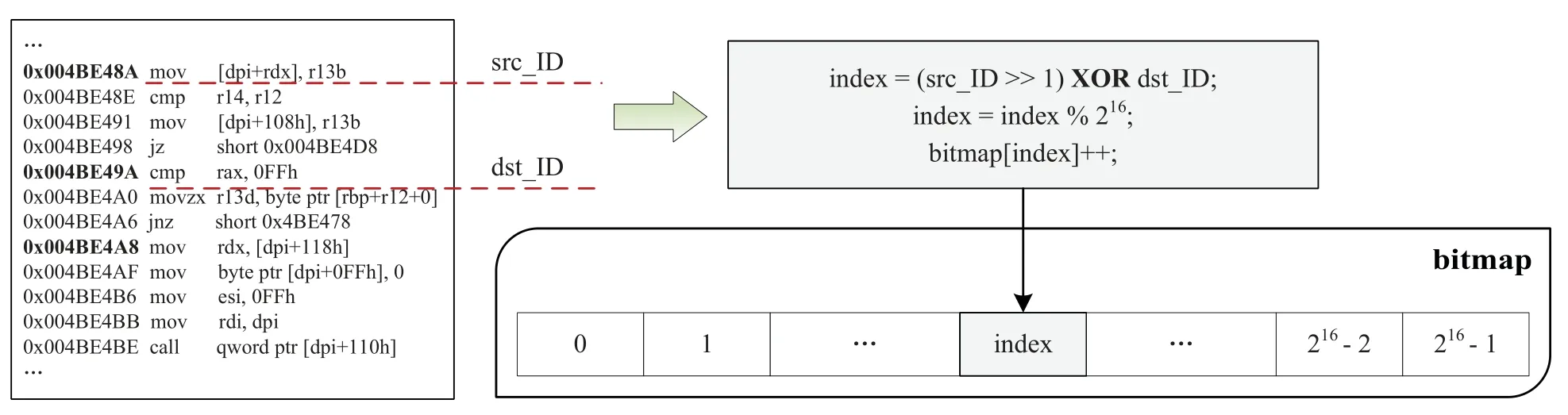
Figure 2.Bitmap in AFL.

Seed SelectionGiven the same applications,a good seed selection strategy should be in favor of finding more crashes or paths[21].In general,AFL simply prioritizes seeds that likely reveal new paths.To improve the efficiency of AFL,AFLFast[23]utilizes Markov Chain to prioritize seeds that being fuzzed fewer times.AFLGo[24]defines some dangerous code locations and selects seeds that likely reach these locations.NeuFuzz[25]utilizes the deep neural network to classify vulnerable paths and then prioritizes seed inputs that cover these paths.In this paper,we take advantage of static analysis to evaluate the complexity of each basic block.Then,we calculate the weights of each seed by analyzing the associated execution path extracted by Intel PT.Finally,we prioritize seed inputs with higher complexity for triggering more crashes.

Seed MutationThe crashes and paths found by fuzzers may vary significantly depending on their seed mutation strategies.Currently,AFL employs some random and seed splicing mutation operations,such asbitflip,interest,insertion,etc.However,only the mutation on a few key positions would affect the control flow of the execution.To locate these positions and then adopt optimal mutation operations,VUzzer[14]employs static and dynamic analysis to infer the input values that may affect the control flow.Then,it mutates these recognized values with appropriate offsets to meet branch conditions.Similarly,TIFF[15]adopts bug-directed mutation by inferring the type of the input bytes.FairFuzz[26]identifiers and mutates rare branches with lightweight program analysis.In this paper,we allocate more mutation energy to the seed inputs that could trigger the execution path with high complexity.In this way,there is a higher probability for our method to find more vulnerabilities.

Code CoverageCode coverage is an important indicator for the coverage-based fuzzing.It could guide the fuzzer to reveal more branches.To measure the code coverage,AFL instruments a random ID for each basic block at compile time and utilizes a 64KB shared memory(namely bitmap)to record edge coverage information.Figure 2 shows how AFL updates the bitmap.For each executed edge,AFL updates the corresponding bitmap position that is calculated by the XOR operation with the source ID and the destination ID.To fuzz binary programs and avoid the hash collision caused by random IDs,PTfuzz employs Intel PT to extract the execution path.Then,it takes the memory address of each basic block as a unique ID to update the bitmap.Inspired by PTfuzz,in this paper,we adopt Intel PT to extract the execution path and then measure the code coverage as well.Moreover,we import the fuzzer’s bitmap to the concolic execution to avoid generating the seed inputs that cover the duplicated execution paths.

2.2 Symbolic Execution

Although fuzzing has made good progress in vulnerability discovery,it still suffers from limitations in discovering bugs that are hidden deep in the execution path due to some complex branch conditions.To address this problem,symbolic execution[27,28]constructs inputs that satisfy the path constraints by taking symbolic values as program inputs and then representing branch conditions as symbolic expressions[29,30].After solving these symbolic expressions,the symbolic execution can generate new seed inputs that could explore multiple execution paths.

Unfortunately,classical symbolic execution fails to explore some feasible execution paths that contain dynamic libraries.To cope with this issue,the concolic execution is proposed.This technique combines symbolic execution and concrete execution to explore the execution paths.When the concrete execution takes a branch,the symbolic execution extracts the corresponding constraints and then solves the constraints for exploring a different branch.Moreover,to take the respective advantages of the concolic execution and the fuzzing,the hybrid fuzzing combines these two techniques.The concolic execution is used to generate seeds that satisfy branch conditions while fuzzing is used to mutate and verify these seeds quickly.With the help of hybrid fuzzing,Driller[17]identifies the same number of vulnerabilities with the winning team of the DARPA Cyber Grand Challenge.QSYM[11]implements a fast concolic execution engine by exploiting the Intel PIN to analyze each instruction at runtime.Moreover,it utilizes some heuristics to solve the path constraints.By using the hybrid fuzzing,QSYM finds more bugs than the state-of-the-art fuzzers.

However,QSYM employs a similar seed selection strategy with AFL.It prioritizes seed inputs with new branches and smaller file sizes.In this paper,we consider the CEW of each seed input on the top of QSYM.On the other hand,inspired by Driller,we prioritize seed inputs that may get stuck due to the complex branch conditions,which could help the fuzzer go through branch conditions faster and explore more execution paths.

III.OVERVIEW

In this paper,there are two problems that we mainly try to solve.One is to reduce the blindness of fuzzing,and the other is to improve the synergy between fuzzing and concolic execution.For this purpose,the key idea of our approach is to take advantage of static analysis to assist fuzzing in terms of the seed prioritization and the power scheduling,and meanwhile to assist the concolic execution to select an appropriate seed input.Figure 3 presents a high-level overview of SHFuzz.It consists of three components:static analyzer,fuzzer,and concolic execution.

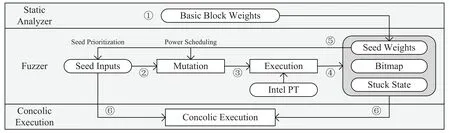
Figure 3.An overview of SHFuzz.

Static Analyzer:Static analysis is the first step of SHFuzz to evaluate the complexity and vulnerability risk of each basic block in the target binary program.Our method utilizes the IDA Pro to get the assembly code of the target program and then calculates the weights of each basic block.Since fuzzing and concolic execution are good at exploring different execution paths,we consider both the fuzzing weight(FW)and the concolic execution weight(CEW)for path exploring.The FW focuses on the complexity of basic blocks while the CEW focuses on the instructions related to path constraints.

Fuzzer:Our main fuzzing loop follows the basic workflow of PTfuzz.It starts with initial seed inputs and tries to generate new useful inputs that could increase the code coverage.For each new seed input,the fuzzer executes it and exploits Intel PT to extract the associated execution path.This path can help the fuzzer to update the code coverage and decide whether a seed input should be kept or discarded.On the other hand,it can be used to calculate the seed weights by analyzing all basic blocks’ weights inside this path.Based on the seed weights,the fuzzer can perform seed prioritization and power scheduling when choosing the next input.In general,the seed inputs with higher weights will be selected first and allocated more mutation energy.

Concolic Execution:The concolic execution is used to drive a program to go through complex branch conditions.It first takes seed inputs with higher CEWs or stuck states from the seed queue.Then,it tries to generate new seed inputs by extracting and solving the associated path constraints.To improve the synergy between fuzzing and concolic execution,we import the fuzzer’s bitmap to the concolic execution.

In general,the steps of our method can be summarized as follows:

Step 1:We take advantage of static analysis to calculate the weights of each basic block by scanning the assembly code of the target program.

Step 2:The fuzzer takes seed inputs from the seed queue and then generates new seed inputs by various mutations.

Step 3:For each new seed input,the fuzzer executes it and then exploits Intel PT to extract the associated execution path.

Step 4:Based on the execution path,the fuzzer updates the coverage bitmap and then calculates the FW and CEW of the seed related to this path.Moreover,the fuzzer marks a seed as the stuck state when it generates fewer useful seed inputs based on this seed.

Step 5:The fuzzer performs seed prioritization and power scheduling based on the seed weights.A seed input with higher FWs will be selected first and allocated more mutation energy.

Step 6:The concolic execution prioritizes seeds with higher CEWs or stuck states from the seed queue.Moreover,we import the fuzzer’s bitmap to the concolic execution for improving the synergy between fuzzing and concolic execution.

IV.DESIGN

In this section,we present the design details of our hybrid fuzzing system SHFuzz from three parts:static analyzer,fuzzer,and concolic execution.

4.1 Static Analyzer

The static analyzer disassembles the target binary program and then scans the assembly code to evaluate the complexity and vulnerability risk of each basic block.Since fuzzing and concolic execution are good at exploring different execution paths,we employ the fuzzing weight(FW)and the concolic execution weight(CEW)for hybrid fuzzing.

Fuzzing Weight.To evaluate the FW,we take advantage of two complexity metrics inspired by Cerebro[12],namely McCabe’s Cyclomatic Complexity(CC)[31]and Halstead Complexity Measures(H.B)[32].As shown in Equation(1),CC is calculated by the number of edges and basic blocks in a function,and it reflects the structural complexity.As shown in Equation(2),H.B is calculated by the number of operators and operands in a function.This metric reflects the operation complexity.In general,only certain basic blocks in a function will be executed.Therefore,CC and H.B metrics are coarse-grained.To improve the accuracy,different from the previous method[12],we divide the CC and H.B metrics by the number of basic blocks in the associated function and take the results as each basic block’s complexity weight.

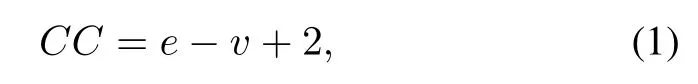
whereeis the number of edges in a function,vis the number of basic blocks inside the same function.

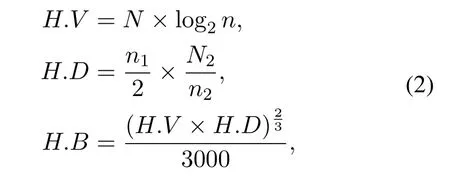
whereN=N1+N2,N1is the total number of operators,N2is the total number of operands,andn=n1+n2,n1is the total number of unique operators,n2is the total number of unique operands.

In addition,we consider the Vulnerable Library Function(VLF)metric,which is calculated by counting the times that some vulnerable library functions(e.g.,strcpy,strcat,memcpy)are invoked in a function.Inspired by the method[1],all banned functions listed in the Microsoft secure development lifecycle concept[33]will be considered as vulnerable functions.Similar to the H.B and CC,we divide the VLF metric by the number of basic blocks in the associated function and then take the result as the VLF score of each basic block.

After calculating the CC,H.B,and VLF score of each function,we use the following formula to normalize each metric,which can eliminate the effects of different magnitudes:

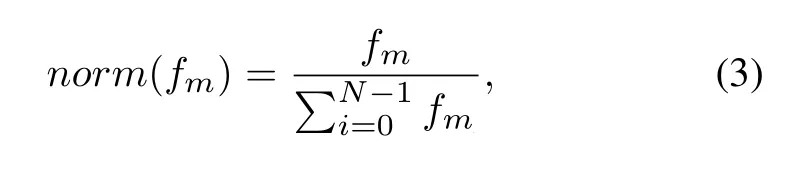
wherefmis the score of a function about the metricm,Nis the number of functions inside a program.

After that,we calculate the FW of each basic block with the following equation:

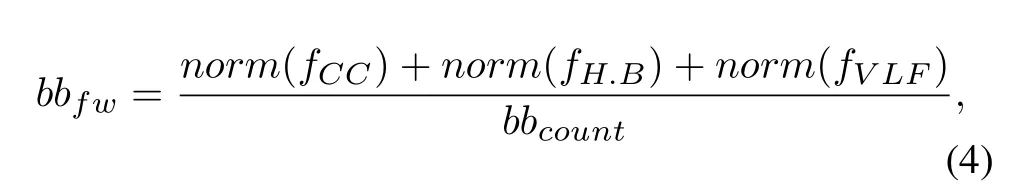
wherebbfwdenotes the FW of a basic block in the functionf,bbcountis the number of basic blocks in this function.

By first evaluating the complexity of each function and then calculating the average value,each basic block in the same function has the same FW.In this way,our method can not only reflect the structure complexity of basic blocks,but also avoid the fuzzing process skipping some simple basic blocks in a function.Our method could keep balance between the accuracy and availability of weight calculation.Different execution paths will pass through different functions and different number of basic blocks in the same function,resulting in different path complexity.

Concolic Execution Weight.The CEW mainly focuses on instructions associated with the path constraints,such as conditional jump instructions and assignment instructions.Specifically,we exploit the ABC complexity metric[1]to evaluate CEW,which is calculated by the following formula:

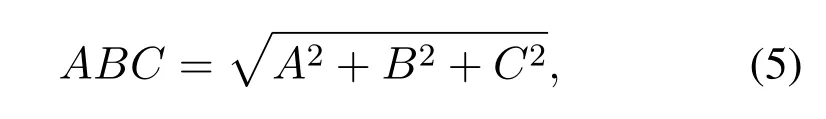
whereAis the number of assignment instructions,Bis the number of branch instructions,andCis the number of call instructions.

From Equation(5),we can observe that the ABC metric is calculated by the number of assignment instructions,jump instructions,and call instructions.Since concolic execution is not good at handing library function calls,we only consider the assignment and jump instructions when calculating the ABC metric.After getting the ABC score of each function,we adopt the Equation(6)to calculate the CEW of each basic block:

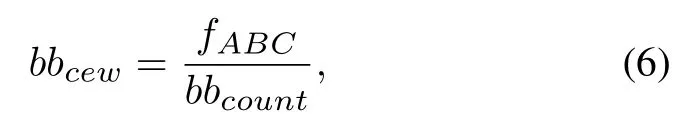
wherebbcewdenotes the CEW of a basic block in the functionf,bbcountis the number of basic blocks in this function.

4.2 Fuzzer

Algorithm 1 shows the main fuzzing loop of SHFuzz.It follows the basic workflow of PTfuzz,which starts with initial seeds and tries to generate new useful inputs.In general,our main fuzzing loop can be divided into four parts:path extraction(Line 5,15),weight calculation(Line 7,18),seed prioritization(Line 11),and power scheduling(Line 12).

Algorithm 1:The main fuzzing loop.Input:(i)Target binary program:P;(ii)Initial seeds:S;(iii)Basic blocks’weights:W;1 begin 2Q ←−∅;//Initialize the seed queue Q 3B ←−∅;//Initialize the bitmap 4for s∈S do/＊Initialize initial seeds ＊/5path=PathExtraction(P,s);6UpdateBitmap(path,B);7fw,cew=GetWeights(path,W);8PushQueue(Q,s,fw,cew);9end 10while In the fuzzing loop do 11seed=SeedPrioritization(Q);12energy=PowerScheduling(seed);13for i from 1 to energy do 14seed’=Mutation(seed);15path=PathExtraction(P,seed’);16if HasNewBranches(path,B)then 17UpdateBitmap(path,B);18fw,cew=GetWeights(path,W);19PushQueue(Q,seed’,fw,cew);20end 21end 22end 23 end

Path Extraction.When fuzzing a program,we need to extract the complete execution path for updating the bitmap and then calculate the FW and the CEW.Inspired by PTfuzz,we utilize Intel PT to recover the execution path for each execution.When Intel PT is enabled,the CPU can record the execution control flow of a target program with a minimum performance overhead.Specifically,it collects the runtime control flow information and then stores it into the specified memory space in the form of compressed PT packets.By decoding these PT packets,we can extract the complete execution path that is comprised of a series of basic blocks(Line 5,15).Based on the execution path,SHFuzz can update the code coverage bitmap for evaluating whether the seed is useful or not(Line 6,16,17).On the other hand,the execution path will be used to calculate the weights of each seed by accumulating all basic blocks’ weights(Line 7,18).

Weight Calculation.Similar to the weights of each basic block,there are two types of weights for each seed:FW and CEW.The FW is calculated by accumulating all basic blocks’FWs associated with an execution path(Line 7,18).The CEW is calculated by accumulating all basic blocks’CEWs associated with the same execution path(Line 7,18).Based on the FW of a seed,our fuzzer performs seed prioritization and power scheduling when choosing the next seed to mutate.Similarly,the concolic execution engine first selects the seeds with higher CEWs to generate new testcases.Moreover,to avoid the basic blocks in the loop being frequently calculated,we employ the exponential back-off algorithm to prune these frequent basic blocks.This algorithm only calculates basic blocks whose execution times are a power of two.Since the weight calculation is time-consuming,and it could slow down the fuzzing speed,we only calculate the weights for the seed inputs that trigger new branches(Line 16).

A motivating example.Figure 4 shows a simple example to illustrate how to calculate the path weight based on the complexity of each basic block.We can observe that there are a total of 5 paths,which are denoted asP1,P2,P3,P4andP5,respectively.Each path corresponds to a test case.By exploiting the Intel PT mechanism,we can get the sequence of basic blocks associated with each path.Then,we calculate the FW and CEW of each path by accumulating all basic blocks’FWs and CEWs associated with this path.As a result,the fuzzing weights of 5 paths are 24.70,22.43,8.67,22.30 and 30.56,respectively.Their concolic execution weights are 28.67,25.82,9.42,14.14 and 18.07,respectively.Next,we choose the test case corresponds toP5,which has the maximum FW,as the next seed for fuzzing.Meanwhile,we select the test case corresponds toP1,which has the maximum CEW,as the next seed for concolic execution.

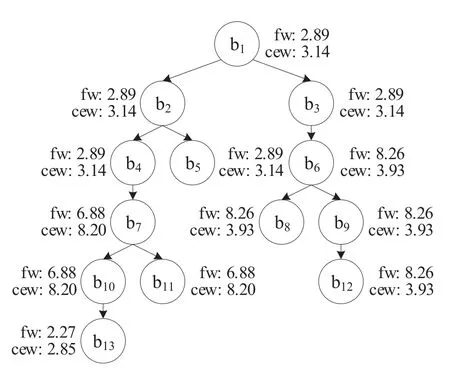
Figure 4.An example of calculating path weights.

Seed Prioritization.In general,the execution path which comes across more and complex basic blocks may have a higher chance of containing a bug.Therefore,we need to prioritize seed inputs with higher FWs for triggering more bugs.To this end,after calculating the weights of seed inputs,the fuzzer places them into the seed queue in the descending order of their FWs(Line 8,19).By doing so,the fuzzer will first pick the seed input with higher FW from the seed queue(Line 11).

Power Scheduling.For a seed input ready to be mutated,the fuzzer needs to assign mutation energy to it.This energy is used to control the times of mutation operations.A seed with higher FW should be mutated more frequently since it is more likely to trigger new paths or crashes.As a result,we utilize the following formula to assign mutation energy for each seed based on its FW(Line 12):whereenergyis the mutation energy calculated by the PTfuzz strategy,fwis the FW of the current seed input,Nis number of seed inputs in the seed queue.

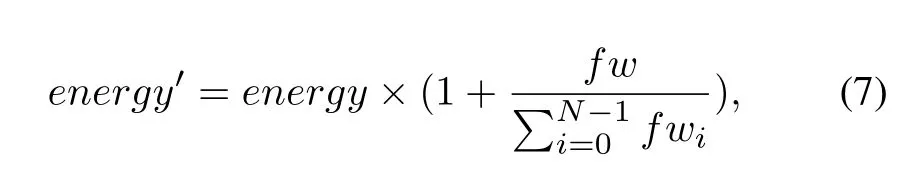
Moreover,we also count the number of useful seed inputs generated by mutating a seed input.If this number is less than half of the average calculated by all seeds,we mark this seed as a stuck state.This state indicates the mutations may be less useful to this seed.In this case,the concolic execution could help generate more interesting input seeds by solving the associated path constraints.To this end,we prioritize seeds with stuck states or higher CEWs when performing the concolic execution.

4.3 Concolic Execution

Our concolic execution engine is implemented on the top of QSYM[11].It first utilizes the Intel PIN tool to extract the execution path constraints.Then it employs the Z3 solver[34]to solve these constraints for generating new seed inputs that satisfy the complex branch conditions.With the help of the concolic execution,the fuzzer could quickly go through complex branch conditions by executing these generated input seeds.When performing the concolic execution,the seed prioritization is the first step for selecting an appropriate seed input from the fuzzer’s seed queue.

Seed Prioritization.As described in Section 4.1,the CEW indicates the complexity of instructions associated with path constraints.Accordingly,we employ the CEW as an indicator for seed selection.This weight can be extracted during the fuzzing process.On the other hand,we utilize the stuck state as another indicator.The stuck state shows a seed may get stuck during fuzzing due to some complex branch conditions.SHFuzz transfers the seeds that get stuck or have higher CEWs to the concolic execution engine at first.Then,the concolic execution engine tries to extract path constraints associated with this selected seed.After that,it generates new seed inputs to satisfy branch conditions by solving the above path constraints.Finally,the fuzzer will execute these new seed inputs and then update the code coverage bitmap.In this way,the fuzzer may have more chances to go through complex branch conditions and then trigger more paths or crashes.

Coverage Bitmap.Listing 2 is a simple code snippet taken fromnasm,which is an asssembler for the x86 CPU architecture.We take this code as a motivating example to elaborate on why we need to import the fuzzer’s bitmap to the concolic execution.The control flow graph of this code is shown in Figure 5.It contains 7 basic blocks(without considering the called functions).The green color indicates a basic block has been executed by the fuzzer.This execution information is recorded in the code coverage bitmap.If the concolic execution does not check this bitmap,it needs to extract and solve path constraints associated with the basic blocks A,C and D.However,the basic blocks A,C,and their child nodes have been executed.As a result,some seed inputs generated by the concolic execution may cover the same execution paths with the fuzzer.

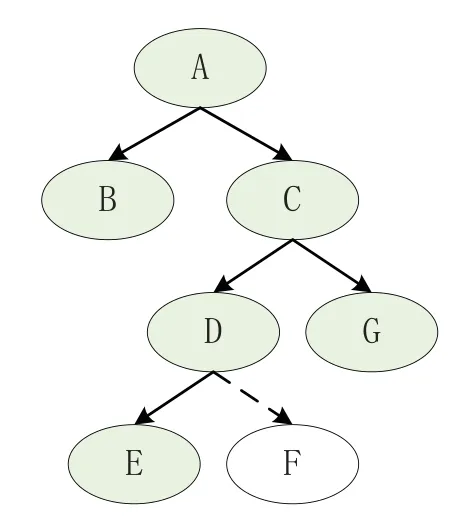
Figure 5.The control flow graph of Listing 2.

Listing 2:Sample code snippet from nasm.

To address the above issue,we import the fuzzer’s bitmap to the concolic execution.When the concolic execution engine tries to generate a seed input,it checks this bitmap at first.Specifically,for each basic block that contains the condition jump instruction,it exploits Intel PIN to extract two possible basic blocks following the condition jump.Then,we use the method shown in Figure 2 to check the corresponding bitmap indexes based on the memory addresses of the current and the next two basic blocks.If there is an edge from the current basic block to the next one not being executed,the concolic execution engine will solve the path constraints associated with this edge.In this way,only the new seed inputs will be generated,and the execution time could be reduced.

V.IMPLEMENTATION AND EVALUATION

SHFuzz is implemented on the top of PTfuzz[20]and QSYM[11],which are the popular binary-oriented fuzzer and concolic execution engine,respectively.Moreover,our static analyzer utilizes the disassembly tool(i.e.,IDA Pro)to calculate the weights of each basic block.To evaluate the weights of each seed input at runtime,we accumulate all basic blocks’ weights associated with an execution path extracted by Intel PT.Moreover,we also add the support for PTfuzz to perform seed prioritization and power scheduling based on the seed weights.To prioritize an appropriate seed input for the concolic execution,we add the support for QSYM to first select the seed inputs with stuck state or higher CEW.Moreover,we also import the bitmap of the fuzzer to the concolic execution engine for improving the synergy between fuzzing and concolic execution.

5.1 Experiment Setup

Baseline Fuzzers.To highlight the effectiveness of our method,we compare the experimental results with PTfuzz[20]and AFLFast[23].PTfuzz is a state-ofthe-art fuzzer that supports fuzzing binary programs by utilizing Intel PT.AFLFast utilizes a Markov chain model to specify low-frequency paths and then gravitates towards these low-frequency paths for exploring more paths.Like AFL,AFLFast uses QEMU mode to test binary programs.To compare with SHFuzz,we add Intel PT support for AFLFast to eliminate the influence of QEMU during experiments.

Benchmarks.First,we evaluate SHFuzz on 6 realworld applications as shown in Table 1.These applications cover a wide range of functionality and input formats,including GNU Binutils(i.e.,size,nm),image processing libraries(i.e.,jhead,libtiff),and PDF processing tool(i.e.,pdftotext).On the other hand,all these applications are well-tested by the state-of-theart fuzzers[11,16].Therefore,they are good benchmarks to demonstrate the effectiveness of our fuzzer.

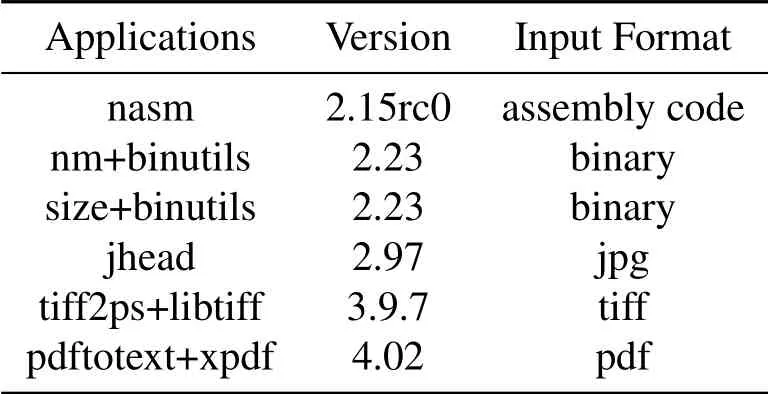
Table 1.Real-world applications used in the evaluation.

Second,we choose the LAVA-M dataset[19]as another benchmark.LAVA-M is a well-known test suite for program bug detection.It consists of four buggy programs(i.e.,who,uniq,base64,andmd5sum).Each bug is injected artificially and identified by a unique ID.Since the LAVA-M dataset contains several welldesigned bugs,many fuzzers choose it as their benchmarks.The programs included in LAVA-M have been widely evaluated as well.

Evaluation Metrics.We select unique crashes and paths as major evaluation metrics to compare the efficiency of each fuzzer.The number of unique crashes represents the fuzzer’s ability to trigger vulnerabilities.The number of unique paths represents the code coverage captured by a fuzzer.A fuzzer is more effective if it could trigger more unique crashes or paths.

Experiment Environment.For each program under test,we employ PTfuzz,AFLFast-PT and SHFuzz on it for 24 hours.Then,we compare the effectiveness of different strategies.Moreover,all experiments are conducted with the same initial seed inputs on a machine with one Intel i7-9700K CPU and 32GB RAM running 64-bit Ubuntu 16.04 system.

5.2 Evaluation on Real-world Applications

To show the effectiveness of our hybrid fuzzing strategy assisted by static analysis,we first conduct experiments on 6 real-world applications.For each application,we count the number of unique paths and crashes found by PTfuzz,AFLFast-PT and SHFuzz with the same initial seeds.To show the benefits of static analysis and concolic execution respectively,we conduct experiments on two cases:SHFuzz without concolic execution and SHFuzz with concolic execution.

Table 2 shows the experiment results of PTfuzz,AFLFast-PT and SHFuzz on 6 real-world applications.For the case of SHFuzz without concolic execution,SHFuzz discovers 15521 unique paths and 1047 unique crashes while PTfuzz finds 15156 unique paths and 778 unique crashes in total.SHFuzz outperforms PTfuzz on all applications in terms of the number of crashes,which increases by 34.58% over PTfuzz.Specifically,compared with PTfuzz,SHFuzz discovers 150%and 120%more unique crashes onsizeandtiff2ps,respectively.Since SHFuzz pays more attention to more complex basic blocks,it finds fewer paths onnasmandtiff2psthan PTfuzz.In general,SHFuzz could discover more unique crashes on all applications and more unique paths on the other 4 applications than PTfuzz.Compared with AFLfast-PT,SHFuzz without concolic execution discovers more unique paths but few unique crashes in total.It outperforms AFLfast-PT onnmandjhead,and could find more unique crashes onnasm,size,andtiff2ps.It also discovers more paths onpdftotext.Since the run-time weight calculation is time-consuming,it may slow down the speed of finding unique paths onnasm,size,andtiff2ps.However,SHFuzz can discover more unique crashes on 4 applications than AFLFast-PT.As a conclusion,with the help of static analysis,SHFuzz can discover more unique crashes,which demonstrates its effectiveness in vulnerability discovery.

For the case of SHFuzz with concolic execution,SHFuzz finds more unique paths and crashes than PTfuzz and SHFuzz(without concolic execution)in total,but it finds fewer crashes than AFLFast-PT.Specifically,SHFuzz could find more unique paths and crashes than PTfuzz on all applications,and it discovers more unique crashes than the case of SHFuzz without concolic execution on 4 applications(but except fortiff2psandpdftotext).Moreover,SHFuzz discovers more paths on all applications and more crashes on 4 applications than AFLFast-PT.In particular,with the help of concolic execution,SHFuzz finds 53 unique crashes onjheadwhile the other three fuzzers do not find any crashes.Compared with the other three fuzzers,SHFuzz finds more than twice as many unique paths onjhead,and more than twice as many unique crashes onsize.It is worth noting that one of our finding bugs has been assigned a CVE ID(i.e.,CVE-2019-20352).However,SHFuzz finds fewer unique crashes ontiff2psandpdftotext.The potential reason is that the concolic execution engine could drive the fuzzer to reach more execution paths,which may not contain the vulnerabilities to cause crashes.

To further demonstrate the effectiveness of SHFuzz,we track the growth trend of the number of unique crashes explored in 24 hours,which is presented in Figure 6.From this Figure,we can see that SHFuzz outperforms PTfuzz on all applications eventually.We can also find SHFuzz outperforms AFLFast-PT on 5 applications exceptpdftotext.The unique crashes found by PTfuzz and AFLFast-PT will grow rapidly at first,but they get stuck or slow down after a while,especially onnm,size,andtiff2ps.Moreover,the number of unique crashes discovered by SHFuzz with concolic execution obviously increases innmandsizeat a time.The reason is that the concolic execution engine generates some new useful seed inputs.These inputs could satisfy the path constraints and drive the fuzzer to go through deep paths and trigger more crashes.However,compared with the case of SHFuzz only assisted by static analysis,the concolic execution is not effective ontiff2psandpdftotext.The potential reason is that the additional execution paths found by the concolic execution may not contain the vulnerabilities.

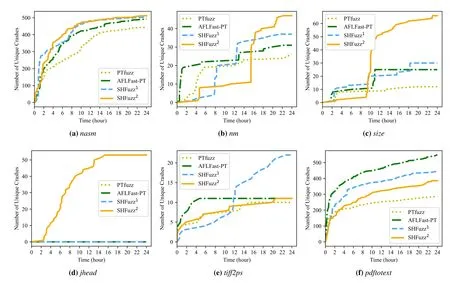
Figure 6.Number of unique crashes discovered by PTfuzz,AFLFast-PT and SHFuzz over time in 24 hours.In this Figure,SHFuzz1 represents SHFuzz(without concolic execution),and SHFuzz 2 represents SHFuzz(with concolic execution).

Furthermore,to evaluate the benefit of our strategy for concolic execution,we conduct experiments of PTfuzz + QSYM and SHFuzz(without concolic execution)+QSYM.The suffix”+QSYM”means that PTfuzz and SHFuzz(without concolic execution)are assisted by the original QSYM strategy without considering the CEW and the fuzzer’s bitmap during concolic execution.In contrast,SHFuzz(with concolic execution)is assisted by the modified QSYM with the help of our strategy based on the CEW and the fuzzer’s bitmap.The experimental results are shown in Table 3.In general,with the help of QSYM,PTfuzz and SH-Fuzz could find more paths and unique crashes.On the other hand,our strategy(i.e.,SHFuzz with concolic execution)outperforms PTfuzz+QSYM and SHFuzz(without concolic execution)+ QSYM onnasm,nm,sizeandjheadprograms.However,it discovers less paths than PTfuzz + QSYM and less crashes than SHFuzz(without concolic execution)+ QSYM ontiff2ps,and discovers less paths and crashes than SHFuzz(without concolic execution)+QSYM onpdftotext.A possible reason is that CEW is calculated by the number of assignment instructions and jump instructions,which would drive concolic execution go through paths with multiple assignments and jumps.However,these paths in some programs(e.g.,tiff2psandpdftotext)may have complicated path constraints,which could decrease the speed of concolic execution to find more unique paths or even cause concolic execution to fail resolving the paths.As a conclusion,different strategies may have different effectiveness for different programs and there is no grand slam that canbeat others,which has been demonstrated by the recent work[35].

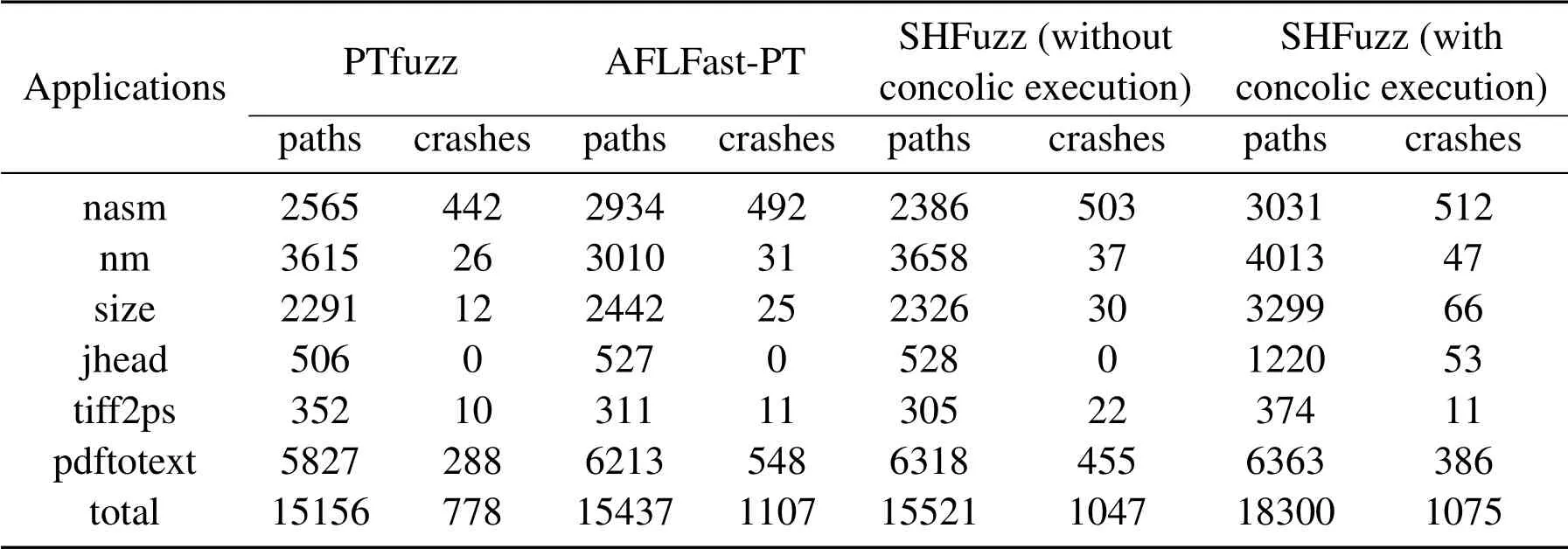
Table 2.The unique paths and crashes found by PTfuzz,AFLFast-PT and SHFuzz on 6 applications.

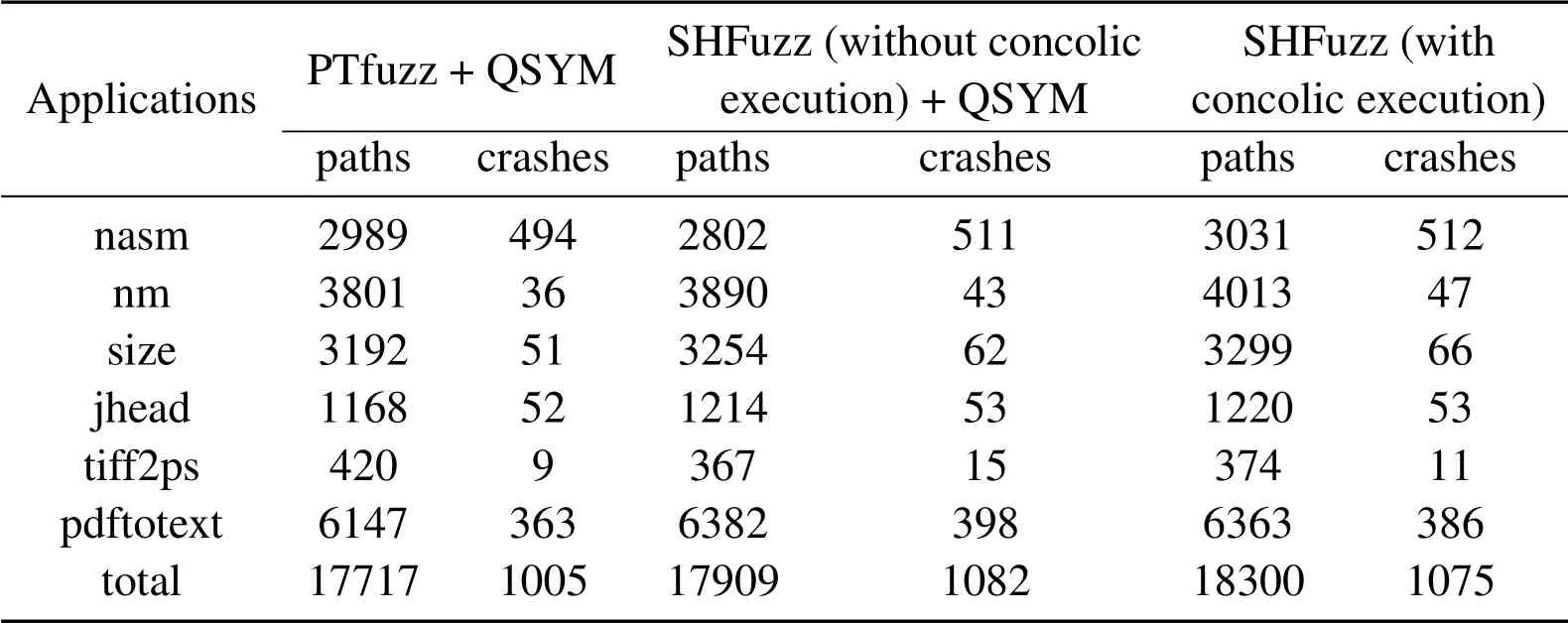
Table 3.The unique paths and crashes found by PTfuzz and SHFuzz with QSYM on 6 applications.

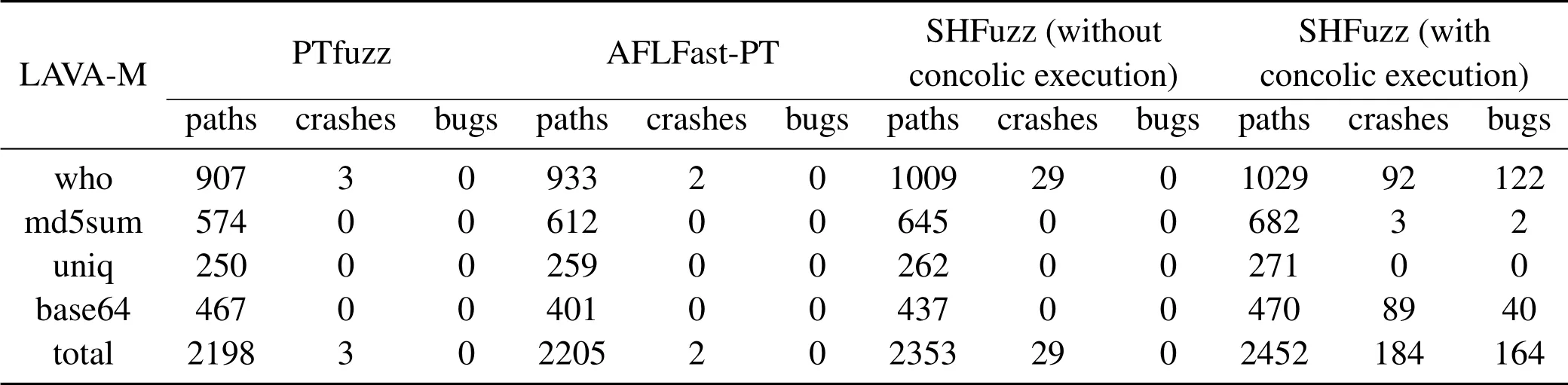
Table 4.The unique paths,crashes and bugs found by PTfuzz,AFLFast-PT and SHFuzz on LAVA-M.

5.3 Evaluation on LAVA-M

To further evaluate the effectiveness of our proposed SHFuzz,we also compare it with PTfuzz and AFLFast-PT on the LAVA-M dataset[19],which consists of four buggy programs(i.e.,who,uniq,base64,andmd5sum).We run PTfuzz,AFLFast-PT,SHFuzz(without concolic execution),and SHFuzz(with concolic execution)on these four buggy programs for 24 hours with the same settings.Then,we count the number of unique crashes and paths found on each program.

As shown in Table 4,with the help of static analysis,SHFuzz(without concolic execution)discovers more unique paths and crashes than AFLFast-PT on all applications.It also finds more unique paths than PTfuzz onwho,md5sum,anduniq.Specifically,SHFuzz(without concolic execution)discovers 1009,645,and 262 unique paths onwho,md5sum,anduniqwhile PTfuzz finds 907,574,and 250 unique paths,which increases around 11.25%,12.37%,and 4.80%,respectively.Particularly,SHFuzz(without concolic execution)discovers 29 unique crashes onwhowhile PTfuzz finds 3 crashes and AFLFast-PT finds 2 crashes.However,PTfuzz outperforms SHFuzz onbase64since SHFuzz pays more attention to fuzzing more complex basic blocks rather than tries to improve the code coverage.

Table 5.The unique paths,crashes and bugs found by SHFuzz with two different concolic execution strategy on LAVA-M.

With the help of concolic execution,SHFuzz finds 2452 unique paths and 184 unique crashes in total.It discovers 4.21% more unique paths and 534.48%more unique crashes when compared to SHFuzz without concolic execution.In particular,SHFuzz finds 3 and 89 unique crashes onmd5sumandbase64respectively while PTfuzz,AFLFast-PT and SHFuzz(without concolic execution)do not find any crashes in these programs.Moreover,SHFuzz finds 92 unique crashes onwhowhile PTfuzz,AFLFast-PT and SHFuzz(without concolic execution)find 3,2 and 29 unique crashes,respectively.Furthermore,SHFuzz discovers more unique paths than PTfuzz and AFLFast-PT on all programs.However,SHFuzz does not discover any crashes onuniq.A possible reasonis that the fuzzer could not provide appropriate seed inputs to the concolic execution to generate useful inputs.

Since each bug in LAVA-M is identified by a unique ID,we also count the number of unique bugs found by each fuzzer by further analyzing their corresponding crashes.In total,there are 2136,57,28,44 bugs inwho,md5sum,uniqandbase64,respectively.As shown in Table 4,SHFuzz with concolic execution finds 122,2,0,and 40 bugs inwho,md5sum,uniq,andbase64,and the other three fuzzers do not discover any bugs.With the help of concolic execution,SHFuzz could find 5.71%,3.51%,0%,90.91%of all bugs inwho,md5sum,uniq,andbase64,respectively.However,our path complexity strategy and AFLFast’s strategy based on path execution frequency do not play a significant role in bug discovery.This is because every bug in LAVA-M is artificially injected,and concolic execution is good at dealing with them while traditional fuzzing methods are difficult to locate these bugs.

To evaluate the effectiveness of our strategy for concolic execution on LAVA-M,we also conduct experiments of SHFuzz(without concolic execution)+QSYM.The experiment results are shown in Table 5.From this table,we can see that with the help of QSYM,SHFuzz(without concolic execution)could find more paths and crashes on all LAVA-M programs than before.Moreover,it also finds more paths onwho,md5sumanduniqprograms than SHFuzz(with concolic execution).However,our concolic execution strategy based on the CEW and the fuzzer’s bitmap could find more crashes and bugs onwhoandmd5sum,and equal crashes onuniq.The results show that our strategy could be generally more effective for discovering vulnerabilities.For thebase64program,our strategy finds more paths but less crashes than SHFuzz(without concolic execution)+QSYM.A potential reason is that our strategy drives thebase64program to reach more execution paths,which may not contain crashes and bugs.

VI.DISCUSSIONS AND LIMITATIONS

SHFuzz has some limitations that need to be improved.First,since we need to calculate the seed weights at runtime,it could slow down the fuzzing speed.To reduce this overhead,SHFuzz only calculates weights for seed inputs that trigger new branches.Second,we first measure the complexity of each function and then take the average value as the complexity of each basic block.Although this method could reflect the structure and VLF information of basic blocks,and avoid some simple basic blocks being ignored,it may not be so fine-grained and accurate for computing the complexity of a basic block.To address this issue,a more accurate complexity calculation method could be studied in our future work.Third,we calculate the seed weights by accumulating the weights of all basic blocks on the associated execution path.This calculation method favors larger seed inputs because they may contain more basic blocks.To balance the weight and file size of a seed input,a possible solution is to prioritize seed inputs based on more comprehensive metrics.Moreover,we just allocate more mutation energy for seeds with higher fuzzing weights,which can be improved by utilizing some heuristic algorithms to choose optimal mutation operations.Since the symbolic execution is limited to solve the complex path constraint in large-scale applications,a more advanced combination scheme between fuzzing and concolic execution is needed for hybrid fuzzing.

VII.CONCLUSION

In this paper,we present SHFuzz,a hybrid fuzzing system assisted by static analysis for testing binary programs.The basic idea of SHFuzz is to perform seed prioritization and power scheduling based on the fuzzing and concolic execution weights of seed inputs.Additionally,SHFuzz records the stuck seed inputs and imports the fuzzer’s coverage bitmap to the concolic execution to improve the efficiency and effectiveness of the hybrid fuzzing.Our evaluation results show SHFuzz could discover more unique crashes on the real-world applications and the LAVA-M dataset when compared to the previous solutions.

ACKNOWLEDGEMENT

This work was supported in part by the National Key Research and Development Program of China under Grant No.2016QY07X1404,National Natural Science Foundation of China(NSFC)under Grant No.61602035 and 61772078,Beijing Science and Technology Project under Grant No.Z191100007119010,CCF-NSFOCUS Kun-Peng Scientific Research Foundation,and Open Found of Key Laboratory of Network Assessment Technology,Institute of Information Engineering,Chinese Academy of Sciences.