Two-Timescale Online Learning of Joint User Association and Resource Scheduling in Dynamic Mobile EdgeComputing

Jian Zhang,Qimei Cui,*,Xuefei Zhang,Xueqing Huang,and Xiaofeng Tao

1 National Engineering Laboratory for Mobile Network Technologies,Beijing University of Posts and Telecommunications,Beijing 100876,China

2 Department of Computer Science,New York Institute of Technology,Old Westbury,NY,11568,USA

Abstract:For the mobile edge computing network consisting of multiple base stations and resourceconstrained user devices,network cost in terms of energy and delay will incur during task offloading from the user to the edge server.With the limitations imposed on transmission capacity,computing resource,and connection capacity,the per-slot online learning algorithm is first proposed to minimize the time-averaged network cost.In particular,by leveraging the theories of stochastic gradient descent and minimum cost maximum flow,the user association is jointly optimized with resource scheduling in each time slot.The theoretical analysis proves that the proposed approach can achieve asymptotic optimality without any prior knowledge of the network environment.Moreover,to alleviate the high network overhead incurred during user handover and task migration,a two-timescale optimization approach is proposed to avoid frequent changes in user association.With user association executed on a large timescale and the resource scheduling decided on the single time slot,the asymptotic optimality is preserved.Simulation results verify the effectiveness of the proposed online learning algorithms.

Keywords:user association; resource scheduling;stochastic gradient descent; two-timescale optimization;mobile edge computing

I.INTRODUCTION

With the rapid development of Internet of Things(IoT),there is explosive growth in various computation-intensive applications,such as intelligent transportation and autonomous cars in the smart city[1–3].However,with limited computing power and battery capacity,IoT devices cannot effectively support these computation tasks locally[4–6].By bringing the computing capability closer to the edge network,mobile edge computing(MEC)is crucial to reduce the latency and energy consumption of IoT devices[7–10].With the development of ultradense networks(UDN),it is promising to implement MEC by integrating wireless access and computing functionalities in small base stations[11–14].In the UDN-enabled MEC network,computation offloading from IoT devices to multiple edge servers need to address the following challenges.

1)For each IoT device,the task offloading involves selecting the edge server(i.e.,user association)as well as allocating the communication and computing resources for the offloaded task(i.e.,resource scheduling).With multiple base stations,the joint optimization of discrete user association and continuous resource scheduling is not trivial.

2)The rich temporal and spatial variations in dynamic MEC network,such as the computing task arrived at user devices,the availability of transmission capacity,and the utilization of computing resources in different edge servers,cannot be obtained in advance.Without prior knowledge of such system dynamics,the joint decisions of user association and resource scheduling are challenging.

3)The frequent user associations and the subsequent network handover and computation migration could introduce high network overhead(i.e.,delay and energy consumption).To reduce the network overhead in practice,the user association and resource scheduling have to be optimized at different timescales.

1.1 Related Works

In recent years,the computation offloading in MEC has attracted an increasing amount of attention,but most of the previous research focused onthe offloading policy and resource allocationofsingle edge server.Maoet al.[15]proposed a joint optimization of radio and computational resources to minimize the weighted sum power consumption of the multiuser MEC system with random task arrival.In[16],an energy-efficient task offloading scheme was developed to allocate the transmit power and time slot for the non-orthogonal multiple access(NOMA)enabled MEC system with one access point.In[17],a cooperative partial computation offloading was designed for multiple users to minimize the execution delay.For the D2D-enabled MEC network,the improvement of computation capacity[18]was designed for a scenario with one edge server and multiple devices.However,by considering a single edge server,the abovementioned existing works cannot solve the problem of the edge server selection problem,i.e.,which edge server the task should be offloaded to.

Several recent studies have focused onthe computation offloading and resource allocationformultiple edge servers[19–22],with the perfect knowledge of network environment,such as channel transmission rate and available computing resource.In[19],the joint optimization of task offloading,power allocation,and computing resource allocation was studied to minimize the weighted sum of execution delay and energy consumption in the multi-server MEC network.Kanet al.[20]designed a heuristic algorithm to minimize the cost function of quality-ofservice(QoS),by deciding the task offloading and resource allocation in the multi-user multi-server scenario.In[21],based on the theory of double auction,a cost-effective pricing mechanism was considered to allocate the computing resource across multiple edge servers.In[22],a decentralized game-theoretic costeffective approach was proposed to match the mobile devices with edge servers,with the objective of increasing user connection capacity.These research are based on offline static optimization methods with a-prior complete knowledge of network environment,which are inapplicable for dynamic MEC network.

There are a few works consideringthe user associationin adynamic MEC network with temporal and spatial variations.In[23],the authors proposed a deep deterministic policy gradient(DDPG)enabling reinforcement learning method to improve the quality of experience(QoE)in live video service,by designing the policy of user association and video quality selection.In[24],by using the deep learning methods,the position planning of ground vehicles and unmanned aerial vehicles(UAVs),as well as the joint optimization of user association and resource allocation were developed to minimize the energy consumption of all users in the hybrid MEC network.However,the above user association and resource allocation are optimized on the same single timescale,without considering the high network overhead caused by handover and task migration during the frequent user associations.Moreover,the system stability of the MEC network and the spatial connection capacity among edge servers have not been considered in these works.

In our previous work[25],a Markov decision process(MDP)based task offloading algorithm was developed to minimize the average delay with the knowledge of state transition probabilities.In[26],by integrating MDP and Lyapunov optimization,an online learning proactive network association scheme was proposed to minimize the average task delay of multiple machines.However,the user association(or network association)scheme is designed with given resource scheduling in the environment.Moreover,the user association was implemented in a single timescale,i.e.,per slot or per computing task arrival.

1.2 Contributions

Motivated by the limitations of current research,we propose the asymptotically optimal per-slot online learning method to jointly optimize the user association and resource scheduling in MEC network,aiming at reducing the time-averaged operation cost of the network(e.g.,energy consumption or economic expense).Moreover,to alleviate the high network overhead caused by frequent user associations,the twotimescale online learning approach is developed to perform user association and resource scheduling on two different timescales.The main contributions of this paper are summarized as follows:

First,for the dynamic system with multiple base stations and multiple devices,the time-varying environment is considered when the user association and resource scheduling are jointly optimized to minimize the time-averaged operation cost.To the best of our knowledge,this is the first work that introduces the two-timescale online learning method to make the joint decisions of user association and resource scheduling in dynamic MEC network.

Next,by integrating the theories of stochastic gradient descent(SGD)and minimum cost maximum flow,the per-slot online learning approach of user association and resource scheduling is proposed,which can achieve the asymptotically optimal performance without requiring any prior knowledge of the network environment.

Finally,to alleviate the high network overhead caused by the frequent user associations,the generalized two-timescale online learning of user association and resource scheduling is developed while preserving the asymptotic optimality:the user association is operated on a larger timescale,and the resource scheduling is performed per time slot.

1.3 Organization

The rest of the paper is organized as follows.The system model and problem formulation are presented in Section II.The per-slot and two-timescale online learning methods of user association and resource scheduling are in Sections III and IV,respectively.In Section V,the effectiveness of the proposed algorithms is shown by simulations,followed by conclusions in Section VI.

II.DYNAMIC MEC FRAMEWORK

2.1 System Model

As shown in Figure 1a,we consider a dynamic MEC network consisting ofM={1,··· ,M}IoT devices andN={1,··· ,N}small base stations(SBSs),each of which is equipped with one edge server.At any time slott,the network topology can be denoted by a bipartite graphG(t)=< M,N,E(t)>,whereE(t)={eij(t),∀i∈M,∀j∈N}is the edge set between the device verticesMand the server verticesN.At timet,if thei-th device is within the coverage of edge serverj,the binary indicatoreij(t)is set as 1,and 0 otherwise.

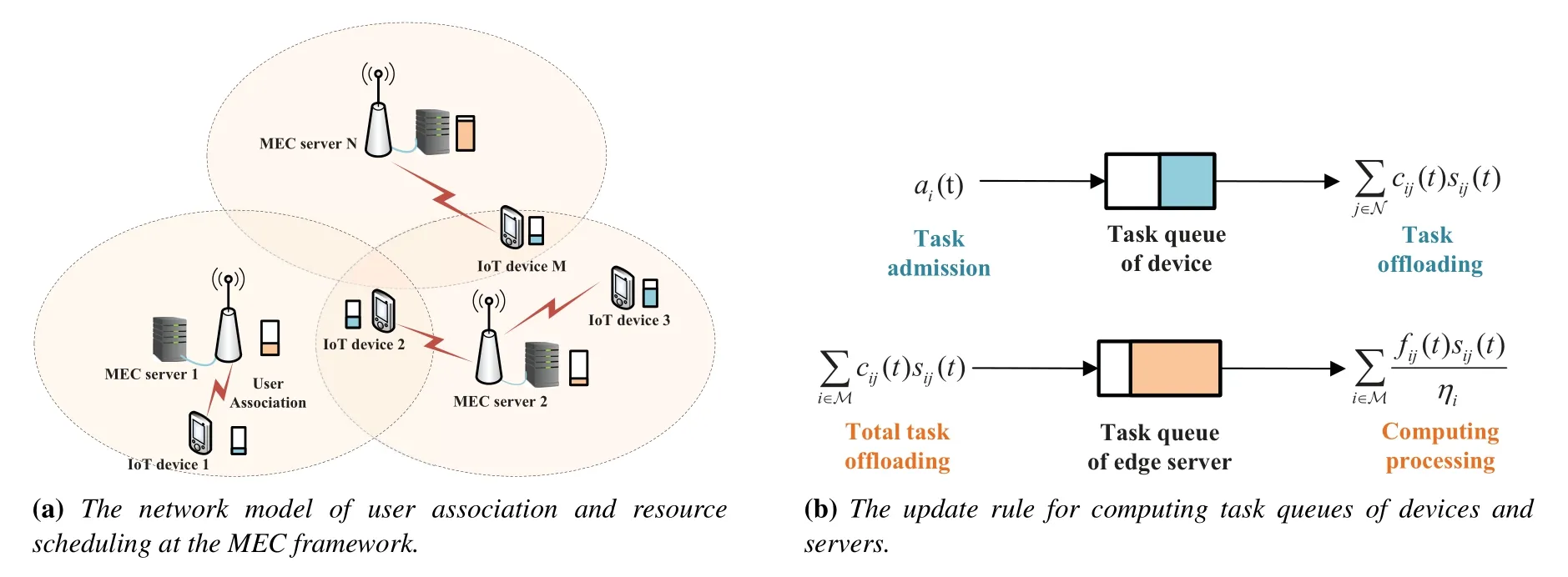
Figure 1.The dynamic MEC scenario consisting of multiple base stations(i.e.,edge servers)and multiple IoT devices.

Since the coverage areas of SBSs can overlap,sij(t)is defined as the instantaneous user association indicator between deviceiand serverj.The following constraints are imposed on the binary user association indicatorsij(t):

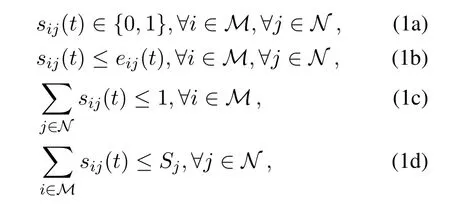
where constraint(1a)implies the binary user association indicator will be 1 only when the computing task of deviceiis offloaded to serverj.(1b)indicates that each server can only accept tasks offloaded by the users within coverage.Constraint(1c)means that deviceican be associated with at most one base station(i.e.,edge server)[27,28].Constraint(1d)is the constraint of connection capacity on serverj,whereSjis the maximum number of devices that can be connected to serverjin each slot.It is challenging for each device to connect to multiple servers,the computing task has to be processed in parallel[29],the device has to be able to have strong wireless connection to multiple base stations[30],etc.For the IoT device being simultaneously associated to multiple base stations or edge servers,interesting future research such as cooperative transmission and computing processing between edge servers can be considered,but out of the scope of this paper.

In thei-th device,the computing tasks can be represented as a tuple(ai(t),ηi),whereai(t)is the size of tasks admitted into the queue at timetin units of bits,the computing intensityηispecifies the number of CPU cycles needed to process one bit of computing task.The task admission satisfies:

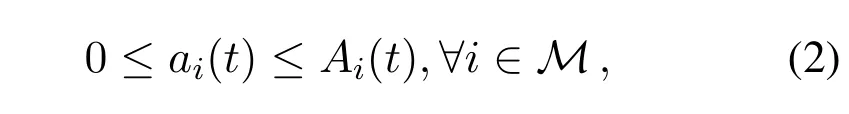
whereis the size of tasks arrived at thei-th device at timet,andis limited by the buffer size of the device.The constraint(2)means that the task admission in slottcannot exceed the task arrival.

During thet-th time slot,defineas the transmission capacity of edge serverjin terms of bits.is the upper bound imposed by the total amount of available communications resources.Letcij(t)denote the size of the computing task offloaded from deviceito serverj,and we have:

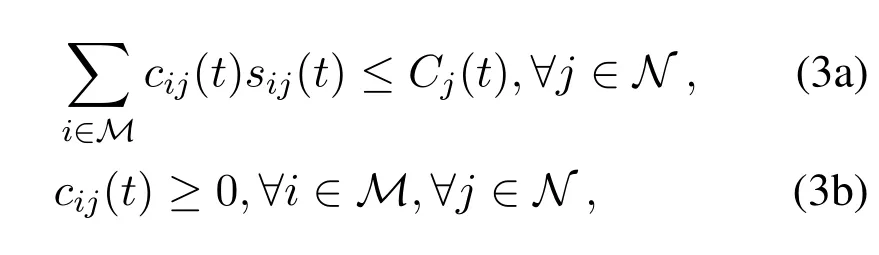
where the constraint(3a)indicates that the total amount of computing task offloaded to the edge serverjcannot exceed its transmission capacity,and(3b)specifies the non-negativity of task offloading.

SupposeFj(t)is the total available computing resource of serverjat slott,andwhereis the maximum number of CPU-cycles equipped at serverj.The number of CPU-cycles allocated by serverjto process the computing task offloaded from deviceiat slottis defined asfij(t).Similarly,the computing resource allocation has to satisfy the following conditions:

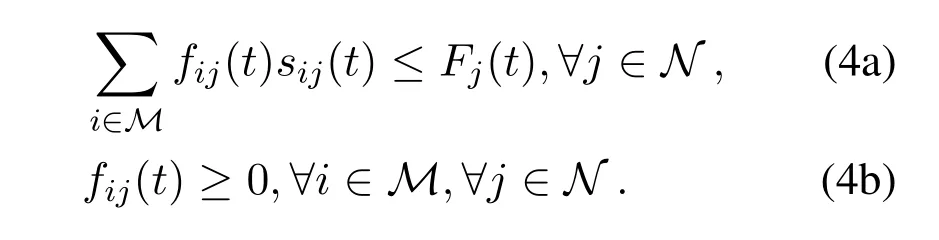
The above constraints are similar to(3a)and(3b),indicating the finiteness and non-negativity of computing resources.

In the dynamic edge computing network,the size of computing tasks to be processed at the devices and edge servers are quantified as queue status,where the computing tasks in the queue can be offloaded or processed according to the first-in-first-out(FIFO)rule,as shown in Figure 1b.LetQi(t)andGj(t)denote the queue backlog of computing tasks(in terms of bits)on deviceiand serverj,respectively,which will update as follows.

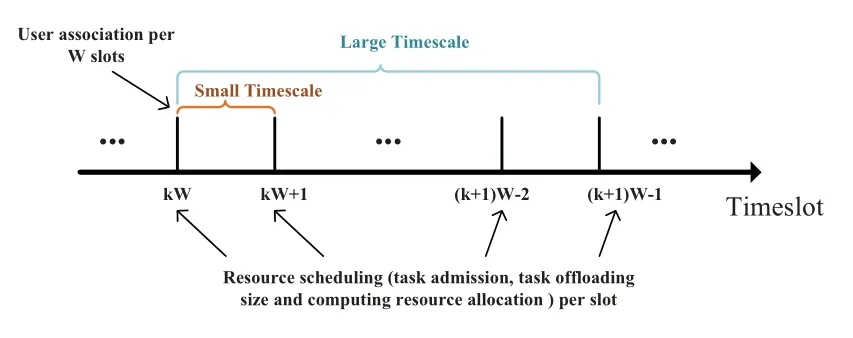
Figure 2.The two-timescale optimization framework.

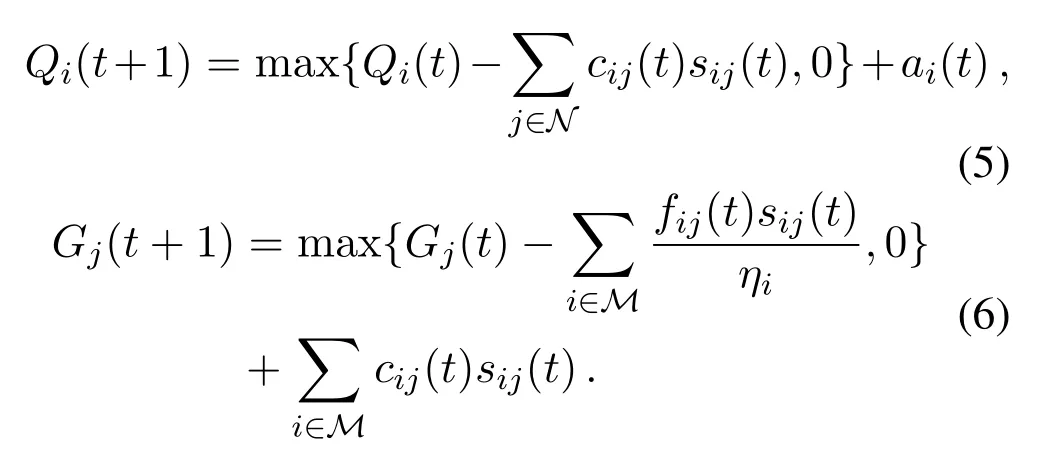
Eqs.(5)–(6)show how the instantaneous queue status updates from timetto time(t+1).For Eq.(5),the first term is the size of computing task remaining at deviceiat slott,after subtractioncij(t)sij(t)amount of computing task being offloaded to its associated edge serverj.The second term is the newly arrived computing task at timet.Similarly,the first term on the right side of(6)is the size of computing task available at serverjat slott,after subtractionfij(t)sij(t)/ηiamount of computing task being processed.The second term is the size of the computing tasks being newly offloaded from its associated devices.

2.2 Problem Formulation

At time slott,the generic operation cost(such as energy consumption or economic expense)of the MEC network[31]depends on variables including task admission,user association,task offloading,and computing resource allocation.

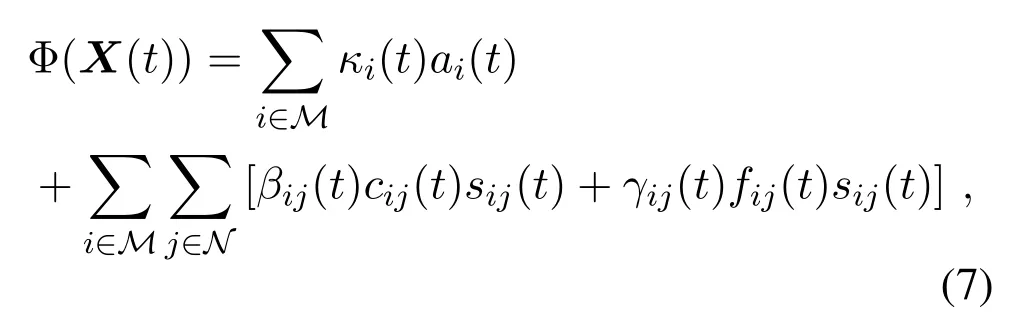
whereX(t)={ai(t),sij(t),cij(t),fij(t),∀i∈M,∀j∈ N},andκi(t),βij(t)andγij(t)are the per-unit operation cost of task admission(bit),task offloading(bit),and computing allocation(CPU-cycle).

For the duration overT={0,··· ,t,··· ,T −1}time slots,the problem of interest is to minimize the long-term time-averaged operation cost with the consideration of system stability in terms of queues,i.e.,

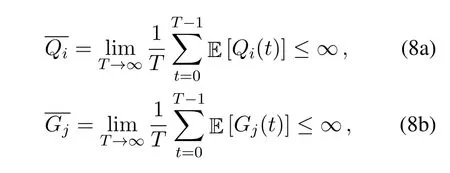
which means that the computing task queues of devices and edge servers in the dynamic edge network should meet strong stability[32].The time-averaged operation cost can be given as

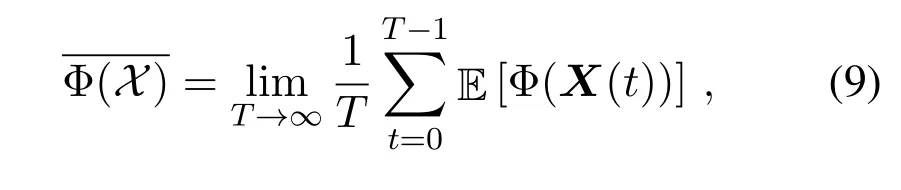
whereX={X(0),··· ,X(T −1)}collects the variables inX(t)across all time slots.

With the above definitions,the operation cost minimization problemis formulated as

The above problem is the joint optimization of user association and resource management,where the optimization variables include user association,task admission,task offloading(i.e.,wireless resource),and computing resource.The constraints of Eq.(10)are given listed as follows:(1)for user association;(2)–(4)for the limitations on task admission,wireless resource and computing resource; and(8)for the requirements of system stability in dynamic MEC network.The detailed explanation of the constraints can refer to the above Eqs.(1)–(4),and Eq.(8).

The above problem is highly challenging due to the time-averaged objective function and constraints,the optimum of(10)requires a-priori knowledge of time-varying random processes(i.e.,Ai(t),Cj(t)andFj(t))in MEC network.This is impractical due to the violation of causality.Furthermore,the constraint(1d)makes the optimal decision of user association spatially coupled due to the different connection capacities of edge servers in various geographic locations.

III.PER-SLOT ONLINE LEARNING

In this section,based on stochastic gradient descent(SGD)theory,we proposed an online optimization approach to solve task admission,user association,task offloading,and computing resource allocation in each slot.

3.1 SGD Based Temporal Decoupling

According to the necessary condition of rate stability[33],the queue stability of(8a)and(8b)can be equivalent to the following:

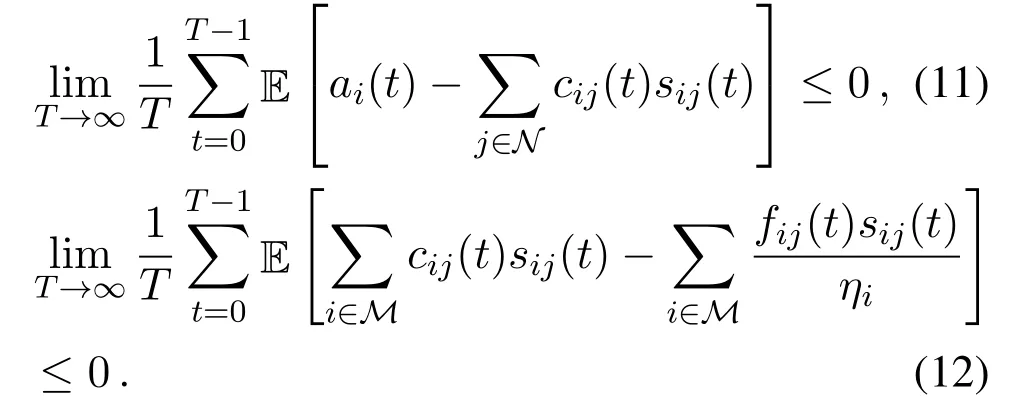
Then,the optimization problem(10)can be reformulated as:

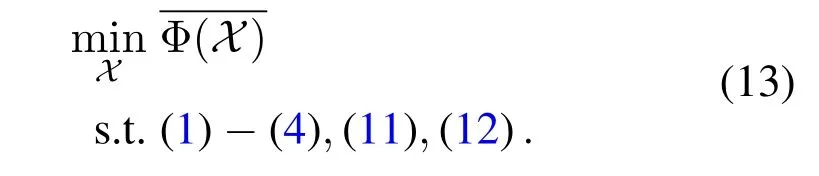
Leta(t)={ai(t),∀i∈M},s(t)={sij(t),∀i∈M,∀j∈N},c(t)={cij(t),∀i∈M,∀j∈N},andf(t)={fij(t),∀i∈M,∀j∈N}be the collection of task admission,user association,task offloading size and computing resource allocation at slott.By leveraging SGD theory[34],the optimization problem(13)can be transformed into a per-slot deterministic optimization problem,as given by

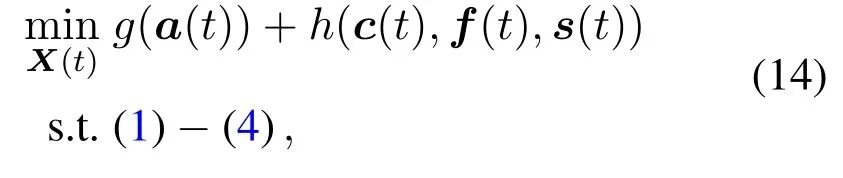
where

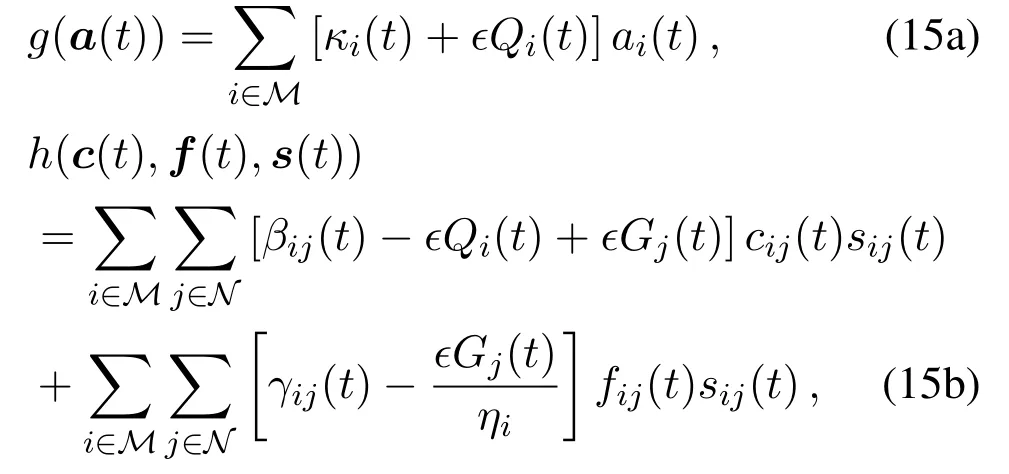
where∊is the step size.This reformulation is through SGD to update the Lagrange multipliers of(11)and(12)per slot.The detailed proof can refer to Appendix A.

3.2 The Per-slot Online Optimization

For the problem(14),the variables ofa(t)andc(t),f(t),s(t)can be decoupled in both objective function and constraints.That is,we have the following two optimization subproblems.

3.2.1 The Optimal Task Admission

The optimization problem of task admission can be given as

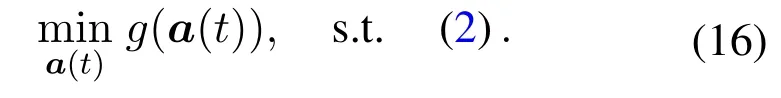
Since the above problem(16)can be decoupled among devices,it can be rewritten as

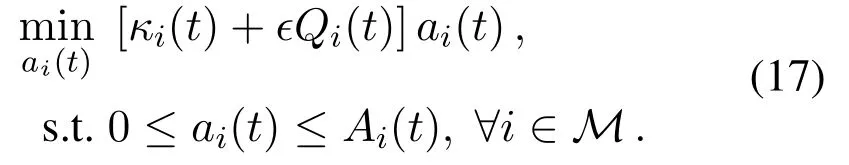
The optimal solution of(17)depends on the sign of parameterκi(t)+∊Qi(t),and can be given by

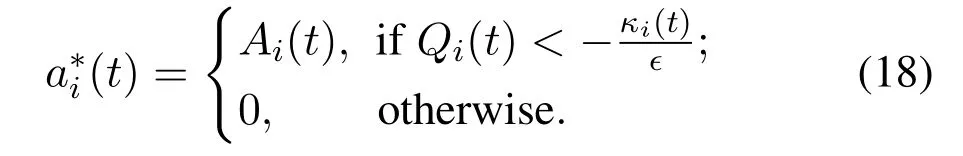
3.2.2 The Optimal User Association,Task Offloading,and Computing Resource Allocation

The joint optimization problem of user associations(t),task offloading sizec(t),and computing resource allocationf(t)can be written as

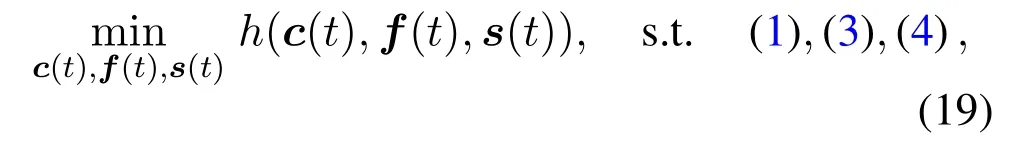
where the user associations(t)is a binary vector,and the task offloading size and computing resource allocation are continuous vectors,that is,the above problem(19)is MIP problem.By implementing alternative optimization technique,the MIP problem can be decomposed into two subproblems:i.e.,the optimization of task offloading size and computing resource allocation given user association,and the optimization of user association given the task offloading size and computing resource allocation.The detailed solutions are as follows:

The user association link can be written asK(t)={(i,j)|sij(t)=1}under the given user associations(t).Since the decisions of task offloading and computing resource allocation can be decoupled in the objective function and constraints of(19),the optimization of task offloading can be written as

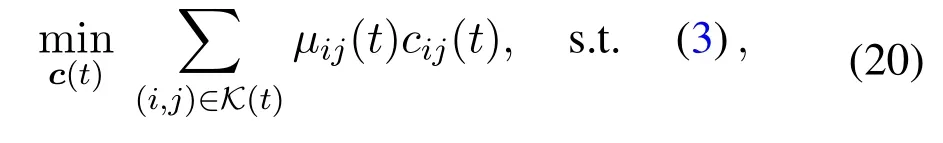
whereµij(t)=βij(t)−∊Qi(t)+∊Gj(t).The problem(20)is the linear programming of weighted-sum minimization[35],and the optimal solution of task offloading size can be obtained as

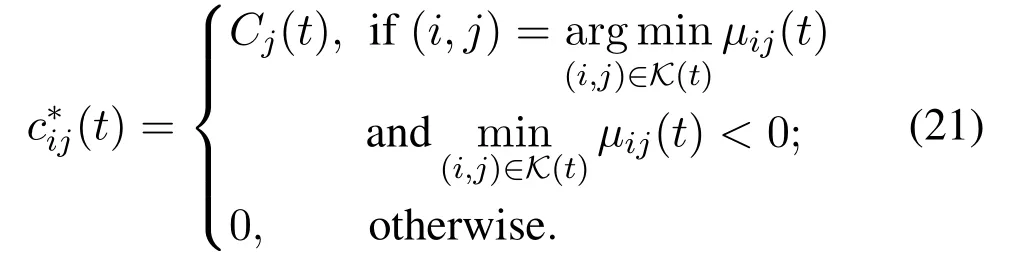
The optimization problem of computing resource allocation can be formulated as

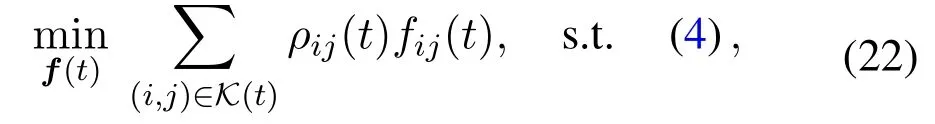
whereρij(t)=γij(t)−∊Gj(t)/ηi.The problem(22)is also the linear programming of weighted-sum minimization,the optimal computing resource allocation can be acquired by evaluating the parametersρij(t),as given by

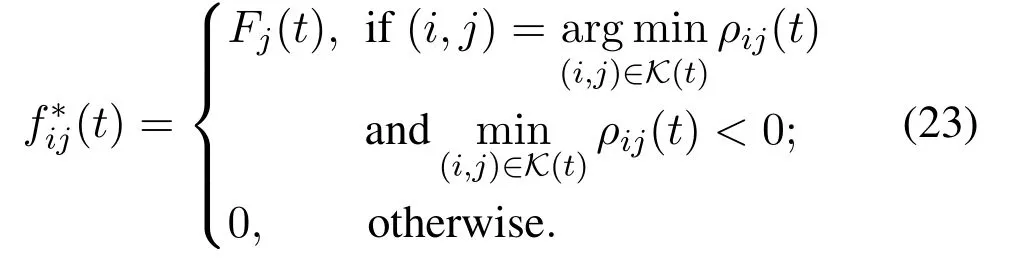
With the optimal solution of task offloading size and computing resource allocation in(21)and(23),the optimization problem of user association can be written as

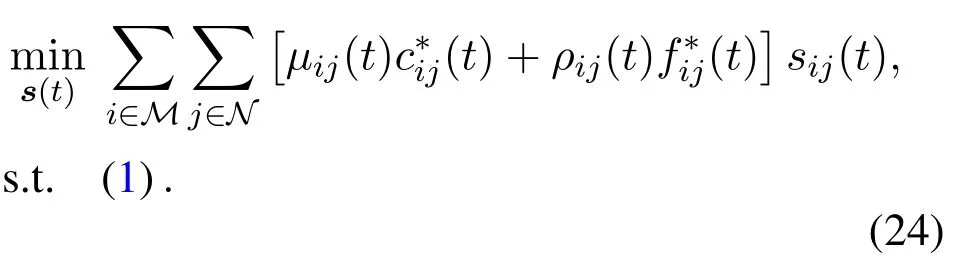
The above problem is integer programming(IP)problem due to the binary attribute of user associations(t).By expending the edge servers into the virtual server set with one connection capacity,N},where,the device setMand virtual edge server setN′can be interpreted as the two disjoint vertex sets in bipartite graph.The edge weight between deviceiand virtual serverpcan be given as

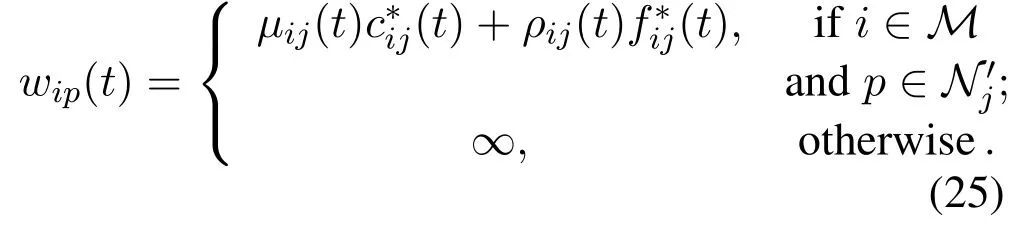
Then,the IP problem of user association becomes the minimum-cost maximum flow problem by adding the source vertexband sink vertexd,where the edge cost of unit flow is given by

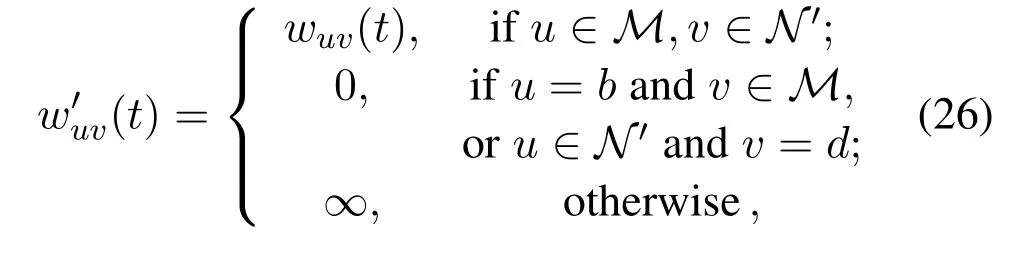
and the edge capacity(i.e.,the maximum allowable network flow on edge)is given by

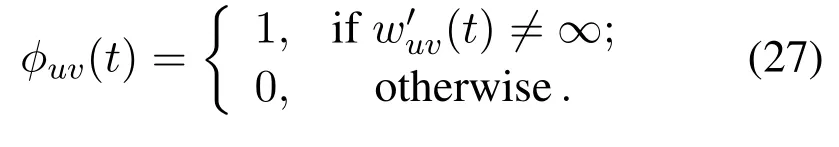
Algorithm 1.The per-slot online learning algorithm.At each slot t in device i:1:Acquire the queue backlog of Qi(t)and the operation cost parameter of κi(t);2:Implement the task admission a∗i(t)based on(18);At each slot t in edge servers:3:Acquire the queue backlogs of Qi(t)and Gj(t),and the operation cost parameters,including βij(t)and γij(t);4:Determine the task offloading size c∗ij(t)based on(21);5:Allocate the computing resource f∗ij(t)according to(23);6:Choose the user association s∗ij(t)by solving the minimum-cost maximum flow problem with edge cost(26)and edge capacity(27);7:Update Qi(t+1),Gj(t+1)according to(5)and(6),respectively.

The minimum-cost maximum flow problem can be optimally solved by using the Ford-Fulkerson algorithm(also known as the Edmonds-Karp algorithm[36]).Then,the optimal user associationif its corresponding edge has a positive flow assignment,otherwiseThen,the proposed per-slot online learning approach of user association and resource scheduling can be summarized in Algorithm 1.

3.3 Asymptotic Performance Analysis

Let Φoptbe the offline optimum with the a-prior knowledge of task arrivalAi(t),transmission capacityCj(t),and computing resourceFj(t)across all time slots.Let Φ∗be the optimum achieved by our proposed per-slot online learning algorithm.The performance of optimal user association and resource scheduling under Algorithm 1 can be derived in the following theorem.

Theorem 1.The optimality loss between the proposed per-slot online learning algorithm and the offline algorithm,i.e.,Φ∗andΦopt,satisfies the following:

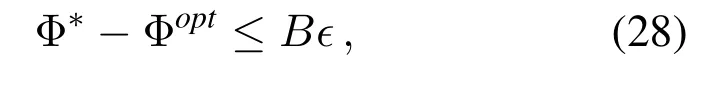
where B is the positive constant,as given by

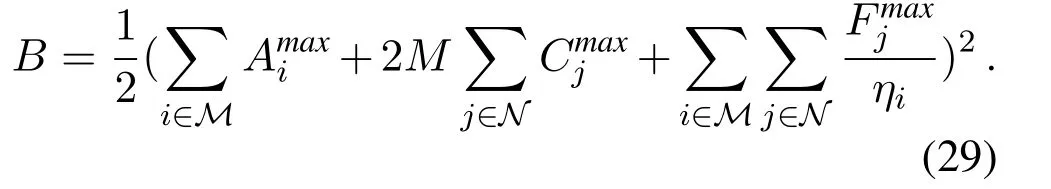
Proof.See Appendix B.

According to Theorem 1,the per-slot online learning algorithm can achieve asymptotic performance,that is,the optimality loss can be diminished as the step size of SGD∊→0.

IV.TWO-TIMESCALE ONLINE LEARNING

Since the changes in user association could trigger frequent handover and task migration,and cause high network overhead in terms of delay and energy consumption,we extend the per-slot online learning approach in Section III to a two-timescale online learning of user association and resource scheduling.

4.1 Algorithm Description

As shown in Figure 2,Wis the time interval in terms of the number of time slots between two consecutive decisions of user association.The proposed optimization framework operates with two timescales,where the user association is implemented on a larger timescale(i.e.,perWslots),and the task admission,task offloading size and computing resource allocation are determined on the small timescale(i.e.,per single slot).

Letw(t)={Ai(t),Cj(t),Fj(t),∀i∈M,∀j∈N}be the collection of random process of task arrival,transmission capacity and computing resource across all devices and edge servers at slott.Θ(t)={Qi(t),Gj(t),∀i∈M,∀j∈N}is the vector to collect all the queues of device and edge servers.For the large time-scale optimization of user association,at slott=kW,the user association is decided by minimizing the expectation of the sum of(24)across slotst∈T ′={kW,kW+1,··· ,(k+1)W −1},as given by

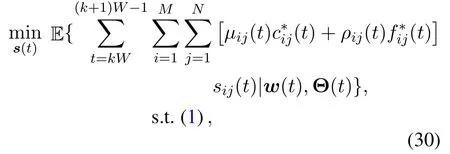
wheresij(kW)=sij(t),∀t∈T ′,which means once the user association decision is made at slott=kW,it remains unchanged in the subsequentW −1 slots.

At the(kW)-th time slot,the exact calculation of expectation in(30)requires the entire accurate knowledge of random processesw(t)and queue vector Θ(t)acrosst∈T ′,which is not feasible because the observable queue backlogs are onlyQi(kW)andGj(kW).Based on the theory of mini-batch learning,the queue backlogs can be approximated byQi(kW),and∀t∈T ′[37].The batch size of SGD is equal to the number of slots in the large timescale(i.e.,W).With online gradient being updated once everyWslots,the variance of SGD can be reduced[37,38].Similarly,the operation cost parameters can be approximated asandWith these approximations,we have

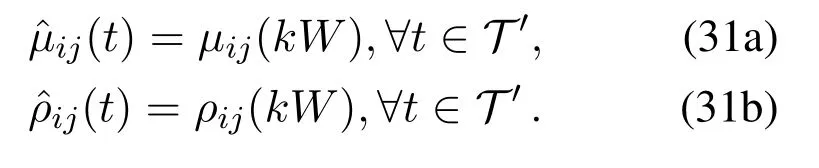
Then,the user association on the large timescale can be reduced to solve the problem(24)at slott=kW,that is,to obtain the optimal user associationby solving the minimum-cost maximum flow with edge cost(26)and edge capacity(27).The user association keeps unchangedduring the large time-scale intervalst∈T ′.Under the user associationobtained by the large time-scale optimization,the decisions of task admission,task offloading size and computing resource allocation can be optimized on the small timescale with per-slot optimization.

For the optimization of task admission,task offloading and computing resource allocation on the small timescale,the random processesw(t)and queue vector Θ(t)are observed in each slott,and the decisions are made per slot.The task admission,task offloading size and computing resource allocation are optimized based on(18),(21)and(23),respectively.After the small-timescale decisions,the queue vectors are updated according to(5)and(6).The proposed twotimescale online learning algorithm is described in Algorithm 2.

Algorithm 2.The two-timescale online learning algorithm.At each slot t=kW,k∈N:▷On the large timescale 1:Acquire the random processes w(kW)and queue vector Θ(kW);2:Approximate the queue backlogs and operation cost parameters to calculate(31a)and(31b);3:Choose the user association s∗ij(kW)by solving(30)based on(26)and(27);At each slot t∈{kW,kW +1,··· ,(k+1)W −1}:▷On the small timescale 4:Remain the unchanged user association s∗ij(kW)across slots t;5:Optimize the task admission a∗i(t)based on(18);6:Obtain the task offloading size c∗ij(t)based on(21);7:Decide the computing resource f∗ij(t)according to(23);8:Update Qi(t+1),Gj(t+1)according to(5)and(6),respectively.

4.2 Asymptotic Performance Analysis

The performance of two-timescale online learning algorithm satisfies the following theorem.

Theorem 2.The optimality loss between the average cost achieved by the proposed two-timescale online learning algorithmand that in the offline algorithmΦopt,is given by

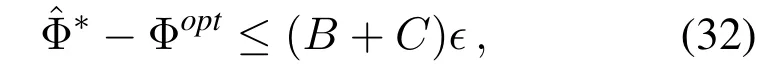
where B is defined in(29),and C is finite constant as

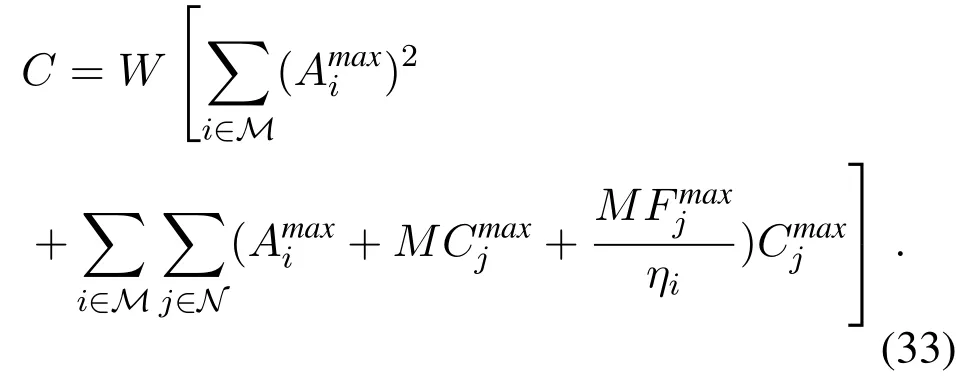
Proof.See Appendix C.

Theorem 2 indicates that the optimality loss can asymptotically diminish with the step size∊.The upper bound of optimality loss increases with the slot interval in the large timescale,i.e.,W.The proposed two-timescale online learning algorithm can preserve the asymptotical optimality while reducing the network overhead caused by frequent user associations.

4.3 Time-complexity Analysis

LetEi(t)denote the set of admissible edge servers of deviceiat slott(i.e.,Ei(t)={j|eij(t)=1}).The proposed two-timescale online learning algorithm consists of two parts:the resource management decisions are made on a small timescale,and the user association operations are performed on a large timescale.For the small timescale decision,the time-complexity depends on the parameter evaluation in task admission,task offloading and computing resource allocation according to(18),(21),and(23),respectively.Therefore,the overall time-complexity of small timescale decision-making isO(M+M|Ei(t)|+M|Ei(t)|)=O(M|Ei(t)|)≤O(MN).For the large timescale,the user association is performed by solving the minimum-cost maximum flow problem of(26)and(27)in perWslots.The time-complexity of large timescale optimization is dominated by the Ford-Fulkerson algorithm asO(|V|×|E(t)|2),where|V|and|E(t)|are the number of vertexes and edges in the directed graph of flow network constructed by(26)and(27).

V.PERFORMANCE EVALUATION

To evaluate the performance of the proposed algorithms,we simulate a MEC network consisting ofM=20 IoT devices andN=4 edge servers overT=50000 slots.For each serverj∈N={1,2,3,4},the connection capacitySj∈[2,8]is an arithmetic sequence withS1=2 andSj=Sj−1+2.The common computing intensity of each device isηi=238 CPU cycles/bit,∀i∈M[39].At slott,the random network environment in terms of task arrived(Kbit)at each device,the transmission capacity(Kbit),and the computing resource(GHz)of each edge server are given below.

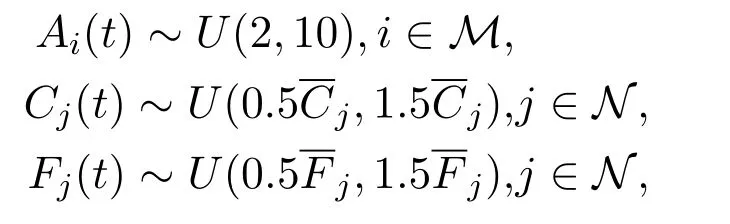
whereU(a,b)is the uniform distribution withaandbbeing the lower and upper bounds,respectively.The above upper bounds represent the maximum valueandis the mean value of transmission capacity of each serverj∈N.This mean value is an arithmetic sequence[40].In particular,andSimilarly,is the mean value of computing resource capacity for edge serverj∈N,and this arithmetic sequence has a pattern ofand

The common per unit operation cost of task admission for each device isκi(t)～U(−2,0)per Kbit,the negative probability distribution is to excite the data admission to devices[41].The common perunit operation costs of task offloading and computing processing areβij(t)～U(0.2,1)per Kbit andγij(t)～U(1,10)per GHz,respectively.

The time-averaged operation cost of the proposed online learning algorithms will be compared with two baseline schemes:1)theequal allocation policythat evenly divides the transmission capacity and computing resources among the connected devices; 2)thepriority-based policy,which allocates the maximal transmission capacity and computing resource of edge server to the device with the highest priority in terms of the largest queue backlog[42].

5.1 The Impact of Step Size

In Figure 3,as the reciprocal of step size increases,1/∊∈[45,210],the time-averaged operation cost of the proposed per-slot online learning decreases and stabilizes with 1/∊≥120(i.e.,∊≤0.0083).That is,the per-slot online learning algorithm can obtain asymptotically optimal performance as the step size∊decreases(i.e.,the optimality loss can be asymptotically diminished),as shown in Theorem 1.

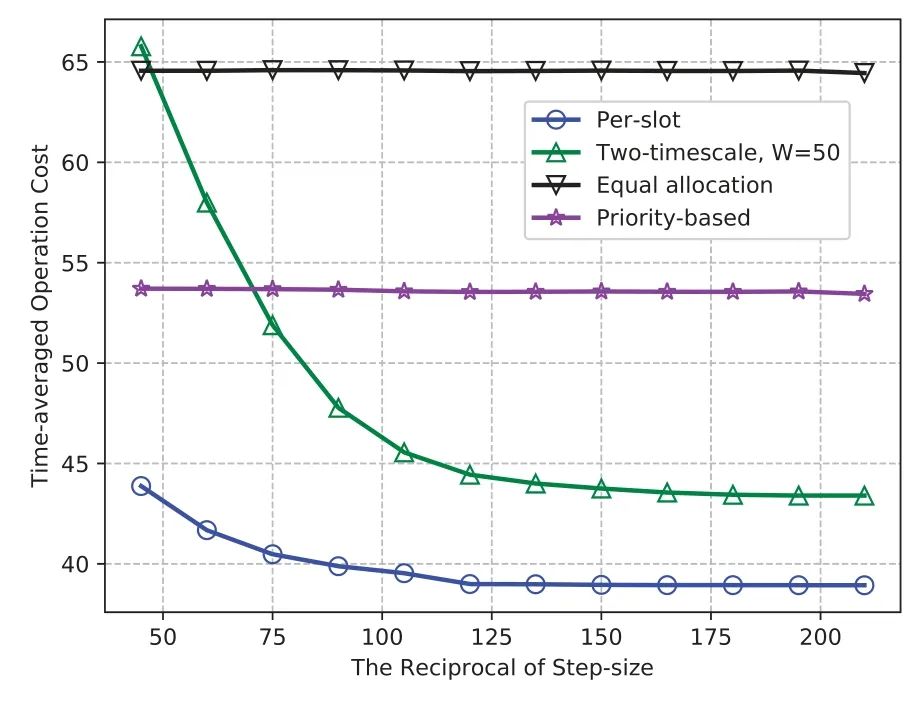
Figure 3.The operation cost v.s. 1/∊.

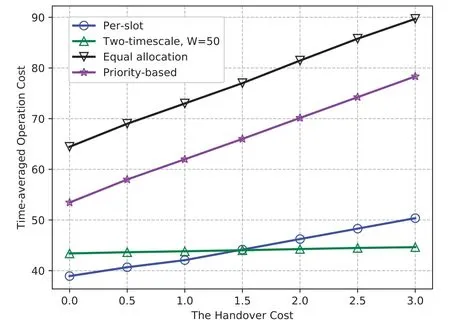
Figure 4.The operation cost v.s.the handover cost,(with 1/∊=210 ≥180 to ensure the convergence of the algorithms).

The proposed two-timescale online learning algorithm with the large timescale interval ofW=50 can achieve stable operation cost with 1/∊≥180(i.e.,∊≤0.0056),and its stabilized operation cost is higher than the per-slot learning algorithm.This is because the user association is updated once everyWtime slots with the two-timescale learning algorithm,and the approximated queue backlog and environment randomness result in the increased optimality loss.The asymptotic optimal performance and the increased optimality loss of the proposed two-timescale algorithm are consistent with Theorem 2.

The time-averaged operation costs of the two baseline schemes remain unchanged regardless of the step size.The proposed approaches are superior to these two comparison schemes because of the joint optimization of user association and resource scheduling which captures the environment randomness.In addition,the priority-based allocation method can obtain lower operation cost than the equal allocation policy,by allocating the maximal transmission capacity and computing resource of edge server to the highest priority device with the largest queue backlog.However,the equal allocation policy evenly allocates the transmission capacity and computing resources to the connected devices.The mismatches between task admission and resource scheduling will lead to a higher cost.

5.2 The Impact of Network Overhead

We introduce the handover/re-association cost to quantify the total overhead of network handover and task migration,which is added to the network operation cost when the user association between different time slots changes.In Figure 4,with the per-handover cost ranging from 0 to 3,the average operation cost of the proposed two-timescale online learning algorithm increases slightly with the handover cost.The increase rate of the two-timescale learning approach is lower than the per-slot online learning algorithm,and they have the same operation cost when the handover cost is 1.5.This is because the two-timescale method updates the user association perWslots,which can reduce the number of network handover/migration compared to the per-slot learning.The other two benchmark schemes have much higher operation costs because users are randomly mapped to the edge server at each slot.The resulting large number of network handover/migration causes operation cost increasing rapidly and linearly with the handover cost.As a result,the two-timescale online learning method is more effective in a complex network environment with high handover cost,and the per-slot optimization has better performance under low handover cost.

5.3 The Impact of Task Arrival

In Figure 5,the time-averaged operation costs of our proposed algorithms and the other two benchmarks all increase with the task arrival(i.e.,the maximal task arrival).The operation costs of equal allocation policy and priority-based allocation policy grow faster since they admit all arrived task into the queue at each slot.The heavier consumption of communications and computing resources will lead to high operation costs and a faster growth rate.The prioritybased scheme has relatively slower growth because the edge server allocates resources to its associated device with the longest queue.The proposed online learning approaches have less operation cost because the computing task is admitted to the device according to(18),and the two-timescale learning algorithm has a higher cost because of the optimality loss caused by the approximated backlogs and parameters on the large timescale.

5.4 The Impact of Connection Capacity

Figure 6 shows the changes in the operation cost with different connection capacities(i.e.,SNis the maximal connection capacity of all edge servers becauseSj∈[2,SN]is an arithmetic sequence withS1=2).As the connection capacity increases,the time-averaged operate cost of all schemes first rises and then stabilizes.As the connection capacity of edge server increases,the number of devices that can be served in each time slot increases.This leads to the linear increase of computing tasks admitted to the network,and a gradual increase in operation cost.The time-averaged operation cost remains unchanged when the connection capacity of edge servers is greater than the number of devices in edge network(i.e.,8).This is because with limited number of devices,further increment of connection capacity will no longer improve the admission of computing tasks,hence,no more operation cost.The equal allocation policy has a higher growth rate and operation cost than the priority-based scheme,the reason is that the increase in connection capacity leads to the same increase in devices to participate in task offloading and resource allocation.

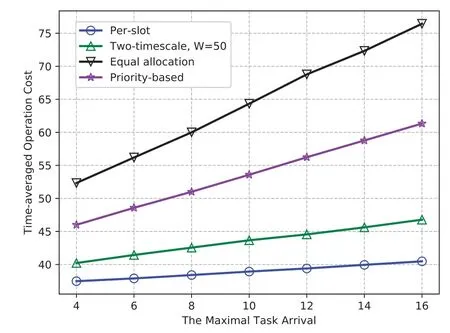
Figure 5.The operation cost v.s.,(with 1/∊=210).

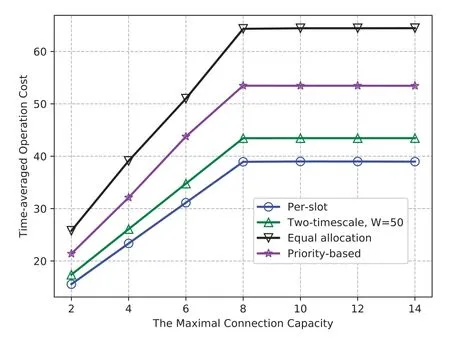
Figure 6.The operation cost v.s.SN ,(with 1/∊=210).

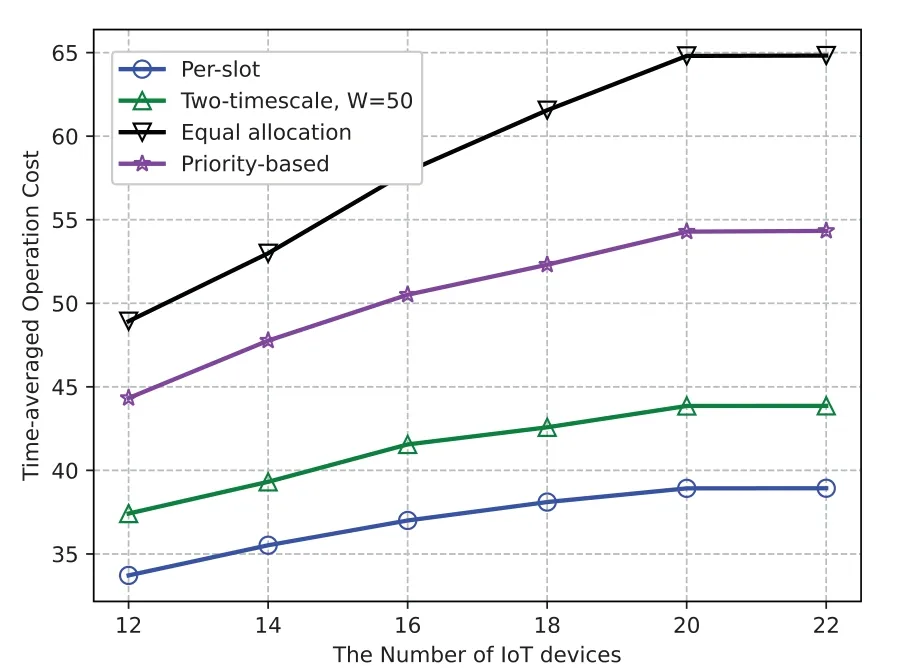
Figure 7.The operation cost v.s.M,(with 1/∊=210).

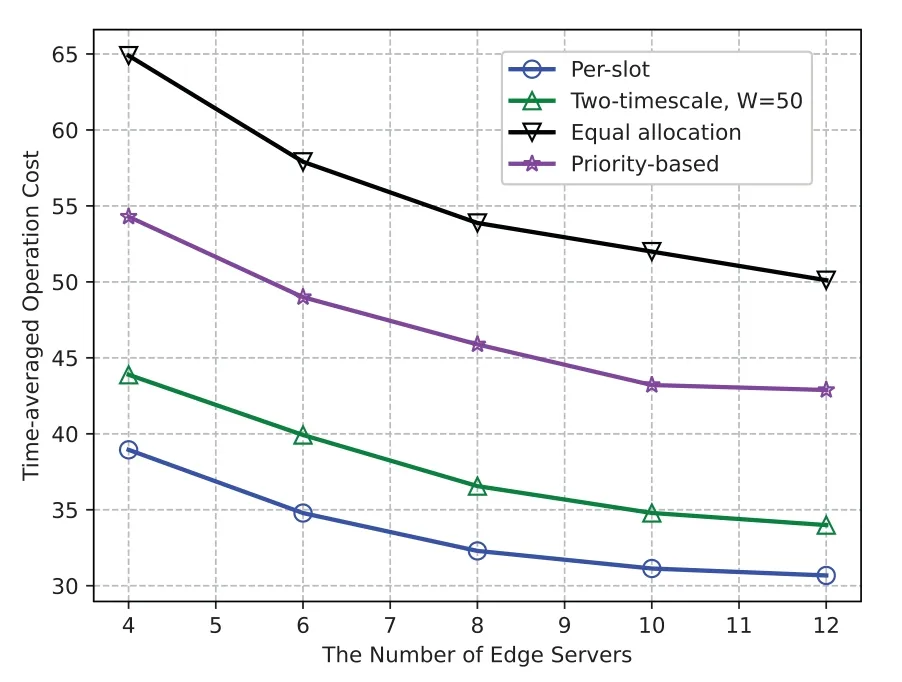
Figure 8.The operation cost v.s.N,(with 1/∊=210).

5.5 The Impact of Number of Devices and Servers

As illustrated in Figure 7,when the number of IoT devices(i.e.,M)increases,the time-averaged operation cost will increase first and then tend to remain unchanged.With small number of IoT devices(M ≤20),the operation cost gradually increases with less and less momentum.This is because the computing task admitted into edge network will increase withM,and as shown in(18),(21),and(23),the operation cost consumed to perform task offloading and computing processing will increase.However,the limited wireless resource and computing resource limits the growth speed of operation cost,i.e,the growth of the server task queue can inhibit the task offloading from the devices and slow down increment of the operation cost.When the number of devices in the network exceeds the total connection capacity of edge servers(M >20),the operation cost will stay as a constant.

In Figure 8,we evaluate the impact of the number of servers deployed in the edge network on the timeaveraged operation cost.When the number of servers(i.e.,N)increases,the time-averaged operation cost gradually decreases and tends to level off.WithN=12,as compared with the equal allocation policy,the proposed per-slot online learning algorithm and twotimescale online learning algorithm can reduce the operation cost by 38.78% and 32.17%,respectively.This verifies the superiority of the proposed algorithms compared to the benchmark schemes.As the number of edge servers increases,the time-averaged operation cost will decrease,because there is a higher probability that each device can associate with an edge server with a lower operation cost per unit(i.e.,κi(t),βij(t)andγij(t))in dynamic edge computing network.Owing to the limited number of devices and the bounded nature of randomness(i.e.,Ai(t),Cj(t)andFj(t)),the operation cost will stabilize.

VI.CONCLUSION

In this paper,we first proposed the per-slot online learning approach to jointly optimize the user association and resource scheduling,aiming at minimizing the time-averaged operation cost in MEC network consisting of multiple base stations and multiple devices.By leveraging the theories of stochastic gradient descent and minimum cost maximum flow,the asymptotic optimality can be achieved without requiring a-prior knowledge of task arrival,transmission capacity,and computing resource availability.To alleviate the high network overhead caused by frequent user associations,the two-timescale online learning approach was developed to perform user association on the large timescale and resource scheduling on the small timescale.According to theoretical analysis,this two-timescale optimization method can still preserve the asymptotically optimal cost.Simulation results demonstrated the effectiveness and superiority of our proposed algorithms.

ACKNOWLEDGEMENT

The work was supported by the National Natural Science Foundation of China(61971066,61941114)and the Beijing Natural Science Foundation(No.L182038),National Youth Top-notch Talent Support Program.

APPENDIX A

Recall thatw(t)is the independent and identically distributed(i.i.d.)random processes between time slots.The time average of(11)and(12)can be rewritten as

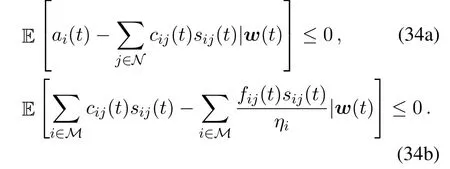
Then the problem(13)can be reformulated as

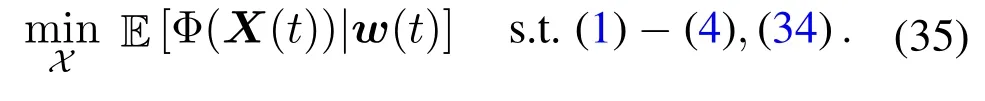
Letλ={λi,∀i∈M}andζ={ζj,∀j∈N}be the Lagrange multipliers of(34a)and(34b),respectively.The Lagrangian of(35)is given by

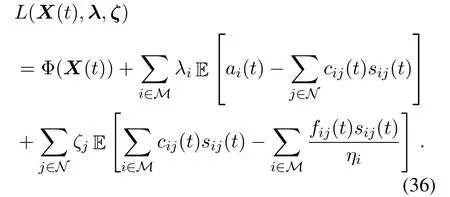
The dual problem of(35)is written as

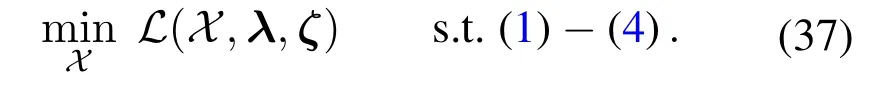
By using SGD technique,instead of accurate gradient,we can update the Lagrangian multipliers as follows

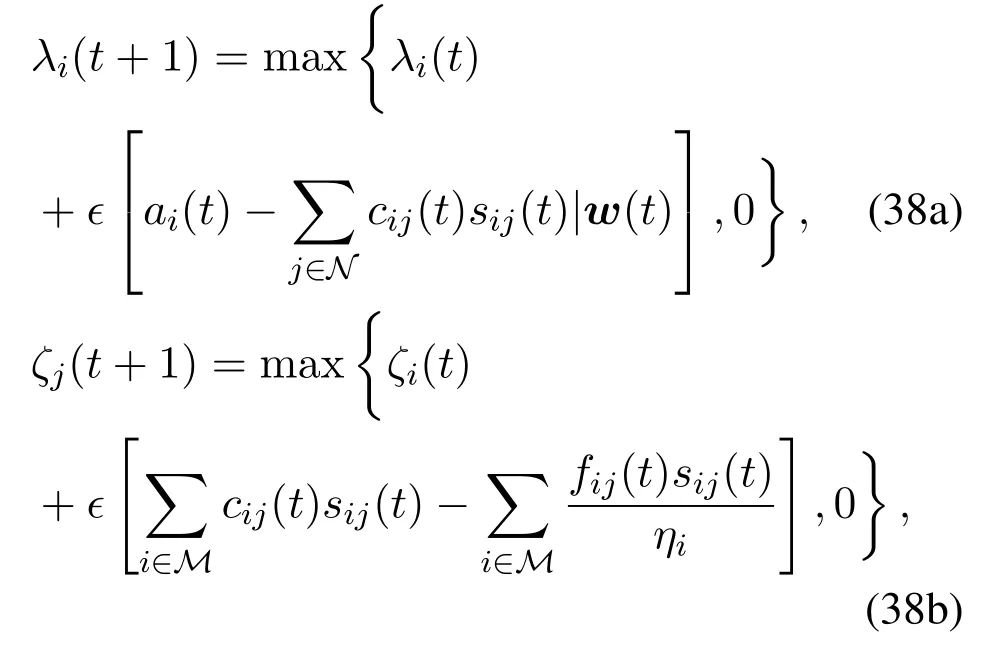
where∊is the step size of SGD.By comparing(34)with(5)and(6),it can be founded that the multiplier updates are linear related to the queue updates,we haveλi(t)=∊Qi(t)andζj(t)=∊Gj(t).Substitutingλi(t)andζi(t)into(37),we can have(14).

APPENDIX B

Taking squares of both sides of(5)and(6),we have

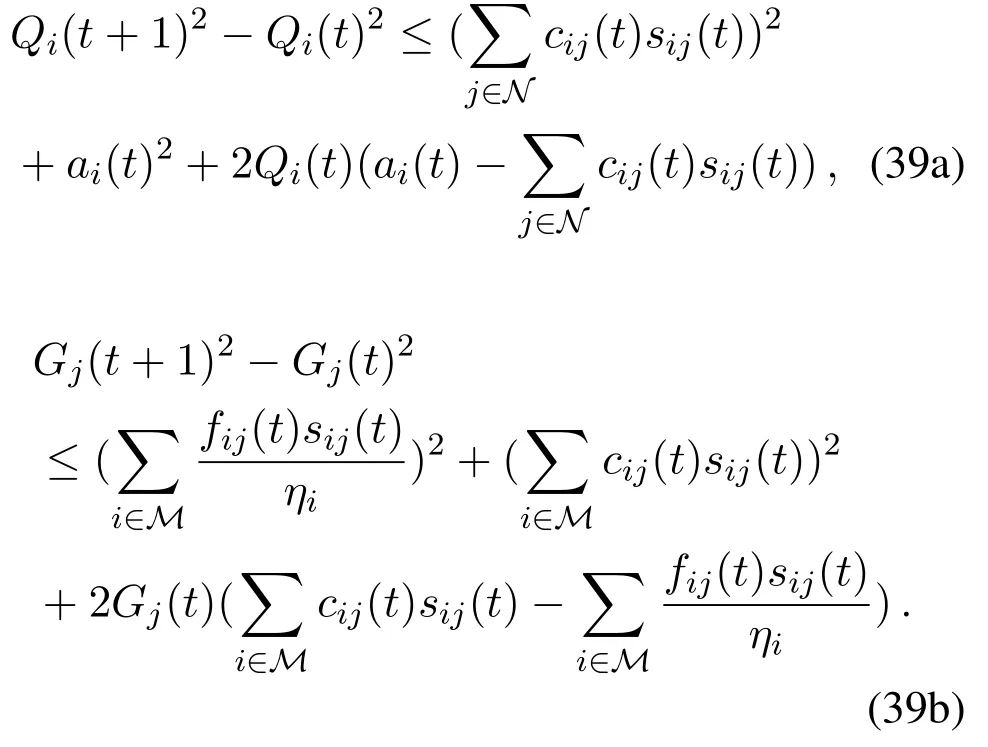
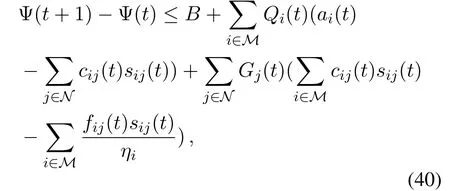
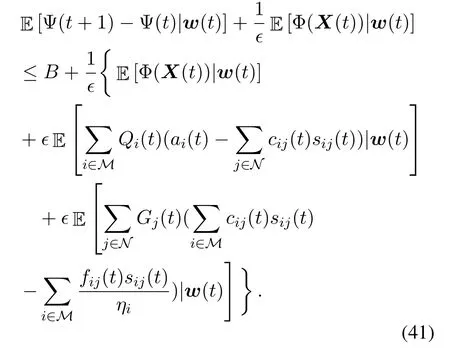
By substituting(41)with(36),we have

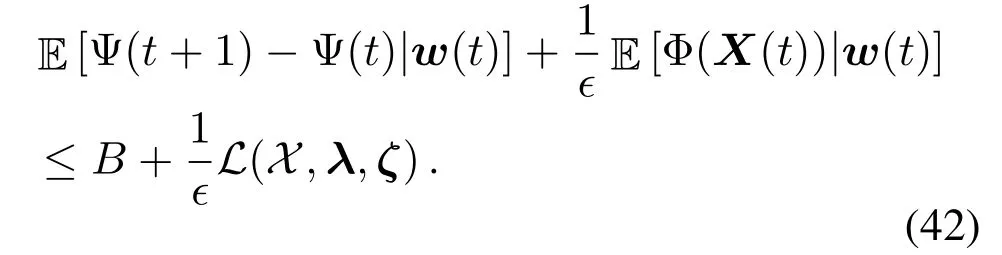
Summing up the inequalities of(42)overTslots,then dividing byTand takingT →∞,we have

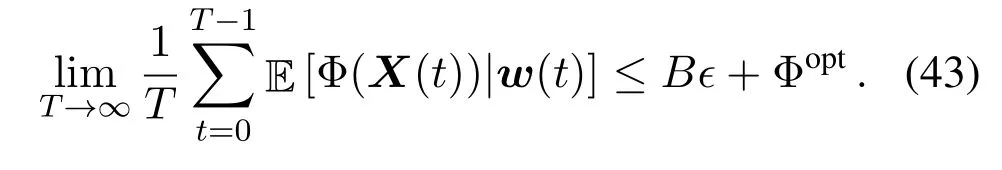
By replacing the left-hand-side of(43)with Φ∗,the result of(28)can be obtained.

APPENDIX C

According to the approximation of queue backlogs,we haveτ∈{0,1,··· ,W −1}.We have

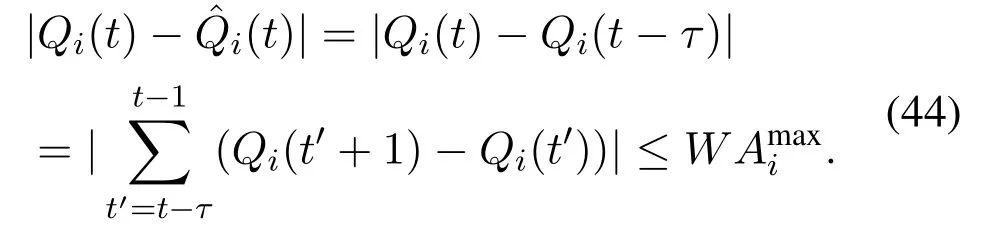
Similarly,we have

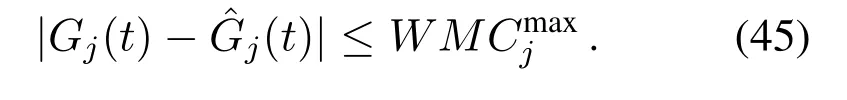
Letξi(t)=κi(t)+∊Qi(t)be the weighted parameter in(15a),the difference between the approximate parameterand the actual parameterξi(t)is:

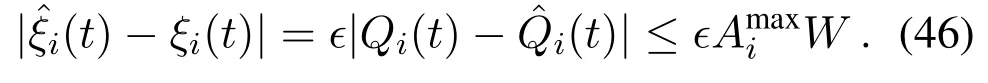
Similarly,we have

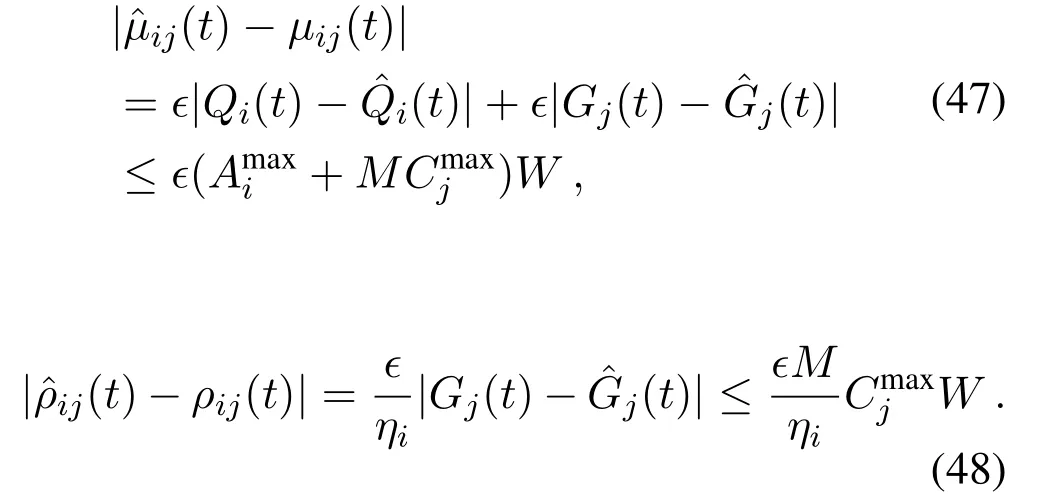
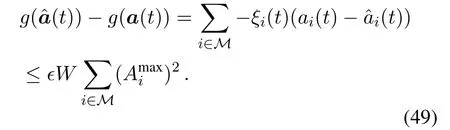
Similarly,we have

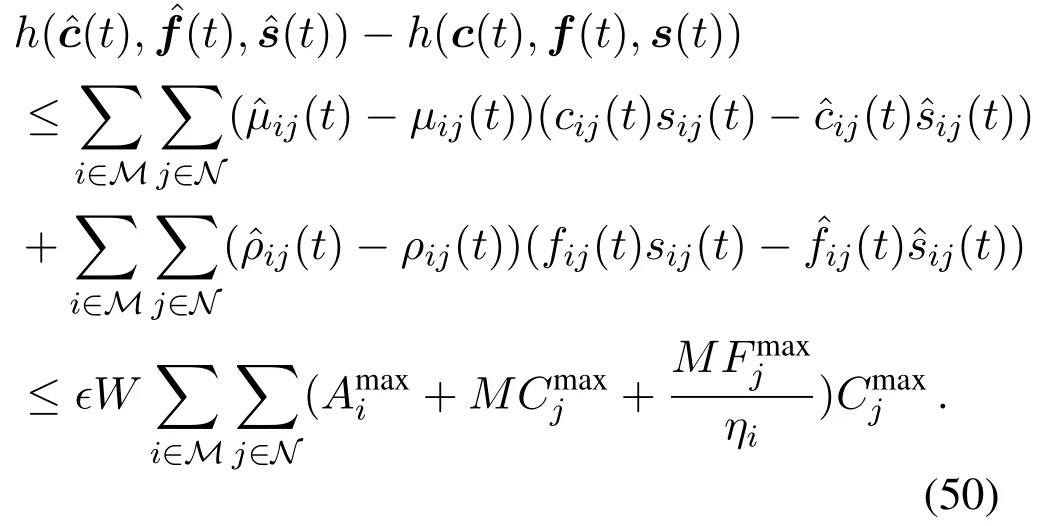
By summing up the inequalities of(49)and(50)overt=0,1,··· ,T −1,then dividing byTand takingT →∞,we can obtained the result of(32).