A Log-Penalty-Based Method for Multi-Parameters Estimation with Partly Calibrated COLD Array
Yudi Qin,Xiaoying Sun
College of Communication Engineering,Jilin University,130012 Changchun,China
Abstract:In this paper,we focus on the problem of joint estimation of DOA,power and polarization angle from sparse reconstruction perspective with array gain-phase errors,where a partly calibrated cocentered orthogonal loop and dipole(COLD)array is utilized.In detailed implementations,we first combine the output of loop and dipole in second-order statistics domain to receive the source signals completely,and then we use continuous multiplication operator to achieve gain-phase errors calibration.After compensating the gain-phase errors,we construct a log-penalty-based optimization problem to approximate ℓ0 norm and further exploit difference of convex(DC)functions decomposition to achieve DOA.With the aid of the estimated DOAs,the power and polarization angle estimation are obtained by the least squares(LS)method.By conducting numerical simulations,we show the effectiveness and superiorities of the proposed method.
Keywords:multi-parameters estimation; log penalty;DC functions decomposition;partly calibrated COLD array;gain-phase errors
I.INTRODUCTION
Direction of arrival(DOA)estimation using antenna arrays plays an important role in many engineering fields,including radar,sonar,mobile communication and Internet of Vehicles(IoV),etc[1].So far,there have been a lot of works for DOA estimation,but most of them are proposed based on scalar antenna arrays,where the polarization information embedded in electromagnetic(EM)sources cannot be exploited.
In recent years,as the EM-vector sensor become more and more reliable,the problem of DOA and polarization estimation using EM-vector sensor arrays has attracted increasing research,and many suited methods with different kinds of EM-vector array have been presented,examples including the uni-vectorsensor ESPRIT method[2]using a single electromagnetic vector sensor;the MUSIC[3],the One-Bit MUSIC(OBMUSIC)[4]and theℓ1-norm minimization[5]based methods using cross-dipole(CD)arrays or sparse CD arrays; the MODE method[6],the SPSESPRIT method[7],theℓ1-PSRCM method[8]and the rank reduction(RARE)method[9]using a cocentered orthogonal loop and dipole(COLD)array.Theoretical analysis and numerical simulations have shown that the above mentioned methods have satisfied performance.However,it should be noted that the performance of these methods is critically rely on the knowledge of the array manifold.In practice,there always exists various array model errors(such as gain-phase errors,mutual coupling and positions uncertainties)[10–12],which could result in a serious performance degradation of the corresponding estimators.Recently,Maet al.,[13]proposed a subspace based technique for mixed source localization using a linear tripole array with gain-phase errors,where fourth-order cumulant is utilized.By applying a linear dipole array,Roccaet al.,[14]proposed a single snapshot based method for DOA estimation with mutual coupling.Instead of using subspace technique,the Bayesian approach combined with an iterative multiresolution strategy is adopted.
In this paper,we also take the influence of array gain-phase errors into account and further propose a new method for joint DOA,power and polarization angle estimation with a partly calibrated linear COLD array.This method will be a good supplement of existing polarized parameter estimation theory with array uncertainties.Through making full use of COLD array output as well as jointly using continuous multiplication operator(CMO)[15],log penalty and DC decomposition[16],the proposed method can provide an improved multi-parameters estimation performance,which has been efficiently validated by numerical simulations.
Notations:Throughout this paper,the upper-case(lower-case)boldface letters denote matrices(vectors),the superscripts∗,T,Hand†are the conjugate,transpose,conjugate transpose and pseudo-inverse,respectively.IMstands for theM ×Midentity matrix.‖·‖pdenotes theℓp-norm,wherep=0,1,2.vec(·),∠[·]and diag{·}represent the statistical expectation,vectorization,the phase of a complex number and diagonalization operation,while⊗and⊙are Kronecker product and Schur-Hadamard,respectively.
II.PROBLEM FORMULATION
Consider a uniform linear array(ULA)composed ofMCOLD elements receivingKnarrowband completely polarized signals,as depicted in Figure 1.The impinging signals are located atx−yplane with DOAsθk∈(−90◦,90◦),wherek=1,2,...,K.According to the electromagnetic field theory,it can be easily obtained that the electric-field vectorand the magnetic-field vectorof an incoming signal can be expressed as
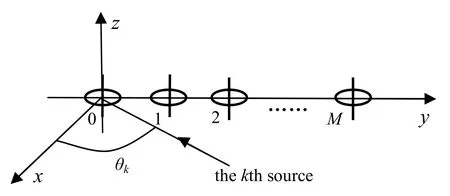
Figure 1.Adopted uniform linear COLD array structure.

where the polarization angleγand the polarization phase differenceηare used to characterize the polarization state,which satisfyγ∈[0,π/2)andη∈[−π,π),respectively.Let the 0th element as the phase reference point and further take the unknown and direction-independent gain-phase errors into account,the data outputs at sensormfor loop and dipole,denoted byandcan be given by
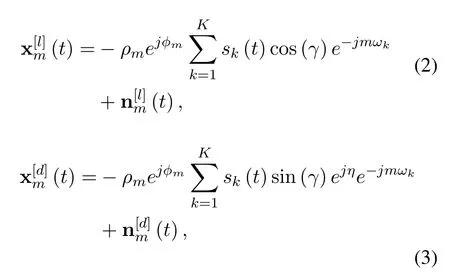
which directly yield the result that the observed data vectorsat time instanttcan be expressed as
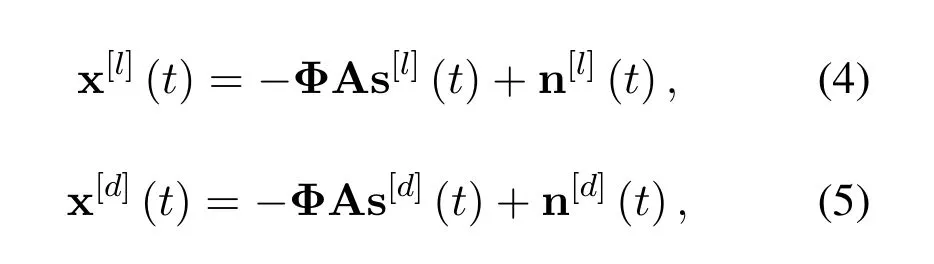
where

ωk=2πdsin(θk)/λwithdandλdenoting the interelement spacing and carrier wavelength,respectively.ρmandφmdenote the gain error and phase error of themth sensor,respectively.
In this paper,the following assumptions are required to hold:
•The noise terms n[l](t)and n[d](t)are stationary,zero-mean and spatially white Gaussian with same noise variance.
•The impinging signalssk(t),k=1,...,K,are independent each other and also independent of the noise.
•The gain-phase errors for loop and dipole at the same sensor are identical.The firstMcCOLD sensors have been calibrated,i.e.,whereMcdenotes the number of well calibrated COLD sensors and satisfiesMc ≥2.
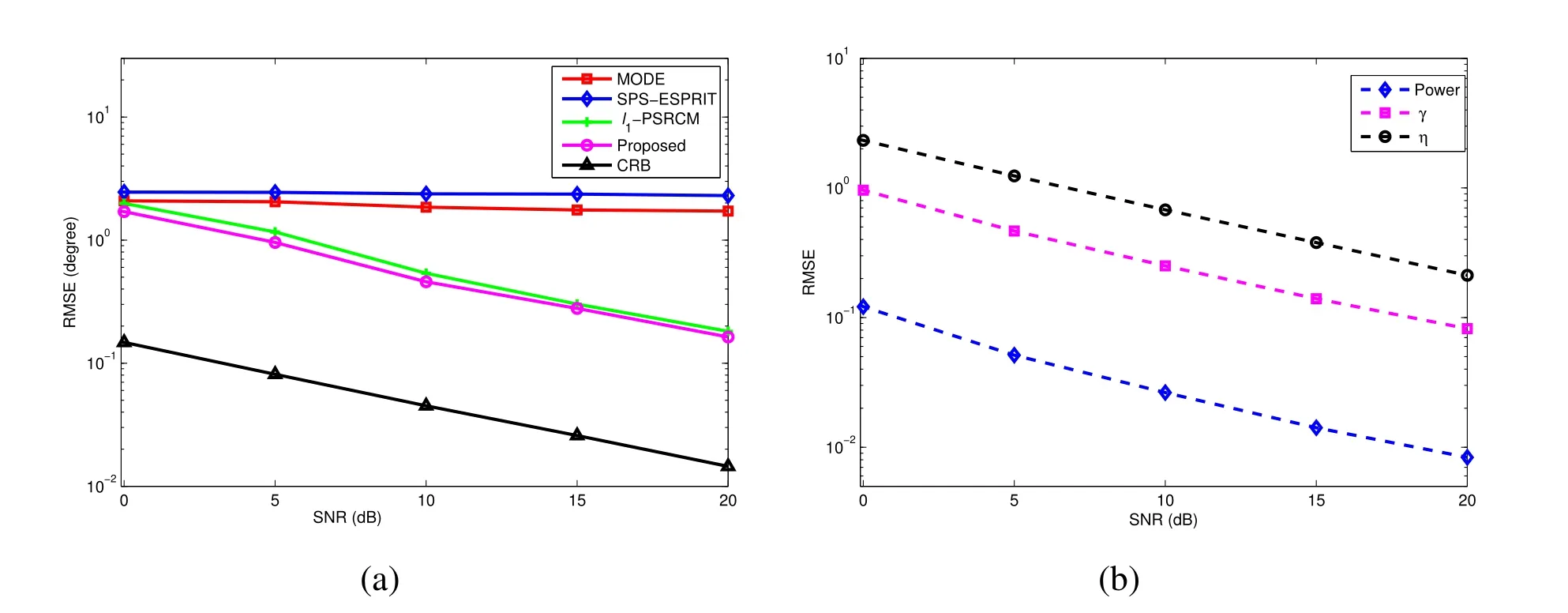
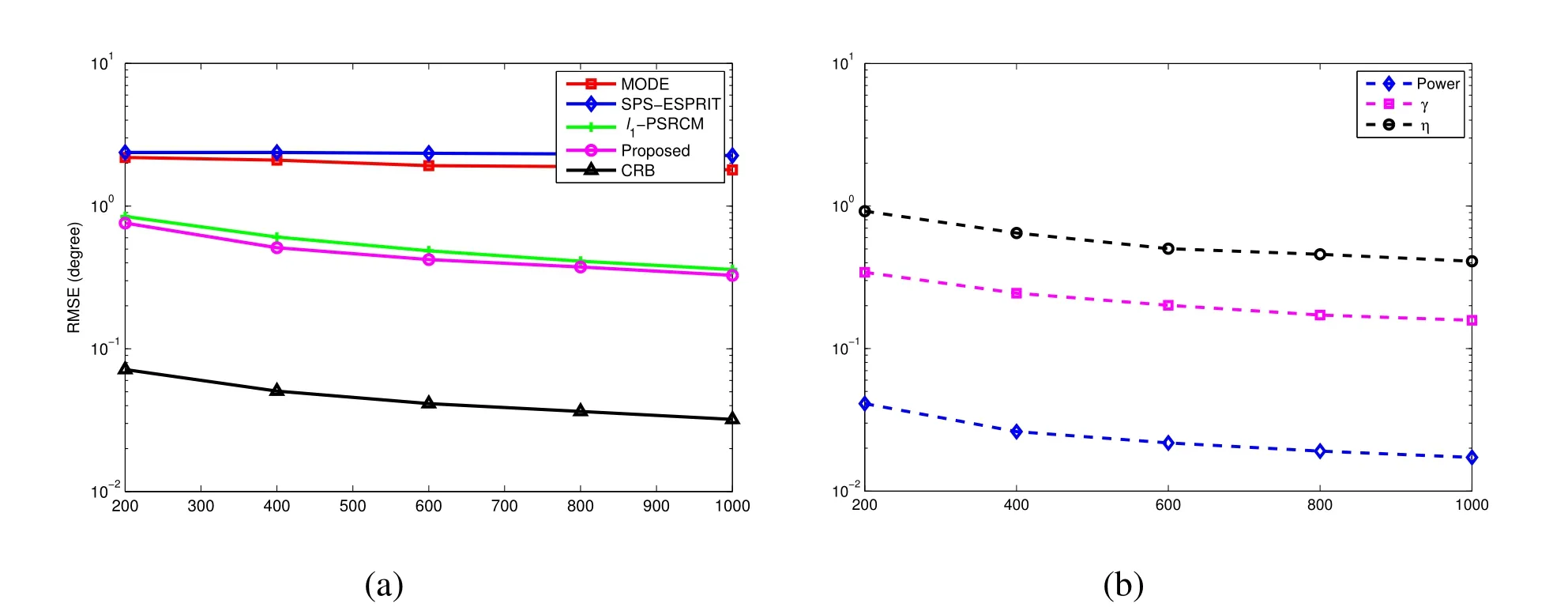
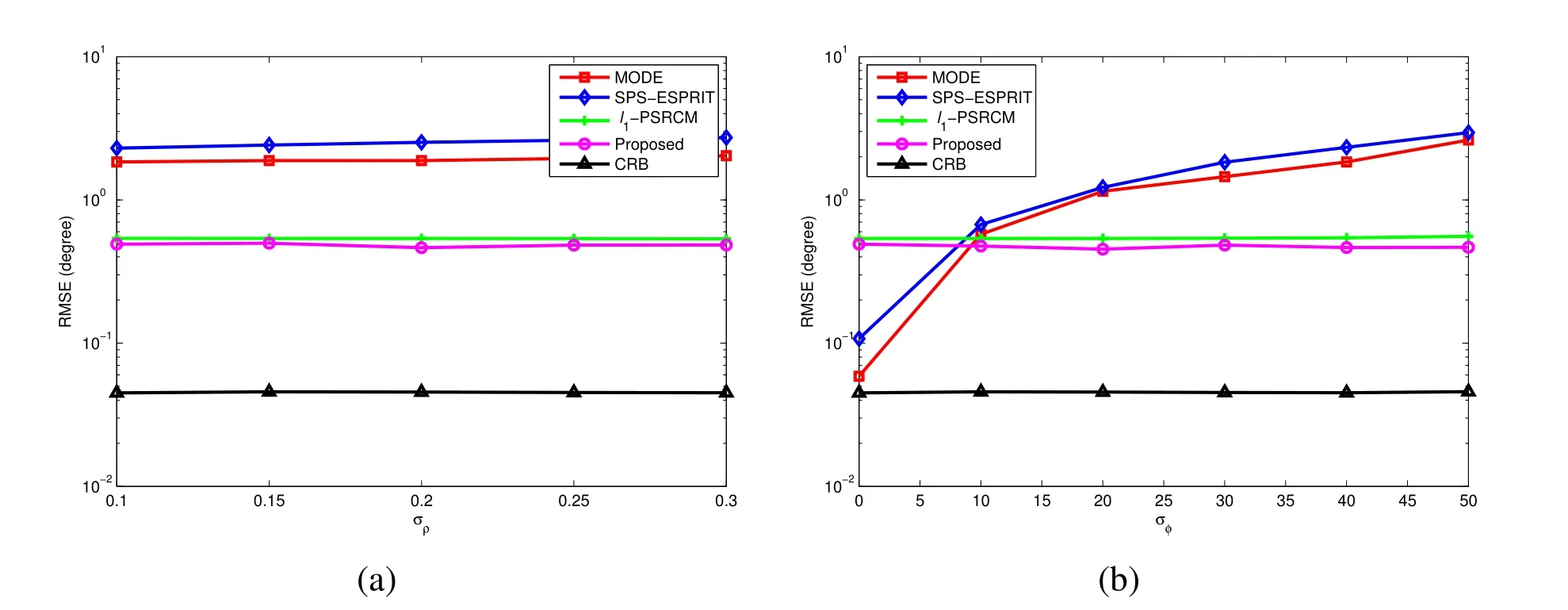
•The number of sensors and the inter-element spacing of the array satisfyK Remark 1.The fundamental premise of assumption 3 is that the amplifier and the clock corresponding to the mth loop and dipole are same,which leads to the identical gain-phase errors.In fact,this condition is consistent with the actual antenna array reception.Moreover,it should be pointed out that even if their gainphase errors are different,the proposed method can also calibrate them,see the next section for details. Based on(4)and(5),we obtain the auto-polarized covariance matrices as Combining Rland Rdyields To estimate the gain-phase errors,the continuous multiplication operator(CMO)[15]is utilized.The(p,q)th element ofis expressed as wherep,q∈[1,M].Since the firstMcCOLD pairs have been calibrated,we have where. According to(10)and(11),we construct the following CMO as In practical applications,the covariance matrixis replaced by its sampled valueviaNsnapshots.Therefore,B1andB2in(13)are replaced by Remark 2.It can be seen that the adopted calibration scheme depends on the ULA structure.If the gainphase errors in the mth loop and dipole are different,we can also calibrate them successfully by applying CMO onRl andRd,respectively. Sparse recovery(SR)is chosen as a key technique for DOA estimation of polarized sources,since it holds the capacity of high resolution and great robustness to noise[17].With the estimated gain-phase errors,we compensate them as Subsequently,the DOA estimation problem can be cast as the followingℓ0-norm minimization problem Note that formulation(18)is a NP-hard problem and computationally infeasible.Alternatively,the researchers typically exploit theℓ1-norm to approximate theℓ0-norm and further construct a convex problem.However,it has been proven that the direct application ofℓ1-norm penalty will produce a biased estimation,since it penalizes larger coefficients more heavily than smaller coefficients[18]. In this paper,we exploit the log penalty to enforce sparsity,whose objective function is wheredenotes the log penalty with tuning parameterε >0,βis the regularization parameter,which can be properly selected via theL-curve method[19]or cross-validation scheme[20].As analyzed in[16],the log penalty is continuous and can approximateℓ0-norm very closely,which not only can yield a good estimation result,but also can be solved more efficiently in comparison with other penalties.To solve(19)efficiently,the DC decomposition technique is adopted,whose basic concept is to decompose a nonconvex function into two lower semi-continuous,proper convex functions,i.e., Finally,the optimization problem for DOA estimation is formulated as whereNote that(22)belong to the convex optimization framework,therefore their solutions can be easily achieved by some convex-type software packages such as CVX[21]. According to the estimated DOA information,the power of impinging source signals can be estimated by the following least square problem whose solution is Taking the same procedure on the following compensated vectors where We then obtain the polarization angle estimations as It has been proven by the literature[16]that the log penalty is a good approximation ofℓ0-norm penalty.In particular,when the tuning parameter is selected properly,the approximation error will become zero,which means that a good DOA estimation performance can be guaranteed.With such good DOA estimate,we deduce that a satisfactory estimation performance of other parameters can be easily achieved. In this section,the performance of the proposed method is investigated,and compared with those of the MODE method in[6],the SPS-ESPRIT method in[7],theℓ1-PSRCM method in[8]combined with our calibration strategy,as well as the Cram´er-Rao bound(CRB).A 7-element linear uniform COLD array withd=λ/2 is considered.Two sources are assumed to imping on the array from directionsθ1=−45◦,θ2=30◦with power informationand polarization information{γ1=20◦,η1=0◦},{γ2=40◦,η2=10◦}.The firstMc=4 COLD sensors are well calibrated,whereas the gain errors and phase errors in other sensors are generated by[10] whereξmandζmare independent and identically distributed random variables distributed uniformly over[−0.5,0.5],σρandσφare the standard deviations ofρmandφm,respectively.The estimation performance is evaluated by the root mean square error(RMSE),which is obtained by 500 independent Monte Carlo trails. In the first simulation,we evaluate the estimation performance of the proposed method in different SNRs.The standard deviations of gain errorsσρ,phase errorsσφand the number of snapshots are fixed at 0.1,40◦and 500,respectively,while SNR is varied from 0 dB to 20 dB.The RMSE curves are shown in Figure 2,from which we can see that the estimation performance of all parameters become better as the SNR increases.In addition,regardless of SNR,the performance of MODE and SPS-ESPRIT is not satisfied since the influence of array gain-phase errors.As a comparison,since the application of CMO and log penalty,the proposed method performs well and outperforms the compared methods in all SNR region for DOA estimation. In the second simulation,we show the effect of the number of snapshots on multi-parameters estimation performance.The SNR is set to 10 dB,whereas the number of snapshots is varied from 200 to 1000 in steps of 200.Other simulation conditions are the same as the first simulation.As can be seen in Figure 3,the RMSE of the proposed method decreases montionly as the number of snapshots,which is due to the fact that the sampled covariance matrix is closer to its true value as the number of snapshots increases.On the other hand,we can also observe from Figure 3(a)that the proposed method performs better than the compared methods,which is consistent with the conclusion obtained in the first simulation.This simulation efficient validate the superiorities of the proposed method. In the last simulation,we examine the negative influence of gain errors and phase errors on the performance of different methods.In Figure 4(a),σφ=40◦andσρvaries from 0.1 to 0.3,while in Figure 4(b),σρ=0.1,butσφvaries from 0◦to 50◦.The number of snapshots and SNR are set to 500 and 10 dB,respectively.From the simulation results,we can find that the proposed method performs almost independent of both gain errors and phase errors,and further provides a robust DOA estimation performance under the condition thatσφ ≥10◦.In contrast,the performance of the compared SPS-ESPRIT and MODE methods is mainly affected by the phase error seriously.When the phase errors are not large,they can supply a satisfied DOA estimation performance.However,if the phase errors exceed a certain threshold,their performance degrades tremendously. Figure 2.RMSEs of multi-parameters estimation versus SNR with the number of snapshots T=500.(a)DOA estimation.(b)Power and polarization parameters estimation. Figure 3.RMSEs of multi-parameters estimation versus the number of snapshots with SNR=10 dB.(a)DOA estimation.(b)Power and polarization parameters estimation. Figure 4.RMSEs of DOA estimation in different gain errors and phase errors with SNR=10 dB,T=500.(a)In different gain errors.(b)In different phase errors. In this paper,we proposed a new method for multiparameters estimation from sparse recovery perspective in the presence of gain-phase errors,where partly calibrated uniform liner COLD array is adopted.By properly using the continuous multiplication operator(CMO),log penalty as well as difference of convex(DC)functions decomposition,the proposed method not only provide an improved multi-parameter estimation performance in comparison with the other stateof-the-art methods,but also performs almost independent of gain-phase errors,which have been verified by several numerical simulations. This work was supported by the National Natural Science Foundation of China under Grant 61171137.III.PROPOSED METHOD
3.1 Gain-phase Errors Estimation
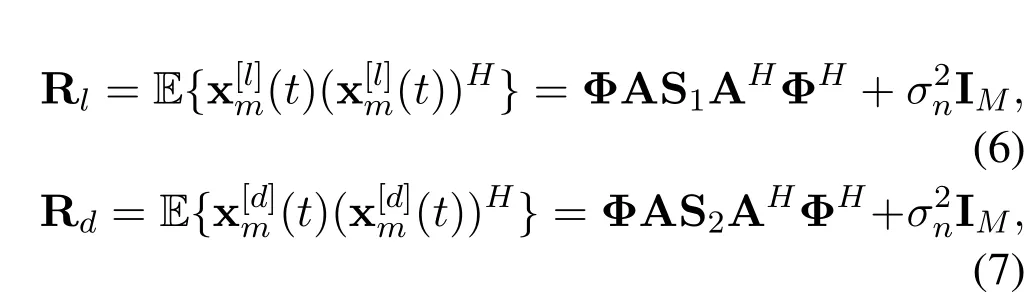

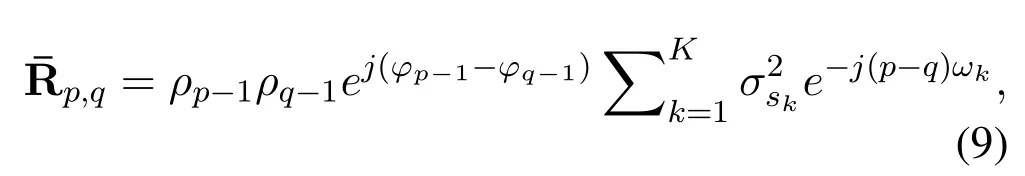
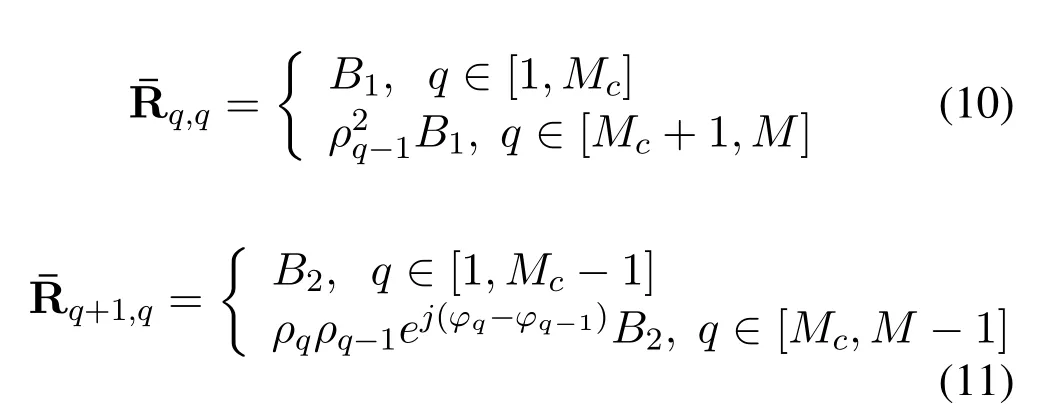
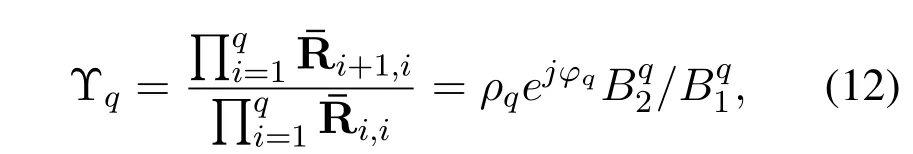
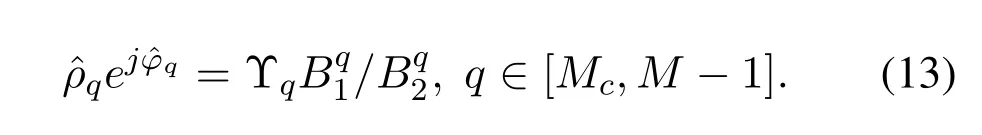
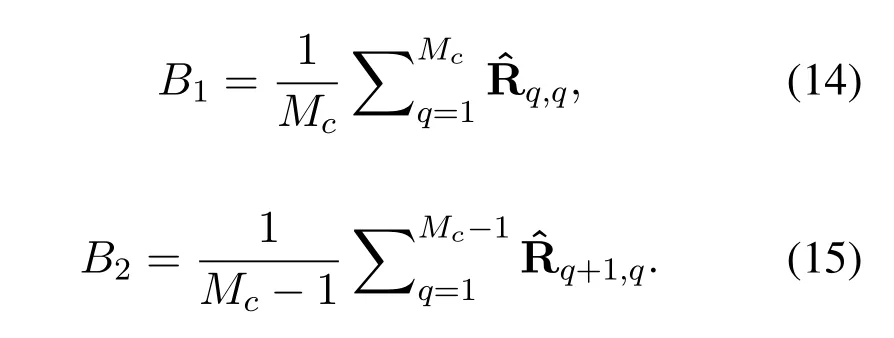
3.2 DOA Estimation Via Log Penalty
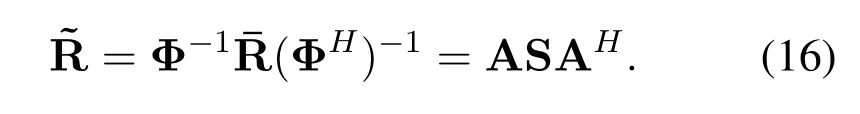

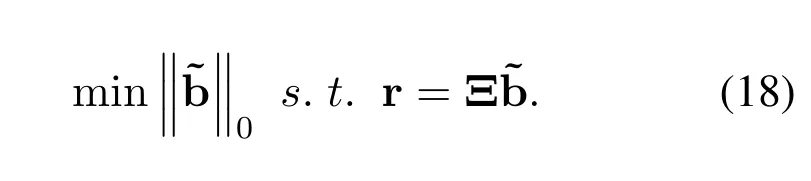
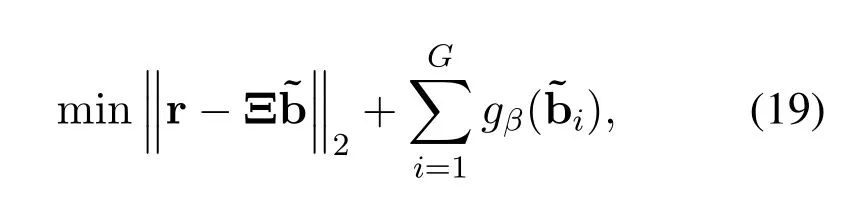
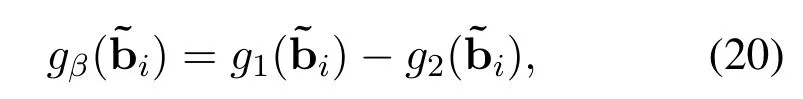
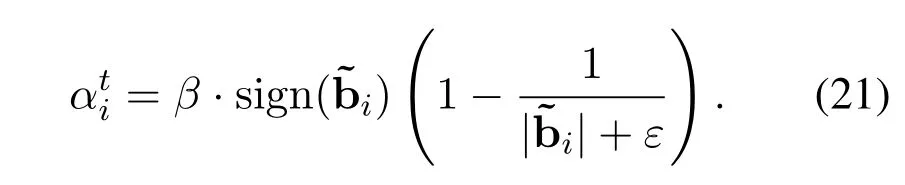
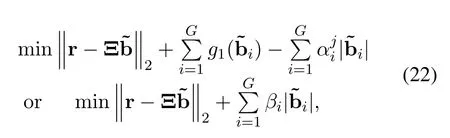
3.3 Power and Polarization Angle Estimation
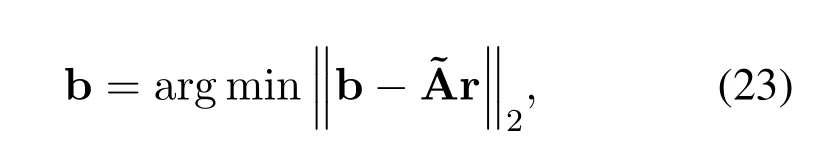


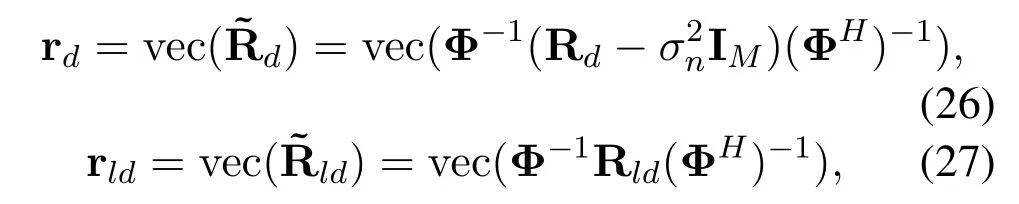
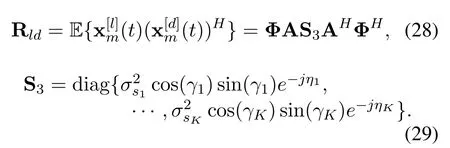
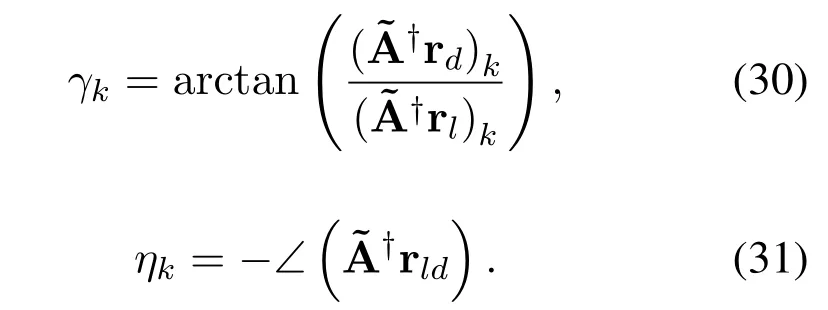
IV.SIMULATIONS
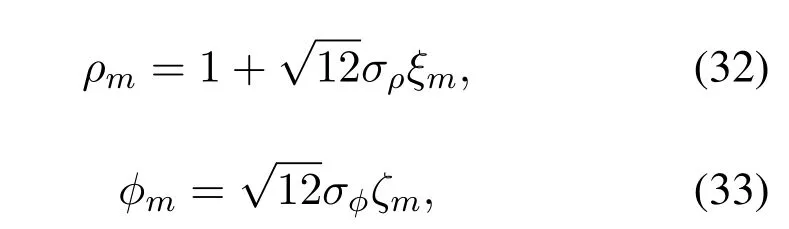
V.CONCLUSION
ACKNOWLEDGEMENT
- China Communications的其它文章
- Two-Timescale Online Learning of Joint User Association and Resource Scheduling in Dynamic Mobile EdgeComputing
- SHFuzz:A Hybrid Fuzzing Method Assisted by Static Analysis for Binary Programs
- SecIngress:An API Gateway Framework to Secure Cloud Applications Based on N-Variant System
- Generative Trapdoors for Public Key Cryptography Based on Automatic Entropy Optimization
- A Safe and Reliable Heterogeneous Controller Deployment Approach in SDN
- Distributed Asynchronous Learning for Multipath Data Transmission Based on P-DDQN

