基于固定点迭代的Huber鲁棒容积卡尔曼滤波算法

李 松，刘 哲，唐小妹，吴 健，王飞雪

国防科技大学 电子科学学院，长沙410073

非线性系统的状态估计是许多领域中广泛面临的问题，如目标跟踪、导航以及信号和图像处理[1]。扩展卡尔曼滤波（Extended Kalman Filter，EKF）通过一阶泰勒展开式的线性化过程来近似非线性系统，在工程中应用广泛。但是，当系统非线性较强时，其性能可能会降低甚至发散，因为EKF忽略了泰勒展开的高阶项，从而只能获得系统的一阶逼近精度[2]。粒子滤波[3]（Particle Filter，PF）作为一种序贯蒙特卡洛方法，通过大量的粒子来近似状态的概率分布，能够获得更高的估计精度，但其实时性较差且存在粒子退化和粒子贫乏等问题[4]。

为了提高非线性系统的估计精度，近年来，以无迹卡尔曼滤波[5]（Unscented Kalman Filter，UKF）和容积卡尔曼滤波[6]（Cubature Kalman Filter，CKF）为代表的基于确定性采样的方法受到广泛关注。与EKF不同，这类方法通过使用一组确定的加权采样点在非线性系统中传播[7]，能够精确地捕获非线性系统的统计特性，从而可以达到三阶的逼近精度[8]，并且这类方法无需计算雅克比矩阵，具有无需求导的优点。但是，UKF在处理高维系统时可能会不稳定，因为其中心采样点的权重可能为负[9]，为了避免非正定协方差矩阵的传播，需要对UKF中的参数进行仔细的调整[5]。与UKF不同，CKF使用一组等权重的容积点来计算非线性变换后随机变量的均值和协方差[6]，其估计精度和数值稳定性均优于UKF，尤其是在处理高维非线性系统时[9-10]。

然而，UKF与CKF本质上都是基于最小化误差的l2范数的原则，即基于最小均方误差（Minimum Mean Square Error，MMSE）准则进行推导[11]，因此当误差的实际分布与假设的高斯分布不相符时，两者的性能都会随之下降[12]。Huber[13]提出一种基于最小化误差的l1/l2范数的方法（即Huber方法），通过使得最大渐进估计的方差最小，能够提高系统在干扰高斯分布的噪声下的鲁棒性，因此该方法的鲁棒性优于基于l2范数的估计方法[14]。Karlgaard等[15]将量测方程进行线性化，并将Huber方法应用于差分滤波。Wang等[16]同样采用线性化的方法将Huber方法应用于UKF。通过将Huber方法应用于非线性滤波算法，证明了该方法能够增强滤波算法在非高斯噪声下的鲁棒性。Chang等[17]指出利用Huber方法重构量测信息（量测噪声协方差矩阵）能够使得滤波算法更加鲁棒。秦康等[12]从贝叶斯估计的角度解释了Huber方法使滤波算法鲁棒的原因是通过对新息进行截断平均。

如前所述，CKF相比于UKF而言估计精度和数值稳定性更好，因此本文将Huber方法应用于CKF中。首先通过对量测方程进行线性化近似，将系统方程构造为线性回归模型，然后采用固定点迭代的方法求解基于Huber方法的最小化问题，推导了基于固定点迭代的Huber鲁棒CKF（Fixed-Point Iterated Huber-based robust Cubature Kalman Filter，FP-IHCKF）算法。分析算法可以看出，Huber方法重构了量测更新过程中的先验信息和量测信息，使得所提算法能够减轻非高斯噪声对于状态估计的影响。对再入目标跟踪问题进行仿真，仿真结果表明，与传统方法相比，所提算法在非高斯噪声下鲁棒性更强且估计精度更高。

1 容积卡尔曼滤波算法

考虑如下离散非线性系统：

其中，下标k≥0为离散化时间；xk∈ℝn和zk∈ℝm分别为状态向量和量测向量；f(⋅)和h(⋅)分别为非线性的状态转移函数和量测函数；wk-1∈ℝn和vk∈ℝm分别为过程噪声和量测噪声，假定两者为相互独立的零均值高斯白噪声，并满足：

其中，Qk和Rk分别为过程噪声和量测噪声的协方差矩阵。

CKF算法通过在给定模型中传播一组等权重的容积点来实现非线性变换，其滤波过程可以总结如下：

（1）滤波初始化

设置滤波初值x̂0及相应的误差协方差矩阵P0：

（2）时间更新

①计算基本容积点ςi：

其中，ei表示n×n维单位矩阵的第i列。

②基于滤波值x̂k-1计算容积点Xi,k-1：

④计算k时刻的状态预测值x̂k/k-1及相应的误差协方差矩阵Pk/k-1：

（3）量测更新

①基于预测值x̂k/k-1计算容积点Xi,k/k-1：

②计算在量测方程中传播后的容积点Zi,k/k-1：

③计算k时刻的量测预测值ẑk/k-1、新息协方差矩阵Pzz,k/k-1以及互相关协方差矩阵Pxz,k/k-1：

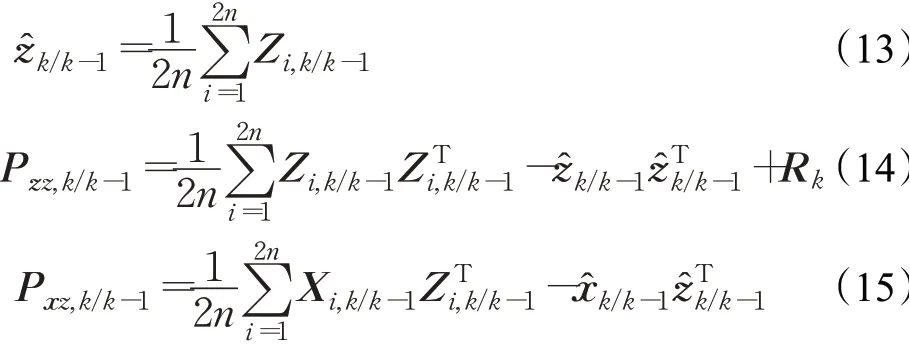
④计算k时刻的状态估计值x̂k及相应的误差协方差矩阵Pk：

2 基于Huber方法的鲁棒CKF

2.1 线性回归模型

在状态预测值x̂k/k-1处对式（1）中的量测方程进行线性化近似得：其中为线性化量测矩阵。

因此，基于式（1）表示的非线性系统，可构造如下线性回归模型：

注意到，式（19）中Hk为EKF中使用的线性化量测矩阵，考虑到统计线性化量测矩阵可以由式（15）和式（9）求得，具有无需求导且能够保留CKF高估计精度的优点，因此本文用Hˉk代替Hk。根据统计线性化量测矩阵Hˉk可得量测协方差矩阵为：

而由文献[17]知，CKF的量测协方差矩阵为：

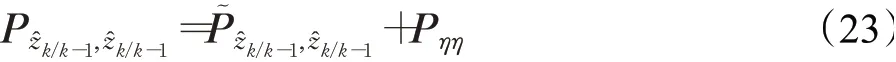
其中，Pηη为统计线性化误差协方差矩阵。因此，直接使用Hˉk来完成后续的量测更新实际上会导致协方差传递过程中的精度损失[18]，从而降低滤波算法的估计精度[12，17，19]。为避免此问题，对量测噪声的协方差矩阵进行如下修改[20]：

因此，φk的协方差矩阵修改为：

其中，

2.2 基于Huber方法的估计准则

KF和CKF本质上都是基于MMSE准则，即x̂k通过最小化如下的l2范数得到：

其中，ξk,i为ξk的第i个分量。因此CKF无法有效应对非高斯噪声的情况，在实际工程应用中，若噪声不满足高斯分布的假设，则CKF的估计精度将降低甚至发散。

为了增强滤波算法的鲁棒性，x̂k可通过最小化如下的代价函数得到：

其中，ρ(⋅)为有界凸函数。故随着残差ξk,i增大，ρ函数不会像l2范数一样迅速增长，因此幅度较大的、偏离高斯分布的异常值在代价函数中的权重相对更小，从而可以减轻状态估计值对于非高斯噪声的敏感程度，使得滤波算法更加鲁棒。常用的ρ函数为如下所示的Huber函数[21]：

其中，γ为调节因子，通常可取为1.345[22]。对于较小的τ,ρ函数具有l2范数的特点，因此能够保证高斯噪声下的估计精度，而对于较大的τ,ρ函数增长较为缓慢，因此能够抑制异常值和重尾噪声的影响[23]。Huber函数结合了最小l1范数估计的鲁棒性和最小l2范数估计的诸多优势，鲁棒性较强[11]。

2.3 FP-IHCKF算法推导

对式（31）关于xk求偏导，并令其为0得：

因此，式（33）可以进一步写为：

根据式（26）知ξk=yk-Mk xk，因此式（35）可进一步写为如下的矩阵形式：

由式（36）可得：

其中，

xk通常未知，而由式（34）可知Ψk是关于xk的函数，因此式（37）本质上是一个关于xk的迭代方程：

本文采用固定点迭代的方法求解式（37），即

将式（25）、（27）、（28）和（38）代入式（37）可进一步得：

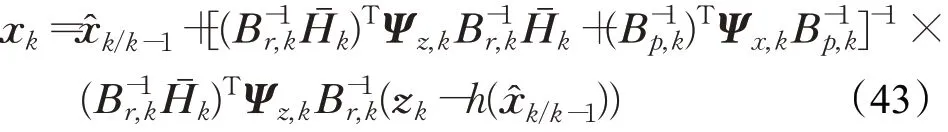
定义如下变量：

并将其代入式（43）得：

对式（45）使用矩阵求逆引理，式（45）可等效为下式：

其中，

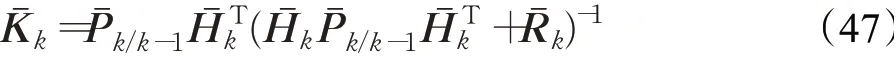
通过上述分析，可将FP-IHCKF算法流程总结如下：

（1）滤波初始化

同传统CKF一样，利用式（3）设置滤波初值。

（2）时间更新

同传统CKF一样，利用式（4）~式（9）完成时间更新过程。

（3）量测更新

①令迭代次数为t=1，并设初始迭代估计值，其中表示第t次迭代时的估计值；

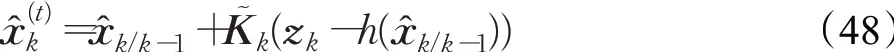
其中，

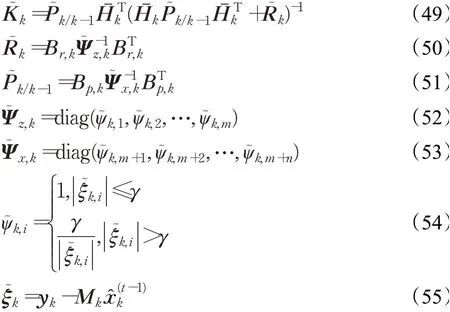
其中，In为n×n维单位矩阵；‖ ‖x表示求取向量x的二范数；ϵ为迭代门限，本文取ϵ=10-5。

2.4 算法收敛性及鲁棒性分析

文献[24]表明，如果ψ函数不增加（对于ξk,i>0），则迭代过程将收敛，而式（32）中使用的ρ函数能够满足该条件。值得说明的是，当γ→∞时，式（32）中的Huber函数退化为l2范数的形式，且FP-IHCKF也退化为CKF。此时，Ψk→I，式（36）仅需一次迭代过程即可求解。

从FP-IHCKF算法流程可以看出，所提算法采用迭代的方式进行量测更新，在迭代过程中通过ψ函数重构了先验信息Pk/k-1和量测信息Rk，使得在偏离高斯分布的异常值出现时，滤波算法能够相应地调整对于状态预测值和量测值的置信度，进而降低异常值在滤波中的“贡献”，从而能够减轻非高斯噪声对于状态估计的影响，使得算法更加鲁棒。特别地，当仅有量测噪声非高斯时，所提算法可以只迭代一次，此时仅有量测信息被重构。

需要注意的是，在FP-IHCKF中新息为zk-h(x̂k/k-1)（式（48））而在CKF中新息为zk-ẑk/k-1（式（17）），因此这里没有利用到非线性变换的优势。对于非线性较强的量测方程而言，将FP-IHCKF中的新息替换成zk-ẑk/k-1能够进一步提高估计精度，本文对此不做进一步讨论。

3 仿真与分析

3.1 仿真模型

对再入目标跟踪问题[25]进行仿真，仿真示意图如图1所示。目的是估计目标从很高的高度高速重新进入大气时的位置xt(1)（单位ft）、速度xt(2)（单位ft/s）以及一个常值系数xt(3)（单位1/s）。状态方程为：

图1 再入目标跟踪问题示意图Fig.1 Diagram of re-entry target tracking problem

其中，[wt(1),wt(2),wt(3)]T为高斯白噪声，其协方差Q=0；常值ρ0=2为海平面的空气密度；k=2×104为定义空气密度和高度间关系的一个常数；g=32.2 ft/s2为重力加速度。

对式（57）中的状态方程ẋt=g(xt)采用欧拉积分法，以步长Δt=0.01 s进行离散化，即：

测量雷达测量其到目标之间的距离。

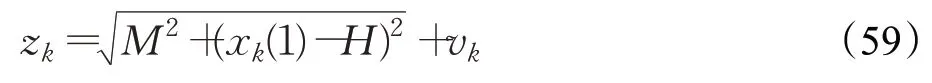
量测方程为：其中，雷达的高度为H=105ft；雷达到目标下降铅垂线的水平距离为M=105ft；vk为量测噪声。

仿真中，雷达量测周期为T=0.5 s。初始状态真实值和估计值以及初始误差协方差矩阵分别为：

3.2 对比实验

为了比较算法性能，采用均方根误差（Root Mean Square Error，RMSE）以及时间平均RMSE（Time-Averaged RMSE，TARMSE）作为评估指标。RMSE和TARMSE分别定义为：

分别比较以下几种算法：PF（粒子数为1 000）、EKF、Huber-EKF（HEKF）、CKF以及本文的FP-IHCKF。为了比较不同线性化量测矩阵的影响，FP-IHCKF考虑两种情况，采用线性化量测矩阵记为FPIHCKF1，采用统计线性化量测矩阵记为FP-IHCKF2。

首先，假定量测噪声服从如下高斯分布：

图2 ~图4给出了高斯噪声下各算法的RMSE结果。由于各算法在30 s后趋于稳定，故计算30~60 s的TARMSE结果，由于T=0.5 s，因此k1=60，k2=120，TARMSE结果如表1所示。

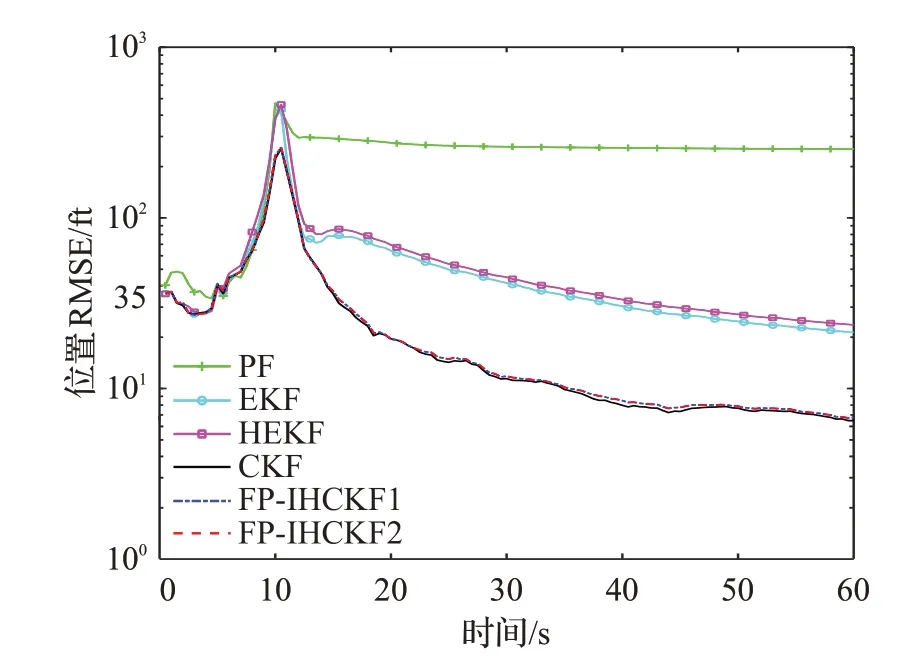
图2 高斯噪声下的位置RMSEFig.2 RMSE of position under Gaussian noise

图3 高斯噪声下的速度RMSEFig.3 RMSE of velocity under Gaussian noise

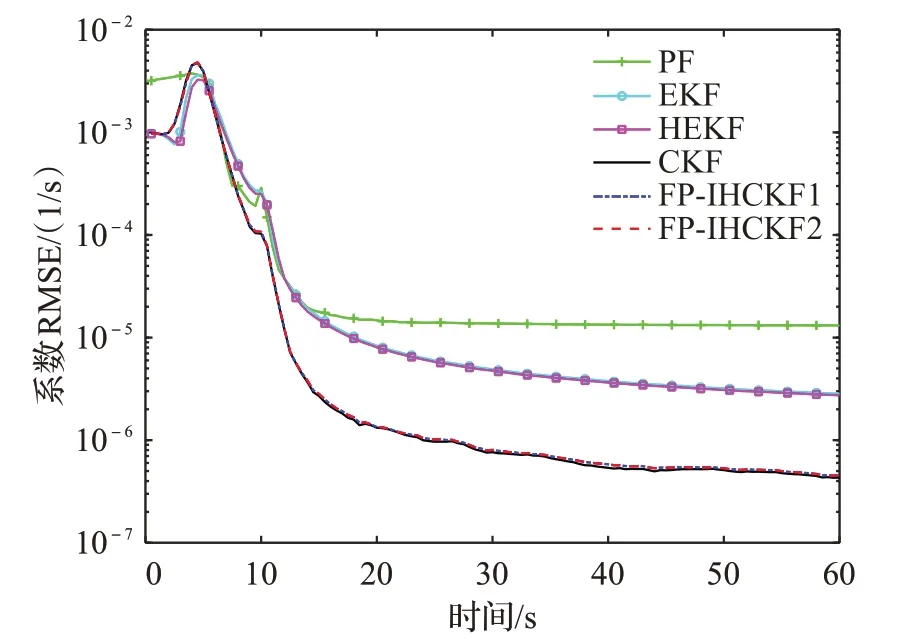
图4 高斯噪声下的系数RMSEFig.4 RMSE of coefficient under Gaussian noise

表1 高斯噪声下各算法TARMSETable 1 TARMSE for each algorithm under Gaussian noise

从图2~图4和表1可以看出，PF对目标位置的估计性能表现较差，造成这种情况的一个可能原因是，当无法直接测量某些状态量时，PF可能表现不佳（在仿真中，只有雷达到目标的距离被测量）。CKF和FP-IHCKF相比于EKF和HEKF而言，估计精度更高。FP-IHCKF2的估计精度优于FP-IHCKF1，这是因为前者能够更好地保留CKF高估计精度的优点。注意到，HEKF和FPIHCKF的估计精度稍差于EKF和CKF，这是因为后两者基于MMSE准则，能够在高斯噪声条件下得到最优的估计性能，而前两者采用Huber代价函数推导得到，因此在高斯噪声条件下是次优的。

接着，假定量测噪声服从如下高斯混合分布：

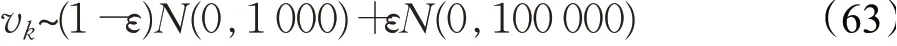
其中，ε为混合高斯分布中的干扰因子[11]，本文取ε=0.1。

图5 ~图7给出了非高斯噪声下各算法的RMSE结果，TARMSE结果如表2所示。

图5 非高斯噪声下的位置RMSEFig.5 RMSE of position under non-Gaussian noise

图6 非高斯噪声下的速度RMSEFig.6 RMSE of velocity under non-Gaussian noise

图7 非高斯噪声下的系数RMSEFig.7 RMSE of coefficient under non-Gaussian noise

表2 非高斯噪声下各算法TARMSETable 2 TARMSE for each algorithm under non-Gaussian noise

从图5~图7和表2可以看出，EKF和CKF的估计精度相比于高斯噪声条件下明显降低。PF相对而言受到的影响较小，但其对于位置的估计性能仍然不佳。HEKF和FP-IHCKF相比于EKF和CKF而言估计精度更高，证明了这些算法在非高斯噪声条件下的鲁棒性。FPIHCKF2仍然能够获得优于FP-IHCKF1的估计性能。

下面比较上述几种算法的计算复杂度，仿真软件为MATLAB，所有算法均运行于处理器为Intel Core i5-4200H（2.80 GHz）、内存为8 GB的PC上。设CKF的运算时间为1，各算法的相对运算时间如表3所示。

表3 各算法相对CKF的运算时间Table 3 CKF-relative computation ratios

从表3可以看出，EKF消耗的运算时间最少，PF消耗的运算时间最多。HEKF和FP-IHCKF相比于EKF和CKF而言，消耗的运算时间更多，这是因为这两者的量测更新中增加了额外的计算。注意到，FP-IHCKF2消耗的运算时间多于FP-IHCKF1，这是因为FP-IHCKF2采用的是统计线性化量测矩阵，而FP-IHCKF1采用的是线性化量测矩阵，前者的量测更新中涉及到2n个容积点的运算，能更好地保留CKF高估计精度的优点，但是以略微牺牲计算复杂度为代价的。

4 结束语

针对非高斯噪声下CKF估计精度下降的问题，本文将Huber方法应用于CKF框架中，并采用固定点迭代的方法求解状态的后验估计值，提出了FP-IHCKF算法。与传统方法不同，所提算法结合了CKF算法高估计精度以及Huber方法鲁棒性的优点。算法理论分析与仿真实验结果验证了所提算法的有效性和鲁棒性。