基于分群解耦的电力系统机电电磁混合仿真的分网技术

穆清，程昱，王春明，汪旸，严剑峰，徐得超，庞润甜

（1.电网安全与节能国家重点实验室（中国电力科学研究院有限公司），北京市海淀区100192；2.国家电网有限公司华中分部，湖北省武汉市430014）

0 引言

随着碳减排和环境治理的压力，电力系统的运行模式发生了巨大的变化。电源从负荷集中的东部沿海地区快速向水电等清洁能源丰富的西部地区转移，同时风电等新能源发电的快速发展也加速了这一转移过程[1]。电源和负荷异地设置不仅引起区域电力不平衡，也产生了大量的跨区超远距离送电需求。国家电网公司建立了强交强直的智能特高压电网解决超远距离大规模送电问题，实现了跨越数千km的电力平衡。特高压电网中含直流输电30多条，承担了西部电源地区水电、风电等大量清洁能源的电网接入，为我国清洁能源利用做出了巨大贡献[2]。2017年迎丰度夏时，接入华东地区的8条直流输电系统输电容量达到4.7 GW，占上海地区用电负荷的30%[3]。

当前主流的电力系统仿真工具主要有两种：机电暂态仿真工具和电磁暂态仿真工具。机电暂态仿真广泛应用于电力系统的各个领域[4-5]。然而，随着电力电子设备在电力系统中的广泛应用，基于电网换相整流器高压直流输电技术（linecommutated converter based high voltage direct current,LCC-HVDC）和以全控型器件为基础的电压源换流器高压直流输电（voltage source converter based high voltage direct current,VSC-HVDC）承担互连和跨区域传输。在机电暂态仿真中，电力电子转换器瞬态过程模拟精度不足的缺陷开始变得更加显著。错过或误判由换相失败引起的严重电网故障，使得机电暂态仿真系统不再准确，给电力系统的运行控制带来了困难[6]。电磁暂态仿真系统可以准确描述设备的内部瞬态过程，仿真电力电子变换器比较准确[7]。因此，电磁暂态仿真系统在电力电子设备和电网分析中得到广泛应用。然而，由于电磁暂态仿真采用非常小的时间尺度（步长），仿真计算的时间成本很高，并且整个网络中数万个节点的电磁暂态仿真会带来天文级的计算时间消耗，这在实际应用中难以接受[8]。

机电–电磁混合仿真是将具有缓慢动态的交流电网放入机电子网；将直流和其他电力电子系统等具有快速动态的部分电网放入电磁暂态子网中。该方法结合了机电暂态仿真和电磁暂态仿真的优点，弥补了它们的不足，成为解决新一代电网仿真的优秀解决方案[9]。

Reeve和Adapa提出将混合仿真接口扩展到交流系统内部，这样允许接口形式的灵活性，并可避免由接口中的严重波形失真和相位不平衡引起的误差。但是，该方法需要迭代[10]。Anderson提出了通过频率相关的等效阻抗电路来表示机电侧的方法，解决了混合仿真中界面波形失真和相位不平衡的问题。同时，基波提取方法将电磁暂态(electromagnetic transient,EMT)侧 的瞬时数 据转换为机电暂态(stability transient,ST)侧所需的基本相位相量。但是，在具有许多接口的大型电网中求频率相关等效的电路是非常困难的，计算量也很大[11]。文献[12]提出了一种基于机电暂态侧3序等效的等效机电–电磁混合仿真方法，并提出了一种基本负序电流补偿的修正算法，避免了由于正序参数和负序参数不等而引起的电磁暂态网络矩阵的不对称。但是，该算法仅针对单个电磁暂态网络进行优化，不能实现并行。中国电力科学研究院基于节点分裂多尺度机电–电磁混合仿真算法，自主开发了ADPSS混合仿真平台。算法不用考虑接口位置和接口元件，并实现了机电子网和等效电磁子网的并行同步。然而，对大型电磁暂态网络的计算效率依旧很低[13]。

本文在ADPSS机电–电磁暂态混合仿真平台的基础上，提出了一种多层机电–电磁混合仿真并行仿真方法，该方法不仅保证了仿真精度，而且通过网络解耦元件大大降低了仿真的计算时间消耗。本文的研究成果是在ADPSS仿真平台上开发的，在国家电网运行模式的计算中得到了验证。

1 机电–电磁混合仿真的接口方法

1.1 机电-电磁混合仿真的接口电路及算法

本文采用的机电暂态–电磁暂态混合仿真接口的等值电路如图1所示。计算电磁暂态网络时，将机电暂态网络进行戴维南等值；计算机电暂态网络时，将电磁暂态网络进行诺顿等值。

图1 机电–电磁暂态仿真的等值电路Fig.1 Equivalent circuits of electromechanicalelectromagnetic transient simulation

具体接口算法为：在电磁侧零时刻初始化时，根据全网初始状态计算得到机电暂态网络的等值阻抗阵ZST和电磁暂态网络的等值导纳阵YEMT。在每一个接口时刻，机电暂态网络向电磁暂态网络发送正、负、零序等值电势EST。若机电暂态网络拓扑变化还需要重新发送等值阻抗阵ZST。电磁侧网络合并了机电暂态网络的等值电路（EST和ZST）进行求解，获得电磁暂态网路的全网状态量及接口处的母线电压和接口电流的状态量。

同时，电磁暂态网络根据暂态量及接口处的母线电压和接口电流的暂态量进行正负零序的转换，获取接口处正、负、零序电压UEMT和电流I'EMT，并向机电暂态网络发送。机电暂态网络收到后按照电磁侧等值导纳阵不变的假定求解IEMT

然后将电磁侧网络等值电路的注入电流IEMT和导纳阵YEMT合并到网络方程中进行求解，即可得到机电暂态全网状态量。

1.2 机电-电磁混合仿真电磁侧的网络分解算法

对于电磁暂态网络，当机电侧发电机正、负序阻抗不相等或母线带有动态特性综合负荷时，戴维南等值阻抗阵ZST转换到ABC相空间上是不对称矩阵，与电磁暂态仿真的基本算法矛盾，无法直接合并到电磁暂态网络方程中进行求解。

针对这个问题，ADPSS仿真系统采用了节点分裂算法单独计算电磁暂态网络与机电暂态等值网络的边界点电流Ia。此处直接引用文献[14]中推导的边界点电流求解公式

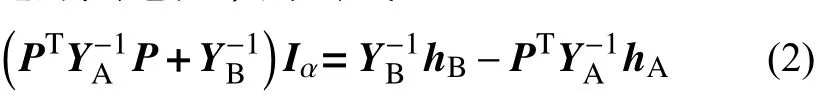
其中：YA、YB分别为电磁网络和机电等值网络的导纳阵；hA、hB分别为电磁网络和机电等值网络的等值历史电流源；P为反映电磁网络所有节点与边界电流相量的关联关系矩阵。需要注意的是，式(2)是根据电磁暂态（electro magnetic transient program,EMTP）算法推导的接口电路方程，所有状态量均为瞬时值。直接求解式(2)中的电磁网络导纳阵逆矩阵YA−1的计算量太大，实际计算采用了戴维南等值简化法求解PTYA−1P，其计算量与混合仿真接口数目相关[14]。

2 机电-电磁混合仿真的分群解耦技术

由于机电暂态10 ms才进行一次计算，因此整个机电–电磁混合仿真的关键计算量在电磁暂态网络计算和机电暂态等值网络接口计算，实现这些部分计算的高效运行成为研究的核心问题。

式(2)中接口矩阵YA包含了整个电磁网络的导纳阵，当电磁暂态网络的规模越来越大时，式(2)中接口矩阵PTYA−1P计算量将呈现指数级别的增加。同时式(2)的接口矩阵YA包含了整个电磁网络的所有导纳元素，给电磁暂态的分网解耦算法带来了巨大的挑战。本文提出了基于机电–电磁整体网络的分群解耦算法。

2.1 机电-电磁混合仿真电磁侧的解耦技术

传统的电磁暂态计算采用传输线对电磁暂态网路进行分网解耦[15]。传输线解耦，在数学上将表征为传输线相连的两个电气节点之间没有互联的导纳元素，而只通过注入的历史电流源相互关联。

通过传输线解耦以后，整个电磁暂态网络将分为导纳阵解耦的多个电磁暂态子网络。这些电磁暂态子网络在单步仿真上可以看成完全解耦的电磁暂态孤岛。

通过节点重排，YA可以表示为如下的矩阵：

其中YA1到YAn表示n个电磁暂态网络孤岛的内部导纳阵。

由此式(3)代入式(2)可得式(4)：

2.2 机电-电磁混合仿真机电侧的解耦技术

由式(4)可知，电磁暂态子网络矩阵已经简化为对角矩阵形式。本节将简化机电侧接口的机电等值网络导纳矩阵YB。

假设机电暂态网络可以从物理上分割为m个独立的孤岛。由于机电暂态的孤岛是完全物理隔离的，如果孤岛还没有与电磁暂态子网的接口，那么次子网必然对系统其他部分没有任何影响，在整个算法中可以不考虑。由此，可以假设m个电气孤岛必然都含有与电磁暂态子网的接口。

通过节点重排，YB可以表示为如下的矩阵：

其中YB1到YBm表示m个机电暂态网络孤岛的内部导纳阵。

由此式(5)代入式(4)可得式(6)：

根据式(6)可知，如果电磁暂态网络导纳矩阵YAn和机电等值网络的分块矩阵YBm之间阶数关系能够匹配，即数个YAn和数个YBm的阶数相加正好完全吻合，则式(6)就可以变成多个独立的解耦方程，进行并行求解。

这个性质从物理上看就是，整个电磁侧的计算网络（包含了机电暂态等值系统）可以根据接口的联络关系把机电侧的等值网络孤岛和电磁暂态的传输线分割出的孤岛组合成多个完全相互不联系的孤岛。这些孤岛都能进行并行求解，大幅降低了并行混合仿真的计算量。

2.3 机电-电磁混合仿真的分群解耦算法

一般来说一个机电暂态孤岛能对应一个或几个电磁暂态孤岛，并形成网络拓扑关系上的电气解耦网络。但是如果机电暂态孤岛中对应了多个电磁暂态孤岛，而这些电磁暂态孤岛又连接其他的机电暂态子网群时候，对整个电路的拓扑分析和组合就成为一个关键问题。

本文研究了对于这种复杂特殊网络结构的处理方法：①如果电磁端是数个独立孤岛连接一个机电孤岛子网，这种模式将把这几个连接相同机电孤岛子网的电磁孤岛合并到一个大的电磁孤岛进行处理。②如果电磁端是一个独立孤岛连接数个机电孤岛子网，这种情况下，数个机电孤岛子网合并为一个机电孤岛统一进行电磁机电混合仿真。③如果是多个两层以上的结构：一个电磁孤岛连接两个以上的机电孤岛，这几个机电孤岛再与其他电磁孤岛相连，则这些所有的电磁孤岛和机电孤岛子网全部合并处理。

由此可知，综合上述分网规则可以建立如下系统分网原则：①机电系统通过有没有“机电侧电气连接”的标准划分为数个孤岛，电磁系统侧根据传输线分网划分为数个解耦的电磁孤岛。②根据机电–电磁混合仿真接口的连接关系，把通过机电–电磁混合仿真接口相互电气连接的所有的数个机电孤岛和电磁孤岛划分为一个统一的机电–电磁混合仿真子网组。

子网组内包含一个大机电孤岛和一个大电磁孤岛。本文定义此子网组为一个机电–电磁混合仿真的子网群，子网群中的大电磁孤岛定义为一个电磁子网群，其大机电孤岛定义为一个机电子网群。

显然电磁子网群内部可能包含多个原始的电磁传输线分割的孤岛，我们定义子网群内部的电磁传输线分割的孤岛为电磁暂态子网。同理，机电子网群内部可能包含多个原始的机电物理分割的孤岛，我们定义子网群内部的孤岛为机电暂态子网。为了实现子网群内部的协调计算(例如式(2))，子网群内部设立一个机电主控和电磁主控，主控的计算任务归并到含有最多机电–电磁混合仿真接口的子网中。

分群解耦的机电电磁混合仿真分群方法如图2所示，整个电力系统的电磁暂态部分被分成m个电磁暂态孤岛子网群（EMT group land system），表示为1到m。每个子网群拥有一些电力系统电磁暂态子网，表示为EMTSub1到EMTSubm。所有电力系统电磁暂态子网都分布在各个电力系统群内，且只能属于一个唯一子网群。每个子网群有且只有一个主控子网（深色网格子网），负责与子网群层相关的协调和计算工作。

图2 分群解耦的机电电磁混合仿真分群方法Fig.2 Group division technology for group decoupled EMT-ST hybrid simulation

电力系统的机电暂态部分也组成了独立的子网群(ST land system)。此子网群是孤岛性的机电子网，并不是分网并行的机电子网。每一个机电孤岛子网与一个电磁子网群相连。

3 适应分群解耦的机电–电磁混合仿真软硬件系统架构

基于高性能服务器运算架构（HPC）体系的电力系统仿真是未来的重要发展方向。此体系是通过巨量的CPU同时参与计算，提升整体的计算能力。虽然单一CPU的计算能力不是非常强，但是每一个计算任务的CPU使用数量可以达到成百上千个，整体计算性能非常可观。

基于适应HPC的计算特点，混合仿真的软硬件系统架构的主要设计目标是通过并行算法把电力系统分成均衡的小份，把每一小份电力系统放在独立的CPU上运行。不同小份之间通过调用CPU的核间通信完成信号传递。

分群解耦机电–电磁混合仿真的软硬件系统架构已经在中国电科院的ADPSS软件系统上布置，实现机电–电磁混合仿真的并行高效计算。

机电-电磁并行仿真新架构如图3所示，并行仿真整体结构分为4个层级，第1个层级是任务层，任务层分为电磁暂态计算(电磁)，机电暂态计算(机电)。

图3 机电-电磁并行仿真新架构Fig.3 A new Architecture for EMT-ST hybrid simulation

对于电磁暂态任务来说，其第2层为子网群层。子网群是一些在拓扑上密切相关的电力系统子网集合，拓扑关系非常紧密。子网群的划分将依据电力系统之间的耦合情况，只有开断的和能通过解耦元件完全解耦的电路才能作为子网群分割。每个电磁暂态任务可以包括多个子网群。

电磁暂态计算的第3层是子网层，子网层包括了所有独立的电磁暂态子网和机电暂态子网的计算。电磁暂态子网是电磁暂态仿真计算的基本单元，子网计算包括了求解网络方程、更新历史电流源、更新系统网络状态等完整电磁暂态计算流程。每一个子网群包含一个及以上的子网。

第4层是物理CPU元件层，包含了ADPSS已经配置的所有可用物理CPU核。由于实时仿真计算要求CPU计算的硬实时性，为了避免进程调度对仿真计算实时性的影响（因为进程切换会带来内存加载和释放，引起缓存丢失），ADPSS把承载一个子网计算的一个进程绑定到一个CPU上，防止进程调度的出现。

4 案例研究

ADPSS电力系统数字实时仿真系统已经在国调、分调和省调的电力系统方式计算、电力系统故障反演等多个方面获得了广泛的应用。随着本文提出的交叉电力系统分网算法的应用，方式计算等使用混合仿真计算的应用场景获得了明显的加速提升。

国调冬滚的方式计算系统结构如图4所示。其中，交流部分采用了机电暂态进行仿真，直流输电部分，一共7回直流采用了电磁暂态进行仿真。系统的规模见表1和表2。

表1 机电暂态部分网络规模Table 1 Ne twork scale of the ST part

表2 电磁暂态部分网络规模Table 2 Network scale of the EMT part

图4 国调冬滚的方式计算系统结构Fig.4 System structure of State Grid Dispatching Center’s winter roll-up calculation mode

4.1 传统机电–电磁混合仿真与并行仿真精度比较

按照新算法，电磁暂态网络可以按照单条直流进行分网，清晰地分为7个子网，ADPSS仿真平台上的分网以后的结果见图5。

图5 算例系统分群解耦方案Fig.5 The grouping decoupling scheme utilized in calculation example

在电磁暂态分网情况下，7个电磁暂态子网分为2个群，其中子网1，子网2，子网6，子网4为群1，子网3，子网5，子网7属于群2。

通过比较传统机电–电磁混合仿真和基于分群解耦机电–电磁混合仿真间的波形可验证所提出的基于分群解耦机电–电磁混合仿真的精度。

传统混合仿真与新算法的直流电压瞬时值比较见图6，由图可见两种仿真模拟中的直流电压仿真结果完全一致。图7所示的传统混合仿真与新算法的熄弧角比较表明两种仿真方法的触发角几乎相同。因此，基于分群解耦的机电–电磁混合仿真算法与传统的机电–电磁混合仿真具有相同的结果。

图6 传统混合仿真与新算法的直流电压瞬时值比较Fig.6 Comparison of DC voltage instantaneous value obtained by traditional hybrid simulation and the new algorithm respectively

图7 传统混合仿真与新算法的熄弧角比较Fig.7 Comparison of extinction angle obtained by traditional hybrid simulation and the new algorithm respectively

4.2 传统机电-电磁混合仿真与并行仿真效率比较

图8 为不同混合仿真计算模式的计算时间比较，由图可知，现有机电–电磁混合仿真的电磁暂态侧的单步计算时间（仿真步长50μs）为0.026 s；基于分群解耦的机电–电磁混合仿真模式时，单步计算时间为0.0007 s，加速比为37.5。

图8 不同混合仿真计算模式的计算时间比较Fig.8 Computing time comparison of different hybrid simulation modes

5 结论

本文提出的基于分群解耦的机电–电磁混合仿真分网技术在不损失精度的情况下将仿真任务加速35倍以上。

本文提出了一种新的基于分群解耦的机电–电磁混合仿真技术，大大提高了机电–电磁混合仿真的仿真速度。机电暂态网络尽可能地划分为电气孤岛，而电磁暂态网络由传统的传输线和电力节点划分的子网组成电磁暂态子网群。为了划分子网群，本文提出了一种算法来形成基于分群解耦的机电–电磁暂态子网群，它们之间没有耦合。然后，提出了一种新的并行系统架构，实现了与电磁暂态网络组和机电暂态网络组的并行仿真，加快了仿真速度。以电网调度的电力运行方式为例，包括7个直流输电线路和4000个节点的电磁暂态网络，表明该方法可以在不降低精度的情况下大大提高仿真速度。本文的研究成果是在ADPSS中开发的仿真平台，在国家电网运行模式计算中得到验证。