基于拉格朗日插值法的概率建模方法及其在概率潮流分析中的应用

杨少瑜，黄国栋，林星宇，乐彦婷，唐俊杰

（1.重庆理工大学电气与电子工程学院，重庆市巴南区400054；2.中国电力科学研究院有限公司，北京市海淀区100192；3.输配电装备及系统安全与新技术国家重点实验室(重庆大学)，重庆市沙坪坝区400044）

0 引言

截至2018年，全世界范围内可再生能源发电的装机容量占总装机容量的33%以上，可再生能源全年发电量约占全球总发电量的26.2%，其中风力发电所占全球总发电的比例超过5%[1]。

随着大量可再生能源的并网，风速、太阳辐射强度等不确定因素会对电力系统带来大量的不确定源[2-3]。另外，随着科技的发展，负荷类型也在不断增加，负荷的不确定性也应该引起重视[4]。大量不确定源的引入，导致传统的潮流分析方法不能够有效地分析、评估电力系统当前的运行状态和所面临的运行风险。概率潮流（probabilistic power flow，PPF）考虑了输入变量的概率特性，求取潮流输出变量的概率信息，能够有效地分析不确定源给电力系统运行带来的影响[5]。

概率潮流分析中，对不确定源的概率建模有2个步骤：边缘分布建模和相关性建模。边缘分布建模是用特定分布类型和特定分布参数来描述单个随机变量概率特性的过程，需要根据实测样本，通过数理统计的方法来实现。常用的不确定源的物理对象和所用分布类型有：用韦布尔分布（Weibull distribution）描述风速的不确定性，正态分布（Normal distribution）描述负荷的波动规律等[4,6]。相关性建模是对2个随机变量的不确定性之间关联程度的刻画，常用皮尔森相关系数来进行表征[7]。文献[7]认为在实际应用中，随机变量之间的相关性必须予以考虑，优秀的概率方法必须具备处理随机变量相关性的能力。

由于实际场景中不确定源种类多样，所涉及的边缘分布模型复杂，概率潮流分析时难以直接基于随机变量概率模型产生计算样本。对于这个问题，文献[8]采用Nataf变换，建立了原始分布域与标准正态分布域之间的转换关系，使样本得以在标准正态分布域进行生成。该方法的关键在于求解标准正态分布域变量的相关系数。对于标准正态分布域相关系数的计算方法，文献[9]给出了基于数值积分和二分法的求取方法，其计算过程较为繁琐，耗时可以占到整个概率潮流分析总耗时的一半以上。文献[10]给出了经验公式来快速且精确地实现相关系数的计算，但是所涉及的分布类型极为有限。由于电力系统规模庞大，不确定源种类繁多，随机变量服从的分布类型多样，这些经验公式已经不能满足实际需求。

对于这样的问题，本文采用拉格朗日插值法对原始域变量累积分布函数的反函数进行近似，使用简化牛顿法对标准正态分布域相关系数进行求解，在保证计算精度的情况下，能够提高标准正态分布域相关系数的计算效率。

1 基本模型

1.1 概率潮流模型

对于纯交流电力系统，概率潮流的确定性模型的潮流方程可描述为：

式中：Uia和Uia分别为节点ia和节点ja的电压幅值；Pia和Qia为节点ia上的注入有功功率和注入无功功率；Nb为系统节点个数；Giaja和Biaja分别为系统导纳矩阵第ia行第ja列元素的实部和虚部；θiaja为节点ia与节点ja电压的相位差。

考虑到新能源的接入，在实际计算中，确定性模型还需要嵌入从一次能源变量到对应电厂发电功率的转换。本文考虑了风电场的并网，所使用的风速−风电转换公式为[11]：

式中：vwind表示风速，m/s；PT表示单台风机出力，MW；每台风机消耗无功功率为恒定值0.0002 MV·A。

联合公式（1）和公式（2），确定性潮流模型的输入可以包含：可再生能源电厂的一次能源数据如风速，PV节点发电机的有功出力和电压幅值，所有节点的有功、无功负荷；对于概率潮流分析，本文将电力系统中的随机变量视为输入，确定性模型的其余输入变量均为常数，整个概率潮流的输入变量用X表示；对于输出变量，概率潮流的输出可以包含PQ节点电压幅值与相角，PV节点电压相角，发电机无功出力和支路潮流等；所有输出用Y表示。对于概率潮流分析，基于公式（1）和公式（2），确定性模型可简化表示为：

1.2 随机变量边缘分布模型

对于电力系统中的随机变量，风速用韦布尔分布（Weibull distribution）来建模，而负荷的波动用正态分布来描述（Normal distribution）。本文在只考虑风电厂接入和负荷随机波动的情况下，所使用的边缘分布模型如表1所示。另外，为了验证本文所提出的相关系数计算法，也会用到表2所示概率分布。

表1 概率潮流中随机变量的边缘分布模型Table 1 Marginal distribution model of random variables in PPF calculation

表2 用以验证本文方法的其他概率分布Table 2 Other probability distributions to verify the effectiveness of the proposed method

1.3 随机变量线性相关性模型

本文以皮尔森相关系数作为描述随机变量之间相关性的指标。对于第i个和第j个随机变量Xi和Xj，已知其均值与标准差分别为μi，μj，σi和σj；另外，2个变量之积的均值为μij，Xi和Xj的相关系数ρXij可通过如下方式计算：

对于皮尔森相关系数，变量进行单调非线性变换（如Nataf变换）前后，变量之间的皮尔森相关系数数值会发生变化。在概率潮流分析中，Nataf变换基于标准正态分布变量生成用以概率潮流计算的样本，而标准正态分布样本的生成依赖于标准正态分布变量之间的相关系数，因此需要对标准正态分布域相关系数进行精确计算。

2 概率方法基本理论

2.1 Nataf变换

在概率潮流分析中，具有特定相关性的任意非正态分布样本无法直接生成，需要借助于Nataf变换。Nataf变换采用等概率原理，建立原始分布域变量与标准正态分布域变量的转换关系。已知m维原始域随机 变 量X，即X=[X1,···,Xi,···,Xm]，原始域相关系数矩阵CX，其中第i行第j列元素表示变量Xi和Xj之间的相关系数，记为ρXi j。

设在标准正态分布域，有同等维度的标准正态随机变量Z。第i个随机变量Xi和Zi，满足关系：

对于单峰的非正态分布，连续性随机变量的累积分布函数的反函数是单调增函数，同时Φ是严格单调递增的函数，那么公式（5）所表述的变换过程一定是非线性的单调变换的过程。因此，在标准正态分布域和原始域对应的相关系数数值不同，若要生成用以概率潮流分析的样本，需要首先计算出标准正态分布域的相关系数。根据公式（4）对皮尔森相关系数的定义和概率论的基本知识，原始域随机变量Xi和Xj之间的相关系数和标准正态分布变量Zi和Zj之间的相关系数ρZi j满足如下关系：

通过线性变换可以建立独立标准正态分布变量U和相关的标准正态分布变量Z之间的关系：

式中：L为下三角矩阵，可以通过对矩阵CZ进行Cholesky下三角分解得到，即CZ=LLT，同时可以得到：

基于以上理论，生成独立的标准正态分布样本后，使用式(5)—(8)可以生成原始域变量X的样本，且这些样本满足相关系数矩阵CX。显然，这个过程涉及到使用式(6)或式(8)求解标准正态分布域的相关系数矩阵CZ。而式(6)或式(8)都是含有二重积分的非线性隐式方程。传统的基于数值积分和二分法的求解方法能够较为精确地对ρZi j进行求解，但是耗时及其严重，一般不能满足实时计算的需求。因此有必要对其求解方法加以改进，在保证较高精度的情况下快速完成相关系数的求解，从而加快概率潮流分析的效率。

2.2 基于拉格朗日插值法和简化牛顿法的标准正态分布域相关系数计算法

拉格朗日插值法通过用多项式函数，连续穿过所给的离散点，来近似输入与输出之间的函数关系。对于n+1个给定样本点(x0,y0),···,(xς,yς),···,(xn,yn)，其中所有的x互不相同。可通过式(9)来近似得到从x到y之间的关系y≈L(x)：

式中lς(x)为插值基函数，其计算方法为

通过式(9)和式(10)可知，拉格朗日函数L(x)总能写为

式中a0,a1,···,an均为多项式系数。现使用n阶拉格朗日插值法（阶数为样本点数−1），使用式(11)的形式分别近似式(6)中zi，zj和2个反函数的关系：

式中A0,A1, ···,An和B0,B1,···,Bn均为多项式系数。联合式(8)和式(12)，式(8)中分子的积分项为

其中C表示组合数。式(13)中的积分满足：

其中“!!”表示双阶乘。于是式(13)变为

式中：p+k和q−k为偶数。将式(15)带入式(8)，式(8)可化为不含积分，仅含求和的表达式，简化表示为：

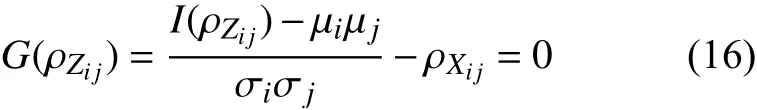
式(6)表明对ρZi j的求解是解一元非线性方程的问题。根据实验，设定收敛精度后，以ρXi j为迭代初始值，G(ρZi j)的导数值恒定为1，使用简化牛顿法，通过若干次迭代便能够对式（16）精确求解。

在实际应用中，对任意2个变量之间的相关系数均实施上述过程，最终可得到标准正态分布域的相关系数矩阵CZ。另外，相关系数矩阵为实对称矩阵，且主对角线元素为1。因此在含有m个随机变量的情况下，需要计算的相关系数个数为0.5m(m−1)，即只需计算矩阵上三角（或下三角）除主对角线以外的元素。最后，此方法是基于拉格朗日插值法和简化牛顿法的求解法（Lagrange interpolation and simplified Newton method，LISNM），在后文中用LISNM表示。本文所提到的改进Nataf变换，即使用LISNM计算标准正态分布域相关系数的Nataf变换方法。

2.3 基于改进Nataf变换的PPF计算方法

在Nataf变换的过程中，LISNM可以对标准正态分布域的相关系数进行精确而快速的计算，从而提高整个概率潮流计算的效率。需要注意的是，Nataf变换用于产生具有特定相关性的原始域样本，而不受到特定概率潮流计算方法的限制，如文献[8,12-13]在概率潮流中对Nataf变换的使用。

在实际应用中，基于改进Nataf变换的概率潮流计算方法可以参照如下步骤：

步骤1：确定电力系统中的不确定源，即随机变量X，并通过数理统计的方法得到其边缘分布和相关系数矩阵CX。

步骤2：反复使用LISNM得到标准正态分布域的相关系数，最终得到标准正态分布域相关系数矩阵CZ。

步骤3：基于特定的概率潮流方法，生成独立的标准正态分布样本，进一步使用公式（7）得到具有相关性的标准正态分布样本。

步骤4：使用公式（5），将所有标准正态分布样本转换回原始分布域。

步骤5：将所有原始分布域的样本，代入确定性模型（3）进行计算，得到相同数量的输出样本。

步骤6：对于输出样本，基于所用的概率潮流方法的理论，得到输出变量的概率信息。

3 算例分析

3.1 LISNM的性能测试

使用表1和表2中的分布类型对LISNM的性能进行测试。设这4类分布的具体信息为：韦布尔分布，形状参数和尺度参数分别为3和10；正态分布，均值和标准差分别为10和1；均匀分布，下界和上界分别为5和15；对数正态分布，对数均值和对数标准差分别为3和0.04。为了充分表明所提方法的适用性，设原始域相关系数数值R，R=[−0.95,−0.9,−0.8,−0.7,−0.6,−0.5,−0.4,−0.3,−0.2,−0.1,0,0.1,0.2,0.3,0.4,0.5,0.6,0.7,0.8,0.9,0.95]。对于R中所有数值，任意2个分布之间、每个分布自身之间都将对其进行计算。

使用高精度的基于辛普森数值积分法和二分法的相关系数求解法作为精度参考（Simpson’s method and bisection method, SMBM），来测试LISNM的精度。其中SMBM的收敛精度设置为10−4，表示在迭代结束时，SMBM的结果与相关系数真实值的绝对误差小于10−4。

定义相关系数的最大绝对误差εmax和平均绝对误差εmean，其计算方法如公式（17）所示：

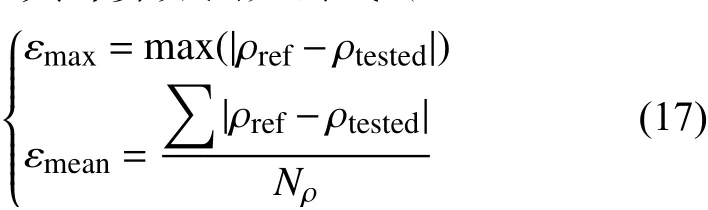
式中：ρref和ρtested分别表示通过SMBM计算得到的相关系数和通过LISNM计算得到的相关系数；Nρ表示相关系数的个数。

对于所设的4类变量之间以及每类变量自身之间，分别使用SMBM和LISNM对R中的所有数值进行计算，得到标准正态分布域的相关系数精度和计算总时间的结果如表3所示。

表3 相关系数计算结果Table 3 Computing results of correlation coefficients

在表3中，LISNM的拉格朗日插值法使用插值点个数为17，简化牛顿法迭代初值与原始域相关系数数值相同，雅可比矩阵为固定值1。根据表3的结果，LISNM的计算时间比SMBM小了3个数量级，计算时间大大减少。而计算精度上，根据SMBM的精度设定，SMBM结果小数点后4位是完全精确的，而LISNM计算得到的结果与SMBM相比，最大误差和平均误差均在10−4的数量级。也就表明本文所提方法的精度至少为10−3，从数值上来看，其结果非常精确。

3.2 基于改进Nataf变换的PPF计算

从3.1节的结果可以看到，LISNM的计算速度快，精度高。设定以下算例，测试LISNM的概率潮流计算精度的影响。概率潮流方法分别为蒙特卡洛仿真法（Monte Carlo simulation method,MCSM）和Hong氏e method,HPEM）[14]。

基于MCSM的方法在样本数足够大时，其计算结果也是依概率收敛于精确的结果。同时由于计算机只能够伪随机生成计算样本，即使样本数量非常大，样本的相关系数矩阵与所给矩阵本身便存在一定误差。通过实验测试，样本足够多时，这个误差的最大值小于10−3。根据3.1节结果可以知道，LISNM计算的相关系数矩阵误差和MCSM随机样本相关系数的天然误差相当。因此，理论上基于MCSM所测得的结果误差应该更大。

但是对于以HPEM为代表的近似法，在独立标准正态分布域采得的样本是固定的。根据公式（7），在实施过程中，每个样本点都会直接受到标准正态分布域相关系数矩阵的影响。并且在算例既定的情况下，其原始域样本数值仅受到相关系数矩阵的影响。因此，HPEM的计算结果对相关系数矩阵的数值非常敏感。相比于MCSM而言，HPEM的潮流结果误差更能体现Nataf变换中相关系数计算精度对概率潮流分析结果精度的影响。

基于标准的IEEE 118节点系统，接入如文献[11]完全相同的风电装置(共14处)。对于所有负荷，其有功负荷均服从正态分布，均值为算例中对应原始值，标准差为均值的5%。另外，在计算中保证负荷的功率因素与原始算例对应负荷的功率因素相同，从而决定无功负荷。其中有功负荷之间的相关系数为0.6，负荷与风速之间相关系数为0.05。另外，本文用相对误差来描述均值与标准差计算结果的精确度，数值越小代表该结果越精确，其具体计算方法如公式（18）所示：

式中：εr表示相对误差；rref和rtested分别代表通过SMBM和LISNM进行相关系数转换后的概率潮流计算结果。根据设定，在使用同一种概率计算方法时，认为基于SMBM的概率分析最终结果是标准结果，考察基于LISNM的概率分析结果与参考结果的偏差（即误差）。

选取网络有功损耗、平衡节点发电机无功出力作为输出。分别使用SMBM和LISNM进行相关系数计算，使用基于100000个简单随机样本的MCSM计算结果的概率密度如图1所示。对于概率密度精确度的衡量，使用文献[15]中定义的指标频率直方图相似度(frequency histogram similarity index,FHSI)来描述2个概率分布的相似程度。当其中一个概率密度作为标准结果时，FHSI的数值可以作为另一概率密度的精度指标。对于FHSI，其数值范围分布在区间[0,1]内，数值越大表明所指结果越精确。根据文献[15]所给判据，当FHSI数值不小于0.9时，认为所指的概率分布是精确的。

图1 基于SMBM和LISNM相关系数计算法的MCSM概率潮流结果Fig.1 PPF results calculated by MCSM based on correlation coefficients obtained by SMBM and LISNM respectively

另外，分别使用MCSM和HPEM计算得到的输出的均值与标准差误差如表4所示。在图1中，2种方法得到的输出概率密度的相似度超过0.98。根据表4中的结果，当使用LISNM计算相关系数，使用MCSM计算概率潮流，最终结果的均值与标准差的误差均不到0.2%。这表明使用LISNM进行相关系数计算，且使用MCSM实现概率潮流分析的结果精度非常高，无论是输出变量的概率分布还是其均值和标准差都能够满足实际应用需求。

表4 基于改进Nataf变换的MCSM和HPEM概率潮流计算误差Table 4 PPF calculation errors of improved Nataf transformation based MCSM and HPEMmethods%

根据前面的分析，HPEM结果的均值与标准差对标准正态分布域的相关系数矩阵元素的数值更加敏感。但是表4的结果表明，LISNM的误差对HPEM的概率潮流计算结果的影响非常小。这一方面说明了LISNM对相关系数计算的精度完全满足概率潮流计算的要求。另一方面，这表明LISNM的误差给概率潮流结果带来的偏差，远远小于基于MCSM的概率潮流计算结果本身的不稳定性。

3.3 改进Nataf变换的必要性和PPF耗时分析

采用SMBM计算标准正态分布域相关系数，且以0.1为收敛精度，记作in-SMBM(inaccurate SMBM)。分别使用100000组简单随机样本的MCSM和HPEM法进行概率潮流计算，其计算结果的误差见表5。

表5 相关系数计算不精确时的概率潮流结果误差Table 5 Calculation error of PPF under inaccurately calculated correlation coefficients%

比较表4与表5中的结果，在相关系数计算不精确的情况下，概率潮流计算输出的误差均有明显增大。其中均值误差虽有增加，但是在数值上可以认为是精确的。但是标准差的误差均超过了9%，相比于表4中的不到0.2%，其误差增大明显，精度已经不能满足实际应用的需求。因此，不精确的标准正态分布域的相关系数将增大概率潮流计算结果的误差，其中输出变量的标准差对相关系数的精度更为敏感。这表明了在概率建模中精确地对标准高斯域相关系数进行计算的必要性。

概率潮流计算所消耗的时间，主要由相关系数计算耗时和概率潮流计算耗时组成。表6给出分别使用LISNM和SMBM法计算相关系数以及分别使用HPEM和MCSM计算概率潮流的耗时情况，并给出了该组合方法完成整个概率潮流分析的总耗时。

根据表6中不同方法下相关系数计算耗时的占比可以发现，相关系数计算的耗时在整个概率潮流分析中是不可忽略的。对于特定的概率方法，计算相关系数的耗时甚至占到整个概率分析耗时的80%以上。

表6 相关系数计算耗时与概率潮流计算耗时的比较Table 6 Comparison of computing time for correlation coefficient calculation and that for PPF calculation

在表6所示的各种PPF方法组合中，相比于SMBM，LISNM对于概率分析效率的提升非常可观。

4 结论

1）本文提出的LISNM能够快速地计算标准正态分布域的相关系数，加快了Nataf变换的实施速度，极大地提高了概率潮流分析的效率。同时，LISNM对相关系数的计算精度高，在提升概率潮流分析效率的同时，保证其结果的精度。

2）基于LISNM的相关系数计算的误差，经概率潮流传递后，对概率潮流计算结果的影响远远小于蒙特卡洛法自身结果的不稳定性。而通过Hong氏点估计法的传递，LISNM的误差对概率潮流结果的影响非常小，这也表明了LISNM的精确性。

3）在电力系统概率潮流分析中，相关系数计算的耗时占比大。提高相关系数计算的效率，可以极大加快整个概率潮流分析的过程。