一道“极值点偏移”试题的解答之旅

郑 良

(安徽省合肥市第四中学 230000)

“极值点偏移”是高考数学的常见问题，但不少师生仍然觉得此类问题解法零碎、解题过程繁琐，对此类问题感到困惑与迷茫.本文简要呈现教学过程中师生对一道“极值点偏移”试题的思考与求解历程，尝试对各种解法进行梳理，以期抛砖引玉.

题目已知函数f(x)=lnx-ax+b(a,b∈R)有两个不同的零点为x1,x2.

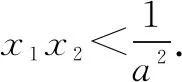
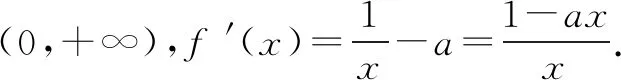
综上所述，a>0，函数f(x)的最大值为-lna-1+b，无最小值.

(2)由(1)可知，函数f(x)有两个不同的零点为x1,x2，则必有a>0(下同).

证法1尝试消去参数a，齐次化消元

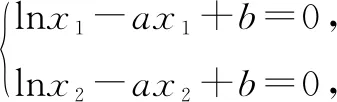
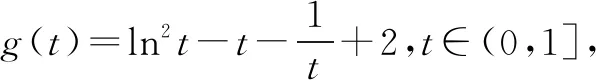
证法2利用对数平均值不等式

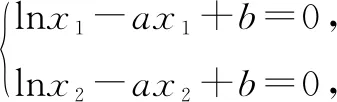
证法3尝试构造对称函数进行转化

多数学生尝试如下：

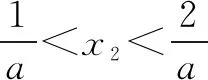
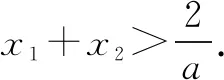
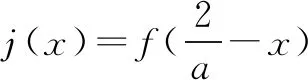
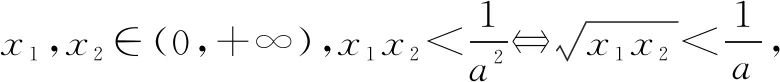
因为函数f(x)=lnx-aelnx+b有两个不同的零点为x1,x2，所以s1=lnx1，s2=lnx2是方程s-aes+b=0的两个根，只需证明s1+s2<-2lna.

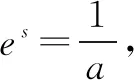
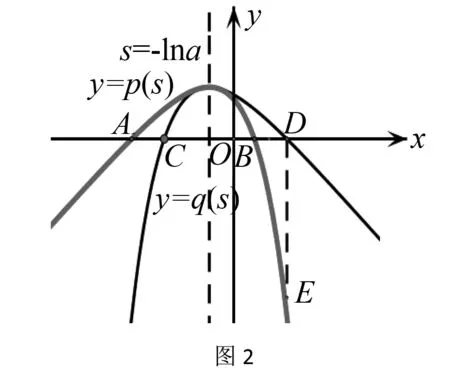
在同一坐标系中，画出函数y=p(s)和y=q(s)的图像，如图2所示.A(s1,0)，B(s2,0)，C(-2lna-s2,0)，D(-2lna-s1,0)，E(-2lna-s1,p(-2lna-s1)).p(s2)=p(s1)=q(-2lna-s1)>p(-2lna-s1)，而s2，-2lna-s1∈(-lna,+∞)，而函数p(s)在(-lna,+∞)上单调递减，得s2<-2lna-s1，所以s2+s1<-2lna.