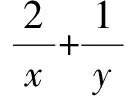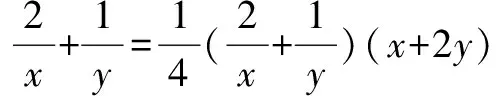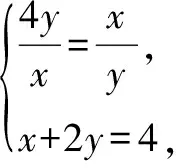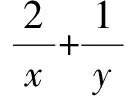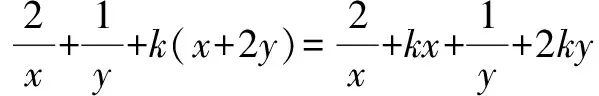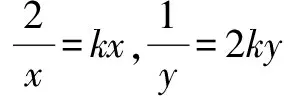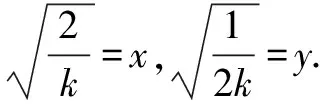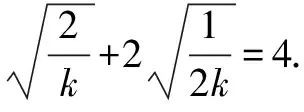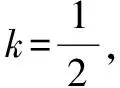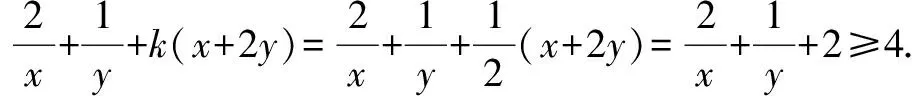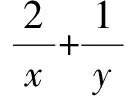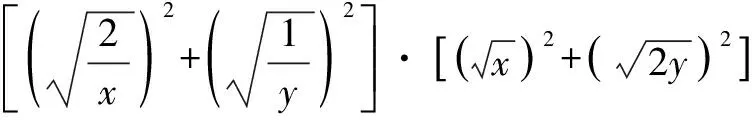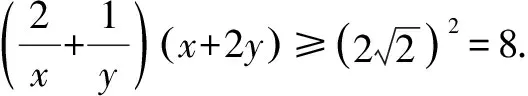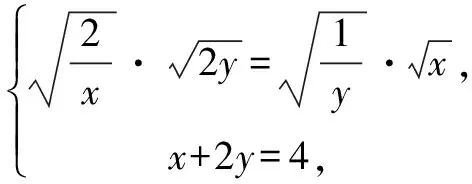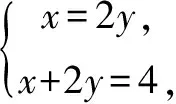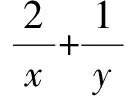横看成岭侧成峰 一题多解妙无穷——一道最值问题的解法探究

刘稳殿

(陕西省白河县高级中学 725899)

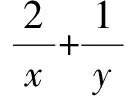
此题解法较多，作者总结了基本的五种求解方法，供读者参考，不足之处，敬请指正.

解法1 (代入消元)回归基础，适用于已知二元关系，用一元表示另一元的情况.

由x+2y=4,得x=4-2y.

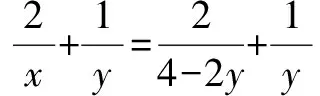
因为x,y为正数，且x+2y=4，所以0

解法2 (常数代换) 回归问题本质，适用于二元均为正数且和为常数的求最值问题.

因为x,y为正数，且x+2y=4，

解法3 (利用基本不等式)直接求解，适用于两分式相加，分子(分母)为已知常数.

因为x,y为正数，且x+2y=4，

即0

解法4 (待定系数)引入参数巧变形，将二元关系整体化.(注意x+2y=4为一个整体，可引入一个参数k，k>0)

设k>0,由x+2y=4，得k(x+2y)=4k.

解法5 (利用柯西不等式)，通过拆项重组或添项等方法构造符合柯西不等式的形式及条件.

因为x>0.y>0,x+2y=4，