地球构造动力的合力强度方程建立
李务伦,李相通
(1.吉林省煤田地质局二〇三勘探队,吉林 四平 136000;2.黑龙江省林业设计研究院,黑龙江 哈尔滨 150001)
地球内部存在自身引力场,不停地自转,同时还处在外部引力场之中,内部的热运动形成热结构,热结构中存在浮力强度,这些构成了地球的构造动力。对目前地球已发现的地球构造周期性、地球韵律[1]等,可用这一构造动力进行解释,下面从地球内部引力场开始,逐一讨论。
1 地球为球态的原因及内部合力强度方程
地球是球态,月亮是球态,所有星球都是球态。宇航员在太空中将相当量的液体从储液盒中挤出,若在地面将摊成薄薄一层,而在太空,由开始的不规则,经不太长时间后,就变成球态。这是为什么呢?要回答这一个问题离不开万有引力定律。
1.1 均匀球体内外引力强度
万有引力定律表达式为

式中:G为万有引力常数;m1和m2为物体质量;r为m1和m2两物体质心之间距离;F为引力,引力方向在m1和m2两物体质心的连线上。
根据式(1),对于任意质量为m的质点,在距离为r的一点P所产生的引力场强度[2](或简称引力场,即一单位质点在P点所受引力)为

式中:G为万有引力常数;负号表示吸引力方向。
1)球外引力强度计算。图1中,实心均质球外一点P的引力强度可以通过以下步骤求出。设球半径为R且均质,密度为ρ,质量为M,OO1=y,图示球外P点距球心距离为r。圆平面O1垂直y轴,与平行于圆平面O1的另一圆平面相距dy,平行于z轴的AO1B,O1A=O1B=k,相同质量质点A和B在P点的引力强度分别为dE'和dE,方向见图1。
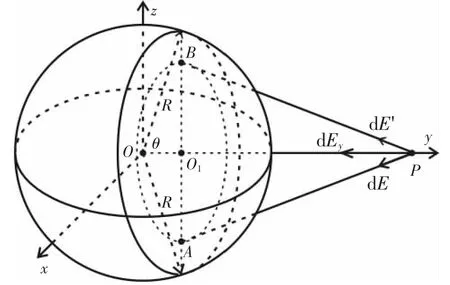
图1 均匀球体外引力强度示意图
对称的A和B两点在平行z轴方向上合引力强度为0,所以半径为k的圆在P点平行平面xOz的引力强度为0,圆平面O1内,A点或B点对P点平行y轴的引力强度为
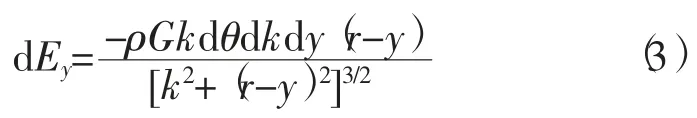
圆平面O1内半径为k的圆环在P点平行y轴的引力强度为
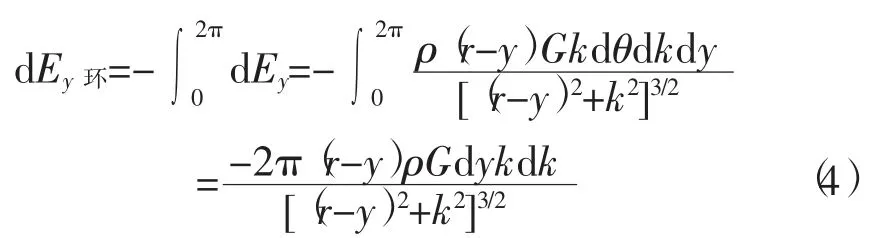
圆平面O1在P点平行y轴的引力强度为

球O在P点平行y轴的引力强度为
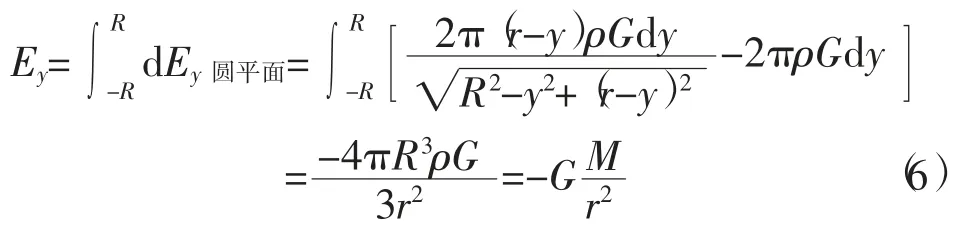
由于球的对称性,所以球外任意方向一点P,根据Ey又可写为
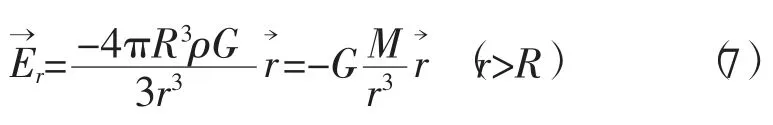
高斯定理:引力场中引力通量用Φ表示,高斯定理可表述为:通过一闭合曲面的引力通量等于该曲面所包围的所有物质质量代数和的-4πG倍,即

2)球内引力强度计算。图1的球内部任意一点的引力强度,既可积分方法求出,也可根据高斯定理得出。球内任意一点到球心距离为r的引力强度为
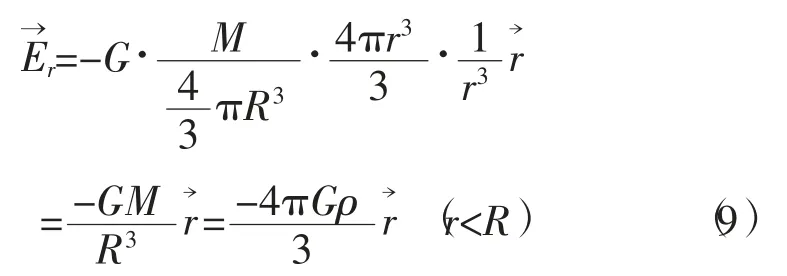
3)球体内的引力位。图1中,球外任一点P距球心距离为r的引力位V,可由式(7)积分得出,根据场论推知为
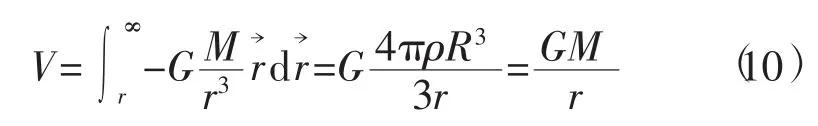
半径为R的球内部引力位,可由式(7)和式(9)积分得出,根据场论推知为
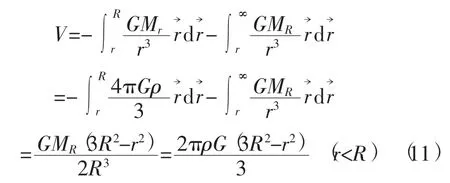
4)球体内的压力。图2中的均匀球体,密度为ρ,半径为R。球内压力可根据式(9)计算,计算过程为:在图2半径为r的球上任取一微元ds,微元的高度为dr,因此体积为dv=dsdr,微体积的质量dm=dvρ,一单位质点为将其带入式(9),于是有
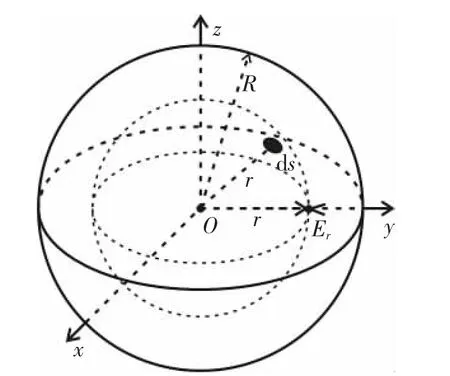
图2 均匀球体内压力计算示意图
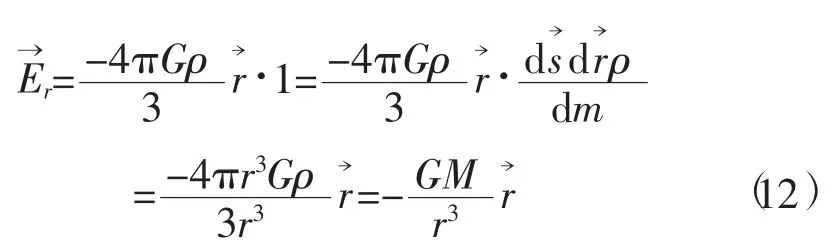
上式两边同乘dm后得
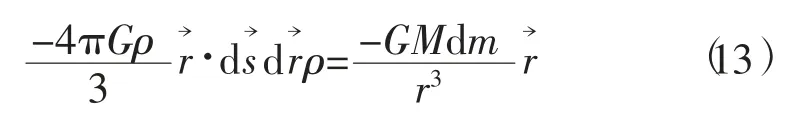
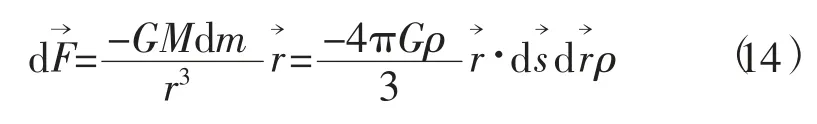
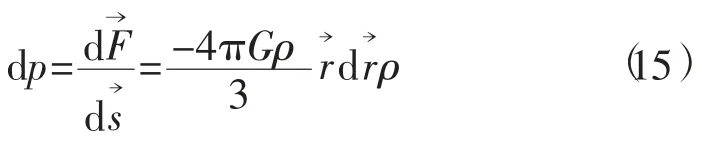
根据力的可加性,对上式从r到R积分,于是得到

5)引力强度线方程及引力场性质。根据矢量线所满足的微分方程[3]15
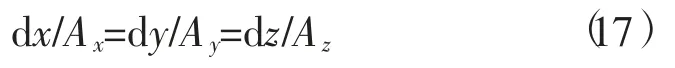
式(7)和式(9)的引力线方程为

从上式得出,因为引力线均为经过球心的直线方程,所以所有引力线均垂直于半径为r的球面;而等引力强度面也为同样的球形,所以其等引力强度面方程为

式(18)与式(19)的关系可用第42页图3表示。根据上面的分析,球内压力由式(9)求出,所以压力方向线方程也为式(18),等压力面方程为式(19);另引力位方程由式(7)和式(9)求出,所以等引力位面方程也为式(19)。
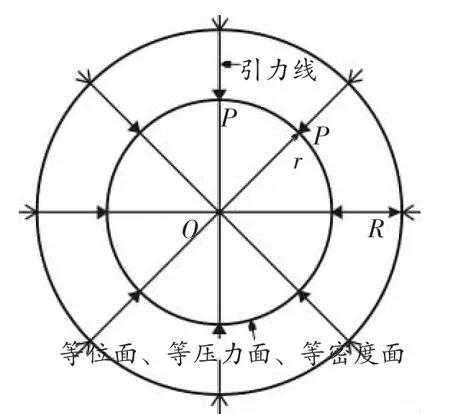
图3 引力位引力线剖面图
根据上述叙述可得出单一物质形成的球内具有以下性质:一是引力线为直线、引力线方向与压力方向均指向球心;二是等引力强度面、等压力面、等引力位面均为球形;三是引力线与等引力强度面、等压力面、等引力位面垂直;四是球内部球面上,引力强度值处处相等,压力值处处相等,引力位值处处相等;五是球内任一点的各向应力值与该点的压力值相等;对于均匀小密度在外的球层,以上性质也同样存在,即这些性质依然成立;六是所有物质,由球心向外,按密度从大到小圈层展布。这些性质决定了太空中液体很快收缩为球形,推而广之,星体为球态的原因也源于此。
1.2 均匀旋转球体内合力强度
图4中的球为均质刚性,旋转角速度为ω。A为球内任意一点,距球心距离为r,该点的引力强度为式(8),A点处单位质点向心力为
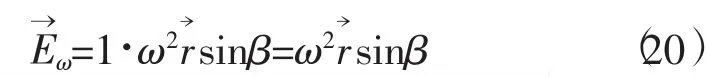

图4 旋转球体合力强度计算示意图
单位质点向心力,也可以看作是向心力强度,这样就与引力强度统一起来了,进而可以将它们投影到图示的坐标轴上,表达式分别为
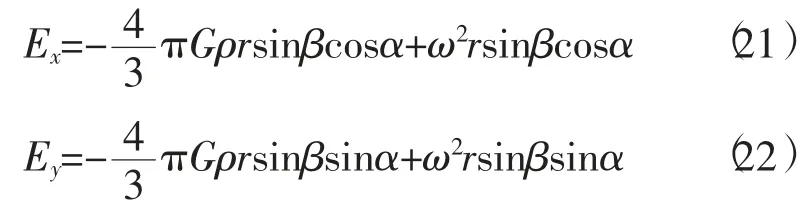

所以引力强度、向心力强度之合力强度为
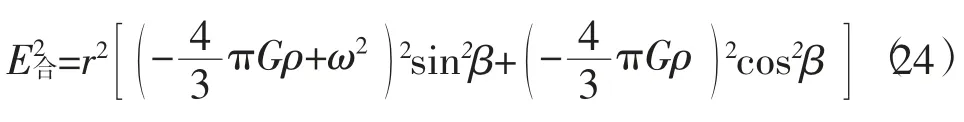
椭球为
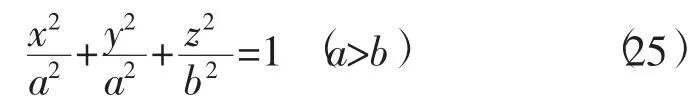
的极坐标方程为
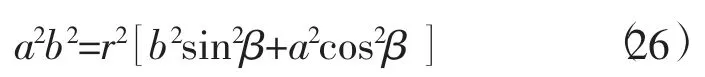
对比式(24)和式(26)可以发现,合力强度方程即式(24)也为椭球方程。如果图3中的球不具刚性,内部质点将依合力强度方程式(24)运移,最后变为椭球形,因此地球为椭球形。根据方程式(21)、式(22)、式(23)也可求出类似式(18)的强度线方程,以及由式(24)求出等压力面和等位面方程,只不过这些方程的球形复杂,而且与要解决的问题关系不大,因此对这些不做详细讨论,以后也如此。
为了使式(24)更具有一般性和普遍性,将具有密度ρ=ρ(r)(r<R)随半径变化,这时球内引力强度为

将式(27)替换式(24)中的均匀介质引力强度得
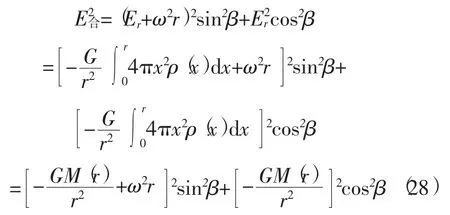
地球在赤道引力强度与向心力强度之比为
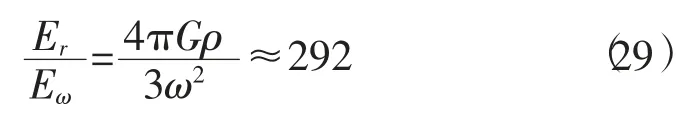
如此小的向心力强度使得地球变为椭球形。
1.3 外力场对旋转球体内合力强度的影响
地球处于太阳系中,太阳系位于银河系猎户旋臂上,月亮是离地球最近的星体。因此地球处在其他星球形成的合引力场中。根据月球与地球相对位置的不同,引力强度有远、近和平均之分,其值分别为E远=2.981 17×10-5N,E近=3.713 84×10-5N,E平=3.317 27×10-5N。如此小的引力强度引起潮起潮落及固体潮。
太阳的质量占太阳系质量的98%,下面忽略其他行星的作用,只算太阳在地球处的引力强度。同样太阳与地球相对位置有远、近和平均之分,其值分别为E远=5.734 9×10-3N,E近=6.131 8×10-3N,E平=5.928 2×10-3N。太阳系距银心2.6万光年,银河系质量为4.177 1×1041kg(目前有的认为银河系质量为5.967 3×1042kg),九成质量位于银盘上。
很难推出从太阳到银河系中心所有物质形成的引力强度在太阳处合引力强度公式,但可根据“一均匀球体或均匀球层在其外一点所产生的引力强度等于将其全部质量集中于球心所产生的引力强度”和高斯定理可粗估其强度。根据高斯定理,2.6万光年以外的物质对太阳系的引力强度为0。2.6万光年以内物质保守估计不应少于银河系总质量的1/4,即约1041kg(或1042kg)。因此可粗估引力强度为E银=1.1×10-4N(或1.1×10-3N)。根据月球在地球处产生的引力强度两引力线与地球相切的最大夹角不足2°,可以认为这三者在地球处引力线是平行线,合引力强度引力线也平行(见图5),因此可设在地球处存在的地外合引力强度为Ew,其方程为
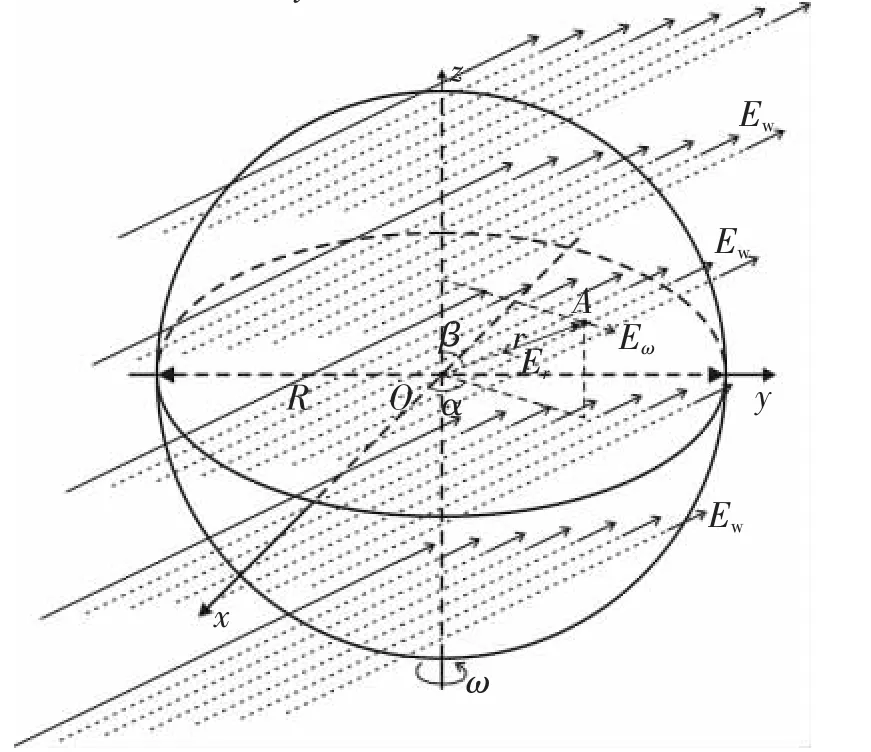
图5 周期性变化力场中旋转球体

式中:t为时间;r为球内质点距球心距离;σ为与z轴夹角;τ为在xOy平面内与x轴夹角。
在图5的A点,球自身、自转、Ew合力的各分量为
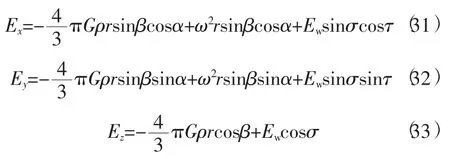
合强度为
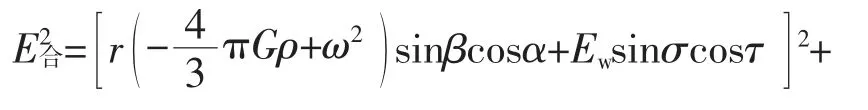
一般情况下,将式(27)替换式(34)中均匀介质引力强度得

月球在地球的引力强度量级前面已叙述,如此小的量级则引起地球引力潮,太阳和银河系的引力量级也会在构造中留有痕迹。同时根据式(34)可以得出球内性质:球内所有质点具有动态平衡和周期性变化的特点。而对于前面球内性质,根据式(34)可改写为:一是合力强度线为曲线、合力强度线切线方向与压力方向相同,所有合力强度线止于球心;二是等合力强度面、等压力面、等合力位面均为椭球形;三是合力强度线与等合力强度面、等压力面、等合力位面相互垂直;四是球内部椭球面上,合力强度值处处相等,压力值处处相等,合力位值处处相等;五是球内任一点的各向应力值与该点的压力值相等;六是所有物质由球心向外按密度从大到小圈层展布。
1.4 合力强度方程成立证据
太阳系绕银心一周约2.5 Ga,8次穿越银道面,穿越银道面时间间隔是30~35 Ma左右。在地球穿越银道面时,陨击撞击地球,与地球穿越银道面时间相合[4];还有学者对地质事件与穿越银道面做了研究,研究表明地球各圈层主要地质事件的旋回周期见第44页表1和表2[1]35-36。从表1和表2不难发现,银河系对地球的引力强度影响了地球的方方面面。地球地壳的韵律分级见第45页表3。从表3更能看出地外引力强度对地球的作用;地球存在经向和纬向构造带,以及54种朝东定向的构造现象[1]42-43,它们是地球自转导致的,因此可以断定式(34)或式(35)是成立的。
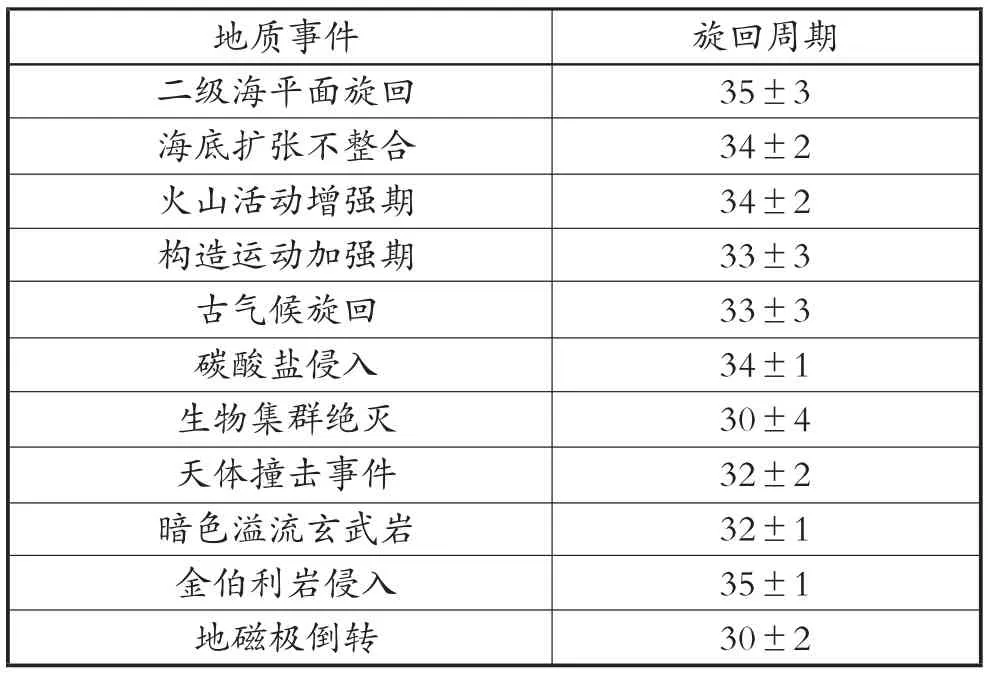
表1 地球各圈层主要地质事件的旋回 (Ma)
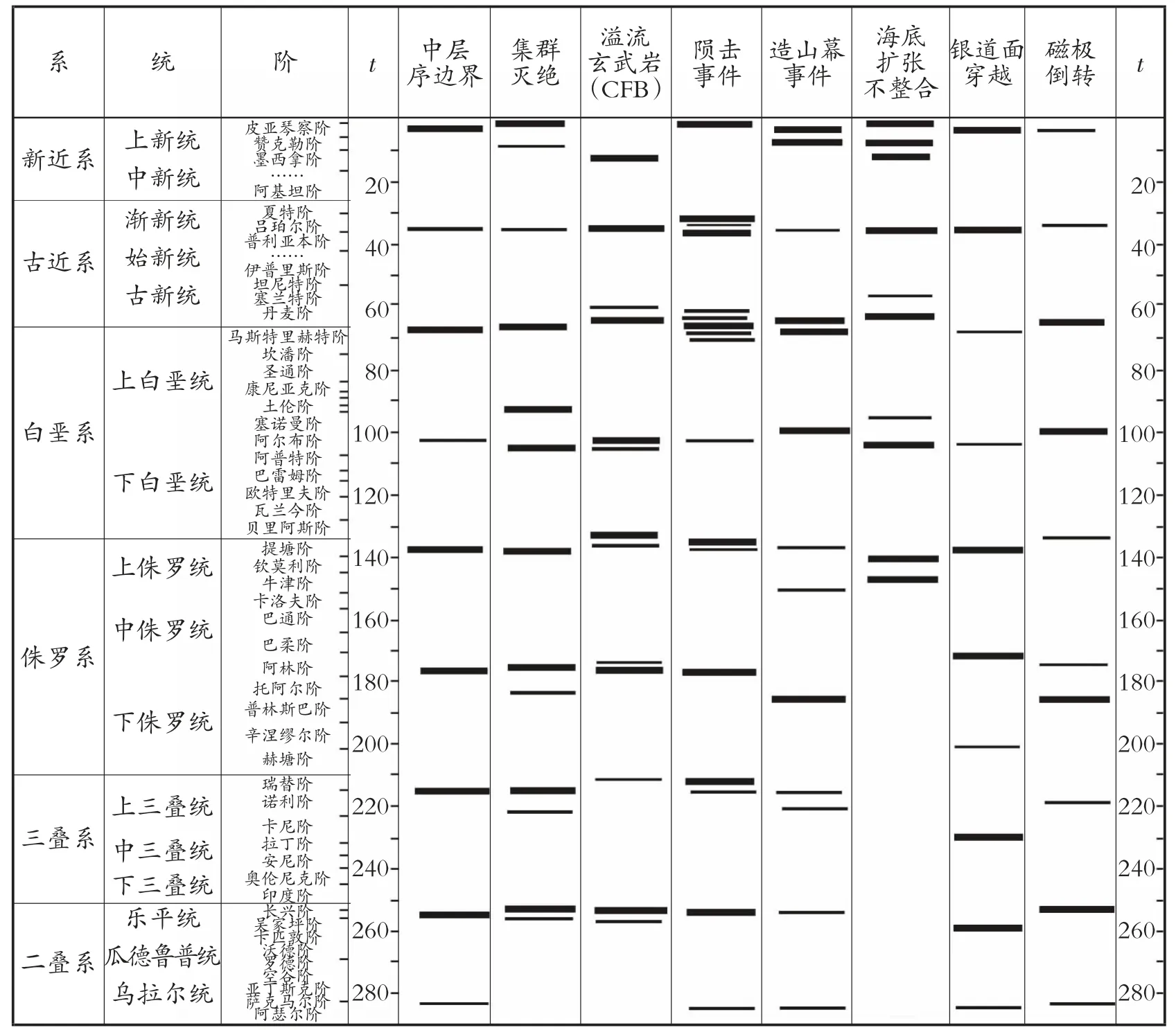
表2 地史上35 Ma左右的重要地质事件集中期与穿越银道面时间对比 (Ma)

表3 地球的韵律分级
2 物体的浮沉
第45页图6为浮沉剖面示意图。图6-a中,左侧长方体在外力F作用下侵于液体中,其上作用力F=V(ρ2-ρ1)E,式中E为引力场强度,V为长方体体积。
当图示该力不存在时,此时的-F为长方体向上的运动力即浮力,而长方体质量为m=Vρ1,那么单位质量的浮力为

图6-b中,当去掉长方体的外力F时,长方体将向上运动,即上浮。E浮的存在引起长方体上部压强的增加量Δp>0和质量的相对增多,图中的等压力线L1因此有水平如钟形上展,变为图示的L1。长方体的上升,长方体底面对接触底面的液体因E浮的存在引起长方体底部压强的增加量Δp<0和物质量相对减少,使得图示的等压力线L2有水平如钟形下延为L2。长方体上部物质将如图示的方向运动,而长方体周边物质在黏滞力的作用下如图示向上运移,从而形成图示的流体旋转。
图6-a中的右侧长方体,去掉上提力F后将下沉,运动情况与上浮相反,见图6-c。沉力强度为
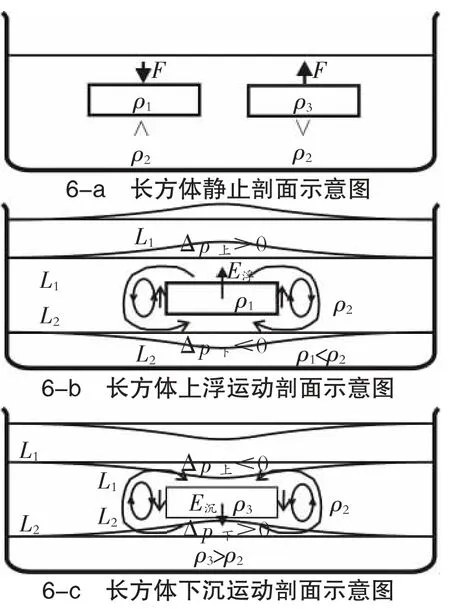
图6 浮沉剖面示意图
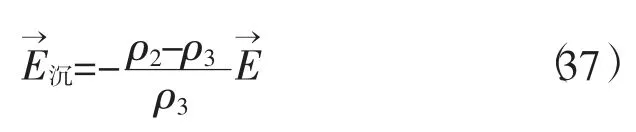
根据Talwani等1965年对横切大西洋洋中脊北部的重力异常与海底形态的研究成果,得到重力剖面图,见第45页图7。
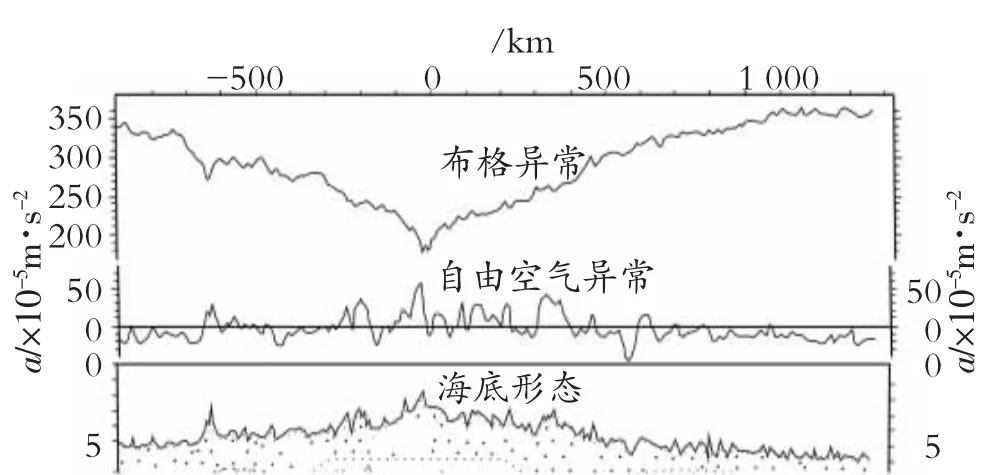
图7 重力剖面图
图7中自由空气异常极小,表明洋中脊为均衡,但中部对应洋中脊形态,由洋中脊最高处向两侧,自由空气异常还是由大向小变化的趋势,说明物质有富余;布格异常是负的,表明洋中脊下面质量短缺,这成了一对矛盾[2]。大洋中脊为海底扩张的地方,热的物质上涌而使海底扩张形成,因而具有物体上浮的特征,反映在等压力面上就具有图6-b的形态,这种形态正是洋中脊存在质量既富余又短缺的情况,这样质量富余和短缺的矛盾得以解决。
3 热结构中合力强度方程建立
地球于星云中吸积而成,聚首的星云物质存在力、化学势、物质展布的3种不平衡,物质并非严格依照式(18)和式(19)排列,也非时下的地球具有圈层。以往的研究认为,重组和运移是在热结构中进行的[5-8],热结构见图8。物质的重组和运移一分为三,小密度物分异后到热结构图8的左右上角,大密度物聚于加热结构的底部。
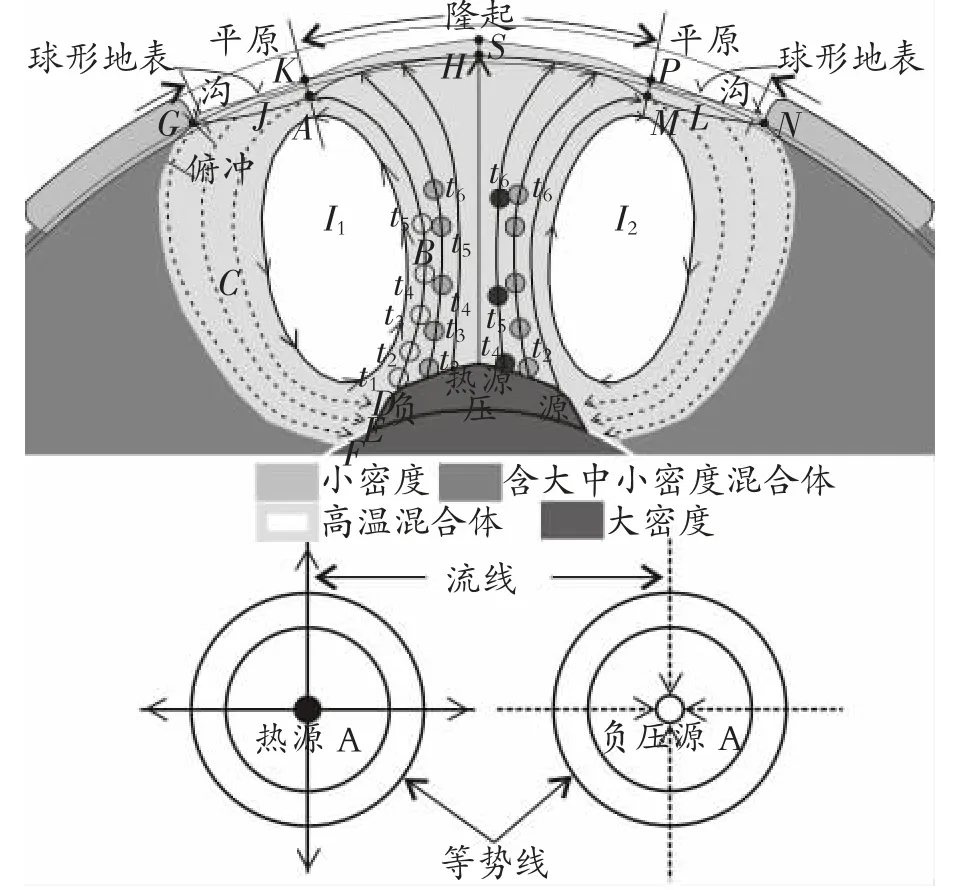
图8 热运动流线剖面及投影示意图
星云物质聚集后,因引力位能而生热,热使得物质重组迁移,并使粒子间距离增大,从而使得物质上浮,同时使得其内部大比重粒子下沉聚集,这其中就包括放射性重元素U,Tu等,这样位能转为热能和衰变热(链式核裂变热)[9]形成上部的热源供给地,上部物质持续上升,到最高后返回到出发地,热结构形成(见图8)。对上部供热,是热源;热源促进热结构中粒子上升,在热结构底部形成负压,因为是源,就符合拉普拉斯方程Δu=0,因此就有了图8下部热源、负压源。
中间上升部位因与周边存在密度差,所以存在式(36)的浮力强度。设该浮力强度位于在图4中的A点,浮力强度与z轴夹角为λ,在xOy平面内与x轴夹角为μ,因此浮力强度在各轴的分量为
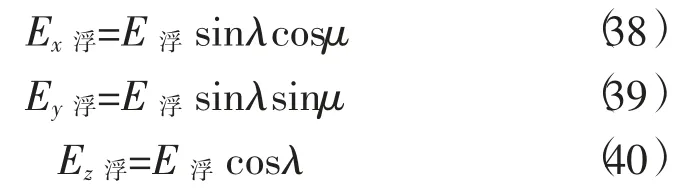
将上述三式与式(31)、式(32)、式(33)对应相加,其A点合强度为

一般情况下,球内引力强度换成式(27)得

负压是由上浮形成的,因此负压也存在强度,它等于-E浮。图8中的物质上升到最高点时,开始向四周运动并降温,在沟处回返,形成俯冲。因此在俯冲带内存在下沉和负压,所以在图4中A点,沉力强度与z轴夹角为θ,在xOy平面内与x轴夹角为δ,因此沉力强度在各轴的分量为
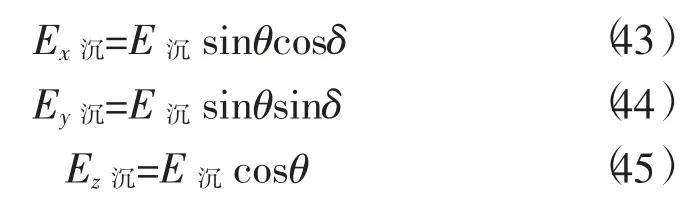
设在图中A点,负力强度与z轴夹角为γ,在xOy平面内与x轴夹角为φ,因此负力强度在各轴的分量为

从式(43)到式(48),与式(31)、式(32)、式(33)对应相加,A点强度为
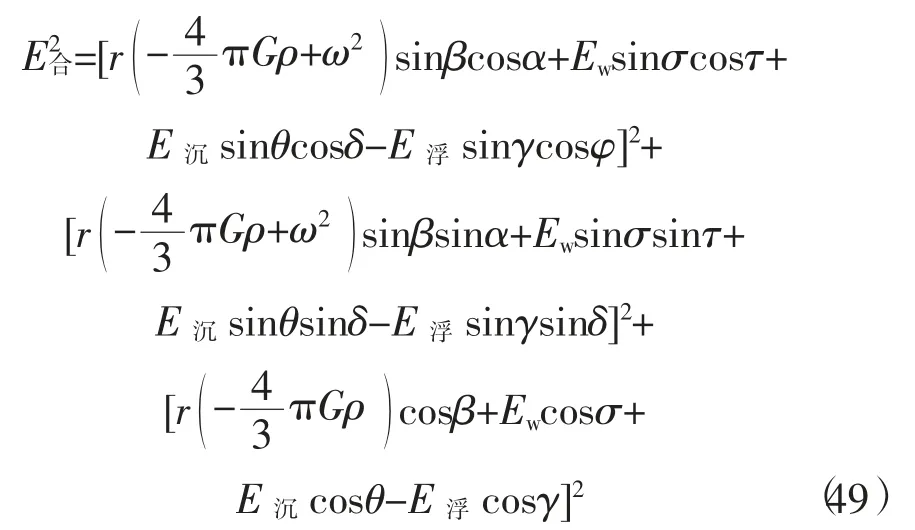
一般情况下,球内引力强度换成式(27),得
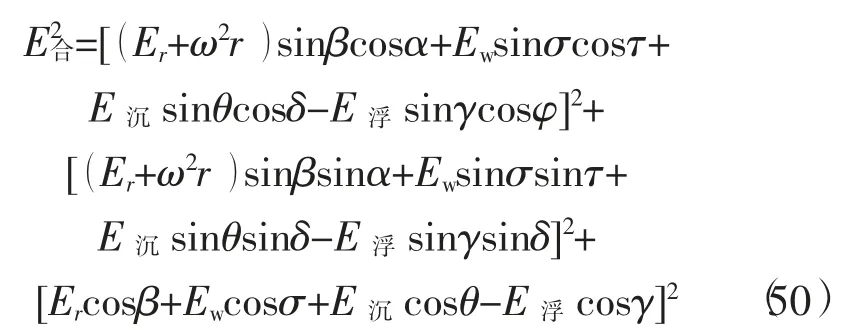
式(41)、式(42)、式(49)、式(50)均为椭球方程,是多因素方程。
4 小密度物与热结构间的平衡分析
图9为小密度物在俯冲处受力示意图,是图8左上的一部分。
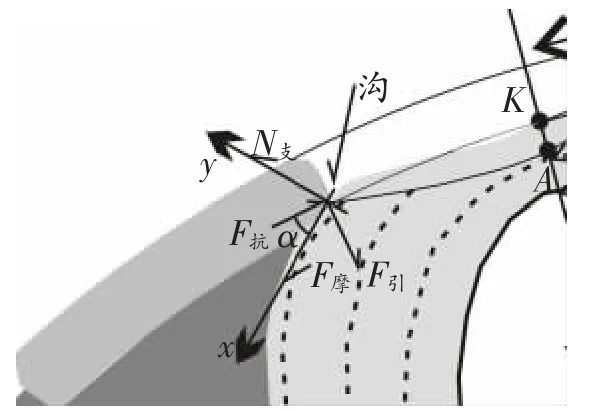
图9 小密度物在俯冲处受力示意图
小密度物右下与热结构接触处,对小密度物的任意一质点,存在图9所示的受力:热结构对小密度物的支撑力N支,热结构对小密度物摩擦力F摩,摩擦力使得左侧小密度物产生图9所示的反抗力F抗,及上覆小密度物对该质点重力F引。在图示的坐标系中F抗与x轴,F引与y轴夹角均为α。在x轴、y轴的合力分别为
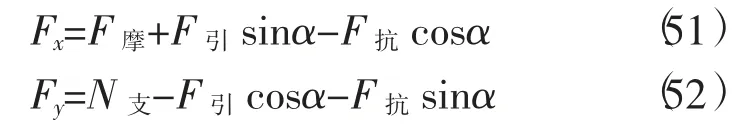
当Fx=0时,沟的位置稳定;Fx>0时,沟的位置向图示左下移,反映热结构扩大,小密度物漂移或消减;Fx<0时,沟的位置向图示右上移,反映热结构减弱,沟后退。正是由于式(41)、式(42)、式(49)、式(50)、式(51)、式(52)这些方程的存在,因此使得地球构造具有多样性。
5 热结构存在验证
帕皮提是一火山岛,离汤加弧不远,可以先假定其下存在图8式的点源热结构。用测线验证是否存在图8的海底地形,见第47页图10。
图10-a是谷歌地球在帕皮提和汤加弧间的截图。图中Ⅰ为帕皮提到海沟一条测线,在测线上等距离连续取得海底高程,并对应做出海底测线地形图。在海底测线地形图上,除A处存在凸起外,其他处虽有波动,但不及A处,对这一测点线,作手工拟合,见图10。从手工拟合线上可以看出:帕皮提到海沟的海底地形,基本上与图8中S点到G点的地形相同。测线Ⅱ、测线Ⅲ和测线Ⅰ基本相同,可见存在热结构。
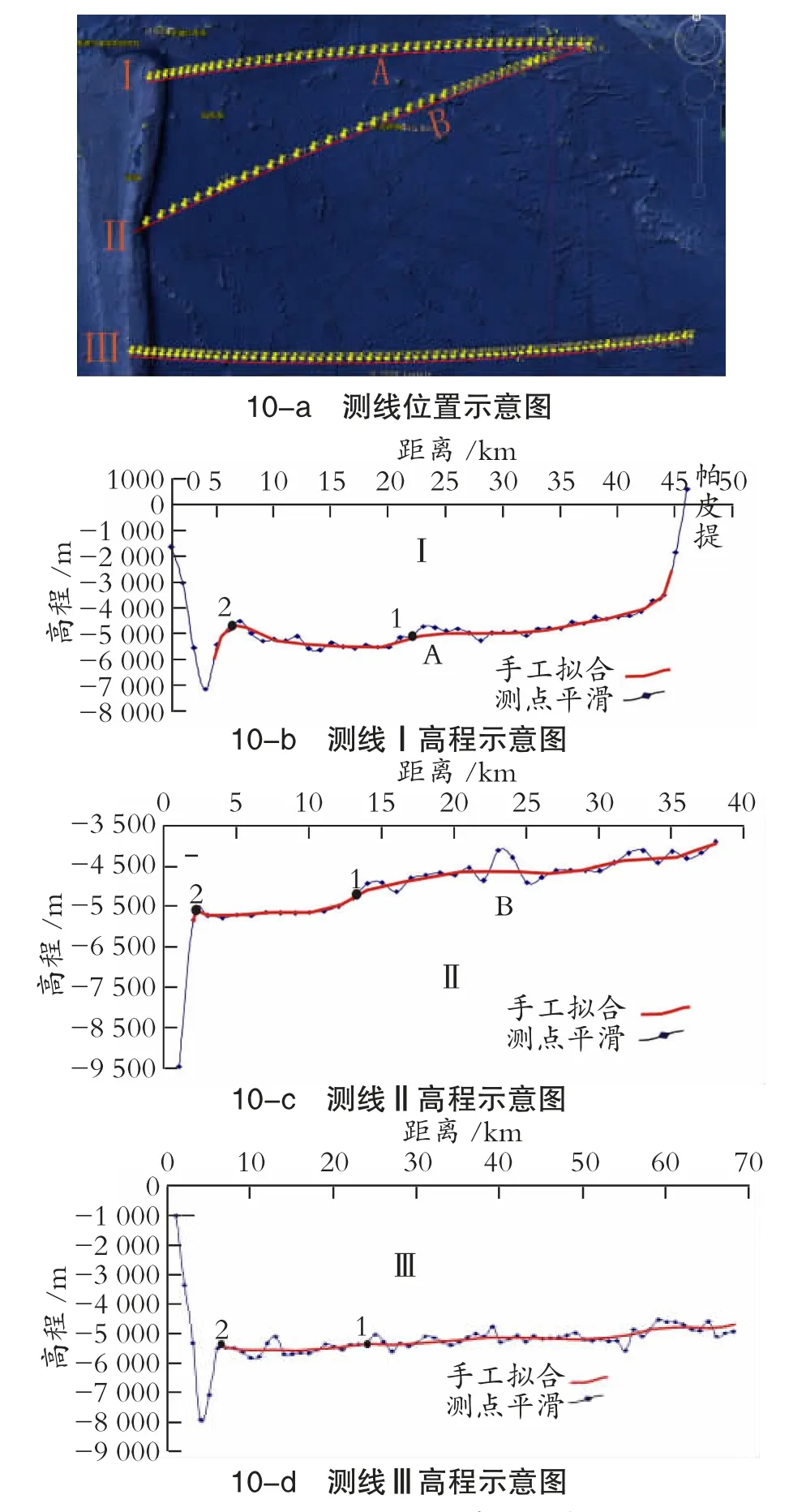
图10 测线位置与测线高程示意图
当然热结构的存在,不止有上面的证据,如海沟吞噬海水[10]太平洋下、大西洋及非洲下存在两个“大型低速切变区”,还可依据图7的重力图的解释等,均可佐证热结构的存在。在文献[8]中还对转换断层,洋脊链,三联点做了理论上的分析,对热结构形成再了解可参考文献[8]。洋底“消失的古陆”的被发现[11],反映了洋低链源热结构的变动与反复,或网源热结构的消失与重建。
6 结束语
通过对地球引力场与自转等的分析,在地球内部建立了由各种力强度的合力强度方程。从合力强度方程看,各家学者在同样的地质体中,提出不同的动力学理论是有道理的,但如何用合力方程解决地质问题,以后还将进一步探讨。然而,随着洋底“消失的古陆”被发现[11];“现今地球上裂谷的伸展并不一样,已经存在的洋中脊分布方向也不统一,为什么会形成这样分布的大洋中脊系统?”等问题提出[12];“板块自驱动模式”[13]等的出现,上述给出的系统性方程也许能解决最后的问题,若这些系统性方程错误可避免重蹈覆辙,若正确或许是一可借鉴的思路,因为本文给出的合力强度适用于地球内部任何一点。

