基于知识空间理论的线性代数的关键学习路径

杨文杰 郑前前

[摘 要] 合理利用线性代数中知识点之间的组织和依赖关系，可以提高学生学习效率及教师的教学质量，然而目前针对线性代数构建知识空间的研究甚少。针对本科生在线性代数学习中的问题，为教育评价提供了一种有效的科学方法，即将知识点与集合论中的元素建立对应关系，基于知识点间的组织和依赖，寻求知识点集合的最小支撑网，利用知识空间理论给出一种线性代数中快速自优化测试过程，使学生能够准确高效地对自己的知识结构、认知缺陷等更细节性内容有一个清晰明确的认识。最终测试结果可以为教师的因材施教提供理论指导，以达到全面了解学生学习状态的目的，同时学生还可以基于已有的测试结果实时掌握个人学习状况，并以此设计符合自己实际情况的学习方案。

[关键词]  知识空间理论;自适应测试;线性代数;矩阵

[基金项目] 2019年度许昌学院教育教学改革研究项目“依赖我校学习通平台的高等数学小班教学研究与实践”（XCU2019-ZZ-022）

[作者简介]  杨文杰（1984—），女，山西大同人，博士，许昌学院数理学院讲师（通信作者），主要人事分支与混沌研究;郑前前

（1988—），男，河南周口人，博士，许昌学院数理学院讲师，主要从事复杂网络动力学研究。

[中图分类号] TP18   [文献标识码] A    [文章编号] 1674-9324（2021）24-0185-04   [收稿日期] 2021-03-06

一、引言

线性代数（Linear Algeria）是数学的一个分支，已成为代数学科的一个重要方向，是高等院校经济类、管理类以及众多理工类专业的重要的基础课之一，它主要包括行列式、矩阵和向量等内容，主要用于解决线性代数关系的问题。为了满足数学的进一步发展，线性代数的应用也在不断地扩大。它不仅是训练学生数学思维方式的重要课程之一，而且是一些专业必修课的必要基础，是为培养适应四个现代化需要的本科层次的多类专业人员而设的一门公共必修课。本课程是学生后续一些专业必修课的基础，对后期的继续学习都具有至关重要的作用。线性代数主要包含行列式、矩阵、线性方程组、向量组，线性空间及线性变换等内容。它的理论内容不仅被用于数学的许多分支，而且在很多领域中都有着广泛的应用。然而一个很现实的问题是，大学新生通常具有中小学课程“填鸭式”教育的惯性思维，又由于大学的课程多而复杂，加之在教学实践过程中学时有限的情况下，学生想要充分理解线性代数中诸如逆序、行列式、矩阵等抽象概念，简直难于上天，并且考虑到学生的个体差异性，该文希望将教育领域中比较流行的知识空间理论应用到线性代数数学。

1983年，美国数学心理学家J.P.Doignon和J.C. Falmagne在知识空间和一类推测系统之间建立了一一对应关系，即将特定领域的知识概念化为一个问题集合。假设一个人在此领域的知识状态是该人所能够解决问题的子集，当所有知识状态的集合对并运算封闭时，称为知识空间。基于此，两位学者给出了一种有效评估知识的数学理论，知识空间理论（Knowledge Space Theory，簡称“KST”）[1]。KST理论为教育过程评价提供了一套合理有效的科学方案，同时也是一种提高学生整体知识掌握水平和搭设学生知识框架的理论。20世纪90年代，Koppen、Doignon开发了一种可通过交互式询问专家来构造知识空间的程序，由此产生的知识空间方法有助于为特定领域构建此类空间[2]。1993年Dowling给出了一种可用于根据专家的判断构建知识空间的基础的方法。以这种方式，可以改进文献[2]中依赖于专家的程序[3]。随后Albert提出了一套由问题系统导向搭设知识理论空间的方法[4，5]。2004年，我国学者傅骞等人利用知识空间扩展理论，从理论上搭建了新型教育资源平台。该平台使教育资源库为教师的教学服务的同时，还可为学生的自我学习、自我评价进行服务[6]。近来，Daniel与Stefano两位学者证明了KST的标准概率模型（例如基本本地独立模型（BLIM）和简单学习模型（SLM））可以表示为MPT模型的特定实例。在这种紧密联系的情况下，MPT方法可用于解决KST中的理论和实践问题[7]。然而学者们多是利用知识空间理论针对中小学生进行能力提升的研究[8]，或是基于知识空间理论进行图书馆阅读推广平台的建设[9]等，而针对本科生的学习效率或能力提升的研究还不多见，故本文将知识空间理论应用于本科线性代数的矩阵这一内容的学习中，以期能够对学生的矩阵这一部分内容的学习有所助益。

二、线性代数中的知识空间

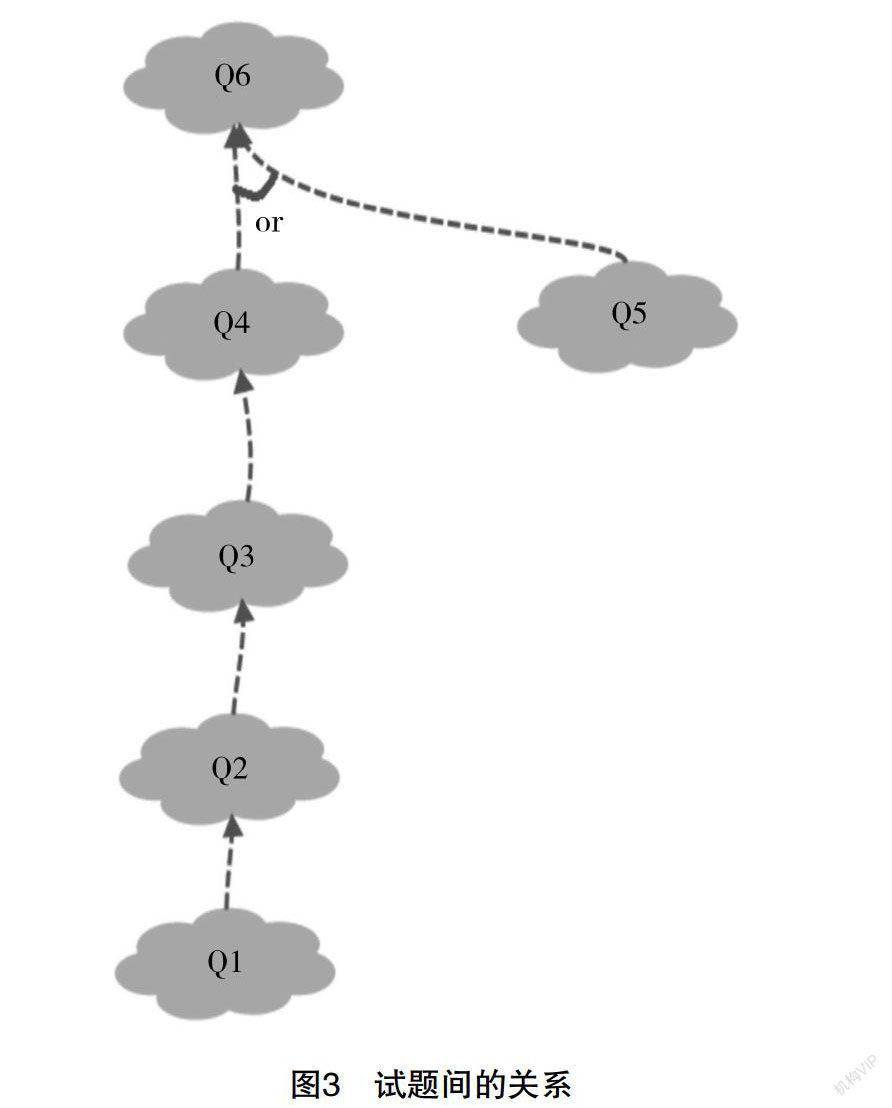
针对线性代数的知识空间问题，本文根据KST理论，给出了一种线性代数中快速自优化测试过程。自优化过程需要基于学生的理论知识掌握程度自优化的选择下一步测试题目的难易程度，故学生的知识网络结构不仅可以由其最后的知识状态确定，而且学生的知识水平以及学生的认知能力缺陷还可以通过计算学生最后知识水平与知识空间之间的集合对称差进行确定。最终测试结果可以为教师的因材施教提供理论指导，以达到全面了解学习状态的目的，同时学生还可以基于已有的测试结果实时掌握个人学习状况，并以此设计符合自己实际情况的学习方案。

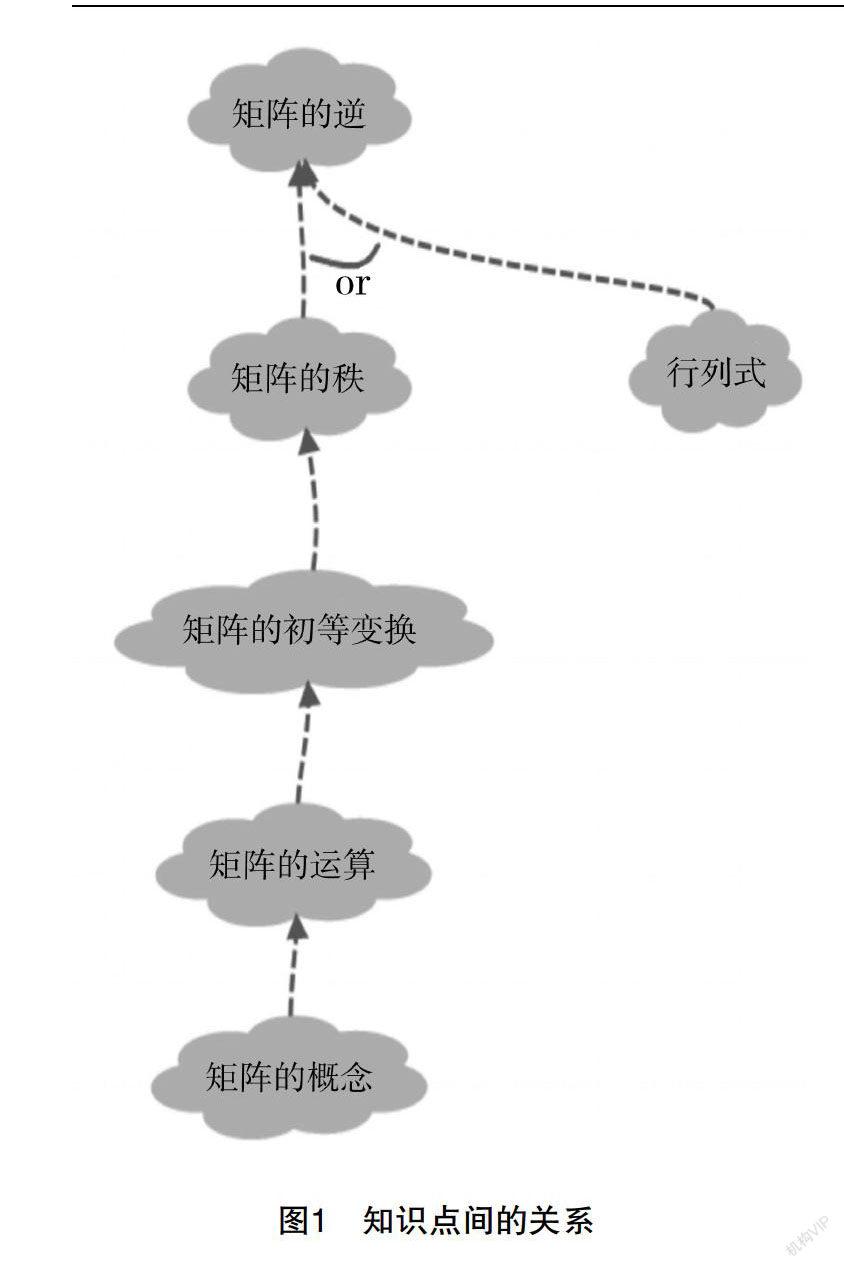
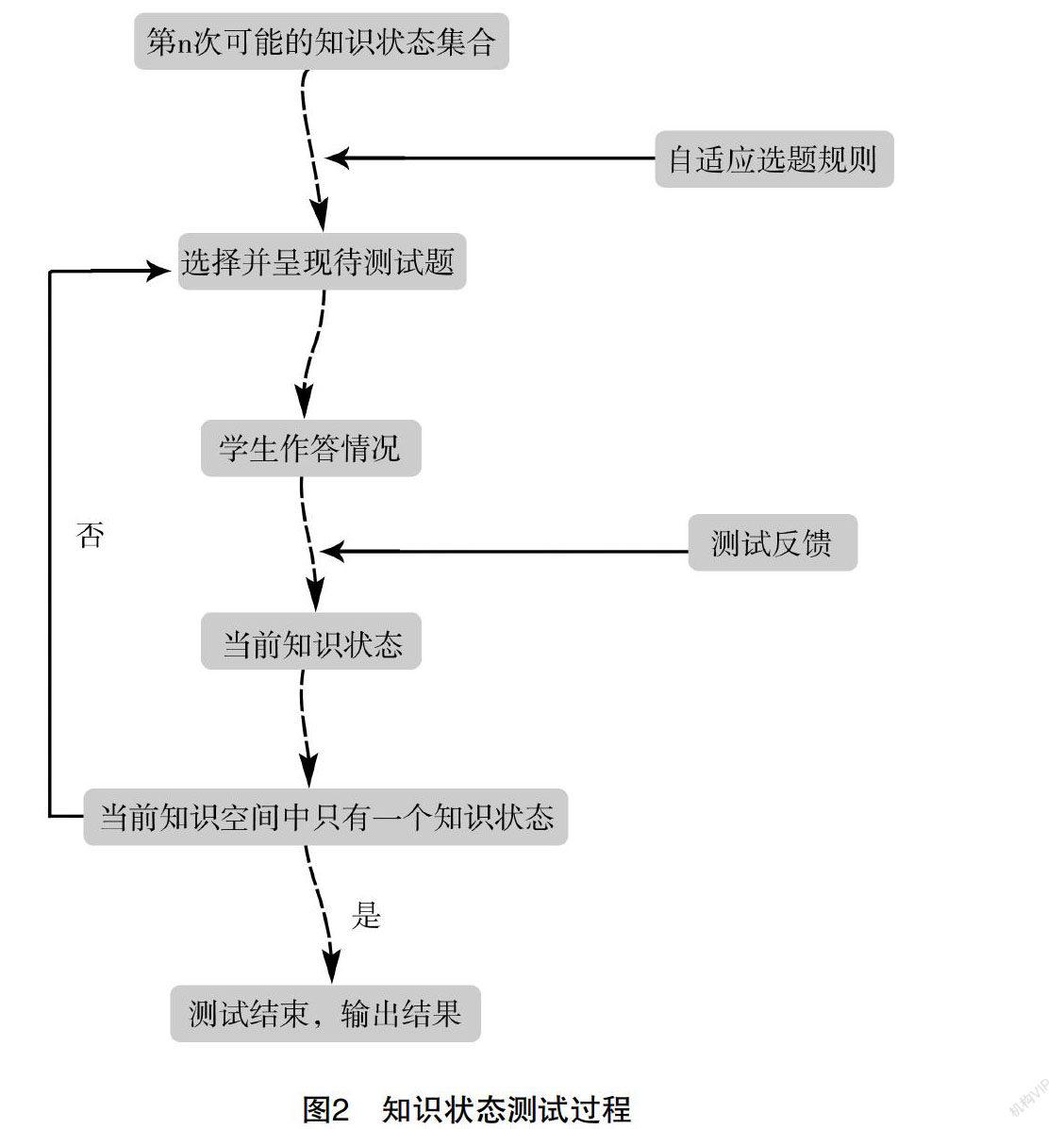
本文将对线性代数中矩阵这部分学习内容进行合理规划，以单个知识点的形式独立列出并进行现有课程掌握水平的测试。从独立知识点的方面研究KST理论，（Q，K）结构中Q为线性代数领域相关知识点组成的集合，K代表现有知识储备情况组成的集合，k■为具体知识点;假设Q为一个有限集合，则称K是其相应的知识空间。根据研究发现[ 10 ]，知识点元素之间的关系主要包括：框架组织、从属依赖;知识框架组织关系以目前使用书本的组织结构框架为准，而元素间的从属依赖关系内含有明显的知识学习先后关系，即某一个知识点是学习另外一个关于知识点的先决条件，故在知识点处理方面，本文主要使用从属依赖这一关系。