基于半导体激光器的Tornambe控制算法研究

郝晓剑，张罗新

(中北大学 仪器科学与动态测试教育部重点实验室，太原 030051)

引 言

在当前的温度测量中，热电偶由于结构简单、性能稳定、测量范围广等优点，成为温度测量领域的重要工具。随着大量快速响应的新型热电偶的开发，如何准确获取热电偶的性能指标成为当前科研工作的一大难题。除此之外，瞬态温度的测量也越来越成为行业热门话题。因此，对热电偶的性能指标就提出了更高的要求[1]。时间常数可以在很大程度上表征热电偶的动态性能，它不仅是保证精准动态测温的基础，同时也能够在很大程度上影响热电偶的非静态测温误差。如何在热电偶的测温端形成一个定量的温度阶跃是当前热电偶时间常数测试的重点。激光具有极高的能量，它可在很短的时间内在热电偶测温端形成高温，可以作为热电偶时间常数测量的理想加热源[2-10]。

在本系统中，主要是以半导体激光器作为热电偶的加热装置，采用PDI-4型光电探测器实时在线监测热电偶测温端的温度变化，然后反馈给控制模块来控制激光器的功率，保证在很短的时间内产生所要求的温度阶跃，进而完成热电偶时间常数的测试。在反馈控制模块的选取上，选择当前应用比较广泛的是比例-积分-微分(proportion-integration-differentiation，PID)模块，它的原理简单、使用范围广、易被人们理解和掌握，但是PID控制器在面对外界扰动时的抗干扰能力较差，因此需要更好的控制算法来完成实验[11-18]。

1 热电偶时间常数测试系统和测试原理

本文中所采用的测试系统主要是由主控制器、大功率半导体激光器、光学整形模块、椭球面反射镜、热电偶、红外辐射测温模块、信号调理电路、数据采集模块、模/数转换器(analog-to-digital converter，ADC)和反馈控制模块等组成。系统框图如图1所示。

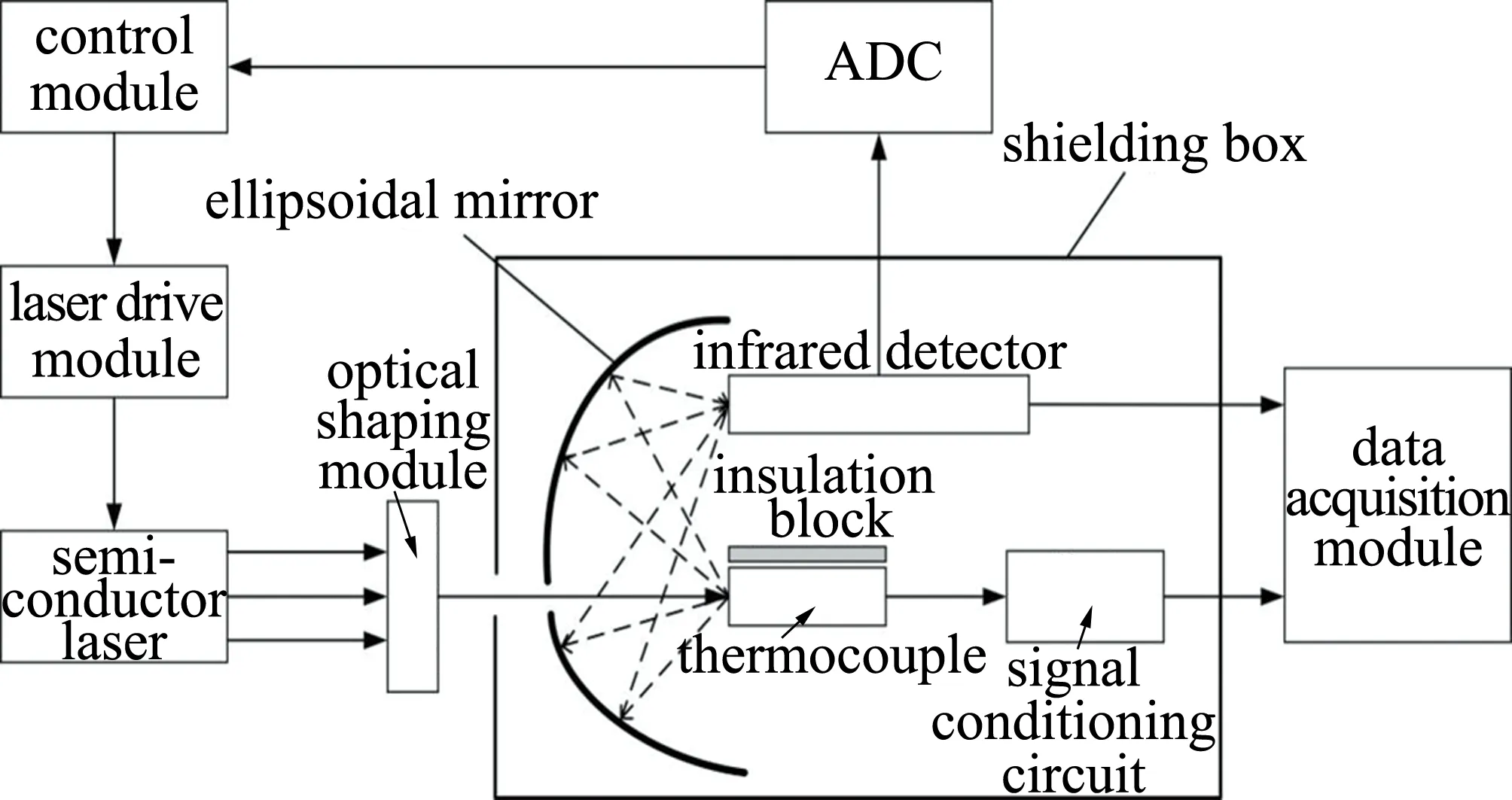
Fig.1 General structure diagram of thermocouple time constant test

在此实验系统中，半导体激光器作为被测热电偶的阶跃激励源，其内部的激光二极管可以被高频电流所调制，改变输出功率，在很短的时间内实现热电偶测温端的温度阶跃。所使用的半导体激光器的工作模式有固定功率输出和变功率输出两种模式，在实验中采用变功率输出模式。被测热电偶与红外探测模块分别置于椭球面反射镜的两个共轭焦点处，在热电偶受到激光激励后，椭球面反射镜可以将其所产生的红外辐射汇聚到红外探测模块，由于红外辐射探测器的优点在于其反应速度远远快于热电偶，因此可以将其作为热电偶表面温度的真值，通过ADC输入到控制模块，然后控制模块通过PID控制器或者Tornambe控制器反馈控制激光器的输出功率，以此在热电偶表面达到期望温度。最后信号调理电路和数据采集模块采集热电偶在工作中的时间-电压响应曲线，通过分析热电偶的时间-电压响应曲线，得到热电偶在不同控制器下的时间常数。

热电偶一般被作为1阶系统，在时间常数的测试实验中，不考虑热电偶传热能量和辐射能量的散失，可得如下公式：

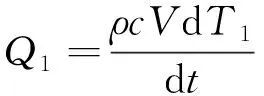
(1)

Q2=hS(T2-T1)

(2)

式中，Q1为热电偶测量端储热量，Q2为热电偶对流传热量，ρ为热电偶测量端密度，c为热电偶测量端比热容，V为热电偶测量端体积，T1为热电偶测量端温度，T2为介质温度，h为对流换热系数，S为测量端换热面积。

设τ=ρcV/(hS)，根据(1)式、(2)式整理可得1阶微分方程：

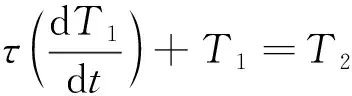
(3)

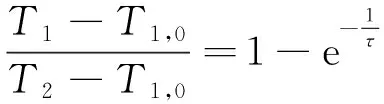
(4)

根据(4)式可以得到，当t=τ时，热电偶表面温度达到阶跃温度的63.2%，τ即为热电偶的时间常数。

热电偶时间常数测试的理想输出曲线如图2所示。横坐标为时间t，纵坐标为温度T，T0为热电偶起始时刻的温度，T3为稳定温度，t1为起始时刻，t2为热电偶表面温度达到阶跃温度的63.2%的时刻。

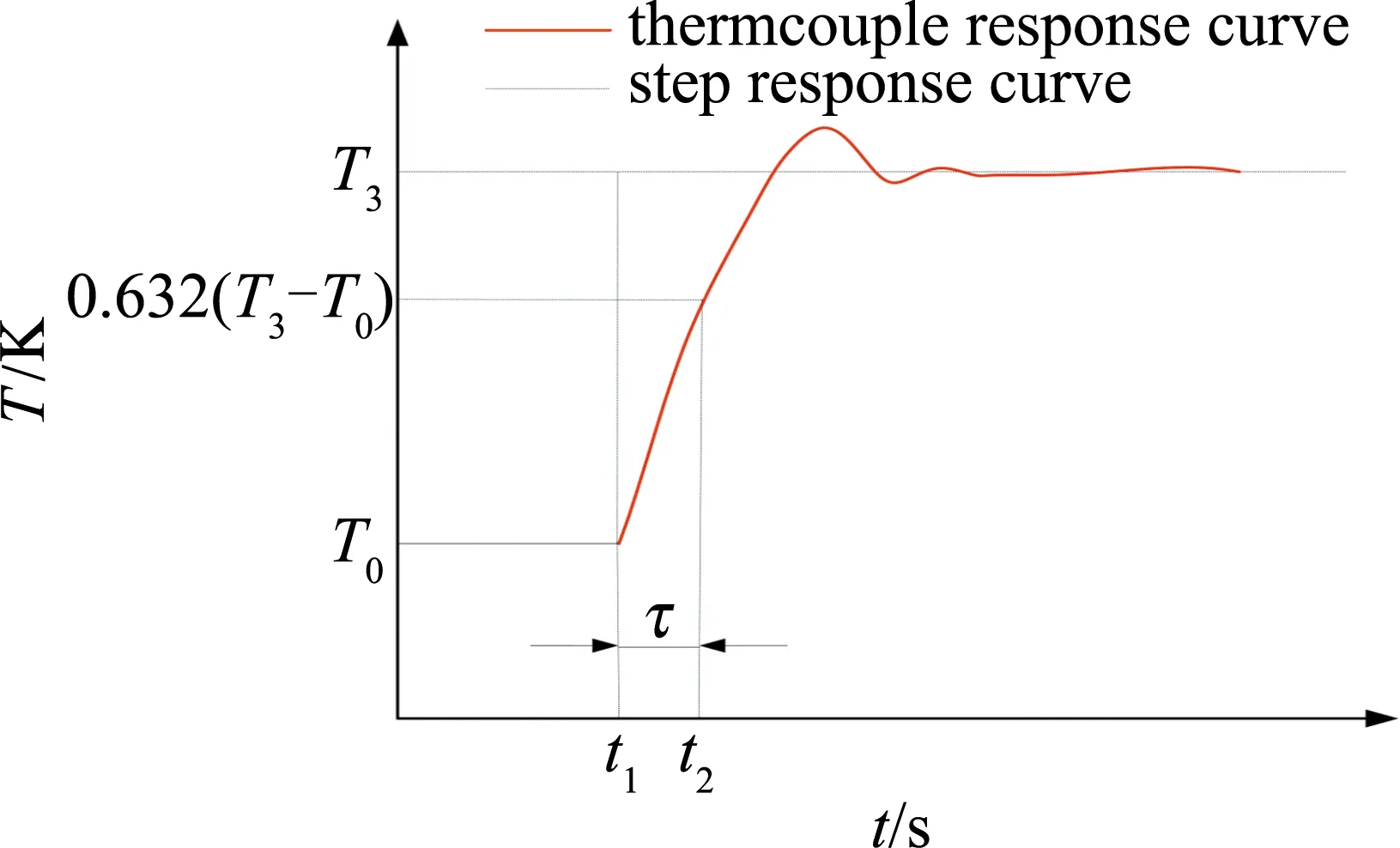
Fig.2 Thermocouple response curve

2 Tornambe控制器的设计

Tornambe控制算法是一种基于主动补偿的控制方法，其基本原理是利用扩张状态观测器，实现对非线性系统各种不确定性的主动估计和动态补偿，进而实现对系统的有效控制。它与其它控制算法的最大区别是不依赖于精确的系统数学模型，核心在于构造观测器来对扰动进行估计和补偿，最终实现对动态系统的反馈控制，因此，对这一控制算法的研究一直受到人们的广泛关注[19-21]。

单变量非线性数学模型表示如下：

(5)

式中，R是实数集，x表示系统状态，f(x)和g(x)为系统已知的有界非线性函数，u为系统的控制输入，h(x)为系统输出。对于(5)式所示系统，假设相对阶r已知且输出y及y(i)(1≤i≤(r-1))可测，则有微分变换:

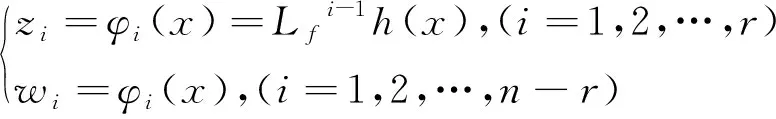
(6)

式中，φi(x)为中间函数，Lf为所代表的非线性系统，f为光滑函数,则可以得到下式：

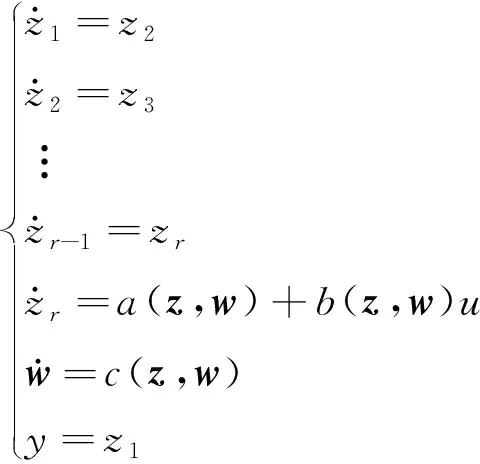
(7)

式中，z=(z1,z2,…,zr)T；w=(w1,w2,…,wn-r)T；a(z,w)，b(z,w)和c(z,w)可由f(x)，g(x)，h(x)和微分变换函数得到。

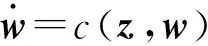
y(r)+hr-1y(r-1)+…+h1y(1)+h0y=r

(8)

式中，h0，h1，…，hr-1为系统的动力学参量，在保证系统稳定性的前提要求下，hi(i=0,1,2,…,r-1)的选取必须保证系统的闭环极点位于s的开左半平面，即特征方程sr+hr-1sr-1+…+h2s2+h1s+h0=0的根位于s的开左半平面。

在满足上述条件下，将扩张状态定义为：

d(z,w,u)=a(z,w)+[b(z,w)-1]u

(9)

u=-h0z1-h1z2-…-hr-1zr-d(z,w,u)

(10)

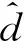
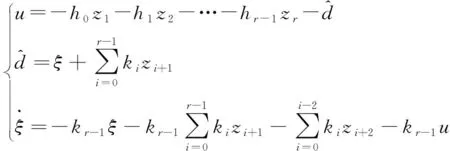
(11)

式中，k0,k1,…,kr-2为任意常数，kr-1=sgn(b(z,w))μ，μ为一正值常数，μ的选取决定了系统的稳定性；ki(i=0,1,…,r-2)为任意常数，主要影响系统的控制性能。如果存在常数μ*>0，当μ>μ*时，方程组(5)式和(11)式所示闭环系统是渐进稳定的。

取r=2，得到2阶Tornambe控制器的控制方程为：

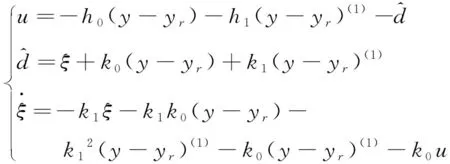
(12)

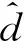
3 Tornambe控制仿真

2阶Tornambe控制器的Simulink结构图如图3所示。

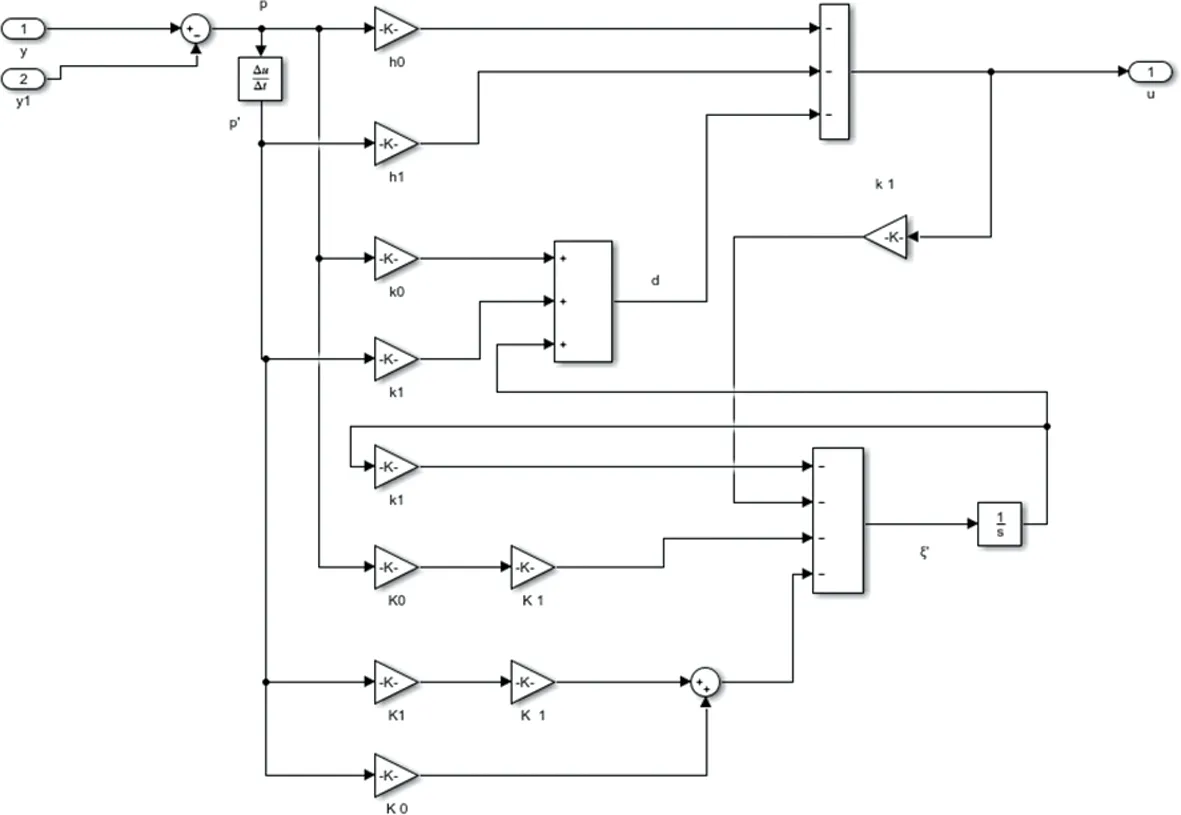
Fig.3 Second order Tornambe controller

针对2阶单变量非线性Tornambe控制器，有4个参量需要进行整定，分别是h0,h1,k0和k1，它们都是系统的可调参量。在ki不变的情况下，hi增大，系统能更快趋于稳定，达到输入幅值；在hi不变的情况下，ki增大，系统的抗干扰能力变差。在MATLAB下的Simulink模块中分别采用Tornambe控制算法和PID控制算法进行系统仿真，得到仿真结果如图4所示。

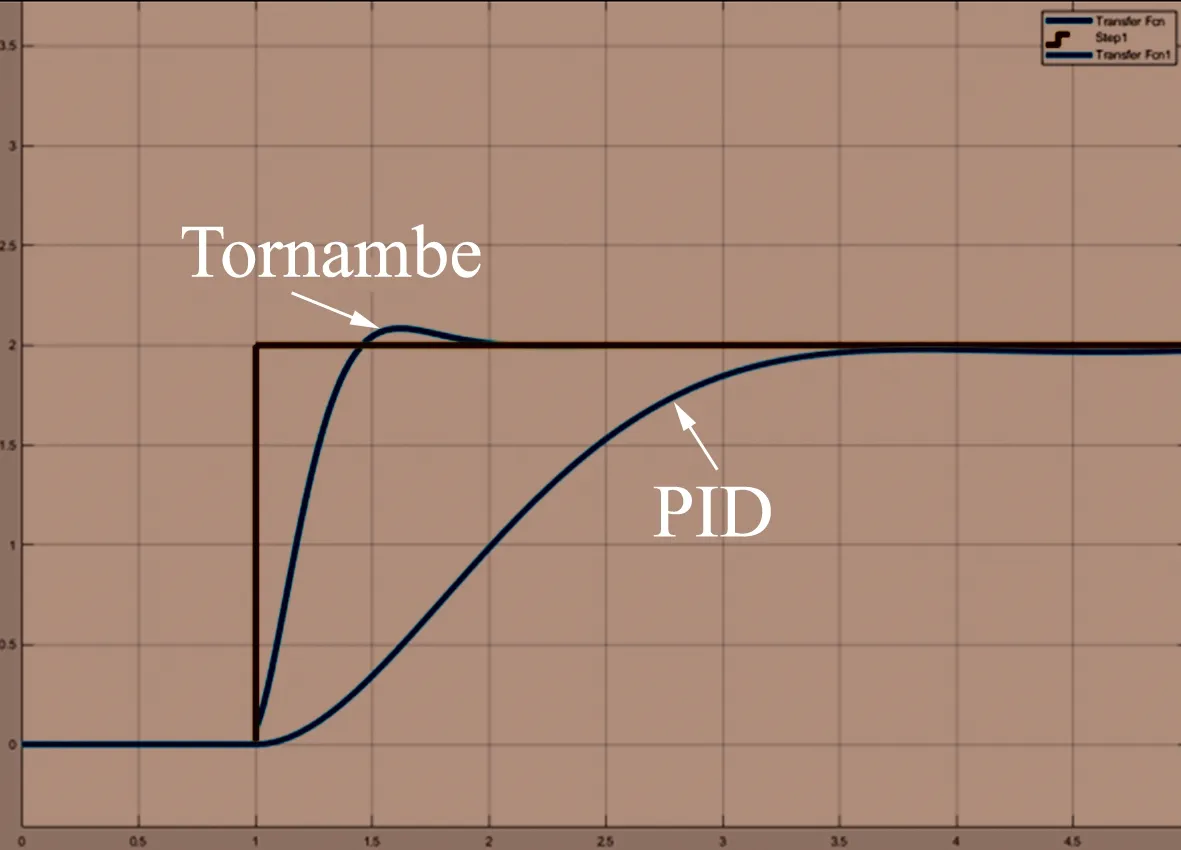
Fig.4 Tornambe control and PID control algorithm simulation

从图4中可以看出，在同样的系统条件下，Tor-nambe控制算法下，阶跃信号的上升时间为0.7s，达到稳定期望信号所用的时间为1s，超调量为4.75%，而在PID控制算法下，阶跃信号的上升时间为2.5s，达到稳定期望信号所用时间为2.5s，超调量为0。仿真结果表明，Tornambe控制算法下的阶跃信号上升沿更快，达到稳定期望信号所用的时间更短，而由于PID算法的参量设置更加合理，因此超调量要小于Tornambe算法。

4 实验验证

在温度25℃、湿度55%、标准大气压环境下，以上面所提到的时间常数测试系统为实验基础，所采用的半导体激光器的光谱曲线图如图5所示，工作参量如表1所示。分别采用Tornambe控制器和PID控制器对CO1-K型热电偶进行测试，数据采集卡采集得到热电偶的时间-电压输出电压响应曲线如图6所示。

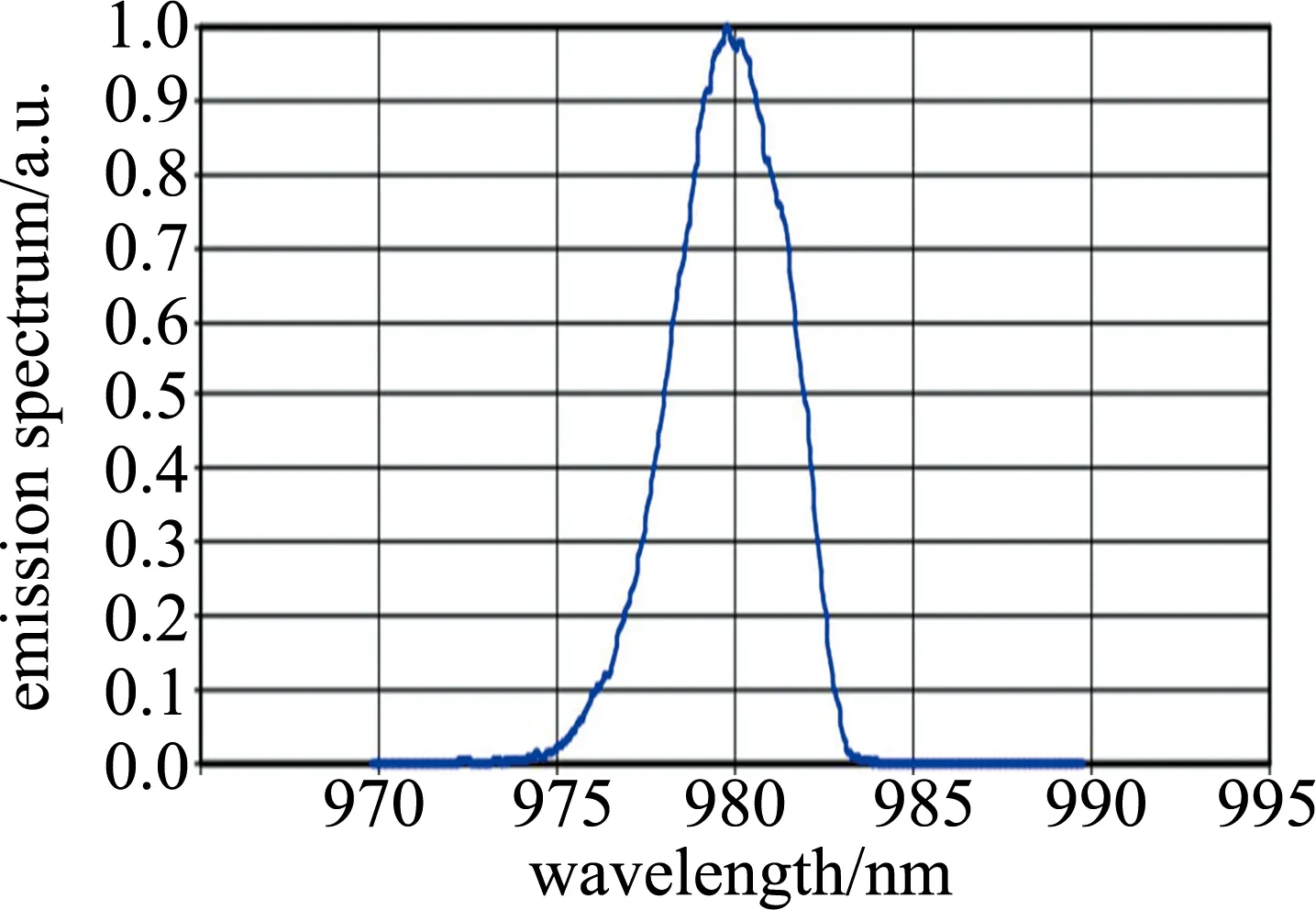
Fig.5 Spectral curves of semiconductor lasers

Table 1 Operating parameters of semiconductor laser

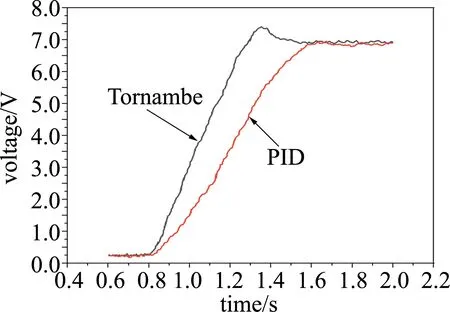
Fig.6 Tornambe and PID control effect comparison experiment

在LabVIEW中可以很直观地得到在这两种不同的控制方法下，热电偶的电压信号上升时间、超调量和时间常数，分析结果如表2所示。

通过上述实验数据对比可以发现：在同一硬件系统下，CO1-K型热电偶在传统PID控制下所测得的时间常数为456.2ms，在Tornambe控制下的时间常数测试结果为284.6ms;从实验结果中可以发现，相较于传统的PID控制算法，Tornambe控制下的系统达到稳态所需要的时间更短，阶跃温升源的上升时间更短，因此在实验中，热电偶受到激励后的响应时间更短，速度更快。在控制器的参量设置上，PID控制器中参量设置合理，所以超调量为0，Tornambe控制器中h参量设置较大，使得系统可以更快达到预期设定目标。虽然在Tornambe控制下出现了6.47%的超调量，但是在允许范围内，对实验结果没有太大影响。

Table 2 CO1-K thermocouple measurement results

5 结 论

本文中设计了一种热电偶时间常数测试系统，利用大功率半导体激光器来作为被测热电偶的阶跃激励源，分别采用新型Tornambe控制算法和传统PID控制算法来实现半导体激光器功率的反馈控制，结果表明，在670℃的期望阶跃温度下，Tornambe控制器可以更好地实现热电偶的阶跃温升，相比传统PID控制算法下所测得的热电偶时间常数更小，大大降低了热电偶时间常数测试中的误差，提高了实验测试的准确性，具有较强的现实意义。