基于非参数估计的风电场储能容量优化研究
王超平,刘海英,贝前程,裴云成
齐鲁工业大学(山东省科学院) 电气工程与自动化学院,济南 250353
风电能源具有绿色环保、可再生的特点,大规模风电场并入电力系统后,其风能的不确定性和不稳定性对电力系统稳定性及电能品质产生较大影响,从而危害电网正常运行[1]。因此,在制定发电和调度方案时,应先运用风电预测来解决风力发电的不定性和不稳定性产生的问题,然后利用储能的动态输入和释放来弥补风电的不足,使风电输出可控。
文献[2]指出风电预测存在较大误差,影响系统的备用容量和功率平衡。文献[3]指出国内外存在解决风电接入、电网调度困难等问题,缺少较为准确的风电功率预测技术手段。
风电功率预测后,利用储能系统可降低风能波动性的影响、使风电功率更加稳定[4]。文献[5]提供了经济效益最大化的储能系统容量配置的方法。文献[6]提供了运用储能系统来降低风电调度风险的方法,但以上方法受恶劣天气等外部干扰。
采用非参数估计的储能容量配置方法可忽略外部干扰,在给定条件下进行统计分析,可获得较为理想的效果。作为非参数估计的一种,核密度估计可更好地描述连续的密度函数[7]。该方法对数据分布不附加任何假定,只从数据本身特征出发研究其分布特性[8]。本文通过运用非参数核密度估计的方法,计算置信区间和储能系统的额定容量,配置合适容量的储能设备,使风电场输出功率平滑输出,解决了由于风能不确定性和不稳定性造成的风电预测误差较大的缺陷。
1 风电功率预测误差与置信区间
风能的不确定性和不稳定性会影响预测的准确度,从而带来调度压力,如何使风电功率预测更精确已成为研究热点。
1.1 风电功率预测误差概率分布
目前,风电功率预测主要有基于风电功率历史数据和基于数值天气预报两种预测误差估计模型,为提高预测的精准度,两种方法均须进行大量数据分析,耗时较长[9]。
但实际上,风电机组输出功率受风电功率预测算法、模型精确性和气候环境等因素影响,其实际值与预测值大多是存在差异的,故两种方法选择差别不大。图1对美国俄州某风电场公布的2014年数据选择其中5 d的风电功率实测值和预测值进行比较,其采样点间隔为10 min。
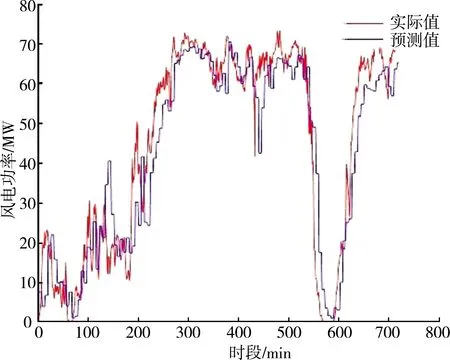
图1 风电场实测功率与预测功率对比
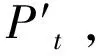
上述风电场风电预测误差如图2所示。
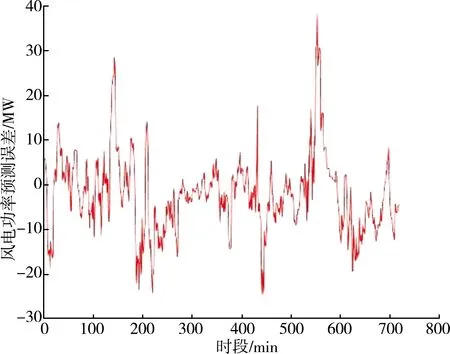
图2 风电场风电预测误差时刻图
1.1.1 非参数核密度估计理论
常用的非参数密度估计法有图密度和核密度两种估计法。图密度法简单易用,但结果是间歇性的[10]。由于核密度估计法能够对样本数据进行最大程度得近似,效率损失较小,因此本文选用核密度估计法,其通用表达式为
(1)
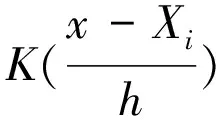
1.1.2 风电功率预测误差概率分布
在风电功率预测误差拟合中,利用美国俄州某风电场数据,使用标准的高斯核函数
(2)
作为核函数来进行非参数核密度估计[12]。
对风电功率预测误差的概率密度分布拟合,并将非参数核密度估计与正态分布及频率分布直方图进行直观对比如图3所示。
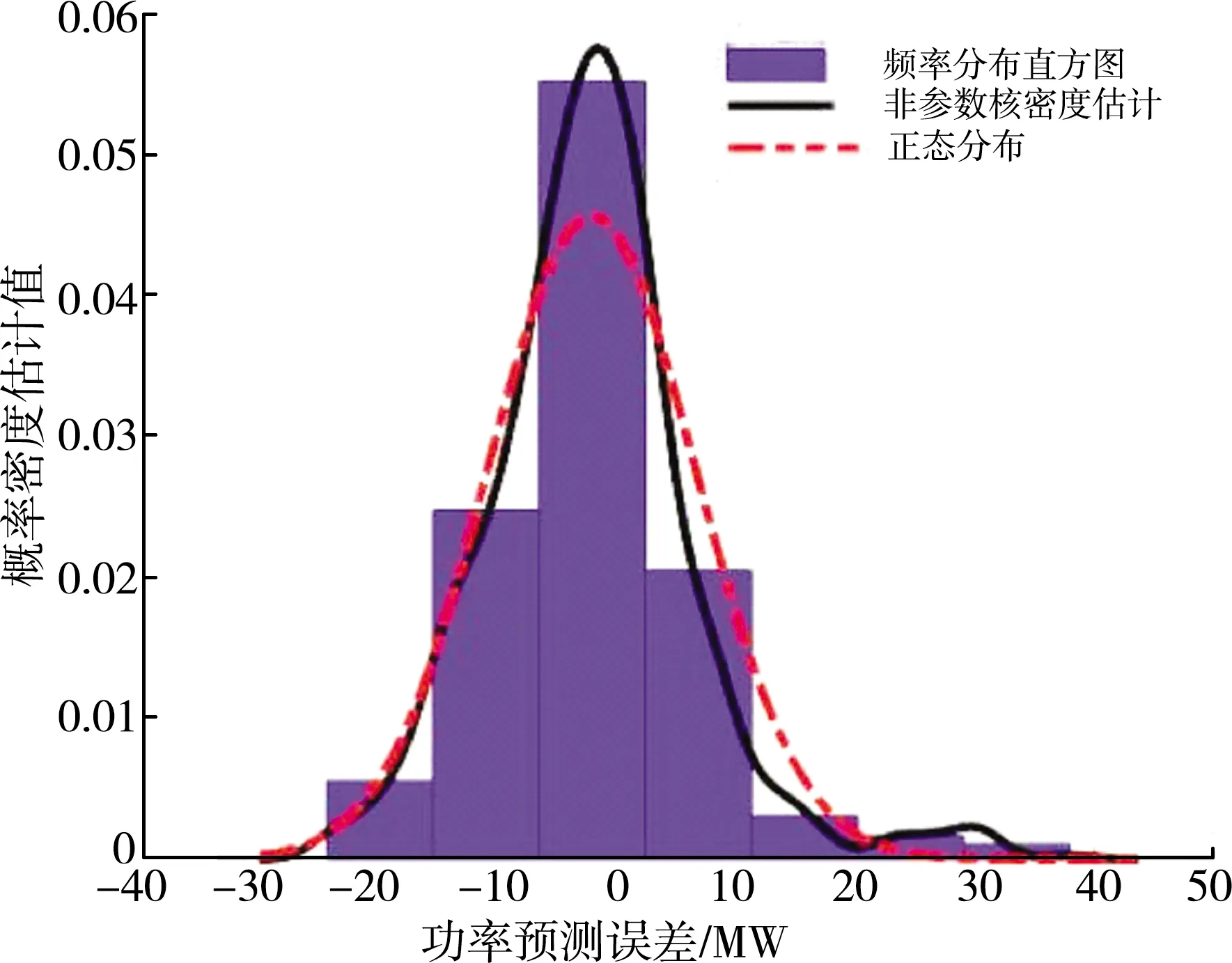
图3 风电功率预测误差概率密度
从图3可以发现,非参数核密度估计方法对比于频率分布直方图和正态分布,求得的概率密度估计函数对于风功率预测误差以及累计风电功率误差的拟合效果都不错,由MATLAB计算其最佳带宽为1.912 5 dB[13]。
1.2 风电功率预测误差置信区间估计
1.2.1 置信区间估计方法
置信区间估计是描述预测值对比实际值的随机性惯用方式,可以量化随机性产生的风电功率预测结果变动,为风电场运行管理者传递更丰富的信息[14]。本文中风电功率预测误差的置信区间采用该方法来估算。
假定预测误差的随机变量是预测误差的累计概率分布函数,满足置信概率为1-α的风电功率实际值的置信区间为[Xα1,Xα2]。其中:Xα1为累计概率分布函数为α/2的x的值;Xα2为累计概率分布函数为1-α/2的x的值。
1.2.2 求置信区间
采用对称法求置信区间,用MATLAB软件来编写程序,利用核密度概率分布函数计算区间的上下分位点,具体步骤如下。
先读取5 d风电厂功率预测误差数据,再做出核函数概率密度曲线图4所示。
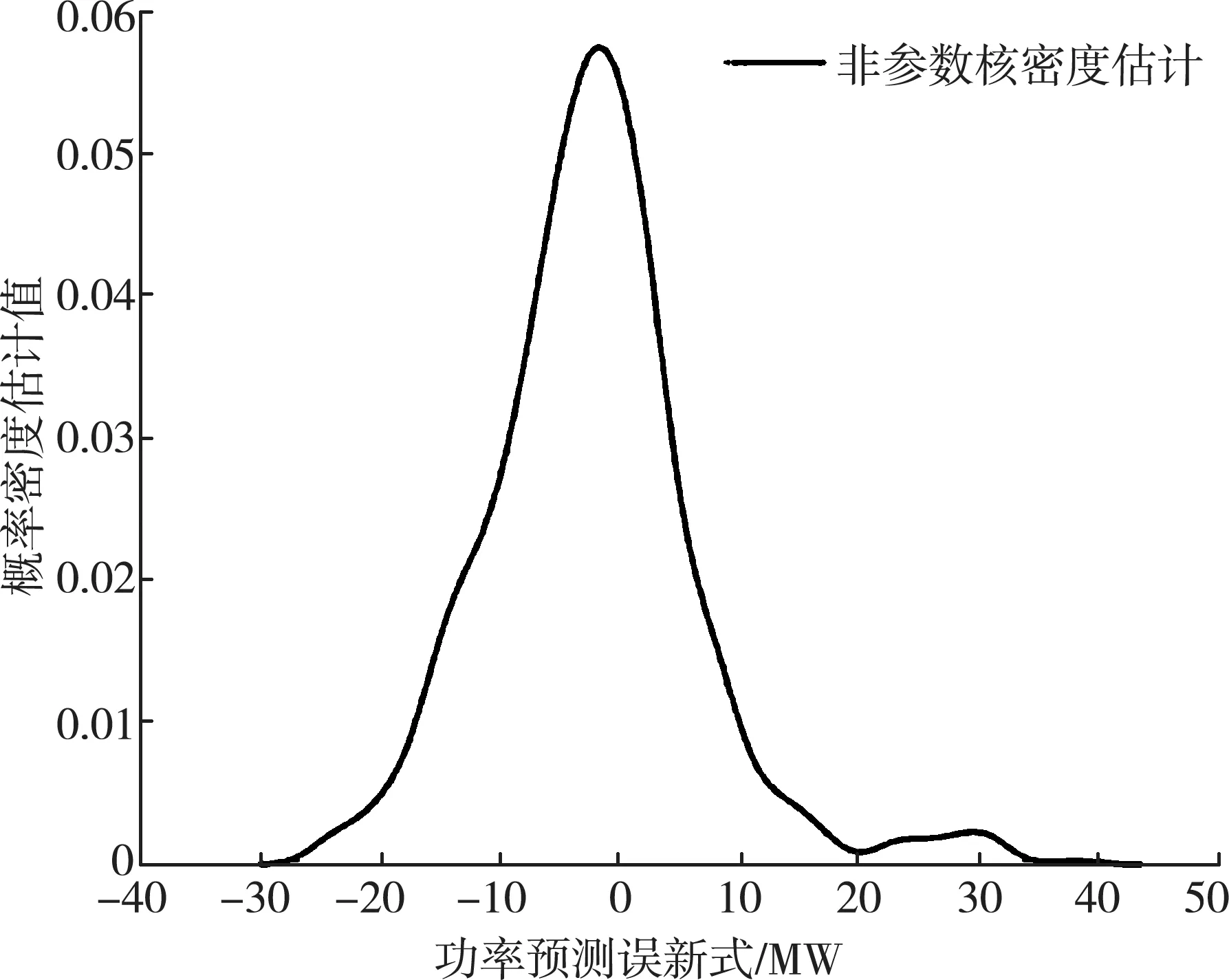
图4 非参数核密度估计
采用超短期预测[15],取其中部分风电功率预测误差数据如表1所示。
最后编写程序,计算90%、85%、80%置信度下的置信区间上下分位点,做出相对应的非参数核函数概率密度分布如图5所示。
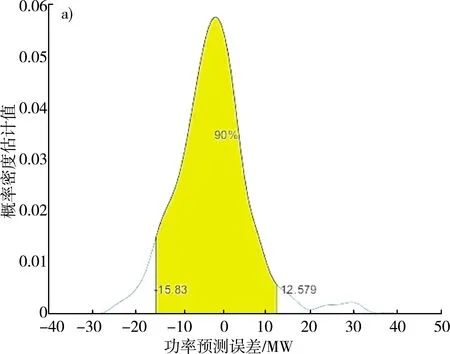
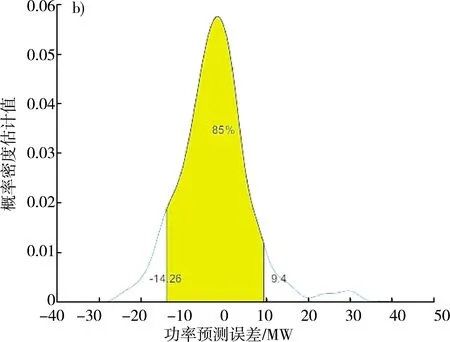
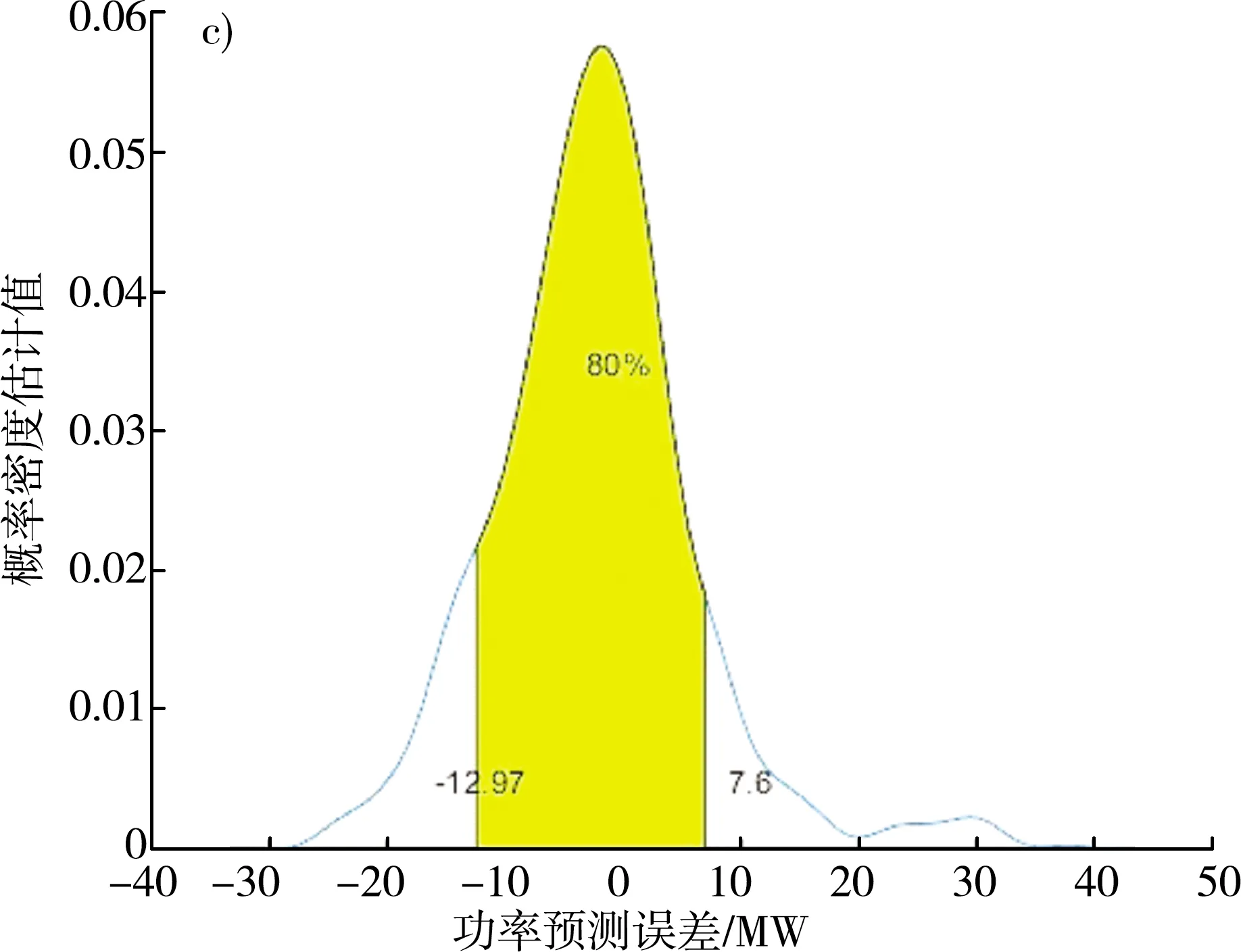
注:a)置信度为90%;b)置信度为85%;c)置信度为80%。
由此可见,置信度越高,置信区间长度越长,阴影覆盖面积增大,而相应的置信区间的估计误差会减少。
置信区间的长度等于上下分位点之间的距离,通过计算置信水平90%、85%、80%下的区间长度分别为28.409、23.660、20.583。
通过比较28.409>23.66>20.583可知,置信度为80%时置信区间长度最短。表2为不同置信度下的置信区间。
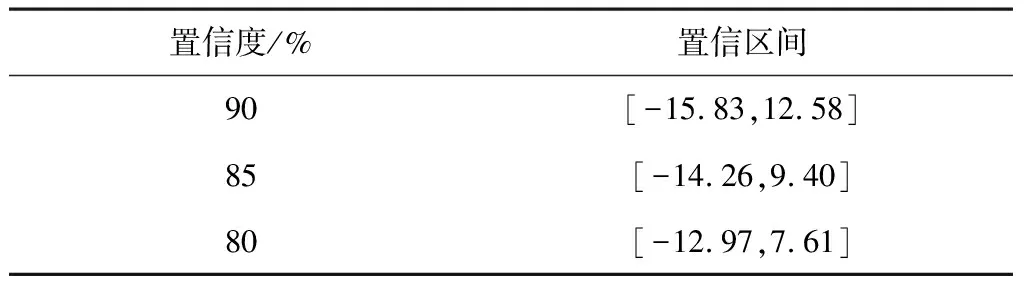
表2 不同置信度下的置信区间
2 储能容量的配置
储能系统(Energy Storage System,ESS)的充放电特性可解决风电功率输出不稳定的问题,是提高风电系统暂态稳定特性的关键。
2.1 ESS功率的确定
2.1.1 功率的算法
合理的配置要求ESS能够具有足够的充放电功率,最大充放电功率可以利用风电输出功率预测的大数据计算得到。
本文中风电场输出功率的预测值直接采用美国风电场数据中B列风电预测功率P0,所需要的ESS输出功率为E列风电预测功率误差Pb0,也就是P0与C列风电实际功率的差值Pg。
Pb0[n]=P0[n]-Pg[n]。
(3)
式中:n为采样次数;Pb0[n]为第n次采样E列风电预测功率误差,其数值正负代表ESS的放电和充电状态;P0[n]、Pg[n]分别为第n次采样的风电预测功率和风电实际功率的差值;NEs为ESS总体效率。依照需要的ESS出力功率,探求ESS总体效率,能够找到适当的ESS充放电功率的实际值,用Pb0[n]来表示:
(4)
式中:NEs.d为ESS的放电效率;NEs.c为ESS的充电效率,若假设充放电效率相同,则ESS充放电效率为1时,ESS工作过程中满足的理想条件应是净充(放)电电量为零,即
(5)
式中:TS为采样的时间跨度,s;Ns为总采样次数。由于,ESS的充放电过程中存在能量损耗,其实际效率NEs低于100%,即ΔE>0。为保证ESS系统的实际输出功率满足式(6)约束条件,可把P0整个向下移动,ΔP是储能系统计划输出功率的平移量,其通过迭代法求得。平移之后系统功率目标输出用Pa[n]表示,则
Pa[n]=P0[n]-ΔP。
(6)
减去平移量之后的系统目标功率输出Pa,所需ESS的功率输出为
Pb0[n]=Pa[n]-Pg[n]。
(7)
通过式(2)至式(5)可获得ESS实际充放电功率值。再利用式(2)至式(6),便可得到ESS实际充放电功率的最大值,即额定功率。
Peso=max(|Pb[n]|)。
(8)
2.1.2 计算额定功率
利用美国某风电场5 d的功率数据,计算额定功率得平移量ΔP为0.385 8 MW,ESS额定功率为42.539 8 MW。ESS系统的功率输出曲线如图6所示,输出功率为负值,表示ESS为充电状态。
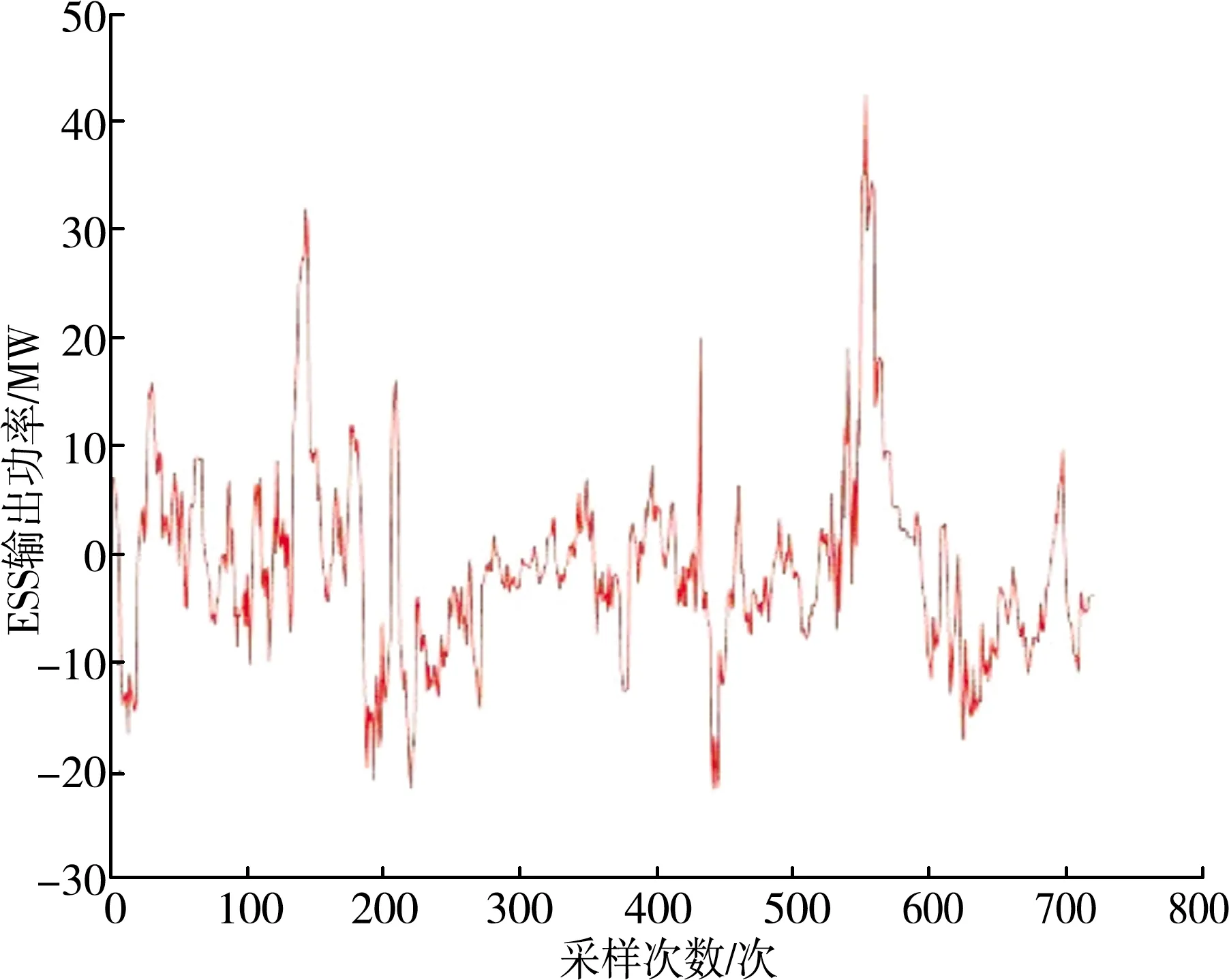
图6 平移后ESS功率输出图
2.1.3 利用核密度估计求置信区间优化ESS输出功率
利用核密度估计法将ESS输出功率数据进一步优化,这里采用90%置信度,以便对ESS额定容量的最优化求解,缩小风能波动性造成的误差。
优化后的ESS输出功率最大值为14.38 MW,最小值为-13.956 MW。优化后得到ESS系统输出功率时刻图,如图7。
科尔沁沙地(41°41′41″~45°12′15″N, 116°25′33″~123°42′52″E)位于松嫩草原向内蒙古高原的过渡地带,总面积57451 km2[32],海拔 87~2014 m,属于大陆性季风气候,是我国距离海洋最近的沙地[33, 34]。科尔沁沙地的年均温度、年均降水及海拔分布详见图1。
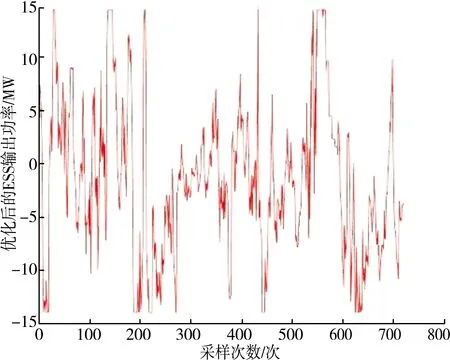
图7 优化后的ESS系统输出功率时刻图
2.2 ESS容量的确定
为达到平滑可再生能源功率输出波动的要求[9],可使用仿真法得出ESS所需要的最大容量,其运算方法如下:
1)以确定的ESS实际输出功率数据为基础,记录各取样点处的ESS充放电电量,得到各取样时刻ESS相比于起始状态的能量波动,即
m=0,1,...,NS。
(9)
式中:NS为样本总量;Eb,acu[m]为前m个采样周期内ESS累计充放电能量总数,单位为MWh。
2)在整个样本数据周期内,由于ESS存在能量波动,计算ESS最大、最小能量之差,考虑SOC限制,获取ESS容量的额定值:
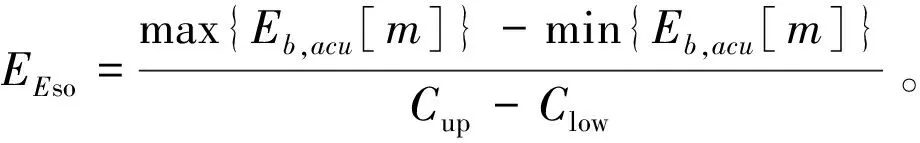
(10)
式中:Cup和Clow分别指ESS运行SOC上、下限约束;max{Eb,acu[m]}、min{Eb,acu[m]}分别指ESS相比于起始状态最小、最大能量。
利用式(10)和式(11)和之前得到ESS输出功率的数据计算出整个样本数据周期内的最大和最小能量值,以及估算出该风电场适合用于平滑风电出力的ESS额定容量,这里我们设0.9和0.1分别指ESS运行SOC的上下限约束。
ESS补偿风电预测误差最理想的状态是全补偿,即不考虑充放电转换效率和能量损耗。本文采用美国某风电场第一天的数据计算额定容量并作出当天的ESS的能量波动图。
由此可知,该美国某风电场第1天的ESS系统的额定功率为31.559 MW,额定容量为73.865 MWh,图8为第一天ESS系统出力的能量波动图。

图8 第一天全补偿的ESS系统出力的能量波动图
2.2.2 90%置信度下的额定容量
考虑到ESS的实际效率和能量损耗,选择90%置信度。本文依旧采用美国风电场第一天的数据利用之前的公式计算ESS的额定容量。已知90%置信区间为[-13.96,14.38],减去平移量后过滤掉超出90%置信区间的ESS输出功率。求得系统的额定功率为14.38 MW,额定容量为53.42 MWh,图9为90%置信度下ESS系统出力的能量波动图。
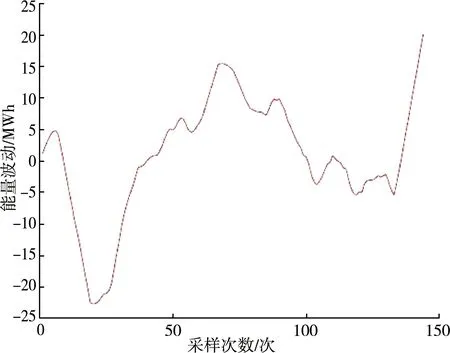
图9 第一天90%置信度的ESS系统出力的能量波动图
由图可知,90%置信度时ESS能量的波动变小,提升了储能设备的运行稳定性,减少运行费用。
比较全补偿和90%置信度下的ESS输出功率最大值和额定容量,如表3所示。

表3 不同置信度下的额定功率和额定容量对比
由表3可知,置信度越小,所需ESS额定容量就越小,在一定程度上得到降低了预测误差成本,既可达到电网对风电的消纳作用,又可获得合理的经济效益。
3 结 论
本文通过提出的基于风电预测数据的非参数核密度估计的方法来计算ESS额定功率和容量,求出上下分位点,优化ESS系统的输出功率数据,进而确定ESS系统的额定容量,风电场预测功率的精确性和ESS额定容量配置的合理性得到了提高,结合算例分析证明了此方法的可行性。
由于本方法仅使用历史风电数据,未考虑到气象因素对风电区间预测的影响以及电池储能系统的充放电效率及损耗问题无法量化,故估算结果存在一定误差。

