基于虚拟仪器的振动台迭代学习系统设计
安 欣,高 峰,杨巧玉,杨学山
(1.中国地震局工程力学研究所,中国地震局地震工程与工程振动重点实验室,黑龙江哈尔滨 150080;2.哈尔滨理工大学,测控技术与仪器黑龙江省高校重点实验室,黑龙江哈尔滨 150080)
0 引言
电动式振动台[1-2]一般用于仪器校准、结构振动测试、地震波复现等领域。在测试过程中,不仅需要以正弦波信号作为激励源,还要还原地震波信号。这就对振动台自身性能有较高的要求,一般地震波频谱覆盖范围是0~90 Hz,而台面带宽在开环状态下一般为1.5~50 Hz。通常增加速度、位移、加速度反馈构成闭环控制增加带宽[3-5],也有一些智能控制算法如滑膜控制、模糊控制、神经网络等也一定程度上改善台面波形复现效果。但随着台面载荷质量改变、导轨摩擦力、隔振等外部因素影响,也一定程度改变振动台自身参数及频响特性。
迭代学习控制(iterative learning control,ILC),是一种不依赖于系统模型的控制算法,用于可重复运动的控制系统中,通过迭代学习律改变输入信号以达到跟踪期望信号的目的[6],是一种智能控制算法,由Uchiyama提出,1984年,S.Arimoto等人提出PID型迭代学习律[7-8]。至此迭代学习算法被广泛应用于可重复运动系统中[9-11]。
在振动台测试研究中,测试仪器多采用信号发生器及数采卡配套采集软件,采集数据后通过数值计算软件分析结果后再重复此过程。测试过程繁琐,自动化程度低,在做重复性实验时,需要试验完成后一段时间才能给出。针对上述问题,本文采用虚拟仪器技术开发振动台专用迭代学习控制系统,达到针对特定环境、载荷、隔振等外部因素快速复现振动台波形的目的。同时,实时显示采集波形信号、分析波形频谱、保存实验数据、生成实验报告等功能。迭代过程完全自动无需专业人员值守,并自动分析迭代结果,如产生大幅扰动或迭代到达预期阈值能够自动停止。
1 测试系统总体方案
电动式标准振动台通过激励电压信号在电磁线圈中产生磁场力驱动台面做切割磁感线圈运动。所以需要将复现波形加速度电压信号作为驱动信号输入给放大器中,输出信号驱动振动台激振器。
图1为振动台迭代学习系统总框图,根据原始信号生成驱动信号,将驱动信号通过数据采集卡PXI-6281输出给功率放大器中,之后控制振动台做加速度往返运动复现波形,台面安置941B加速度传感器采集加速度信号,通过数据采集卡返回给虚拟仪器控制系统。

图1 振动台系统原理框图
图2为软件系统内部算法原理图,内置地震波形数据并保存于程序目录下。信号通过逆系统再经过迭代学习律生成新驱动信号,可做归一处理、比例变换、补充零点功能,之后发送数采卡,从数采卡采集波形也可做以上运算,并显示实时波形和加窗频谱曲线。通过与原始波形的相关分析,判定波形复现精度,如果相关度在逐步提高并没有达到目标值邻域,则继续迭代计算,再次生成新的驱动信号继续迭代。如果达到相关系数不再提高和达到设定阈值邻域之一则停止迭代,生成报告并输出。
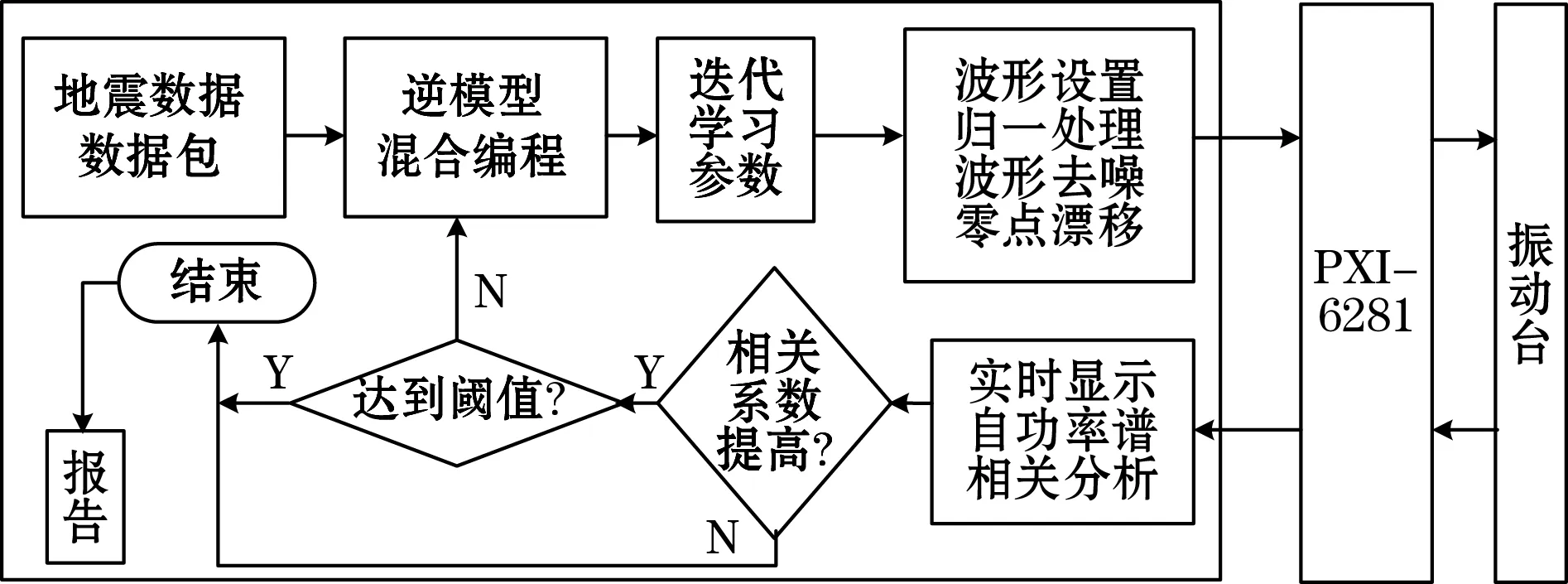
图2 迭代学习控制算法内部原理
2 振动台模型构建
2.1 振动台模型
图3为中国地震局工程力学研究所电动式地震标准振动台,台面载荷即传感器。激振器内有动圈。外加电压转换成电流产生磁场控制振动台运动。

图3 电动式地震标准振动水平台
图4(a)为力学模型,图4(b)为电器模型。模型中:u为输入电压信号;I为输入电流;M为台面质量;k为弹簧刚度;C为阻尼系数;x为台面位移;F为激振器推力;R0为动圈内阻;L0为动圈电感;G0为机电耦合系数,则线圈的感应电动势为G0sx,其中s为拉氏变换算子。
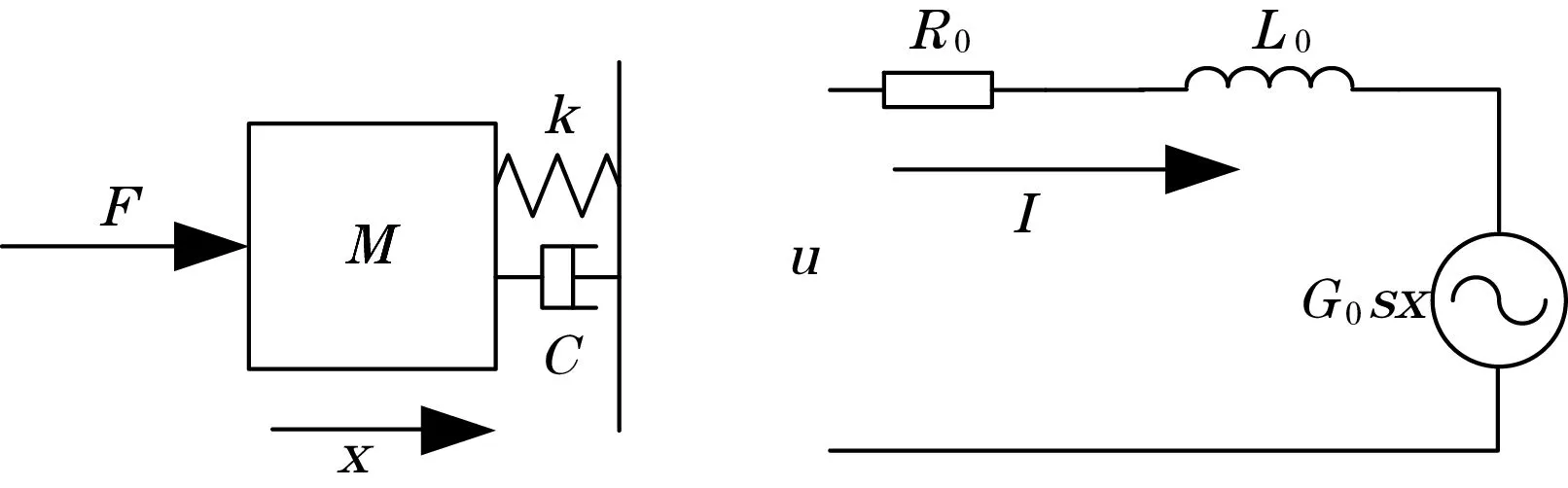
(a) (b)图4 振动台等效模型
可列方程:
(1)
式中:e为线圈激励电压;K0为放大器的比例系数。
式(1)中整理得到图5传递函数方框图。

图5 传递函数方框图
即:
(2)
2.2 系统逆模型建立
系统幅频响应曲线见图6,振动台加速度频谱曲线通频带在一定区间内。相频特性对本文结果影响不大,所以不做讨论。

图6 振动台传递函数
由于系统的低频与高频特性造成信号衰减。在系统中加入了逆系统模型以补偿频率特性,即:
G(s)-1G(s)=1
(3)
G(s)-1与系统本身传递函数互补。如图7所示。

图7 逆系统传递函数
3 软件系统设计
虚拟仪器开发速度快,本身数据采集功能强大,适用于本文所述环境。在逆函数运算部分LabVIEW处理能力有限,因此采用MATLAB处理传递函数、逆函数的构建、曲线拟合及驱动信号反演,与LabVIEW混合编程。
软件构造如图8,首先程序初始化波形保存格式、迭代参数、波形整定参数、采样率、采样方式等数据。数采卡同步发出和采集波形,通过放大器发送给振动台,台面加速度通过941B传感器返回给AI(模拟信号输入)接口。采样率为每秒钟采集200点。地震波信号首先通过LabVIEW与MATLAB混合编程的逆函数模块,生成驱动信号,之后输出给放大器。信号采集过程中实时显示采集的波形并显示。采集完成后自动保存到指定文件夹同时加载数据并分析与期望信号的相关系数,得到波形复现精度,同时也对自功率谱做同样的分析。
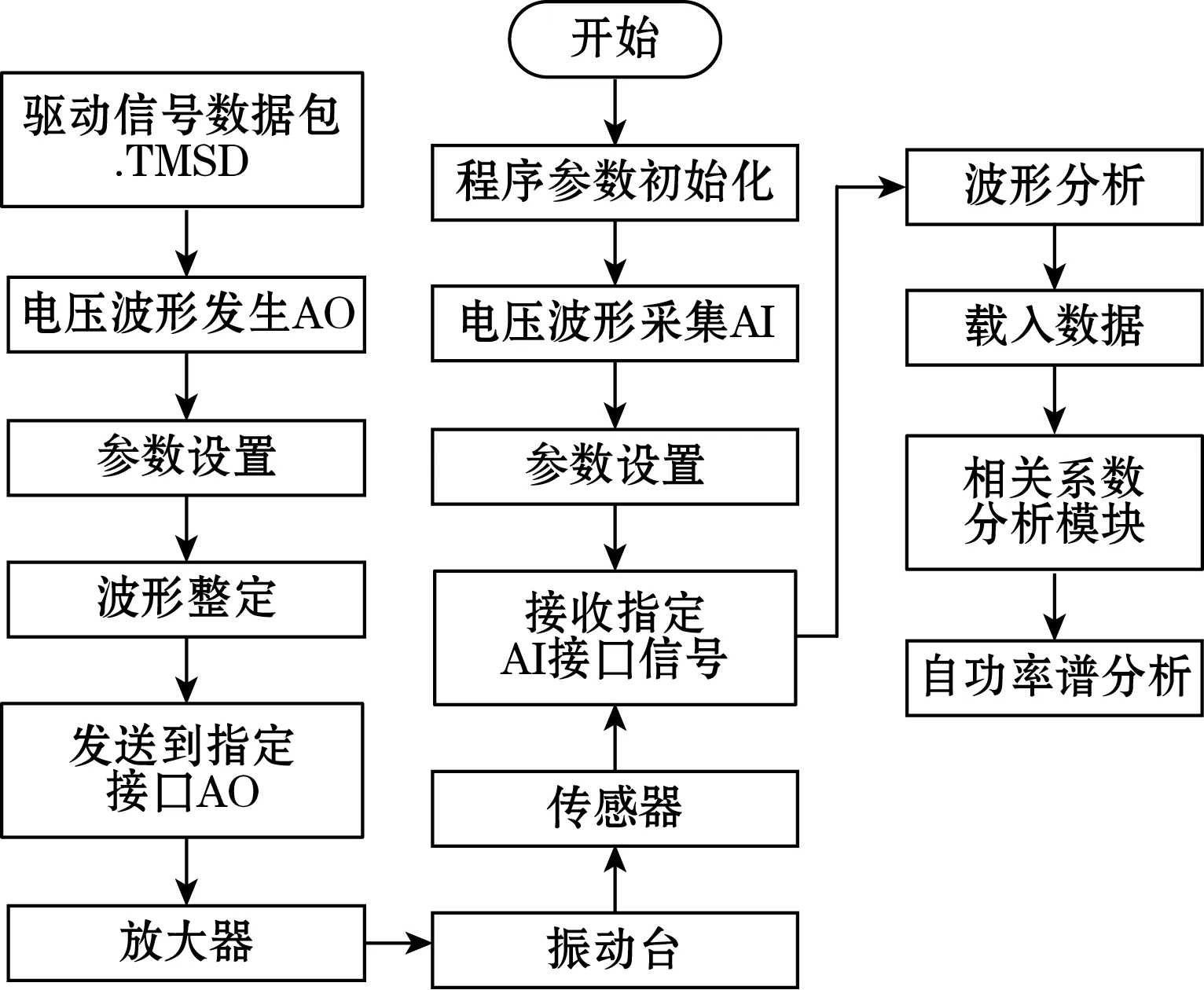
图8 软件整体框图
3.1 相关系数模块
相关系数可作为评价台面波形与期望波形相似程度的一种技术指标。相关系数是研究变量之间线性相关程度的量,是无量纲的量。当2个随机变量X和Y是相互独立的,如用X的线性表达式aX+b与Y比较,求得均方误差为
e=E[(Y-(a+bX))2]
=E(Y2)+b2E(X2)+a2-2bE(XY)+2abE(X)-2aE(Y)
(4)
式中E(X)为X的期望。
对两者均方误差展开后得到式(4),两者误差越小则越相近。因此,改变变量a、b的值,使均方误差e达到最小即可:
(5)
设X和Y协方差表达式为
Cov(X,Y)=E{[X-E(X)][Y-E(Y)]}
(6)
(7)
式中D(x)为方差。
将此时的a、b的值带回到式(4)中,得到此时均方误差最小值为
(8)

|ρXY|∈[0,1],能够很好表达X、Y近似程度,为1则表示X、Y完全一致。如果ρXY=-1则表示两波形完全一致但相位相反。
系统旨在复现地震波信号,所以利用相关系数来评判复现波形与原始数据的一致程度。为了防止延迟等因素造成采集数据与原始数据的数据长度不一致,而相关系数在计算过程中必须保证X、Y的数据长度一致,否则无法计算。因此,需要对采集波形做对齐处理。
由式(7)、式(8)可知,当两随机数据均方误差最小时,相关系数最大。设Y的数据长度为N,X的数据长度为M。在X上取与Y长度相等一段Xn(n∶n+N),n为起始点位置,n+N为经过数据长度后的终止点位置;将每个Xn与Y进行相关系数分析得数组ρn,其中maxρn为X,Y均方误差最小点,两波形相似度最高,表明波形对齐。
图9为相关系数计算模块,为系统子VI,包括2个输入端,即2路波形文件地址(TDMS格式);5个输出端,即相关系数、自功率谱相关系数、2路波形显示和程序运行进度条,同时输出对齐波形方便调用。图10为对齐后两波形状态,其相关系数为0.87。

图10 利用相关系数对齐波形效果图
3.2 前馈补偿模块
式(3)提到过前馈补偿器的设计,在对振动台传递函数求逆以及振动台波形反演逆推驱动信号过程中涉及到大量矩阵运算。本文选用MATLAB函数计算引擎完成该部分功能,在计算机中安装MATLAB计算引擎,在LabVIEW程序中加入MATLAB script节点,将程序写入其中并引出交互变量data和datan作为模块输入输出。如图11所示
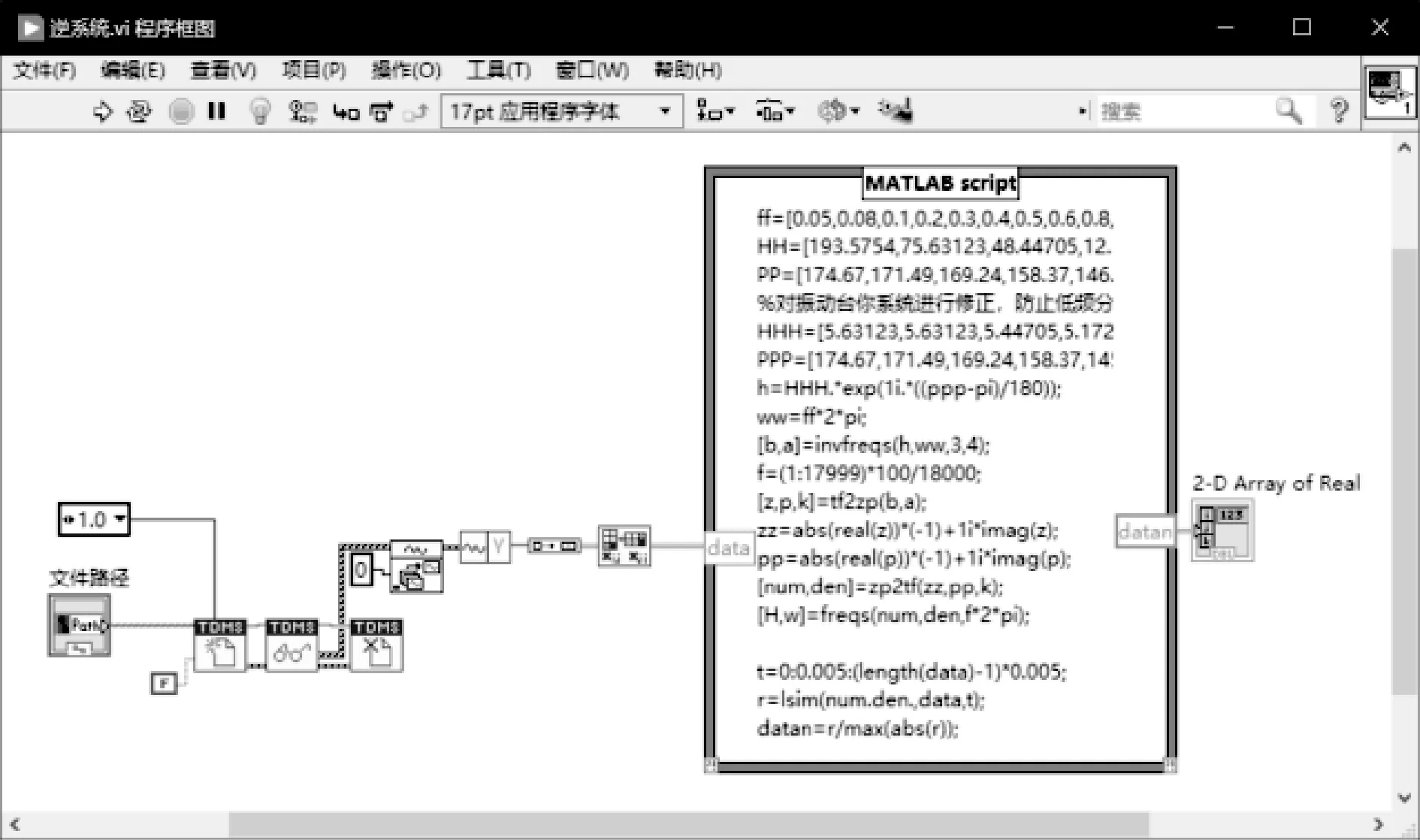
图11 前馈补偿模块
函数首先调用波形文件,将波形文件中波形数据转置后输入MATLAB script节点,在MATLAB script节点函数中建立系统逆模型,并修改模型低频特性参数,将波形反演求出振动台驱动信号。
3.3 迭代学习算法
迭代学习控制能将可重复运行系统经过多次循环控制,完成将被控量接近期望量的一种智能算法。如图12所示。
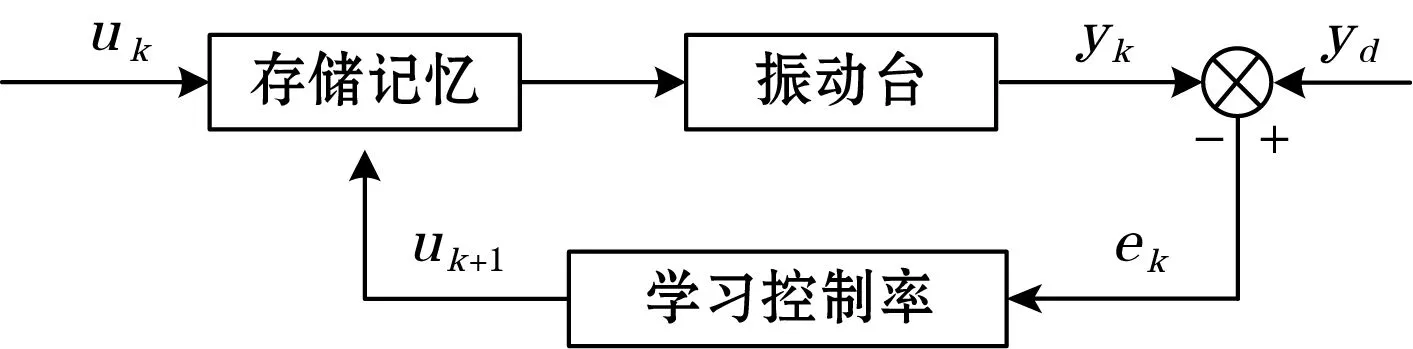
图12 迭代学习算法示意图
uk为系统第k次迭代的驱动信号,yd为输出信号,yk为期望信号,ek为误差信号,ek=yd-yk。迭代学习算法是利用某种控制律将驱动信号与误差信号联系起来,推导出新的驱动信号uk+1。理论上,当迭代次数无限增大时,误差趋近于0,而实际中,由于系统本身存在噪声、扰动等因素,迭代只能收敛于期望信号附近,不能完全跟踪。
在理论上,如果k趋向于无穷时,ek趋近于0,则说明迭代控制是收敛的。然而在实际应用中,系统本身存在状态扰动、测量噪声、输入扰动等干扰,迭代系统会收敛到期望轨迹的邻域内。常见的学习律有D型、P型、PI型、PD型等。以上几种均可视作PID型迭代学习算法比例、积分、微分系数取零的特例。因此,系统在算法设计中直接采用PID型迭代学习算法,在此基础上加入遗忘因子,即本次迭代过程按百分比遗忘上次迭代数据并混入初次迭代信号,当系统受到大幅扰动影响时,该部分可减小扰动造成的影响。
(10)
式中:r为收缩因子;Γ为微分项系数;L为比例项系数;Ψ为积分项系数:
图13为软件的主界面,主要分为2部分,一部分为波形及迭代次数信息显示卡,如图13左侧,该部分显示系统工作状态、迭代时长、迭代次数等信息,如不采用迭代控制算法,则软件可单纯实现数采功能。右侧为5个选项卡,分别为参数设置、结果显示、AI输入波形、AO输出波形及说明文件。该部分对系统信息进行详细设计,同时可以实时观测采集波形状态。
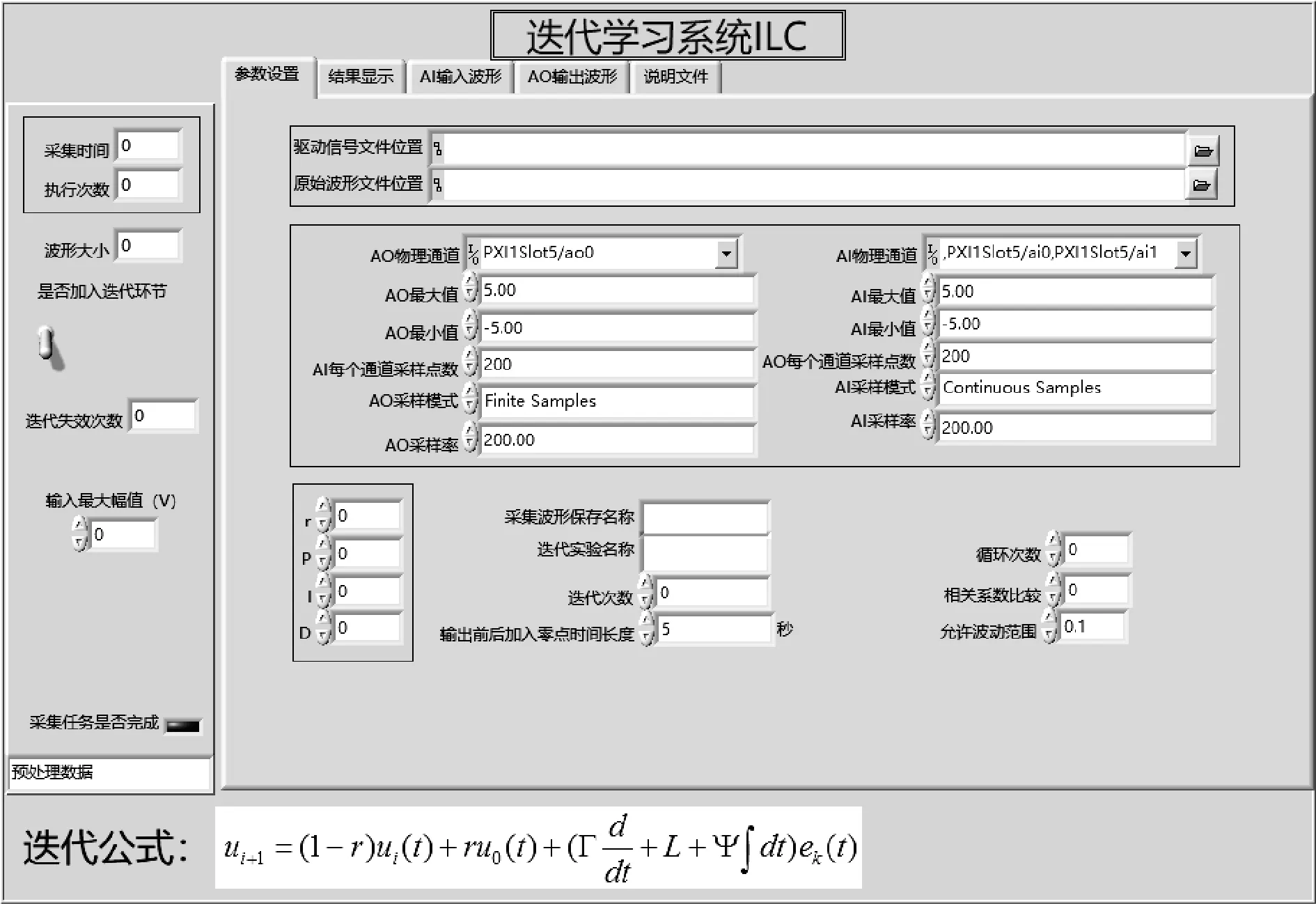
图13 迭代学习控制系统首页
迭代循环结束后,自动判别迭代效果,如果相关系数比前次有所提升,则自动把本次计算结果及参数填写到表格中并将波形数据以迭代名保存。本次迭代结束后迭代次数自动加1,继续下次迭代直到达到指定期望值或指定迭代次数后停止。
在测试过程中会遇到外界干扰、断电、改变参数等因素影响造成本次迭代效果无效的情况。软件加入对此类问题的判别程序,如相关系数大幅降低,则询问并取消本次结果并重新开始本次迭代。
4 实验结果
选取广元石井东西向地震波测试系统功能。遗忘因子r为0.28;比例系数为0.1;微分系数为1.79;积分系数为0.1,测试结果如表1所示。

表1 广元石井迭代数据
将表1中数据绘制成图14,振动台复现随迭代次数增加而增加,到达0.97附近时相关系数提升效果不明显,波形复现效果收敛到该值附近。而自功率谱一直处于较高复现精度,表明波形复现度增加后,对频谱成分影响不大。

图14 广元石井迭代曲线
5 结束语
本文利用虚拟仪器在振动台上完成迭代学习系统设计,通过迭代学习控制算法,实现振动台波形复现。只需简单设置即可自动迭代完成波形复现,减轻测试人员工作强度,同时,高精度的复现波形可在仪器校准、结构测试中提供有力的技术保证。系统加入了遗忘因子、比例积分微分系数等参数,能使科研人员灵活设计迭代过程及参数。

