基于涡致振动的T型悬臂梁压电俘能结构的仿真与实验研究
李 莉,林杉杉,王 军,王永耀,于慧慧
(1.沈阳化工大学计算机科学与技术学院,辽宁沈阳 110142;2.辽宁省化工过程工业智能化技术重点实验室,辽宁沈阳 110142;3.北京信息科技大学传感技术研究中心,北京 100631)
0 引言
近年来,微机电系统设备和微传感器等低能耗的电子产品发展迅速,在各个领域均有广泛的应用。目前这些微型电子设备的供能大多是传统的化学电池,由于传统电池具有质量大、容量有限,更换困难且污染环境等缺点,因此将自然环境中的能源转化为电源,从而为器件提供稳定长期的供能尤为重要。常见的自然能源收集方式有太阳能、振动能、热能、电磁能等[1-2]。其中振动能收集通常是采用压电材料将振动产生的机械能转化为电能,这种压电式振动能量收集由于收集装置结构简单、易于制作、无热效应等优点在振动能量收集技术方面具有广阔的发展前景[3-4]。
自2001年G. W. Taylor[5]等证实了基于涡致振动能量收集的可行性以来,国内外的研究人员对风产生的涡致振动进行能量收集做了一些研究[6-9]。S. M. Yun[10]等提出了利用阻流体、压电悬臂梁及固定底板组成的压电能量收集装置,并在风洞中进行了实验,研究结果表明该装置可产生1.9 V的电压。丁林[11]等提出柱体下端为自由端,上端与压电片连接,压电片上部固定于风洞测试段顶面的压电能量收集装置,研究结果表明钝体为方柱时,其振幅、输出电压和功率最大分别为0.15 m、0.55 V和0.378 μW。W. Sun[12]等对压电悬臂梁前置阻流体进行了实验研究,研究结果表明,阻流体形状为球茎形截面为最佳,产生最大电压为5.5 V。成立[13]等设计了一种利用风能驱动多压电片振动发电的装置,该装置通过风能驱动叶轮旋转迫使压电片振动从而产生电能,研究结果显示该装置经过30 min的工作,产生的电能可以供1 W的节能灯持续工作50 s。虽然现有的研究结果已经证明了风中涡致振动能量收集技术的可行性,但与目前常用的风力涡轮机相比,在收集效率、发电能力、能量密度等方面仍处于劣势,因此研究和优化压电俘能结构,对提高风中涡致振动能量收集技术有着重要的意义。
本文对前置阻流体的T型悬臂梁压电俘能结构进行了数值仿真及风洞实验,通过分析风速、前置阻流体参数以及阻流体与压电能量收集结构之间的间距,确定T型悬臂梁压电俘能结构发电的最佳参数,为基于涡致振动的压电俘能装置的设计及优化提供理论和实验参考。
1 数学建模
T型悬臂梁式压电俘能结构如图1所示,中间铜片作为基板,压电陶瓷附着在铜基板的两侧,底端为T型,以便于固定,上端自由。该压电俘能结构尺寸微小,结构简单,易于固定,谐振频率低,压电片并联双晶结构发电效率高,输出电流大。
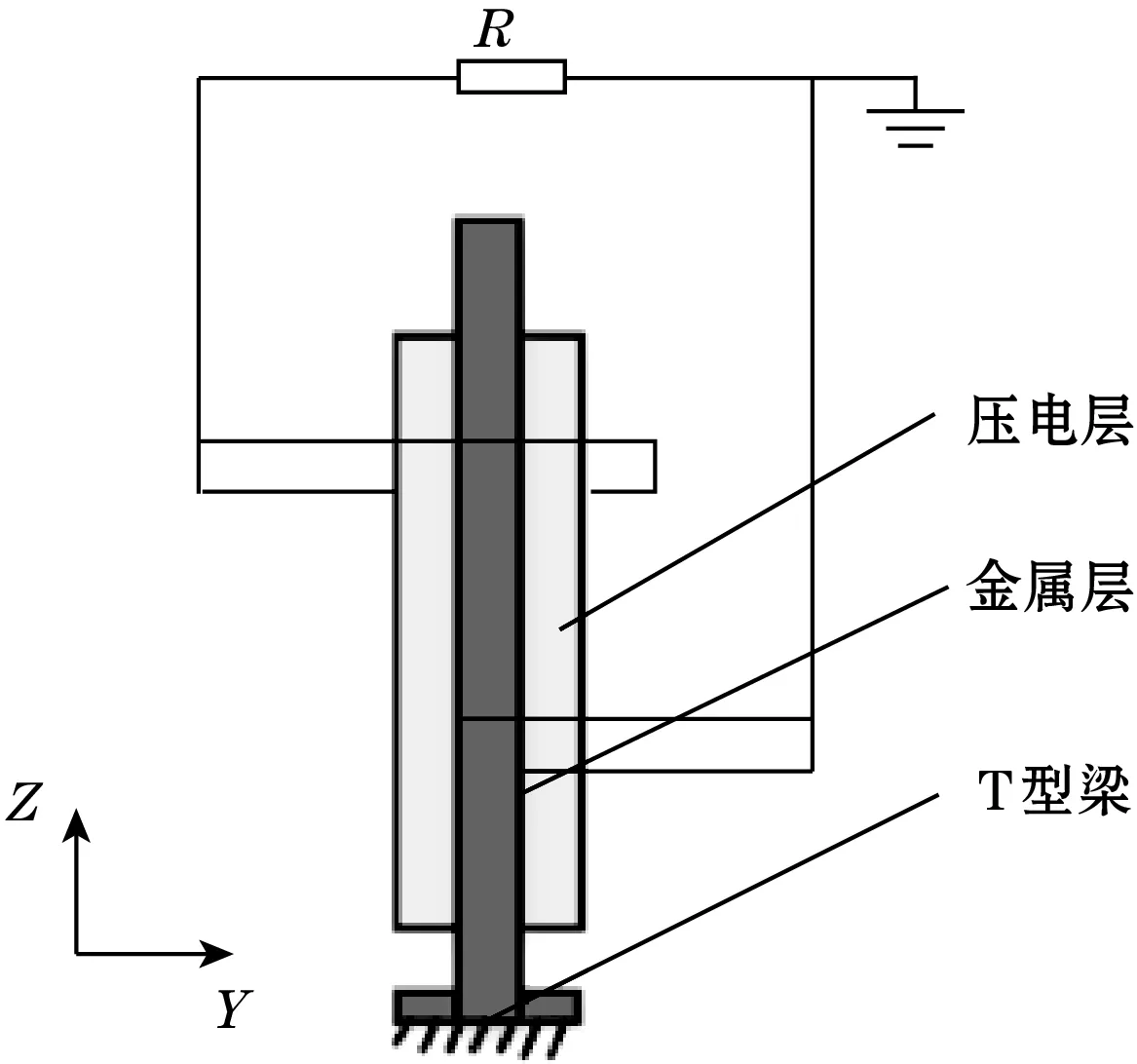
图1 T型悬臂梁结构图
流体流动控制方程即N-S方程为:
(1)

式(1)为流体的速度场提供了解决方案,即流体施加在固体上的力等于流体反作用力[6],计算公式如下:
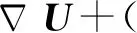
(2)
式中:n为流体边界外法线单位向量;p为压力;I为单位矩阵;μ为动力粘度。
T型悬臂梁压电俘能结构置于阻流体后方,使用任意拉格朗日-欧拉法描述流体力学与固体力学的耦合作用,由于流固耦合作用,在阻流体尾迹处,俘能结构受到阻流体尾迹旋涡的作用,在垂直于来流方向,即Y方向产生规律的弯曲振动,从而迫使双晶压电片产生形变,进而在其两端产生电位差。由于旋涡的作用,使得压电俘能结构在垂直来流方向的横向振幅远大于顺流方向的振幅,因此在顺流方向的振幅可以忽略不计,根据欧拉-伯努力梁理论,压电悬臂梁产生力和力矩的平衡方程为
(3)
式中:M(x,t)为由于机械应变产生的力矩;m为俘能结构单位长度的质量;w(x,t)为俘能结构的挠度;p(x,t)为任一点x的时间压强函数。
压电材料的压电方程为
(4)
式中:D3为电位移;εT为介电常数;E为电场强度;d为压电系数;T为应力,下标3代表3轴方向;S为应变;SE为柔顺系数,其值为弹性模量的倒数,下标33表示压电材料的受力方向和极化方向均为3轴方向。
结合式(3)和式(4)得T型悬臂梁的运动方程为
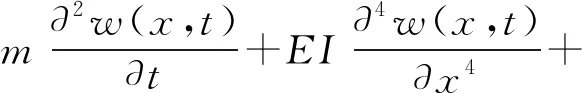
(5)
式中:θ为T型悬臂梁的机电耦合系数;V(t)为电压随时间变化的函数;δ(x)为任一点x的坐标函数;δ(x-L)为x点至结构顶端的距离函数。
则由运动产生的电方程为
(6)
式中:q(t)为应变耦合与内壁电场位移的电荷之和;C0=4.5×10-8F为T型悬臂梁内部等效电容。
则得到的电流为
(7)
由欧姆定律得:
(8)
式中:R为等效电阻。
由于C0的值较小,在计算时可以忽略该项,因此式(8)可简写为
(9)
由式(9)可以求出T型悬臂梁上某一点任意时刻的电压值,由于N-S方程求解困难,不能通过计算求得解析解,因此基于以上数学模型,利用计算机仿真对俘能结构在风中的涡致振动进行流固耦合和压电耦合仿真。
2 数值仿真及实验设计
2.1 数值仿真设计
根据上面提出的数学模型,在ADINA软件中对风中涡致振动的T型悬臂梁压电俘能结构进行仿真建模,如图2所示。仿真模型原点位于上游阻流体的中心处,X轴为流体来流方向,U为风速,阻流体与入口处的距离A为0.05 m,Z轴沿阻流体垂直向上,Y轴垂直于X-Z面,T型悬臂梁压电俘能结构沿来流方向放置于阻流体后,两者中心距离为L,悬臂梁主平面平行于来流方向,阻流体与压电悬臂梁均为底端固定,上端自由,为了提高计算精度,阻流体及俘能结构周围的网格划分较密集。
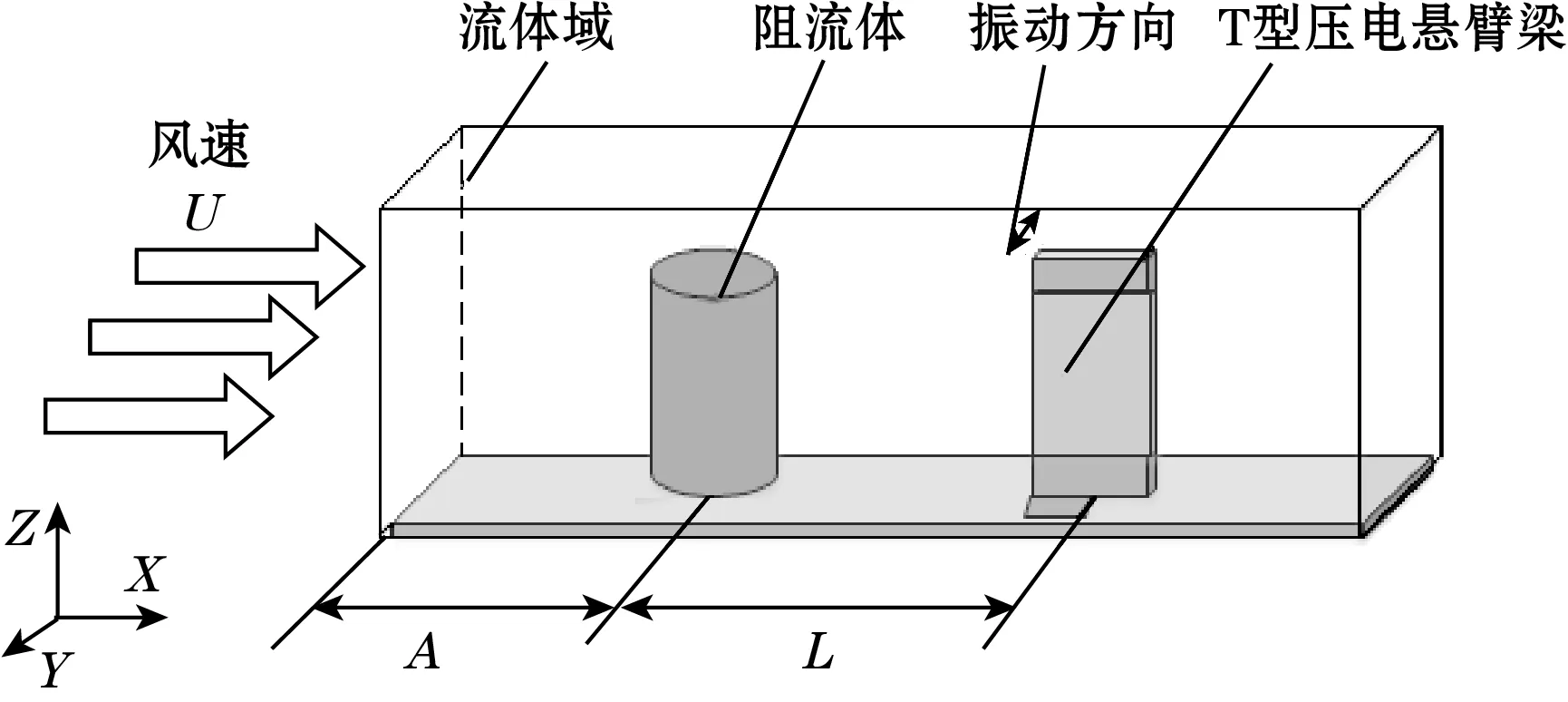
图2 三维结构图
对上述模型进行流固耦合计算,选取t=3.984~4.014 s范围时,每隔0.04 s的涡致振动作用情况如图3(a)~图3(d)所示。
由图3可得,在选取的时间段内,前置圆柱阻流体的后方产生了周期脱落的旋涡,脱落的旋涡作用在俘能结构上,使俘能结构在Y方向产生规律的振动,与理论分析结果一致,证明了T型悬臂梁压电俘能结构在风中涡致振动的可行性,此时T型悬臂梁压电俘能结构产生的振幅随时间变化的曲线如图4所示。
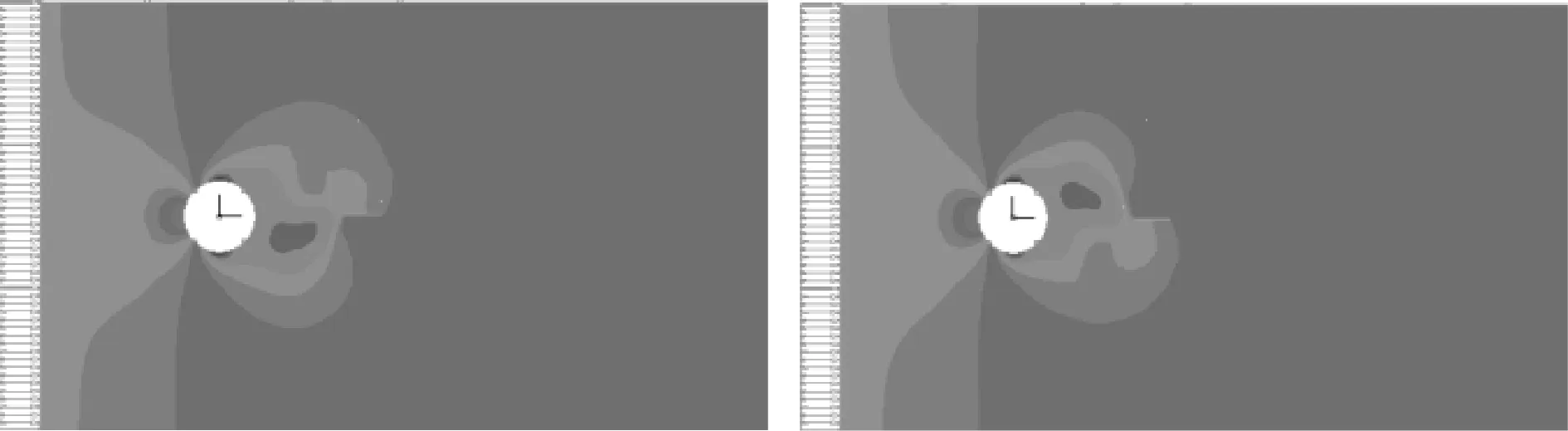
(a)t=3.984 s (b)t=4.024 s

(c)t=4.064 s (d)t=4.104 s图3 不同时刻涡致振动作用图
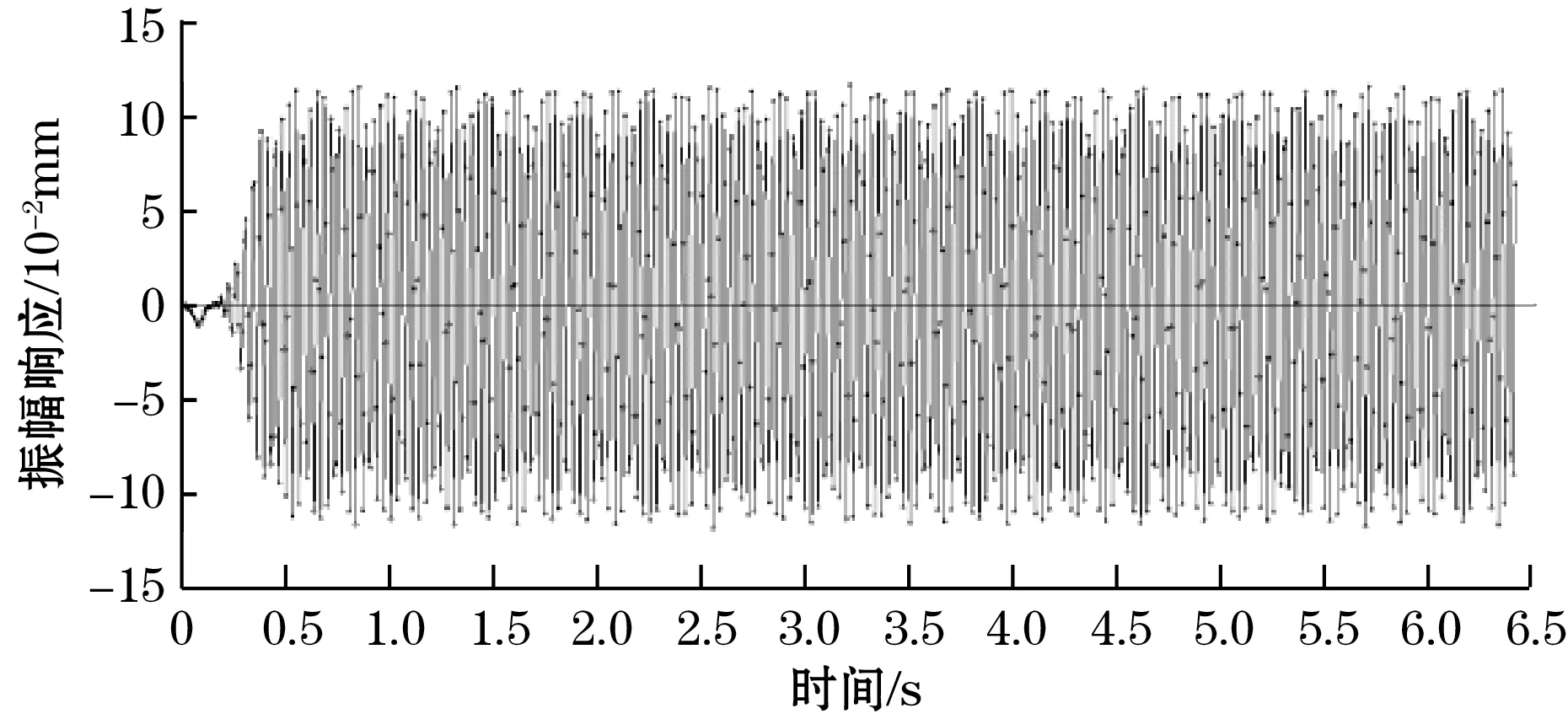
图4 振幅-时间曲线图
从图4中可以看出,T型悬臂梁在风中涡致振动的作用下,产生了周期性的振动,振动曲线为正弦曲线,这种振动可驱动T型悬臂梁产生规律的电压,将此电能进行收集即可为需要供能的器件提供稳定的电能。
2.2 实验系统设计
基于涡致振动的T型悬臂梁压电俘能结构的实验在如图5所示的风洞中进行。风洞为直径0.315 m的圆筒形,总长2 m,风机选用轴流式风机,使用风速调节器对风速进行调节;在风洞底部设置固定支架,用来固定阻流体及俘能结构,固定支架上标有刻度以确定结构的位置;在风洞出口处设置风速仪(0~45 m·s-1)实时监测风洞中风速的变化情况;数字示波器与计算机连接,实时观测输出电压。T型悬臂梁压电俘能结构的具体参数如表1所示。
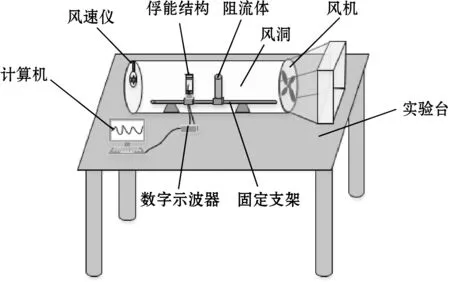
图5 实验装置图
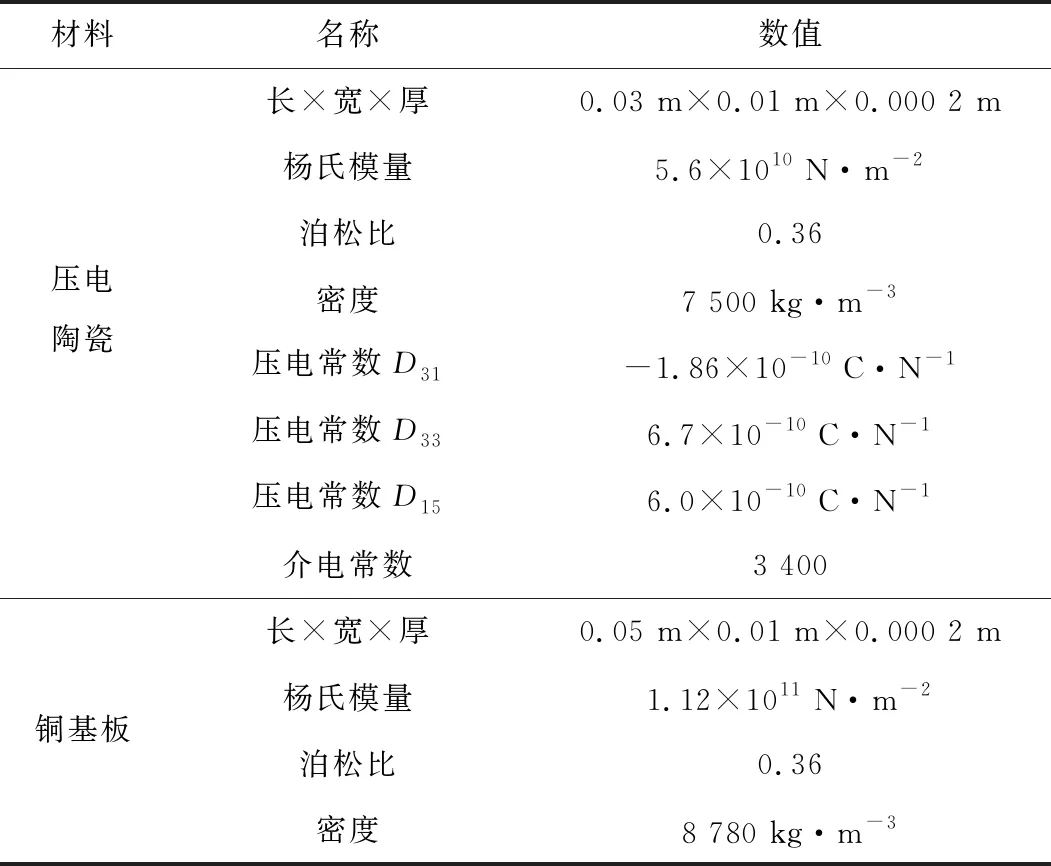
表1 T型悬臂梁压电俘能结构参数表
根据文献[14],存在一个最优负载,可使俘能结构输出功率最大,最优负载电阻的表达式为[15]
(10)
式中f为固有频率。
由式(10)可知,俘能结构的最优负载只与结构本身的固有频率及内部电容有关,由于俘能结构的固有频率是确定的,最优负载电阻也随之确定,将表1中的参数代入式(10),得最优负载电阻为1 MΩ,因此本实验中均串联1 MΩ的负载电阻进行测试。
3 结果与分析
3.1 阻流体形状对俘能结构性能的影响
本文选取风速为0~6.5 m·s-1进行研究,当流体流经阻流体时,由于阻流体的形状和尺寸等参数不同,在阻流体两端产生的剪切力也不同,导致阻流体后方的旋涡强度不同。本文选取直径为0.02 m的圆柱,边长为0.02 m的四棱柱,对角为0.02 m的六棱柱,其高均为0.05 m的阻流体,后加俘能结构进行仿真及实验分析,阻流体与俘能结构之间的距离为0.04 m,得到的仿真电压值与实验电压值随风速的变化分别如图6(a)、图6(b)所示。
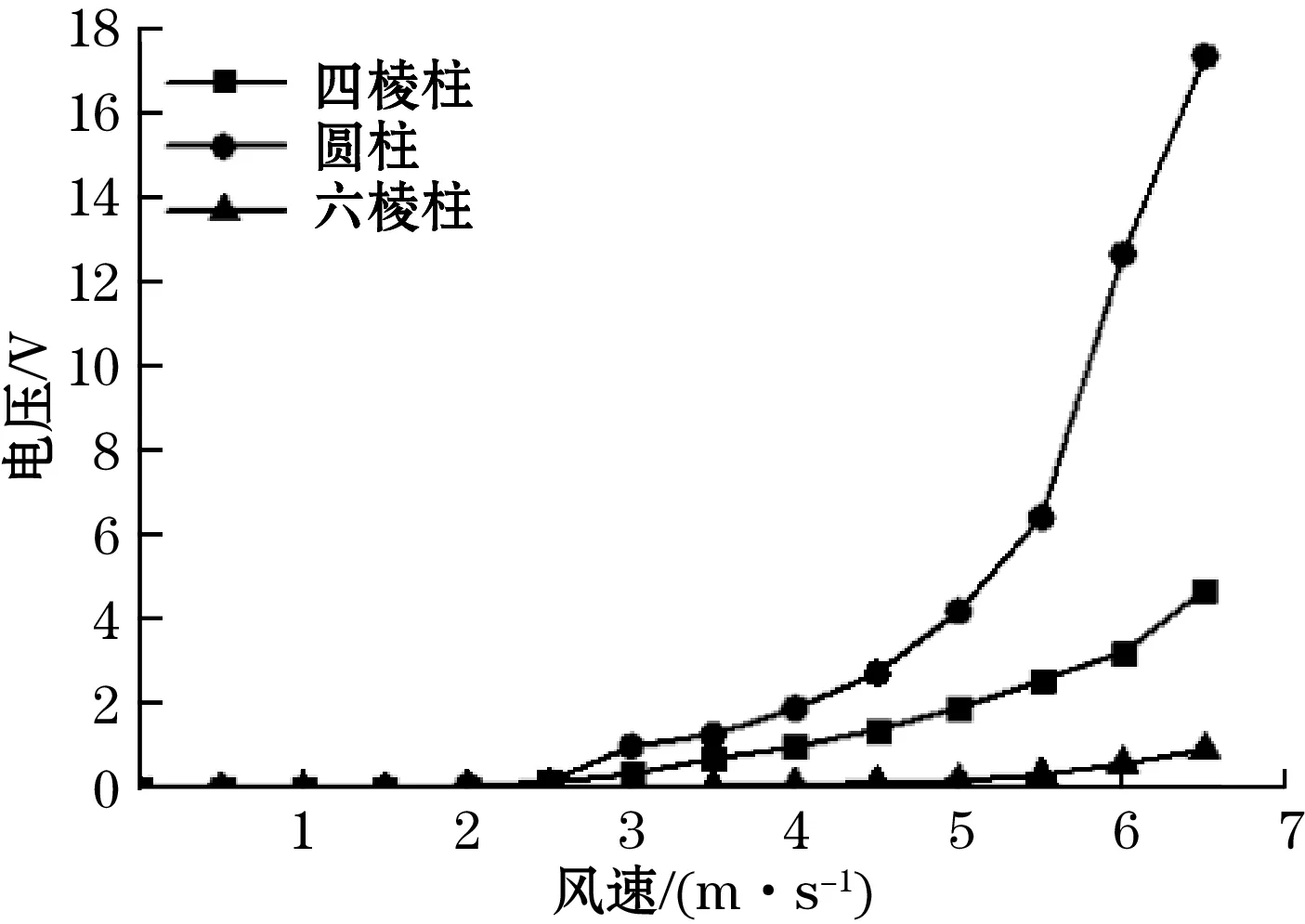
(a)仿真电压值
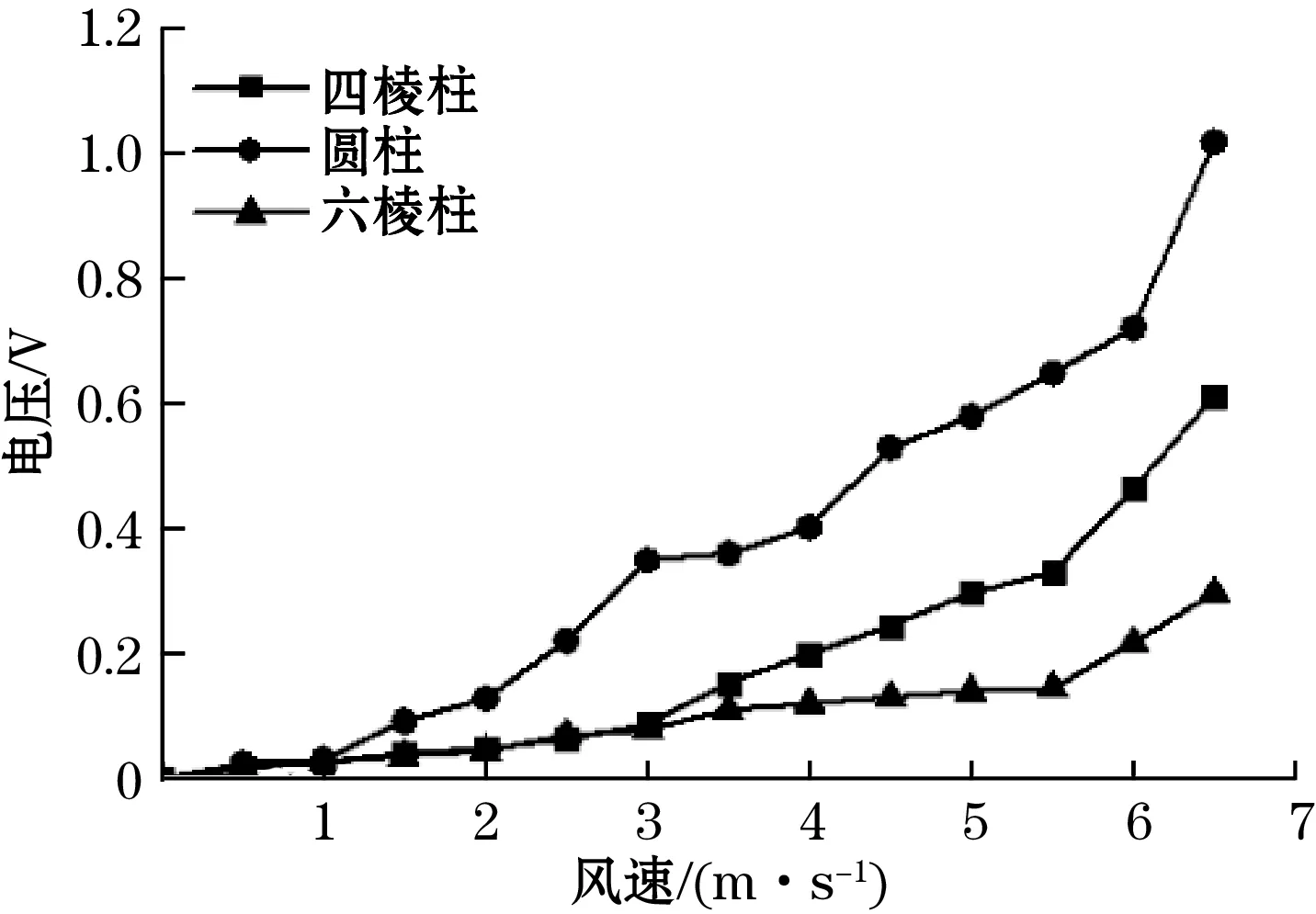
(b)实验电压值图6 不同形状阻流体电压随风速的变化图
由图6(a)、图6(b)可得,在测试风速0~6.5 m·s-1范围内,前置3种形状的阻流体,其仿真电压值与实验电压值呈现相同的变化趋势,均随着风速的增大而增大,证明了仿真与实验的正确性。由于在仿真过程中为了简化建模及计算过程,设置了假设条件,仿真情况为理想工况,而实验中由于串联电阻、热能散失、焊点的存在等原因导致电荷流失,使得实验值与仿真值相差较大。当来流风速较小时,空气的能量密度较低,此时后方的俘能结构输入能量与自身结构阻尼消耗的能量相差较小,因此未发生规律的振动,产生的电压也较小;随着风速的增大,空气的能量密度逐渐增大,俘能结构在阻流体尾部流场的作用下,输入能量远大于自身消耗的能量,此时振动幅度增大,产生的电压也随之增大。
相同风速下,例如当风速为6.5 m·s-1时,阻流体为圆柱时俘能结构产生的电压远大于阻流体为四棱柱以及六棱柱,阻流体为四棱柱时略大于六棱柱,这是由于棱柱有尖锐的棱边,流体流经阻流体时,在棱边处发生了多方向的边界层分离,产生的旋涡未能集中作用在后方的俘能结构上,而圆柱表面光滑,流体在其尾流处形成规律的旋涡作用在俘能结构上,使其产生更大的振动幅度,此时产生的电压也较大。综上分析,在测试范围内,T型悬臂梁压电俘能结构产生的电压随风速的增大而增大,与四棱柱和六棱柱相比,前置阻流体为圆柱时俘能结构产生的电压最大。
功率的计算公式为
(11)
式中V为俘能结构产生的电压值。
由式(11)可得输出功率随电压的增大而逐渐增大,即在实验测试范围内,输出功率均随风速的增大而增大,当风速为6.5 m·s-1,圆柱阻流体直径为0.02 m,高为0.05 m时,T型悬臂梁压电俘能结构的输出电压和输出功率最大,值为1.02 V、1.04 μW。
3.2 前置圆柱阻流体尺寸对俘能结构性能的影响
根据3.1节的分析,阻流体形状为圆柱时,T型悬臂梁压电俘能结构发电性能优于其他形状的阻流体,为了进一步分析阻流体参数的影响,选取直径D分别为0.01、0.02、0.03 m,高为0.05 m的圆柱,阻流体与T型悬臂梁压电俘能结构之间的间距与阻流体直径的比值(L/D)为2进行分析,得到电压随风速的变化如图7(a)、图7(b)所示。
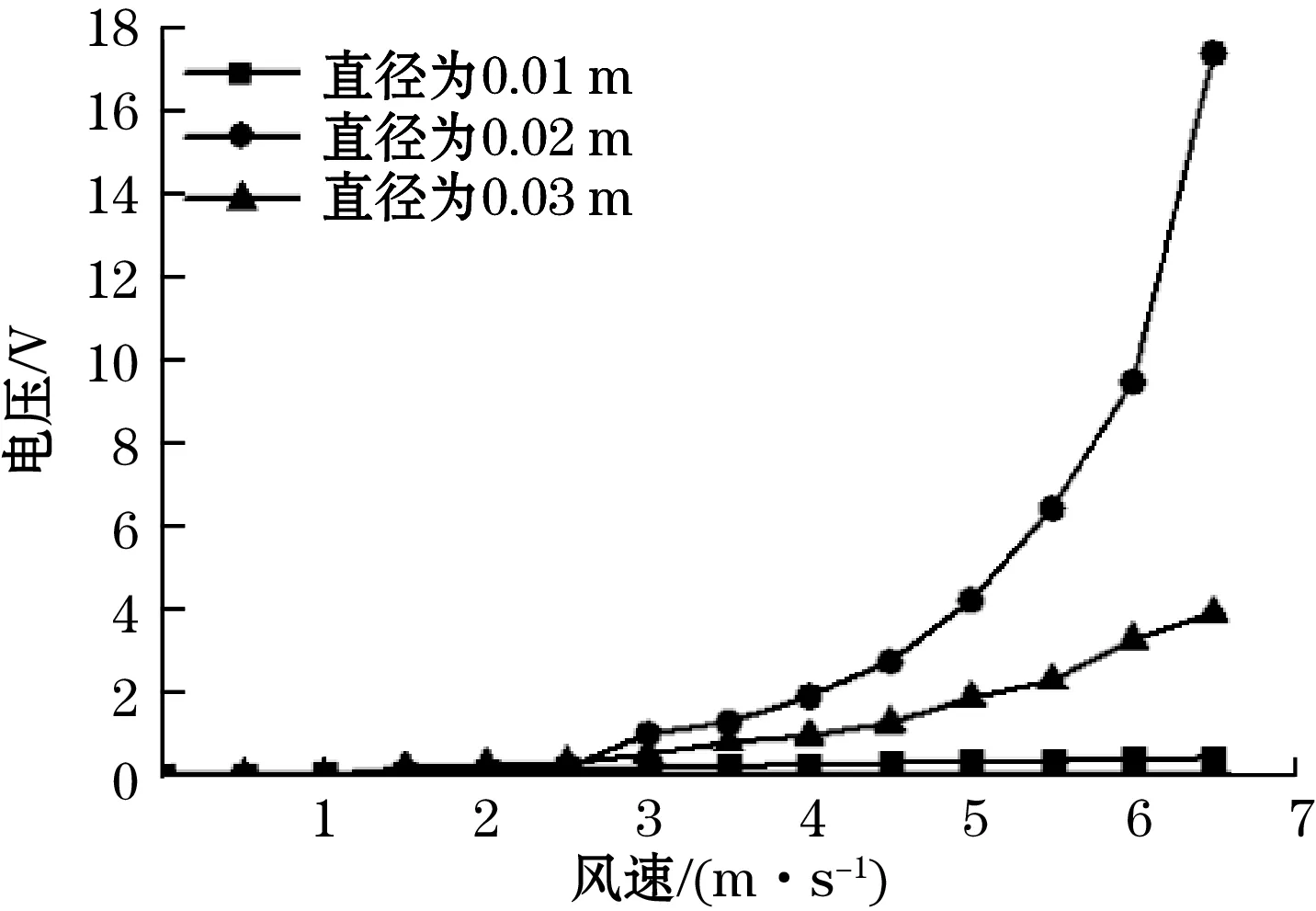
(a)仿真电压值

(b)实验电压值图7 不同阻流体直径电压随风速变化图
由图7可以看出,3种情况下,俘能结构产生的电压均随风速的增大而增大,与3.1节研究结果保持一致。同一风速下,当阻流体直径为0.02 m时,产生的电压均大于阻流体直径为0.01 m和0.03 m,阻流体直径为0.01、0.02、0.03 m时的实验输出功率分别为0.29、1.04、0.74 μW,因此阻流体直径为0.02 m,高为0.05 m的圆柱为最佳阻流体。
3.3 阻流体与T型悬臂梁的间距与直径比的影响
选取风速为6.5 m·s-1,阻流体直径为0.02 m,高为0.05 m,改变阻流体与T型悬臂梁压电俘能结构之间的间距进行仿真和实验分析,得到T型悬臂梁压电俘能结构的电压随阻流体和俘能结构之间间距与阻流体直径的比值(间距直径比L/D)的变化如图8(a)、图8(b)所示。
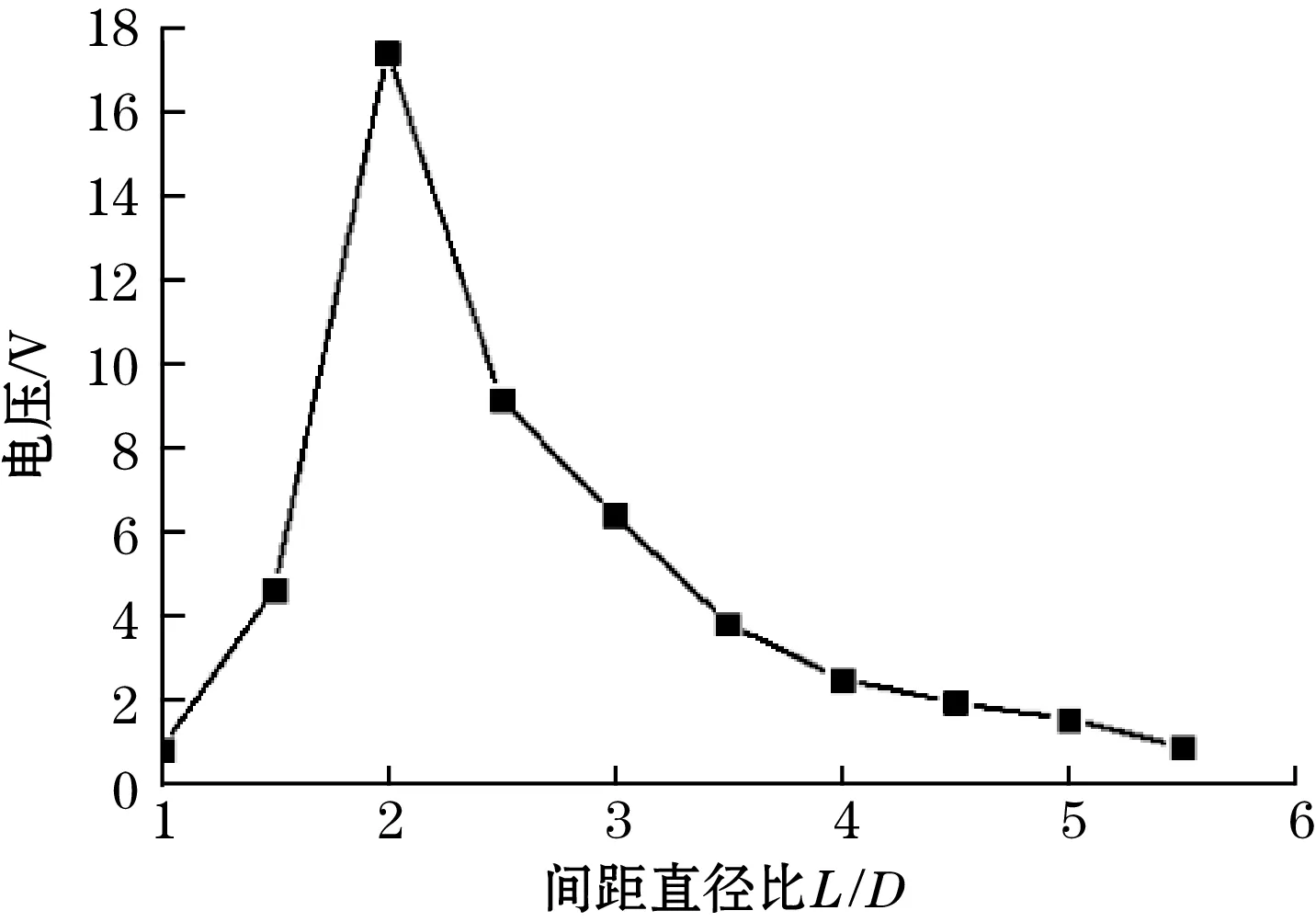
(a)仿真电压值
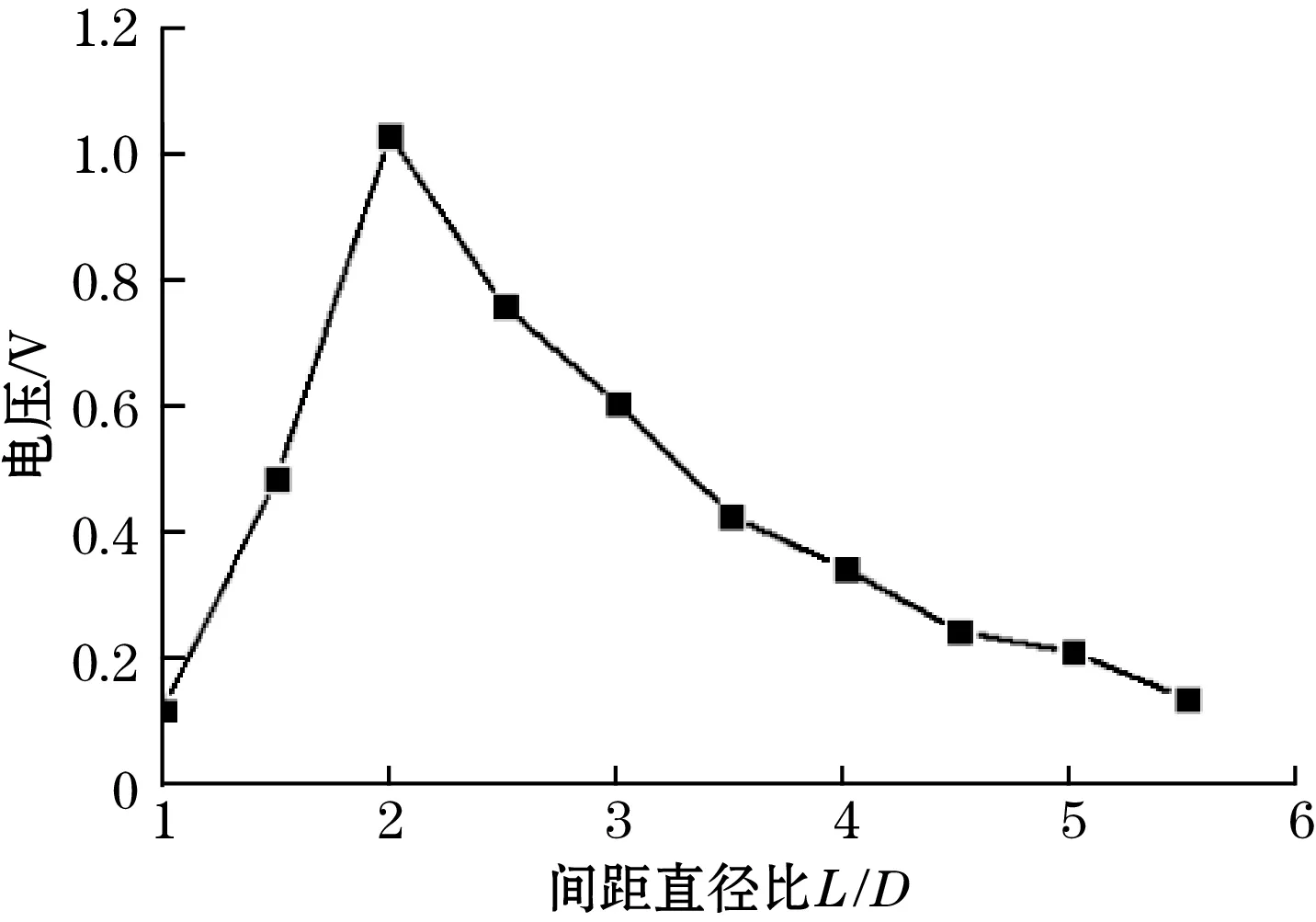
(b)实验电压值图8 不同间距直径比对电压的影响图
由图8可以看出,电压随着间距直径比的增加呈先增大后减小再逐渐不变的趋势。当间距直径比为2时,俘能结构产生电压值最大。以L/D=2和3.5为例,阻流体后方产生的旋涡对俘能结构的作用如图9(a)、图9(b)所示,当L/D较小(<1.5)时,两者可看作为一个整体,在阻流体后方形成完整旋涡之前流体就已经流过俘能结构,旋涡未能对其产生作用;当L/D适中(1.5~3)时,阻流体后方产生的旋涡完整的作用在俘能结构的侧面,使俘能结构受到的力较大,产生较大的形变,因此产生更大的电压;当L/D较大(>3)时,两者相当于2个独立的个体立于流体域中,阻流体后方形成的旋涡在到达俘能结构之前就已经消失,阻流体的尾流对其未产生明显的影响,此时T型悬臂梁的振动较小,产生的电压也较小。综上分析可得,阻流体与T型悬臂梁之间的间距直径比为2时,俘能结构的性能最优,实验测得电压为1.02 V。
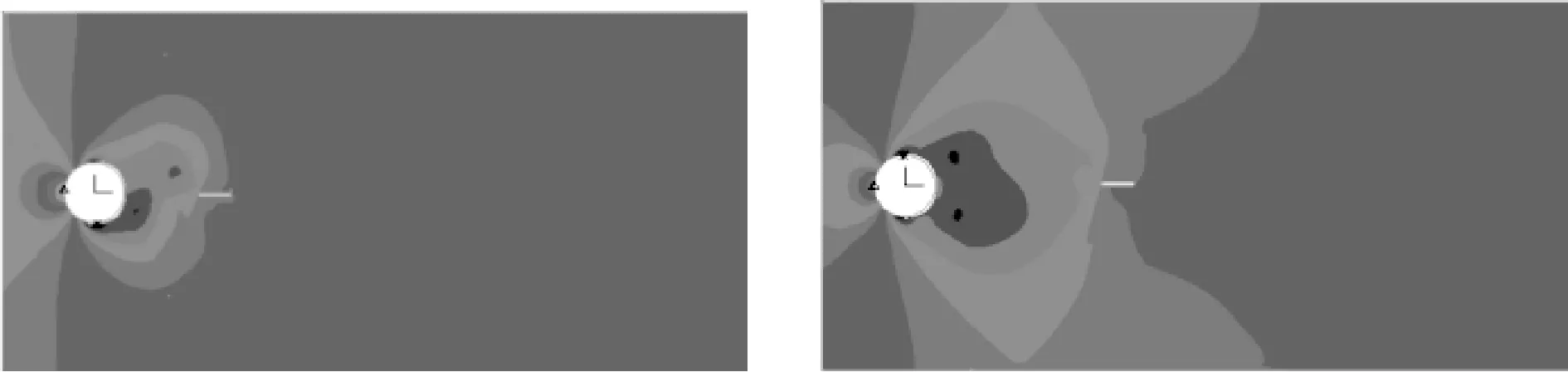
(a)L/D=2 (b)L/D=3.5图9 不同间距直径比涡致振动作用图
4 结束语
本文对基于涡致振动的T型悬臂梁压电俘能结构进行了数学建模,利用ADINA仿真软件进行了数值仿真,并与风洞实验进行了对比。分析了不同风速、阻流体形状、尺寸以及间距直径比对俘能结构的影响,得出了以下结论:
(1)风速及阻流体形状对涡致振动下的T型悬臂梁压电俘能结构具有明显的影响。其仿真和实验结果均显示,在测试范围内,压电悬臂梁产生的电压均随风速的增大而增大,同一风速下,圆柱形阻流体产生涡致振动的效果最好,其次是四棱柱,最差的是六棱柱。当风速为6.5 m·s-1,阻流体为直径0.02 m,高0.05 m的圆柱时,T型悬臂梁压电俘能结构实验输出电压和功率最大分别为1.02 V和1.04 μW。
(2)圆柱形阻流体的尺寸参数对T型悬臂梁压电俘能结构的电压及能量转化具有明显的影响。相同风速下,阻流体直径为0.02 m时,产生的电压大于阻流体直径为0.03 m和0.01 m时,而阻流体直径为0.03 m时又略大于阻流体直径为0.01 m时。当风速为6.5 m·s-1时,阻流体直径为0.01、0.02、0.03 m时的实验输出功率分别为0.29、1.04、0.74 μW。
(3)阻流体与T型悬臂梁压电俘能结构的间距直径比对电压有着较大的影响,电压随间距直径比的增大,先增大再减小而后不变,当间距直径比为2时,T型悬臂梁产生的电压最大,即最佳间距直径比为2。
以上研究结果可以为实际研制风中涡致振动能量收集结构提供参考,也为微型传感器等低功耗产品持续稳定供能的问题提供了一种解决方案。

