用于气象探测的阵列式球型温度传感器设计

丁 枫，刘清惓，杨 杰 ，陈高颖， 袁 宇，付川琪

(1.南京信息工程大学江苏省气象探测与信息处理重点实验室，江苏南京 210044；2.南京信息工程大学大气环境与装备技术协同创新中心，江苏南京 210044；3.江苏省气象传感网技术工程中心，江苏南京 210044)

0 引言

当太阳光线照射到温度传感器表面时，通过辐射吸收及热传导的方式造成的温升将叠加在传感器所测的环境温度上，由此造成的测量误差被称为太阳辐射误差[1]。目前常用的传感器存在辐射误差，E. Erell等[2]通过理论分析和实验证明了太阳辐射误差与太阳辐射强度成正相关，而与气流速度负相关。因此，要利用防辐射温度传感器来减弱太阳辐射带来的影响。根据不同的热交换方式，防辐射温度传感器分为自然通风与强制通风。R. Nakamura等[3]通过实验研究发现，不同型号的防辐射温度传感器在不同环境参数下的辐射误差呈现差异，例如，USCRN(U. S. climate reference network)与MMTS(maximum and minimum temperature system)相比，夜间差异在0.2～0.4 K，白天的差异则多达1.0 K[4]。日本学者研究发现百叶箱的误差和风速、太阳方向角等环境因素相关，引起的误差约为1 K，还有学者发现误差更大的实验结果。因此，目前常用温度传感器难以满足气象观测日益提高的精度要求。

为提高地表气温观测精度，本文提出一种低辐射误差的阵列式球形温度传感器，且无需安装于百叶箱或防辐射罩内，利用计算空气动力学(CFD)方法计算出传感器相互之间的辐射误差比值，并采用极限学习机(ELM)算法获得该比值与各环境因素的关系，为了验证阵列式球形温度传感器的观测精度，开展基于标准气温测量实验的太阳模拟平台数据测量实验。

1 阵列式球形温度传感器设计

1.1 传感器工作原理

阵列式球型传感器包含3个具有不同反射率涂层的温度传感器探头。在同一环境下，3个探头的辐射误差不同，均与太阳辐射强度、环境风速、下垫面反射率等环境因素有关。因此只需量化不同探头之间的辐射误差比值与各环境因素的关系，即可推导出真实环境温度，传感器结构如图1所示。

图1 原理示意图

实验中，传感器探头A表面涂覆一层反射率约0.2的黑色涂层。探头B表面无涂层，铜球反射率约0.5。探头C表面涂覆一层反射率约0.2的白色涂层。无辐射环境下，3个探头的温度测量值均为Tx。当施加一定强度太阳辐射后，温度传感器A的温度为Ta，辐射误差为ΔTa；温度传感器B的温度为Tb，辐射误差为ΔTb；温度传感器C的温度为Tc，辐射误差为ΔTc。此时传感器探头之间的辐射误差比值：

(1)

(2)

η(P,ν)，λ(P,ν)为关于P，ν的特定函数，P为太阳辐射强度，ν为风速。由此可推算出等式：

(3)

(4)

由上述计算等式变化可推算出大气温度真实值Tx：

(5)

(6)

(7)

将求得Tx1与Tx2的平均值作为真实环境温度最终值Tx，其中式(5)与式(6)为辐射误差比值换算公式。

1.2 传感器及测量电路设计

本文设计了一种通过辐射误差比值反推环境温度真实值的阵列式球形温度传感器。利用空心铜球作为外壳，采用Pt100铂电阻作为测温探头，并通过硅酮导热胶使铜球与铂电阻贴合。根据黑色、白色与原色3种涂层使球形温度传感器具有不同的太阳辐射吸收率，并通过支撑片每2.5 cm固定一种球型温度传感器探头。阵列式球形温度传感器结构图如图2所示。

图2 阵列式球形温度传感器结构图

高精度测温电路由STM32F103C8T6处理器、阵列式传感器数据采集系统和串口传输系统组成，将阵列式球形温度传感器采集的数据经过串口发送到上位机显示与分析，具体设计框图如图3所示。

图3 温度测量电路系统设计框图

本设计温度采集系统中的传感器探头采用4线制接法[5]，运用比率法消除引线误差，提高测量精度[6]。利用Isotech的镓熔点室和水三相点室进行铂电阻标定实验，并利用Fluke1595A测量电桥对真实温度进行记录，该测温电桥仪器具有较好的稳定性和准确性，电压噪声达到3 nV级别。

2 计算流体动力学仿真分析

2.1 传感器物理模型建立

本文使用三维实体建模软件Pro/E建立阵列式球型温度传感器的物理模型。空心铜球的直径、内壁直径、开孔直径分别为6 mm、5.5 mm、3 mm，将3个不同吸收率的传感器小球，间隔6 mm放置，确保区域环境的一致性，传感器基本材料参数见表1。

园林花卉养护与管理，直接影响园林工程整体质量与综合效益，故此管理人员一定要给予其一定重视，并编制相关的质量管理标准。结合园林花卉工程具体养护管理项目，依照相关标准进行质量检验，将基础性养护设为始发点，实现对园林花卉养护管理工作质量的有效管控。

表1 传感器基本材料参数

然后，使用软件ICEM对传感器几何模型进行网格划分，利用长方体空气域包裹3个温度传感器的方式，建立整个仿真模型。为满足仿真的收敛性和准确性的要求，将长方形空气域设置为120 mm×120 mm×360 mm，并分别将正方形面设置为速度入口与压力出口，传感器及空气域网格。经系统分析，该模型的网格质量大于0.35，网格质量基本满足FLUENT仿真要求[7]。

2.2 流固耦合数值计算

本文采用CFD方法对传感器进行仿真分析，首先利用热流密度表示太阳辐射强度，其次采用能量方程计算辐射传热、对流换热，并选用k-e模型和压力与速度进行SIMPLE算法。针对动量、能量的求解，可以先选定一阶迎风格式，再采用二阶迎风方式。对于设置模型边界条件，选择空气域的进风口为速度入口，出口为压力出口，空气域四周设置为滑移壁面，并将3个球型传感器设置不同的表面吸收率，白色涂层设置为20%，原色涂层为50%，黑色涂层为80%。为模拟真实实验环境的需求，本文设置不同的太阳辐射强度和风速进行仿真研究。

当太阳辐射强度为1 000 W/m2，风速为3 m/s时，阵列式球形传感器的温度场分布如图4所示。上、中、下层分别为黑色涂层、原色涂层和白色涂层，在辐射与热对流的影响下，误差升温分别为：1.67 K、1.37 K、1.04 K。

图4 传感器温度场分布图

2.3 仿真结果分析与研究

本文通过计算流体动力学仿真的方法，对不同风速和太阳辐射强度下的阵列式球形温度传感器进行辐射误差比值分析。太阳辐射强度为100～1 050 W/m2，步长为50 W/m2；风速变化范围为1～5 m/s，步长为1 m/s，黑色涂层传感器探头与原色涂层传感器探头温差比值记为ΔTa/ΔTb；原色涂层传感器探头与白色涂层传感器探头温差比值记为ΔTb/ΔTc，仿真数据结果如图5所示。

(a)黑色与原色涂层仿真数据结果

(b)原色与白色涂层仿真数据结果图5 仿真数据结果表

由上述可知，黑色涂层传感器探头与原色涂层传感器探头温差比值ΔTa/ΔTb在2.8上下区间浮动时，数值较为稳定，但部分区间有较为明显的波动，在风速为2 m/s，太阳辐射强度为500 W/m2时，数值波动达到最大，波动值为0.059 5；原色涂层传感器探头与白色涂层传感器探头温差比值ΔTb/ΔTc在1.6上下区间浮动，整体趋势与ΔTa/ΔTb相同。在风速为5 m/s，太阳辐射强度为100 W/m2时，数值波动较大，波动值达到0.023 5。因此对于阵列式球形温度传感器中的辐射温差比值，并不能单一的认为是一个常数，而是与环境因素相关的多元非线性函数。

2.4 辐射误差比值计算

为解决温度传感器温差比值波动问题以及CFD仿真仅能计算分析离散模型的问题，本文采用极限学习机(ELM)方法[8]，使用前馈型神经网络，获得不同太阳辐射强度与风速下的温差比值误差订正方程。利用CFD仿真得到的数据作为极限学习机神经网络的训练组，将激活函数设定为sigmoid函数，通过计算输出矩阵的广义逆矩阵，通过最小二乘法取得连接权值，最终得出数学模型。本文将风速与太阳辐射强度作为输入变量，阵列式球形温度传感器各测温探头之间的温差比ΔTa/ΔTb、ΔTb/ΔTc作为2个输出变量，分析得出辐射误差修正方程的数学模型。采用ELM算法拟合生成的CFD仿真值与修正模型计算值的对比图和误差图如图6和图7所示。

(a)ΔTa/ΔTb仿真值与计算值对比图

(b)ΔTa/ΔTb仿真值与计算值误差图图6 黑色与原色涂层修正模型结果

根据误差对比图可知，修正比值与仿真比值之间的均方根误差为0.024 5 K，故该算法的回归拟合精度良好。输入环境因素中的太阳辐射强度数据与风速数值，可计算出球形温度传感器的温差比值，并通过换算公式得到环境真实温度值，进一步提高了阵列式球形温度传感器测量的准确性。

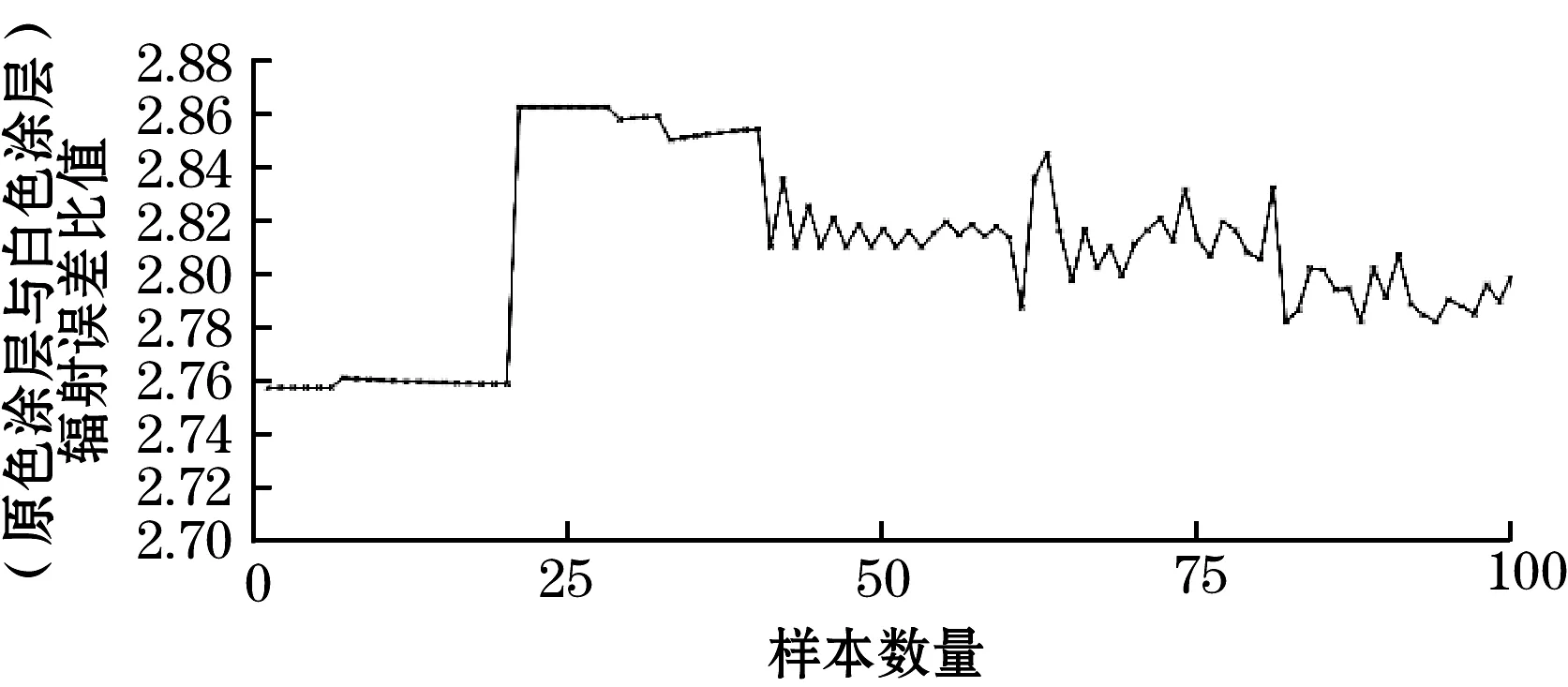
(a)ΔTb/ΔTc仿真值与计算值对比图

(b)ΔTb/ΔTc仿真值与计算值误差图图7 原色与白色涂层修正模型结果

3 实验测试及分析

3.1 实验平台搭建

实验过程中，利用低气压风洞与太阳模拟器搭建本实验观测平台，将阵列式球形传感器放置在低气压风洞中心处，保证区域环境的一致性与稳定性。该低气压风洞包括2台双极旋片式气泵、1根石英玻璃管和2个气压检测仪，利用Fluke1595A测温电桥测得的标准数据作为对照组，该测温电桥的测量准确度在典型的测温学比例(0.25～4.0)范围内，太阳模拟器采用全光谱射线模拟系统，系统内部的球形短弧氙灯具有匹配度极佳的光谱，且输出功率大、亮度高[9]，最大可模拟1 000 W/m2的辐射强度。使用CMP-10的测量结果作为辐射强度标准，确保实验的真实性与可靠性，实验平台现场图片如图8所示。

图8 太阳模拟实验平台

3.2 实验验证及数据分析

由表2可知，阵列式球型温度传感器中黑色涂层与原色涂层的辐射误差比值ΔTa/ΔTb修正值与实验差值的平均值为0.042；原涂层与白色涂层的辐射误差比值ΔTb/ΔTc修正值与实验差值的平均值为0.053。通过辐射误差比值换算公式计算出当前环境真实温度，与测温电桥测得标准环境温度值进行对比，对照表如表3所示，该传感器温度误差的平均值为0.145 ℃，均方根误差为0.16 ℃。

表2 辐射误差比值修正值与实验值对照表

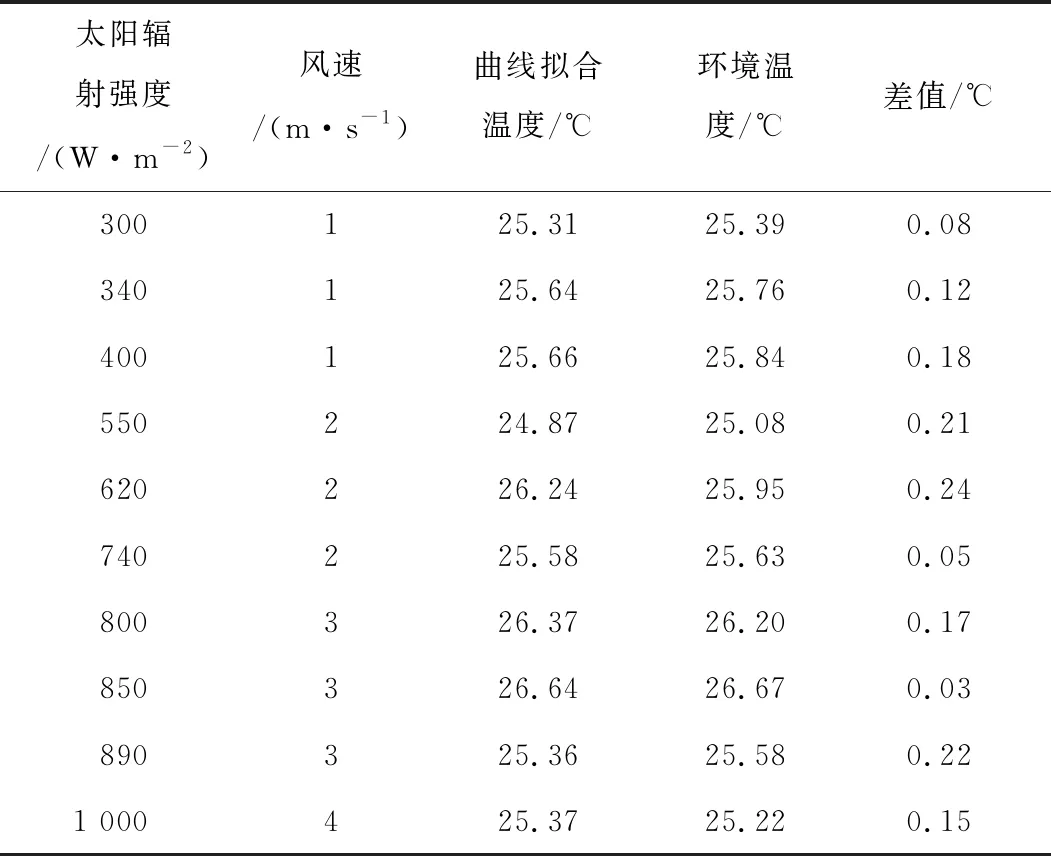
表3 计算温度与测量温度对照表

4 结论

为降低太阳辐射对温度传感器的辐射升温影响，本文设计了一种阵列式球形温度传感器，通过辐射误差比值，计算得出环境真实温度。采用计算流体动力学方法对该传感器在不同太阳辐射强度与风速条件下进行仿真计算，得出辐射误差比值，然后采用极限学习机方法对数据进行拟合处理，最后搭建太阳模拟实验平台对仿真比值进行实验验证分析，得出以下结论：

(1)阵列式球形温度传感器的辐射误差比值是一条波动幅度较小的曲线，风速与太阳辐射强度对辐射误差比值影响较小，但无法忽视环境因素对辐射误差比值的影响。

(2)阵列式球形温度传感器的辐射误差修正比值与仿真值比值之间的均方根误差为0.024 5 K，说明该算法拟合效果良好，提高了阵列式球型温度传感器的测量精度。

(3)阵列式球形温度传感器的温度测量误差均值为0.145 K，均方根误差为0.16 K，具有良好的测量精度，并符合大气科学研究对地表低温观测的精度要求。

本文设计的阵列式球形温度传感器具有较好的测量精度，但未考虑海拔高度和散射辐射等因素的影响，在后续研究中会进一步完善传感器设计和CFD模型，使其精度量级达到更高。