附加质量对力传感器的动态性能影响研究

张 灿

(上海交通大学机械与动力工程学院，上海 200030)

0 引言

除了碰撞等仅有动态载荷的应用，大部分力传感器的应用中需要使用连接机构如转接工装等完成安装，保证力的传递路径通过力传感器，减少或者消除力的分流以保证测量精度。但是在实际操作中这些额外的工装等作为附加质量会对传感器的动态性能带来影响。尤其对于刚度低、质量小、量程小的力传感器而言，大于传感器本体质量的附加质量增加会造成传感器使用频率的急剧下降，影响动态表现。因此研究附加质量对传感器动态性能的影响，对于工程应用中选择合适的力传感器和配套工装，以保证足够的测量带宽，获取完整动态信号有重要意义。

在实际应用中许多学者已经进行了相应的研究。J. Vanwalleghem[1]等在进行杆式应变力传感器标定时发现，改变实验边界条件如负载质量会对力传感器的动态特性产生影响；E. Korkmaz[2]在切削力应用中观察到了工装质量增加会造成测力台固有频率下降。顾宝栋[3]等把力传感器增加附加质量后因标定频率下降而导致的谐振现象作为“质量增加”来处理；许平[4]等在碰撞试验中利用位移测量研究附加质量对测力墙固有频率影响。总结来看，这些研究并未对附加质量与传感器的动态性能之间的定量关系进行深入探讨，也未对作用机理展开研究。

在较为系统的研究中，查富圆[5]、杨睿[6]的研究系统采用阶跃卸载的方式，研究应变式传感器在5种不同附加质量下的多阶固有频率变化，但所采用的动态标定“加载头”的自身质量过大导致标定出现低附加质量研究的盲区；PTB(德国联邦物理技术研究院，physikalisch-technische bundesanstalt)的M. Kobusch[7-8]和R. Kumme[9]等，日本国家计量科学研究院的Y. Fujii[10-11]等在力传感器动态标定装置中采用了水平碰撞的方式，观测到了附加质量对传感器动态性能的影响并进行了理论猜想，但是并未在研究中进行进一步实验验证。

本文从二阶系统基础理论出发，由力传感器传递函数展开后获得的幅频特性函数为基础，对传感器动态特性受附加质量的影响进行理论分析。随后采用落锤法对传感器动态性能和附加质量之间的理论关系进行实验验证。最后在实验中调整冲击参数，观察不同边界条件下实验结果的差异。实验证明了附加质量对传感器动态性能影响理论的有效性。

1 力传感器的模型及其动态性能指标

1.1 力传感器模型建立

由于在力传感器的工程使用中多采用单端固定在基座或地面等刚性面的结构形式，力传感器的动态表现可以被简化为如图1所示的一个简单的弹簧-阻尼-质量块系统，这其中k为传感器的刚度，m为传感器上部预紧结构的质量，c为等效阻尼。

图1 力传感器与简化的弹簧-阻尼-质量块模型

实际应用中，附加质量一般是指除了上台面以外的工具、执行器、工装等二次负载，与预紧组件相比这些结构件质量更大，刚度更低，结构更复杂。因此在实际使用中就必须考虑二次负载的结构参数对已有传感器力学模型的影响。

1.2 力传感器的传递函数与幅频特性

假设预紧结构与传感器的连接，传感器与安装基座的连接均为刚性，则力传感器在外力x(t)的作用下，上部预紧结构会产生一个y(t)的位移，其系统平衡状态下的微分方程为[12]

(1)

对式(1)进行拉氏变换后，可得

(2)

将s=jω代入式(2)中，即可得到传感器的幅频特性的表达式：

(3)

通过力传感器的幅频特性表达式，可以获得力传感器对不同频率输入信号的输出响应，并得到幅频特性图，这对研究力传感器的可用频带范围、阶跃信号响应、超调量预测等有重要意义。

1.3 力传感器的固有频率与附加质量的理论关系

力传感器的动态性能指标可以分为时域指标和频域指标。由于频域指标均为时域指标经过快速傅里叶变换取得，因此时域和频域指标之间可以进行相互换算。在实际应用中一般以力传感器的频域指标作为传感器动态性能衡量的标准。根据式(3)可以得到传感器的幅频特性图，如图2所示。

学生作为教学中的接受方，具有一定的差异性，在应用混合式教学的过程中，我们要尊重学生的个性，了解学生的共性，从而选择合适的混合教学方式。首先，教师要重视学生的个性色彩，根据学生的基础情况，选择相应的知识灌输；另外，学生划分多个学习小组，基础相当的学生分到一个小组，根据小组自身学习的需要制定小组内部的学习的方式、内容和数量，充分发挥了学生的学习自主权。最后，不管是什么教学模式都要实现英语学习小组之间的沟通交流，主动参与网上互动，与教师在线互动，及时解决英语难题。所以，在实际的工作中我们不能不切实际脱离生活，英语教育内容应与日常生活息息相关，这样的混合式教学活动才能得到想要的效果。

图2 力传感器的幅频特性图

其中固有频率fn由角频率ωn转换而来：

(4)

图2中，力传感器的动态指标包含固有频率、使用频率范围、频率下限等，其中固有频率fn是描述力传感器动态测量性能的最重要参数，该参数会直接影响传感器的可用频带范围，并且会影响时域指标中的上升时间指标，可以直接用于衡量力传感器对阶跃信号的响应能力。

由式(4)可得，传感器的固有频率主要受到结构刚度和质量的影响。由于力传感器附加质量的结构一般为金属结构件，连接一般采用螺栓安装，故在此可以假设附加质量不会影响原有传感器测量结构的刚度。而附加质量的增加在传感器的安装中基本不可避免，因此该附加质量m′的影响可表述如下：

(5)

由式(5)可以看出当传感器本身质量m较小，而附加质量m′较大时，传感器的固有频率会出现急剧的下降。当附加质量m′=3m时，传感器的固有频率会变成原有固有频率的一半；而当附加质量m′=15m时，传感器的固有频率会变成原固有频率的1/4。

在动态测试中，如何预测被测信号的频率范围，并且准确的设计相应的力传感器及附加结构进行测量是最大的难点。通过式(5)，可以在进行测试之前通过对结构信息的收集，估算出被测信号的频率范围；通过附加结构质量、刚度信息与传感器参数的计算，可以获得力传感器频率响应范围的变化，保证测量的准确。

2 实验及分析

2.1 实验传感器选择

选取9371A，9321A及4576A等3款力传感器，如图3所示，这3款力传感器中前2种为压电式力传感器，第三种为应变式力传感器。压电式力传感器刚度高，具有高的固有频率，更适合动态测量；而应变式传感器则因刚度较低，只适合测量静态及准静态事件。选取不同技术的力传感器也可以验证式(5)的普遍有效性。

(a)9321A (b)9371A (c)4576A图3 压电式力传感器9321A，9371A及应变式传感器4576A

3种传感器在量程、刚度、预紧形式、结构形式、质量上均有差别，因此传感器的固有频率也有较大差异。通过对传感器附加结构质量的称重，在假设附加结构不影响原有传感器刚度的前提下，利用式(5)对附加质量后的固有频率进行预估如表1所示。

表1 9371A，9321A，4576A传感器参数对比及固有频率预测

2.2 实验设置

与传统的落锤实验是为了获取被校验传感器的时域信号并进行波形对比不同，本次的落锤实验是希望通过使用硬塑料锤头对加装附加质量后的力传感器进行冲击激励，以激发力传感器与附加结构的固有频率。考虑到该实验中硬塑料锤头的刚度低，初速度小，因此在冲击过程中产生的信号带宽应在10 kHz以内。再结合表1的传感器相关信息可知，应变传感器4576A会在冲击激励作用下出现共振状态，而压电传感器9371A与9321A则不应当出现共振。

利用头部为半圆形的、质量为50 g的硬质塑料锤头在50 cm处的自由落体运动作为落锤冲击的激励源，如图4所示。半圆形的塑料锤头可以保证在冲击过程中力传感器与锤头的点接触，防止出现剪切力干扰；外部的透明玻璃管主要起到导向作用，保证锤头施力在力传感器的有效范围内；同时在底板上有固定力传感器的卡槽，防止力传感器在受冲击过程中产生横向位移；为保证每次落振高度的一致性，多次试验中均使用锤头末端与玻璃管上表面齐平的初始落振位置，以方便定位；经过多次试验比对，证明实验结果重复性高，可复现性强。

图4 落锤标定装置及放大器、示波器

信号的采集和分析采用了KiDAQ动态数据采集仪，应变信号的采集采用5501A动态电桥采集板卡，压电信号的采集使用了5509A电荷电压自适应采集卡，采样频率为100 kSPS。同时使用了设备的Pre-trigger功能，设定数据阈值后采用软件触发，防止了人手工可能带来的误操作。数据后处理和分析采用了Jbeam软件。具体系统结构如图5所示。

图5 数据测试、采集、分析系统结构图

2.3 实验结果分析

2.3.1 落锤实验时域信号分析

经过多次落锤实验以后得到多组实验结果，虽然冲击事件有一定的随机性，但是由于在实验定义中和落锤结构设计中均考虑并限制了会带来不确定的因素，如碰撞接触面、初速度、偏载等，在对最后15次落锤测试结果进行的整理后表明，幅值数据的重复性在10%以内。为了保证信号分析的代表性，随机选取其中一组实验数据进行分析，如图6所示。

对时域信号进行分析，得出如下结论：

(1)应变式力传感器4576A与小量程压电式力传感器9321A均在落锤试验中出现了明显的共振，其中4576A的单个振荡周期较长，而9321A的单个振荡周期较短。与此同时9371A未出现明显的信号振荡及失真。

(2)共振后4576A的调节时间接近50 ms，而9321A的调节时间约为25 ms，由于调节时间是传感器固有频率和阻尼比系数的综合反映，这里无法通过调节时间对比直接得到固有频率关系。

(3)3个测量结果的峰值差异较大，其中4576A的峰值为611.36 N，9371A的峰值为1075.86N，9321A峰值为1609.14N。初步推测应变式力传感器4576A阻尼系数较大，因此共振幅值较小，且应变式传感器共振频率较低，无法测量反共振峰以外的信号分布，因而信号要远小于同样出现共振的9321A。

(4)与9321A，4576A相比，9371A传感器并未出现明显的负值，这是由于硬塑料锤头冲击频谱无法达到9371A谐振范围内，未引起9371A传感器共振。

在经过上述分析后，将落锤测试高度降低至20 cm，在冲击信号带宽明显下降的情况下，4576A的输出最大，而9321A仅出现了轻微的共振，证明了对于结论(3)的分析是正确的。

(a)9371A落锤测试

(b)4576A落锤测试

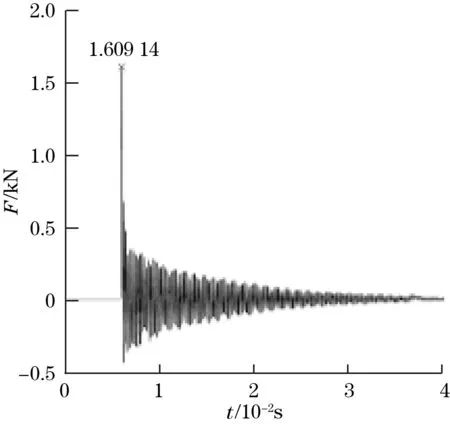
(c)9321A落锤测试

2.3.2 落锤实验频谱分析

在频谱分析中考虑到传感器固有频率差异巨大，因此将3个传感器分别在不同的频率范围内进行分析。

如图7所示，对9371A传感器的频谱分析结果可以得到，该传感器结构虽然有附加质量，但是附加质量对传感器整体固有频率结构的影响有限，加上硬塑料锤头的激励频带宽度较窄，该传感器并未出现明显的共振。

图7 9371A落锤测试结果频谱分析

如图8所示，对4576A传感器测试结果的分析可知，由于附加质量增加，传感器的固有频率由2 kHz下降为1.5 kHz，与表1中的预测相符。

图8 4576A落锤测试结果频谱分析

如图9所示，从9321A传感器的频谱分析结果可以看出，力传感器的固有频率从原有的55 kHz降低到了5.3 kHz，与表1的预测不符。由式(5)可知，传感器固有频率不仅与附加质量有关，也与结构刚度k有关。9321A传感器的附加结构为伞形结构，当落锤的作用点不在力传感器本体安装范围内时，由于缺少支撑而带来的较低结构刚度k就成为了影响传感器固有频率的主导因素。

图9 9321A落锤测试结果频谱分析

3 结论

本文通过对力传感器等效二阶系统在平衡状态下的微分方程进行拉氏变换得到了力传感器的传递函数，继而通过传感器传递函数获得了传感器的幅频特性，基于传感器的幅频特性曲线提出了附加质量对传感器动态性能影响的理论计算方法，并通过实验验证了该方法的有效性。

本文在实验中未考虑如下问题：(1)结构刚度变化对传感器动态性能影响，以及结构刚度变化与质量增加同时作用下的传感器动态性能的改变；(2)冲击变载荷对传感器动态性能的影响，也是本次的理论计算与实验结果的误差来源；(3)安装面阻尼特性对传感器动态性能的影响。