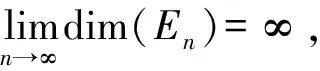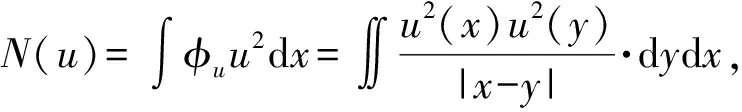一类非齐次Schrödinger- Poisson系统解的存在性
蔡武晋 边 慎 赵雷嘎
(1.北京化工大学 数理学院, 北京 100029; 2.北京工商大学 数学与统计学院, 北京 100048)
引 言
本文研究非齐次Schrödinger- Poisson系统
(1)
式中V(x)和φ(x)分别表示有效势和电势。系统(1)首先在文献[1]中被提出,用于描述三维空间中与静电场相互作用的非线性Schrödinger方程的驻波,f(u)用于模拟多个粒子间的相互作用,g(x)为非齐次扰动。
近年来,在对非线性项和位势条件进行的各种假设下,系统(1)受到广泛研究[2-10]。文献[2]、[4]的研究表明,f(u)关于u的增长阶p的范围会对泛函的紧性和解的存在性产生影响。
当位势函数为常数时,Ruiz[4]研究了带有参数的一类自治Schrödinger- Poisson方程
式中,λ>0,2 本文对一般的非线性项f(u)以及位势函数V(x),研究系统(1)解的存在性和多解性。特别地,允许f(u)的增长性包含3 设势函数V(x)∈C(R3,R)满足: (V1)V(x)=V(|x|); 其中(·,·)表示R3的内积。 设g(x)∈C1(R3,R)∩L2(R3,R)为非负函数,满足: (g1)g(x)=g(|x|)≢0; 这里(V1)和(g1)为函数满足径向对称的条件。 对非线性项f(u)∈C(R,R),设 (f1)f(0)=f′(0)=0; (f2) ∃C>0,使得|f(u)|≤C(|u|+|u|p), ∀u∈R,其中p∈(2,5); 本文的主要结果是如下定理。 定理1设(V1)~(V3)、(f1)~(f3)和(g1)~(g2)成立,则存在Cp>0,当‖g‖2 进一步对非线性项f(u),设 (f4)f(-u)=-f(u),∀u∈R; (f5) ∃θ>4,使得0≤θF(u)≤uf(u),∀u∈R。 定理2设(V4)、(f1)~(f2)和(f4)~(f5)成立,则对任意的g(x)∈L2(R3),系统(1)在HV×D中存在无穷多解。 本文利用变分法进行证明。由于p的范围会对泛函的几何结构和紧性条件产生影响,当3 首先将系统(1)转化为单个方程[4]。对任意的u∈H1(R3),可得到方程-Δφ=u2在空间D1,2(R3)中的唯一解φu,此解可表示为 将φu带入到系统(1)的第一个方程,得 -Δu+V(x)u+φu(x)u=f(u)+g(x) 于是定义变分泛函为I:H→R (2) 根据文献[1]中的命题4,易证I∈C1(E,R)和(u,φ)∈H×D是方程(1)的解当且仅当u∈H是I的临界点,且φ=φu。引理1收集了φu的一些性质[4]。 引理1 (Ⅰ)对任意的u∈H,φu(x)≥0,x∈R3; (Ⅲ)对t>0,有φvt(x)=t2φv(tx),其中vt(x)=t2v(tx); (Ⅳ)若在H中un⇀u,则在D中φun→φu。 定理1的证明分为两步:一是通过Ekeland’s变分原理证明其负能量解存在;二是通过结合单调性方法的山路定理证明其正能量解存在。 由(f1)~(f2)知,对任意ε>0,存在Cε>C,使得 |f(u)|<ε|u|+Cε|u|p (3) 由(f3)知,存在C>0,使得 F(u)≥C|u|θ,θ>3 (4) 引理2设(f1)~(f2)成立,则存在Cp>0,t0>0和ρ0>0,使得当‖g‖2 证明由式(3)可知 式中S为H嵌入到Lp(R3)的最佳Sobolev常数,故对任意的u∈H,有 令A(t)=t/4-Ctp/[(p+1)Sp+1],t≥0,则A(t)在[0,+∞)存在最大值。 当‖g‖2 引理3设(f3)和(g1)成立,令c0=inf{I(u):u∈Bt0},其中Bt0={u∈H:‖u‖≤t0},则c0<0,且存在u0∈H,使得I(u0)=c0。 由Ekeland’s变分原理易得序列{un}⊂Bt0满足 (Ⅰ)I(un)→c0; (Ⅱ)I′(un)→0,在H-1中(H-1为H的对偶空间)。 因为{un}⊂Bt0,显然有界,则{un}是泛函I的一列有界(P.S)序列。 由H嵌入到Lp(2 易知F(u)的增长性在(3,6)之间,当θ∈(4,6)时容易证明泛函(P.S)序列的有界性,但在θ∈(3,4)时难以证明(P.S)序列是有界的,所以我们引用如下单调性方法来构造θ∈(3,4)时的泛函的特殊(P.S)序列。 命题1(L.Jeanjean’s引理[12]) 假设(H,‖·‖)为Banach空间,J∈R+是一个区间, (Φμ)μ∈J是定义在空间H上的一列C1泛函并且有如下形式 Φμ(u)=A(u)-μB(u),∀μ∈J 式中,B(u)≥0,∀u∈H。当‖u‖→∞时,B(u)→+∞或者A(u)→+∞。如果存在v1、v2∈H,使得对任意的μ∈J,有 式中,Γ={γ∈C([0,1],H):γ(0)=v1,γ(1)=v2}则对几乎处处的μ∈J,存在序列{vn}⊂H满足: (Ⅰ){vn}是有界的; (Ⅱ)Φμ(vn)→c(μ); (Ⅲ)在H的对偶空间中Φ′μ(vn)→0。 为应用命题1寻找系统(1)的正能量解,构造近似问题 引理4设(g1)成立,则 (Ⅰ)存在ρ0、t0>0和满足‖e‖>t0的函数e∈H使得对任意的‖u‖=t0,Φμ(u)≥ρ0成立;Φμ(e)<0,其中μ∈[1/2,1]; (Ⅱ)对任意的μ∈[1/2,1],有 式中Γ={γ∈C([0,1],H):γ(0)=0,γ(1)=e}。 证明 注意到θ>3,存在与μ∈[1/2,1]无关且充分大的常数t0>0,使得Φμ(wt0)<0对μ∈[1/2,1]一致成立。所以取e=wt0,(Ⅰ)得证。 (Ⅱ)由cμ的定义可知,对μ∈[1/2,1]有cμ≥c1≥ρ0>0,其中ρ0>0由(Ⅰ)给定,既然Φμ(0)=0且Φμ(e)<0对μ∈[1/2,1]一致成立,则(Ⅱ)得证。证毕。 0<ρ0≤Φμk(uk)=cμk≤c1/2 (5) 对任意的k∈N,有 Φ′μk(uk)=0 (6) 在定理1的假设条件中,仿照文献[13]的方法,可以证明uk满足下列Pohozaev恒等式 下面证明序列{uk}的有界性,有如下引理。 引理5在定理1的条件下,{uk}在H中有界。 证明将证明分为两步。 步骤1 证明{‖uk‖2}有界。 这里ο(1)表示k→+∞时的无穷小量。解上述方程组可得 Bk=4(3Dk-Ek)+ο(1) 结合(f3),由于θ>3,则当k充分大时Bk<0,此时与(V3)矛盾,所以{‖uk‖2}有界。 定理1的证明由引理3知,u0为系统(1)的负能量解;由引理5和μk→1易知,{uk}是I=Φ1的有界(P.S)序列,再由H紧嵌入到Lp(2 本节中,定义变分泛函为IV:HV→R。 为证明定理2,给出如下定义。 定义1((P.S)c条件) 设I∈C1(E,R),其中E是Hilbert空间。如果一序列{un}⊂E满足I(un)→c且I′(un)→0,则称序列{un}在水平c上是一(P.S)序列,记为(P.S)c序列。如果任何(P.S)c序列包含一个收敛子序列,则称I满足(P.S)c条件。 定义2((sP.S)c条件[11]) 设I∈C1(E,R),E是一Hilbert空间,I满足(P.S)c条件。若序列{un}⊂E满足: (Ⅱ)存在实数λn,使得 则称序列{un}在水平c上是一对称(P.S)c序列,记为(sP.S)c序列。如果任何(sP.S)c序列在E中包含一收敛子序列,则称I满足(sP.S)c条件。 命题2(对称山路引理[11])I是一C1泛函,在Hilbert空间HV=X⊕Y上满足(sP.S)c条件且dim(X)<∞,设I(0)=0且满足: (Ⅰ)存在ρ>0和α≥0使得infI(Sp(Y))≥α; 则I具有一趋于无穷的临界值序列。 定理2的证明将分为下面3个引理。 引理6设(V4)和(f4)成立,则泛函IV满足(sP.S)c条件。 证明先证IV对任意的c满足(P.S)c条件。设{un}为一(P.S)c序列,结合(f5)则有 (7) 故‖un‖有界,再由(f4)、引理1与Hölder不等式易知 N(un)→N(u),〈N′(un),v〉→〈N′(u),v〉,∀v∈HV 结合Nemytski算子的连续性[14]易推导出{un}的强收敛性。证毕。 由HV嵌入到L2的紧性,特征值问题 具有一趋于无穷的特征值序列,记为0<λ1≤λ2≤…≤λk≤…,设ek表示特征值为λk时对应的特征函数。 引理7设(f1)~(f2)成立,则对足够大的k0∈N,存在ρ0>0,使得对∀u∈Y:=span{ek;k≥k0},当‖u‖=ρ0时,IV(u)≥1。 证明令A=‖g‖2,因为N(u)≥0,由式(3)再结合Hölder不等式,则对u∈Y有 式中,r=3-θ/2>0。 引理8设(f5)成立,令X=span{ej;j 证明由引理3得 N(u)≤C1‖u‖4 则对u∈En和R>0,由(f5),有 由于θ>4,再由有限维空间范数的等价性,可得结论。证毕。 定理2的证明由引理6~8,可知所有关于命题2的条件满足,所以得到IV具有一趋于无穷大的临界值序列,从而系统(1)具有无穷多解。 至此,定理1和定理2已全部证明。1 定理的提出




2 变分框架及预备引理

3 定理1的证明

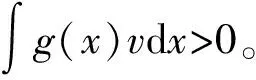

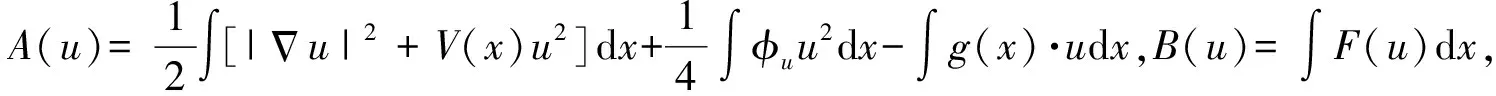




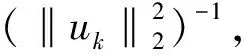



4 定理2的证明